НЕЙТРОННЫЕ МЕТОДЫ ИССЛЕДОВАНИЙ В ФИЗИКЕ КОНДЕНСИРОВАННОГО СОСТОЯНИЯ Лекция

НЕЙТРОННЫЕ МЕТОДЫ ИССЛЕДОВАНИЙ В ФИЗИКЕ КОНДЕНСИРОВАННОГО СОСТОЯНИЯ Лекция 3 Квазичастицы в физике твердого тела В этой лекции будут изложены основные идеи и принципы, положенные в основу теоретического описания свойств кристаллических тел. Квазичастицы и элементарные возбуждения. Методы исследования квазичастиц.

Квазичастицы и элементарные возбуждения Конденсированное состояние вещества – ансамбль частиц (атомов или молекул), имеющий дальний или ближний порядок в расположении частиц, объем которого при заданных внешних условиях определяется силами взаимодействия между частицами. ~1022 частиц в см 3 Это очень и очень много!!! и они сильно-взаимодействующие…

1) Теоретическое описание и объяснение свойств конденсированных сред (твёрдых тел и жидкостей), исходящее из свойств составляющих их частиц (атомов, молекул), представляется делом исключительно трудным , потому что число частиц очень велико (~ 1022 частиц в 1 см 3), и они сильно взаимодействуют между собой. 2) Для понимания свойств твердого тела важна не только (и не столько!) структура, но и динамика (Характер перехода в возбужденное состояние)

Структурные элементы кристалла (атомы или молекулы) сильно взаимодействуют между собой движения частиц в кристалле имеют кооперативный характер возбуждения в кристалле квантованы квант движения - элементарное возбуждение

Полная энергия кристалла может быть представлена в виде: Основное состояние Возбуждения: движения атомов, электронов… Индекс характеризует тип элементарного возбуждения, n - целые числа, показывающие число элементарных возбуждений типа .

О значении исследований динамики…. Полная энергия связи основного состояния отнюдь не является очень важной физической величиной, и для объяснения свойств физической системы дает не слишком много. Что действительно важно, это поведение нижних возбужденных состояний относительно основного - тех состояний, которые можно возбудить относительно низкими температурами или слабыми внешними полями. Мы сразу представляем металл или полупроводник, в том случае, если все поведение системы определяется низколежащими возбужденными состояниями, о которых говорят как о наличие подвижных носителей заряда; или представляем упругие и тепловые свойства твердых тел, которые определяются присутствием небольшого числа возбуждений кристаллической решетки, называемых фононами. Именно поэтому наше внимание так часто сосредоточено на совокупности низколежащих возбужденных состояний системы как наиболее фундаментальной ее характеристике. P. W. Anderson “Concepts in solids” 1997

Понятие о квазичастицах кристалл: совокупность невзаимодействующих элементарных возбуждений идеальный газ: совокупность невзаимодействующих частиц элементарное возбуждение частица идеального газа Элементарные возбуждения в кристалле квазичастицы. Квантовомеханическая аналогия (волны де Бройля для частиц) В кристалле возбуждение одной из частиц (например, поглощение одним из атомов фотона), приводящее из-за взаимодействия (связи) атомов к возбуждению соседних частиц, не остаётся локализованным, а передаётся соседям и распространяется в виде волны возбуждений. Этой волне ставится в соответствие Квазичастица с квазиимпульсом p= ħq и энергией E = ħ (q), (q- волновой вектор, длина волны = 2π/|q|).

КВАЗИЧАСТИЦА— особый долгоживущий многочастичный комплекс, который, в отличие от обычных (структурных) частиц, составляющих систему, слабо взаимодействует со своим окружением. Поэтому К. находится в определенном квантовом состоянии со своей волновой функцией, энергией, импульсом (в случае кристалла — квазиимпульсом), спином и т. д. , двигаясь как целое подобно обычной частице (отсюда термин «К. » ). Будучи коллективным образованием, К. имеет состав, непрерывно обновляющийся при её движении; лишь в предельных случаях этот состав фиксирован как у связанного состояния типа молекулы. Концепция КВАЗИЧАСТИЦЫ, формирование которой связано с именем Л. Д. Ландау (1941— 52), позволила свести сложную динамику системы сильно взаимодействующих частиц к более простой динамике совокупности квазинезависимых объектов. Переход системы из основного в близкое по энергии слабо возбуждённое состояние можно свести к рождению внутри системы некоторого числа квантов возбуждения — КВАЗИЧАСТИЦ Физическая энциклопедия

Основные характеристики квазичастиц: - энергия E = ħω - квазиимпульс p=ħq (определен с точностью до вектора обратной решетки K) - закон дисперсии E(p) , ω(q) (основная динамическая характеристка) -эффективная масса - m*-тензор! (ускорение и действие силы по направлению могут не совпадать, ускрение м. б. против силы (m* <0) – это «дырки» ) - заряд - спин - статистика - энергетический спектр (структура состояний квазичастицы) - функция спектральной плотности состояний d. N/d. E=f(E) - время жизни Ƭ >2π/ω

Сходство частиц и квазичастиц: Квазичастицы могут сталкиваться или взаимодействовать иным образом. При столкновении низкоэнергетических квазичастиц выполняются механические законы сохранения квазиимпульса и энергии. Квазичастицы могут также взаимодействовать и с обычными частицами (например, с фотонами).

Различия частиц и квазичастиц: В отличие от обычных частиц, которые существуют сами по себе, в том числе и в вакууме, квазичастицы не могут существовать вне среды, возбуждениями (колебаниями) которой они и являются. При столкновениях квазичастиц закон сохранения квазиимпульса выполняется с точностью до вектора обратной решетки. Закон дисперсии обычных частиц — это данность, которую нельзя изменить. Закон дисперсии квазичастиц возникает динамически, и потому может иметь самый замысловатый вид и зависеть от внешних условий. Квазичастицы могут иметь дробный электрический заряд.

Основные типы элементарных возбуждений в кристаллах квазичастица комментарий электрон q=-e, s=1/2, 1/m*= 2 E/ p 2 1/me (!) фонон волна упругих колебаний кристалла магнон спиновая волна (волна перемагничивания) полярон электрон+упругая деформация кристалла плазмон коллективная электронная волна (металлы) экситон квазичастица, образованная электроном и дыркой, q=0 (важен для оптических свойств (!) э. Френкеля (локальн. ), э. Ванье-Мотта – бол. рад. )) куперовская пара квазичастица, образованная двумя электронами, s=0 ( «композитное» (!) образование)

Фононы фонон – квант упругих колебаний кристаллической решетки (И. Е. Тамм) Заряд =0 Спин s=0 Статистика Бозе-Эйнштейна Поляризация - определяет тип движения атомов (продольные и поперечные) по отношению к вектору распространения (L+2 T)

Акустические фононы определяют скорость распространения звука в кристалле. При q 0 ω~q. Два поперечных(Т) и одно продольное (L) колебание q Отклонения атомов при малых q в случае поперечного акустического фонона Оптические фононы существуют в кристаллах с более чем одним сортом атомов в элементарной ячейке. При q=0, ω≠ 0. Всего 3 n-3 оптических колебаний. Отклонения атомов q в случае поперечного оптического фонона

Primitiv cell

Фононы в

Магноны (спиновые волны в магнитоупорядоченных структурах) квазичастица, соответствующая элементарному возбуждению системы взаимодействующих спинов, статистика Бозе-Эйнштейна. Предсказал Ф. Блох, 1930 г. Доказательство существования - Б. Брокгауз (1957 г. ) неупругое рассеяние нейтронов на магнонах в ферритах Распространение спиновой волны в линейном ферромагнетике – прецессия атомных спинов.

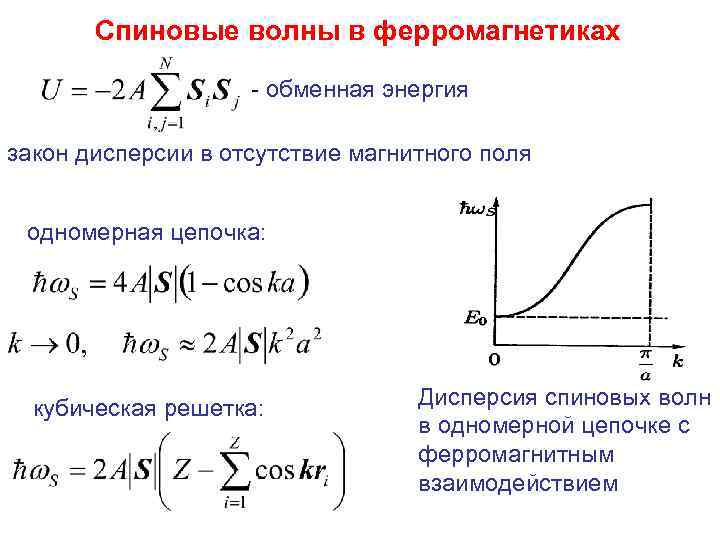Спиновые волны в ферромагнетиках - обменная энергия закон дисперсии в отсутствие магнитного поля одномерная цепочка: кубическая решетка: Дисперсия спиновых волн в одномерной цепочке с ферромагнитным взаимодействием

Дисперсия магнонов в ферромагнетике Fe 3 О 4 (магнетит) q/qmax=2π/a, а – параметр решетки.

Спиновые волны в антиферромагнетиках закон дисперсии для одномерной цепочки в отсутствие магнитного поля В отличие от ферромагнетиков, в антиферромагнетиках при малых k закон дисперсии линеен.

Дисперсия магнонов в антиферромагнетике Rb. Mn. F 3

Ферми-жидкость электронов в металлах , Тяжелые фермионы q = -e s = 1/2 m* = 102 -103 me Перенормировка массы – из-за электрон-электронного взаимодействия Примеры систем: Ce. Al 3, Ce. Cu 2 Si 2, Ce. Cu 6, UPt 3, UBe 13 …

Резюме по квазичастицам 1) Квазичастицы – это идеальный газ. 2) «Электроны» , «тяжелые фермионы» и т. п. – это Фермижидкость. 3) Некоторые свойства Ферми-жидкости можно приближенно описать в рамках концепции Квазичастиц (т. е. уже газа). Учет взаимодействия между фермионами приводит к перенормировке их эффективной массы. При этом часто имеет место терминологическая путаница, когда название “электрон” применяется и по отношению к частицам Ферми-жидкости, и по отношению к частицам Ферми-газа. Между тем эти “электроны” отличаются друг от друга, как и от «настоящего» электрона – свободной частицы в вакууме.

Методы исследования квазичастиц 1) опосредованные: измерение макроскопических параметров (сопротивление, теплоемкость, магнитная восприимчивость) + интерпретация на основе моделей 2) спектроскопические: получение непосредственной информации о структуре спектра и дисперсии квазичастиц

Некоторые спектроскопические методы исследования квазичастиц Метод Измеряемая характеристика неупругое рассеяние нейтронов закон дисперсии фононов и магнонов, спектральная плотность состояний неупругое рассеяние синхротронного излучения закон дисперсии фононов рассеяние и поглощение света энергия оптических фононов (рамановская и ИК спектроскопия ) рентгеновская фотоэмиссионная спектроскопия, микроконтактная спектроскопия, измерение динамической (оптической проводимости) зонная структура ферромагнитный резонанс энергия магнонов вблизи центра зоны Бриллюэна ферроакустический резонанс эффективная масса магнона циклотронный резонанс поверхность Ферми

Общий принцип спектроскопического эксперимента по исследованию квазичастиц E f , kf зондирующая частица после рассеяния E i, k i зондирующая частица (фотон, нейтрон ) до рассеяния K + q = ki – kf ħω = Ei – Ef Объект q - квазиимпульс и ħω - энергия возбужденной (поглощенной) в кристалле квазичастицы Таким образом можно определить закон дисперсии или (при усреднении по поликристаллу и т. п. ) более интегральные характеристики квазичастицы. Чем меньше возмущение объекта при взаимодействии, тем ближе к «истинному» (равновесному) получаемый спектр

Оптические методы Энергия фотона видимого диапазона ~ 1 -2 э. В Закон дисперсии фотона ω=ck (E = 1 e. V ~ 250 THz ~ 1. 2 mkm k ~ 0. 5 10 -3 Å-1) Характерная энергия возбуждений в кристалле~1 -100 мэ. В Характерный волновой вектор ~1 Å-1 При переданной энергии ħω ~1 -100 мэ. В - q~0 (в масштабе ЗБ) Информация об энергии возбуждений только вблизи центра зоны Бриллюэна!!! (Бриллюэновское (акустика) и Рамановское (Мандельштамма –Рамана) (оптика) рассеяние: стоксовские (+ph) и антистоксовские(-ph) линии) Использование СИ позволяет выйти за эти рамки!

Неупругое рассеяние синхротронного излучения Энергия фотонов ~ 10 кэ. В (в 104 раз больше, чем видимый свет!) Переданный импульс может составлять~1 -10 Å-1 при углах рассеяния ~1800. НО! Необходимо разрешение ΔЕ ~10 -7 Ei Можно измерять дисперсию фононов во всей зоне Бриллюэна. Недостаток СИ: нельзя исследовать магноны, проблемы с реализацией столь высокого разрешения.

Неупругое рассеяние тепловых нейтронов Энергия теплового нейтрона ~ 25 мэ. В, ħω= ħ 2 k 2/2 m Переданный импульс может составлять ~ 1 -10 Å-1 и выше Разрешение: ~1 мэ. В (может быть существенно лучше!) Сечения рассеяния на фононах и магнонах сопоставимы Можно измерять дисперсию фононов и магнонов во всей зоне Бриллюэна! Недостатки: большие размеры образцов (~1 см 3), большая длительность эксперимента (5 -10 суток и больше), проблема разделения фононного и магнитного вкладов в экспериментальные спектры.

Что мы узнаём с помощью рассеяния нейтронов. Дифракция нейтронов – как устроено вещество? Подобно рентгенографии дифракция нейтронов дает информацию о кристаллической структуре вещества. При этом возникают дополнительные возможности: - определение магнитных структур; - локализация положения в решетке легких атомов на фоне тяжелых; - структурный анализ сплавов состоящих из атомов с близкими массами; - получение информации об атомной структуре со всего объема образца, а не только из приповерхностного слоя; - возможность контрастировать вклады различных химических элементов с помощью изотопного замещения.

Нейтронная спектроскопия – почему вещество так устроено? Знание закона дисперсии для фононов и его эволюции при изменении внешних условий, дает уникальную количественную информацию о силовом межатомном взаимодействии в кристаллах. Спектральная плотность фононных состояний определяет все термодинамические свойства вещества. Особенности обменного взаимодействия, определяющего корреляцию магнитных моментов в магнетиках, можно исследовать на основе экспериментально измеренного закона дисперсии для магнонов.

Возможности фотонов и нейтронов нейтроны Область волновых векторов возбуждений в конденсированных средах Область характерных энергий возбуждений в конденсированных средах фотоны