Нейтронная физика Лекция 7 Дифракция и нейтронная оптика

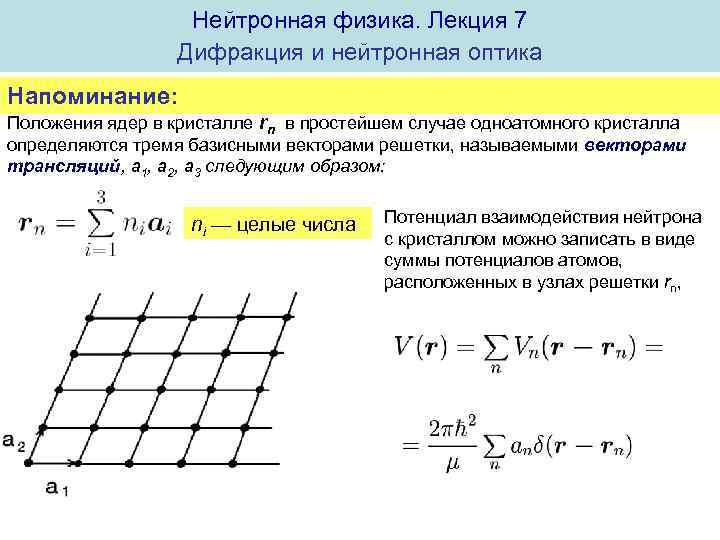Нейтронная физика. Лекция 7 Дифракция и нейтронная оптика Напоминание: Положения ядер в кристалле rn в простейшем случае одноатомного кристалла определяются тремя базисными векторами решетки, называемыми векторами трансляций, a 1, a 2, a 3 следующим образом: ni — целые числа Потенциал взаимодействия нейтрона с кристаллом можно записать в виде суммы потенциалов атомов, расположенных в узлах решетки rn,

В каждой элементарной ячейке может находиться несколько атомов разного типа, которые могут испытывать тепловые колебания в узлах решетки. i будем нумеровать атомы, относящиеся к одной элементарной ячейке, а индексом n — сами элементарные ячейки, то есть координату ra любого атома в кристалле можно представить в виде ra = rn + ri, , где rn = niai, Индексом Для решения дифракционных задач этот потенциал (сумму атомных потенциалов), мы представили в виде суммы потенциалов кристаллографических плоскостей. Последнее называется разложением потенциала по векторам обратной решетки. g – вектор обратной решетки, |g| = 2π/d, где d – межплоскостное расстояние. Характеризует систему плоскостей, перпендикулярных ему

Периодический (в направлении g, ось x) потенциал системы плоскостей можно разложить в ряд Фурье: gn=2 n/d. Можно считать, что каждая гармоника описывает потенциал своей системы плоскостей gn (тогда дифракция n-го порядка это дифракция первого порядка, но на системе плоскостей с межплоскостным расстоянием dn=d/n). Здесь мы учли Поскольку V(r) вещественнен и положили

Мы далее перешли к относительному потенциалу, котрый записали в виде где усредненные по тепловым колебаниям амплитуды гармоник имеют вид структурная амплитуда выглядит следующим образом: Величина e−Wg называется фактором Дебая-Уоллера. Фактор Дебая-Уоллера приводит к резкому уменьшению высших гармоник периодического потенциала кристалла с большими g. Это имеет простой физический смысл. В результате колебаний атомов кристалла их потенциал (даже будучи δ-образным) "размазывается" по области шириной порядка средней амплитуды колебаний ua, а такой потенциал не может передавать импульсы большие, чем ℏg ∼ ℏ/ua.

Нейтронная оптика Если направление падения нейтронной волны таково, что условию Брэгга не удовлетворяет ни одна из систем плоскостей, то нейтрон взаимодействует в основном только с усредненным потенциалом кристалла, т. е. существенна только нулевая гармоника разложения потенциала V 0. В таком (одноволновом) приближении основная система уравнений динамической дифракции сводится к одному уравнению. Условие его разрешимости определяет коэффициент преломления нейтрона в кристалле, который можно связать с амплитудой рассеяния вперед: где Ni — число атомов i-го типа в единице объема. Поскольку такая амплитуда связывает состояния с одинаковым направлением импульса, то естественно, что внутри кристалла распространяется только одна волна с амплитудой u 0.

Итак, пусть из вакуума на кристалл падают нейтроны с импульсом ħke. При пересечении границы изменяется только нормальная составляющая импульса (граница может передавать только нормальный к ней импульс), тогда внутри кристалла волновой вектор нейтрона k 0 можно представить в виде k 0 = ke + Δ· n k 0 Решение и

Проецируя вектор k 0 на n, для нормальной составляющей волнового вектора в кристалле получаем т. е. два решения, отличающиеся знаком. Знак „минус“ соответствует волне, распространяющейся в сторону границы. Это может быть только волна, отраженная от второй границы, если кристалл имеет конечную толщину. Таким образом, общее решение для нейтронной волновой функции внутри кристалла имеет вид Амплитуды c 1 и c 2 определяются из граничных условий. Отражение и преломление в полубесконечном кристалле волновая функция нейтрона в вакууме имеет вид: где r — коэффициент отражения, k’e — волновой вектор отраженной волны, причем, |k’e| = |ke|. Поскольку тангенциальная составляющая импульса сохраняется, а может меняться только его нормальная компонента, то ket = k’et , k’en = −ken

Внутри кристалла условию на бесконечности удовлетворяет только волна, для которой k 0 n > 0, то есть решение с k 0+. Запишем его как Амплитуды отраженнойи преломленнойволн определяются из граничных условий на плоскости nr =0. Представив вектор k 0 в виде k 0 = непрерывности волновой функции на границе получим k 0 t +k 0 n, из Это условие должно выполняться для всех точек r границы, что возможно только при равенстве всех тангенциальных составляющих импульсов (это и есть доказательство этого равенства). Поэтому будем иметь: Аналогично из непрерывности нормальной составляющей градиента (непрерывность тангенциальнойсоставляющейпри этом будет автоматически обеспечена непрерывностью волновой функции и равенством тангенциальных составляющих волновых векторов) следует:

получаем простую систему Откуда для коэффициента отражения r и величины |c|2 будем иметь Полный поток падающей волны должен равняться сумме потоков отраженной и прошедшей волн, поскольку полное число нейтронов должно сохраняться. Проверим это обстоятельство. Обозначим через D ширину области на границе, на которую падает нейтронный пучок. Сечения падающего и отраженного пучков будут определяться величиной угла падения D cos θ = D(ken)/ke, а сечение прошедшего углом преломления: D cos θ 0 = D(k 0 n)/k 0. Полный поток нейтронов в падающем пучке: в прошедшем

То есть, полный поток нейтронов, проходящих через некоторую площадку на границе кристалла, определяется только нормальной компонентой волнового вектора. Таким образом, поскольку =1 Тангенциальное движение нейтронов можно совсем исключить из рассмотрения путем перехода в систему отсчета, движущуюся параллельно границе с тангенциальной скоростью нейтрона, поскольку эта составляющая скорости постоянна. При k 0 n обращается в 0, то есть нейтрон перестает распространяться вглубь среды, двигаясь вдоль ее границы (r = 1). Это условие определяет критический угол падения нейтрона, при котором начинается полное отражение нейтрона, которое аналогично полному внутреннему отражению света при переходе из более плотной в менее плотную оптически среду. Для нейтрона "оптическая" плотность среды (по отношению к вакууму) определяется знаком амплитуды рассеяния. Вещество, для которого длины рассеяния положительны (амплитуды отрицательны), как мы увидим, представляют оптически менее плотную, по сравнению с вакуумом, среду.

Итак, начиная с некоторого направления падения, нейтроны будут полностью отражаться кристаллом (r =1). Из условия, определяющего критический угол падения θc, следует: c Это условие имеет простой физический смысл. Оно означает, что полное отражение наступает тогда, когда "поперечная" энергия падающего на кристалл нейтрона (соответствующая нормальному к границе движению) становится меньше среднего потенциала вещества ħ 2 ken 2 /2 m = ħ 2 ke 2 cos 2 θ/2 m ≤ V 0. При этом нормальная компонента волнового вектора становится мнимой, и волна начинает затухать вглубь кристалла. Действительно, при e 2 < ec 2 = V 0 имеем то есть волновая функция начинает затухать по 0 мере проникновения (k 0 n) =k 0 eβ = нейтрона вглубь кристалла: _V Глубина затухания (или проникновения)

На поверхность среды, которая представляет собой потенциальный барьер высотой V 0, падает монохроматический пучок нейтронов с поперечной энергией Ee = ħ 2 ken 2 /2 m. Внутри среды "поперечная" энергия нейтрона уменьшается на величину V 0: E 0 ħ 2 k 0 n 2 /2 m = ħ 2 ken 2 /2 m −V 0. Таким образом, k 0 n 2 (k 0 n)2 =ken 2(1 – 2 m. V 0/ħ 2 ken 2 ) При выходе же из среды даже "покоящийся" в поперечном направлении нейтрон (ось z) приобретет в вакууме энергию E e min =V 0

Эти результаты можно переписать в привычных оптических обозначениях, введя коэффициент преломления n угол падения = π/2 − θ. = k 0/ke и скользящий Критический угол полного отражения, соответственно, будет определяться величиной коэффициента преломления вещества для нейтронов: Учитывая, что ke = 2π / λ, можно написать: =

В результате получаем, что критический угол определяется средним потенциалом кристалла, отнесенным к кинетической энергии нейтрона: Типичные длины рассеяния порядка размера ядра, т. е. моноатомного кристалла (вещества) будем иметь Для нейтронов с длиной волны a 10− 12 см, тогда для λ ~ 0, 1 Å, т. е. ~ 10− 9 см получим Так что т. е. углы полного отражения для тепловых нейтронов порядка нескольких минут. θc = π/2 полное отражение возможно при любых углах. Это произойдет при n = 0, т. е. при V 0 = 1. Другими словами, при кинетических энергиях нейтрона, При меньших величины потенциала вещества, нейтроны не могут проникнуть вглубь вещества и полностью отражаются от стенки.

Граничная энергия нейтронов определяется Граничная длина волны из соотношения: откуда Поскольку N ≈ 1023 см− 3 , a ≈ 10− 12 см, типичная величина граничной длины волны Заметим, что N то λс2 ≈ π · 10− 11 см 2, и λc ≈ 0, 6 · 10− 5 см = 600 Å. = NAρ/A, где ρ — плотность вещества, A — массовое число, NA — число Авогадро, NA ≈ 6, 02 · 1023. Нейтроны с длиной волны, большей граничной, называются ультрахолодными (УХН), их длина волны имеет тот же порядок, что и длина волны обычного света. Они обладают замечательным свойством, они могут храниться в сосуде. Если для тепловых нейтронов c длиной волны λ ≈ 1 Å скорость v ≈ 4· 105 см/с=4000 м/с, то для УХН c λ ≈ 600 Å получим v ≈ 6, 7 м/с. Этой скорости соответствует энергия УХН Ec 2, 3 · 10− 7 э. В. Их можно накапливать в сосуде (полости), если поместить полость на пути пучка нейтронов, например, из реактора.

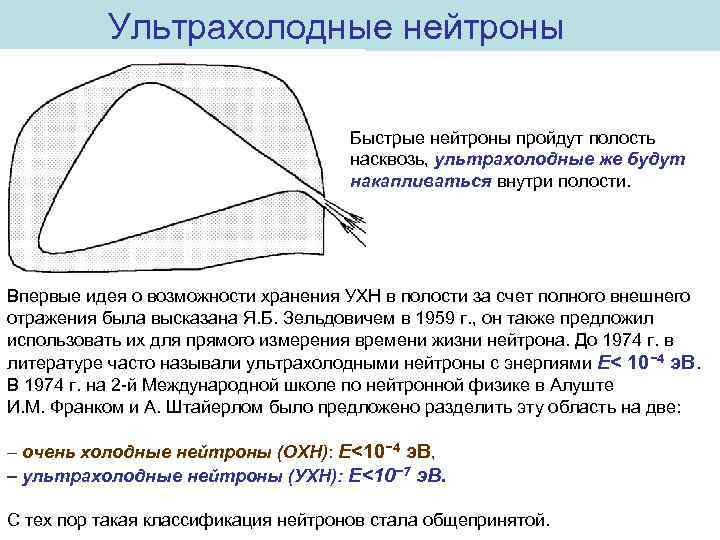Ультрахолодные нейтроны Быстрые нейтроны пройдут полость насквозь, ультрахолодные же будут накапливаться внутри полости. Впервые идея о возможности хранения УХН в полости за счет полного внешнего отражения была высказана Я. Б. Зельдовичем в 1959 г. , он также предложил использовать их для прямого измерения времени жизни нейтрона. До 1974 г. в литературе часто называли ультрахолодными нейтроны с энергиями E< 10− 4 э. В. В 1974 г. на 2 -й Международной школе по нейтронной физике в Алуште И. М. Франком и А. Штайерлом было предложено разделить эту область на две: – очень холодные нейтроны (ОХН): E<10− 4 э. В, – ультрахолодные нейтроны (УХН): E<10− 7 э. В. С тех пор такая классификация нейтронов стала общепринятой.

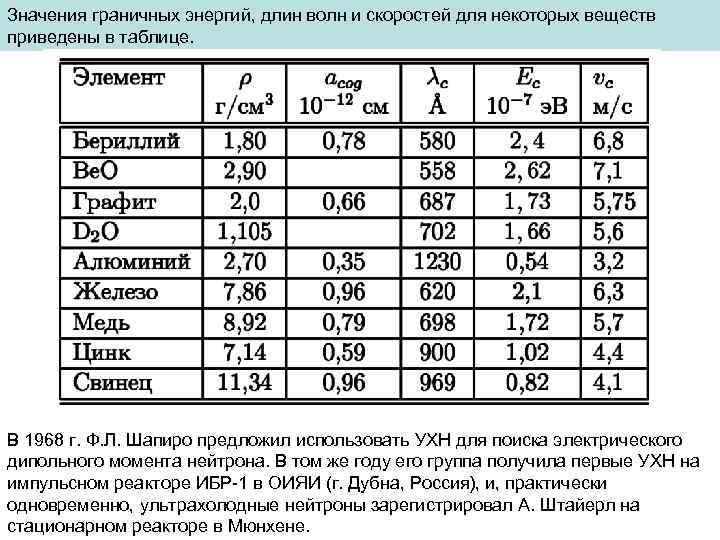Значения граничных энергий, длин волн и скоростей для некоторых веществ приведены в таблице. В 1968 г. Ф. Л. Шапиро предложил использовать УХН для поиска электрического дипольного момента нейтрона. В том же году его группа получила первые УХН на импульсном реакторе ИБР-1 в ОИЯИ (г. Дубна, Россия), и, практически одновременно, ультрахолодные нейтроны зарегистрировал А. Штайерл на стационарном реакторе в Мюнхене.

Однако плотности потоков первых пучков УХН составляли ~10− 3 см− 2 c− 1 (что соответствует плотности нейтронов ~10− 6 н/см 3). УХН было слишком мало для проведения таких экспериментов, как поиск ЭДМ нейтрона или измерение его времени жизни. Причина в следующем. В ядерном реакторе за счет столкновений с атомами замедлителя (это может быть графит или обычная вода) нейтроны находятся в тепловом равновесии с веществом замедлителя, и их спектр приблизительно является максвелловским. Большинство нейтронов имеют энергию вблизи k. T. Отношение же плотности потока нейтронов со скоростями меньшими vc к полной плотности потока (при mvc 2 величину /2 << k. T) составляет При k. T ≈ 0, 025 э. В (T = 300 K) и vc ≈ 6 м/с доля УХН в потоке тепловых нейтронов составит всего ξ ≈ 10− 11. Уменьшая k. T, мы тем самым увеличиваем долю УХН в полном потоке нейтронов. Однако с уменьшением энергии нейтронов (например, при охлаждении замедлителя) увеличивается их длина волны, и, когда она становится больше среднего расстояния между атомами (или молекулами) замедлителя, замедлитель становится „прозрачным“ для нейтронов, они перестают замедляться за счет столкновений с отдельными атомами, термализация прекращается. Дальнейшее замедление нейтронов происходит за счет возбуждения фононов и др. коллективных мод в замедлителе.

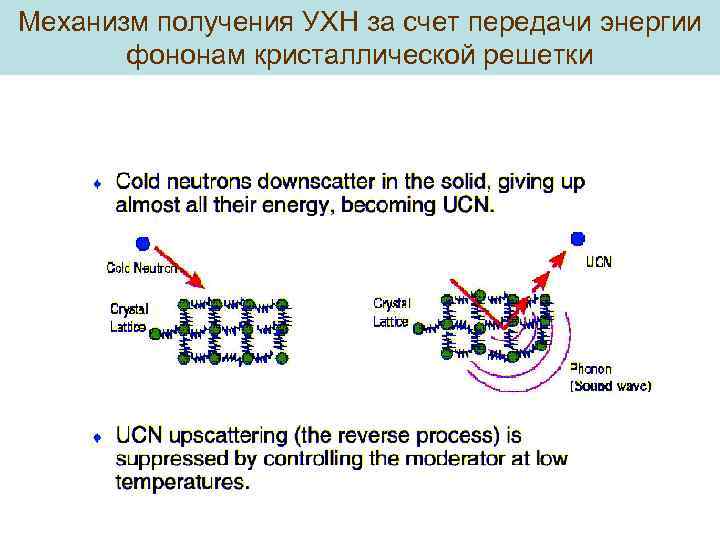Механизм получения УХН за счет передачи энергии фононам кристаллической решетки

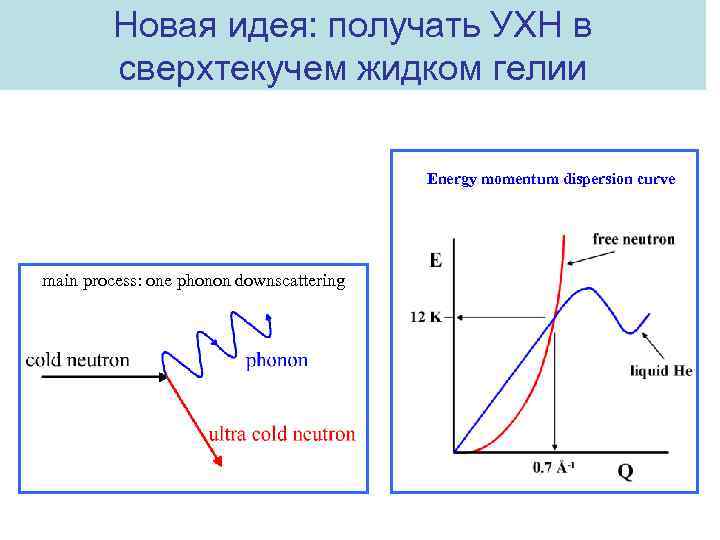Новая идея: получать УХН в сверхтекучем жидком гелии Energy momentum dispersion curve main process: one phonon downscattering

Заметим, что нейтроны, выходящие из вещества, не могут содержать в своем спектре энергий меньших Ec, поскольку будут ускорены на границе. Из графитового замедлителя, например, будут выходить нейтроны со спектром, обрезанным снизу значением 1, 94· 10− 7 э. В (650 Å). При Ec 1 > Ec 0 в полости (расположенной на том же уровне) будут накапливаться нейтроны с Ec 0

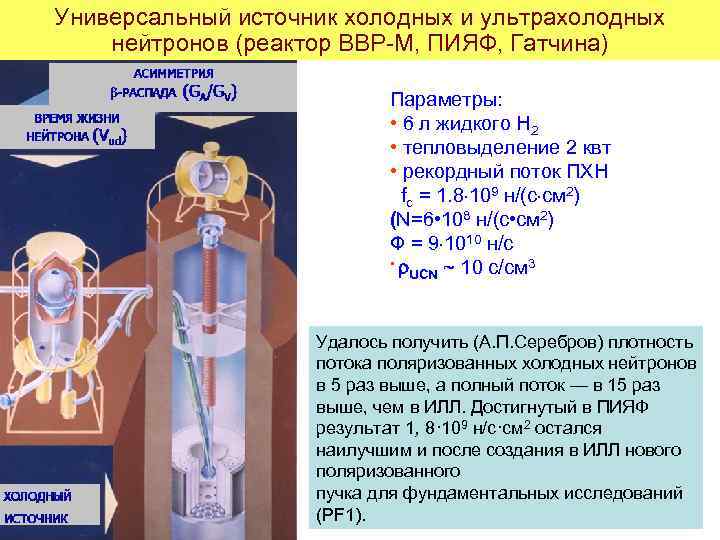Универсальный источник холодных и ультрахолодных нейтронов (реактор ВВР-М, ПИЯФ, Гатчина) Параметры: • 6 л жидкого Н 2 • тепловыделение 2 квт • рекордный поток ПХН fc = 1. 8 109 н/(с см 2) (N=6 • 108 н/(с • см 2) Ф = 9 1010 н/с • 3 UCN ~ 10 с/см Удалось получить (А. П. Серебров) плотность потока поляризованных холодных нейтронов в 5 раз выше, а полный поток — в 15 раз выше, чем в ИЛЛ. Достигнутый в ПИЯФ результат 1, 8· 109 н/с·см 2 остался наилучшим и после создания в ИЛЛ нового поляризованного пучка для фундаментальных исследований (PF 1).

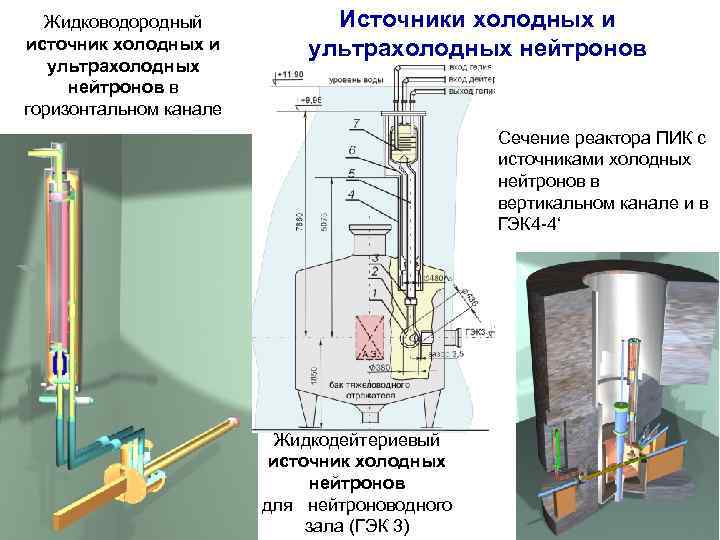Жидководородный источник холодных и ультрахолодных нейтронов в горизонтальном канале Источники холодных и ультрахолодных нейтронов Difractometer for high pressure measurements (JINR, KI) Жидкодейтериевый источник холодных нейтронов для нейтроноводного зала (ГЭК 3) Сечение реактора ПИК с источниками холодных нейтронов в вертикальном канале и в ГЭК 4 -4‘

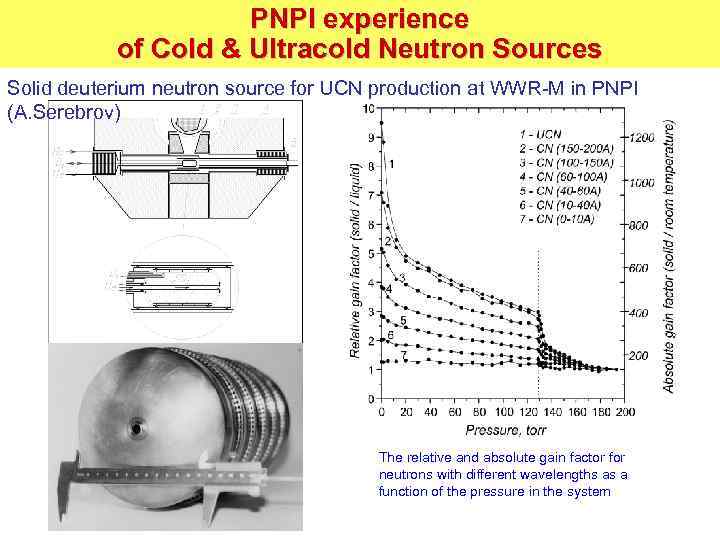PNPI experience of Cold & Ultracold Neutron Sources Solid deuterium neutron source for UCN production at WWR-M in PNPI (A. Serebrov) The relative and absolute gain factor for neutrons with different wavelengths as a function of the pressure in the system

Budapest Cold Neutron Source (A. Serebrov, V. Mityukhlyaev) Cold test of the Cold Neutron Source before installation in the Reactor.

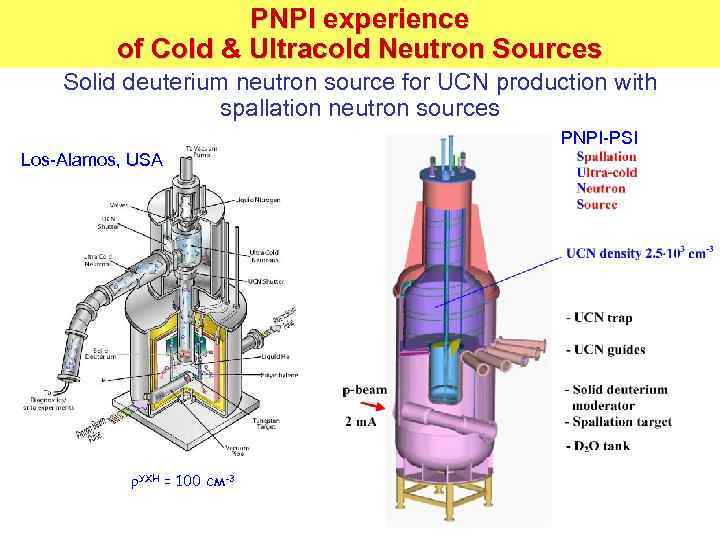PNPI experience Разработка источников УХН в ПИЯФ of Cold & Ultracold Neutron Sources Solid deuterium neutron source for UCN production with spallation neutron sources PNPI-PSI Los-Alamos, USA УХН = 100 см-3

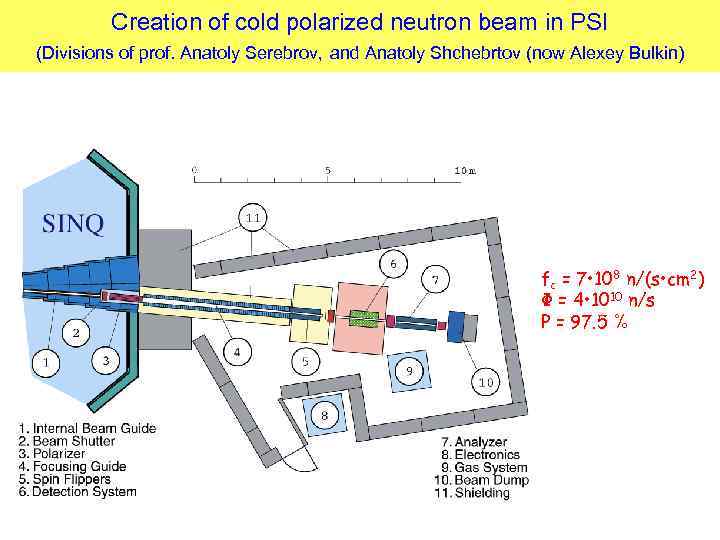Creation of cold polarized neutron beam in PSI (Divisions of prof. Anatoly Serebrov, and Anatoly Shchebrtov (now Alexey Bulkin) fc = 7 • 108 n/(s • cm 2) Ф = 4 • 1010 n/s Р = 97. 5 %

В Институте Пауля–Шерера в Швейцарии для спаллейшн-источника (SINQ) используется ускоритель, где протоны (с током в пучке, достигающем 1, 8 м. А, т. е. ≈ 1016 протонов/с) разгоняются до энергии 590 Мэ. В. Сначала этот пучок проходит через мезонообразующую мишень из углерода, где часть энергии и протонов уходит на производство мезонов, из которых формируются довольно интенсивные пучки пи-мезонов и мюонов для исследований с ними (поэтому такие ускорители называются мезонными фабриками). Оставшийся пучок с током 1, 3 м. А и энергией протонов ≈ 570 Мэ. В (мощность в пучке ≈ 0, 74 МВт) падает на мишень из свинца, где каждый протон выбивает около 10 быстрых нейтронов, которые затем замедляются в тяжеловодном замедлителе. В результате получается источник тепловых нейтронов с плотностью потока ≈ 1014 н/с·см 2, приблизительно такой же, как в реакторе средней мощности. Для дальнейшего замедления нейтронов и получения наибольшего выхода УХН используется твердый дейтерий. Следует отметить, что именно ученые ПИЯФ показали реальную возможность использования твердого дейтерия для существенного увеличения выхода УХН и явились инициаторами и одними из основных разработчиков нового типа источников УХН, создающихся сейчас на мезонных фабриках в Лос-Аламосе (США) и Швейцарии.

Creation of cold polarized neutron beam in PSI

Creation of cold polarized neutron beam in PSI

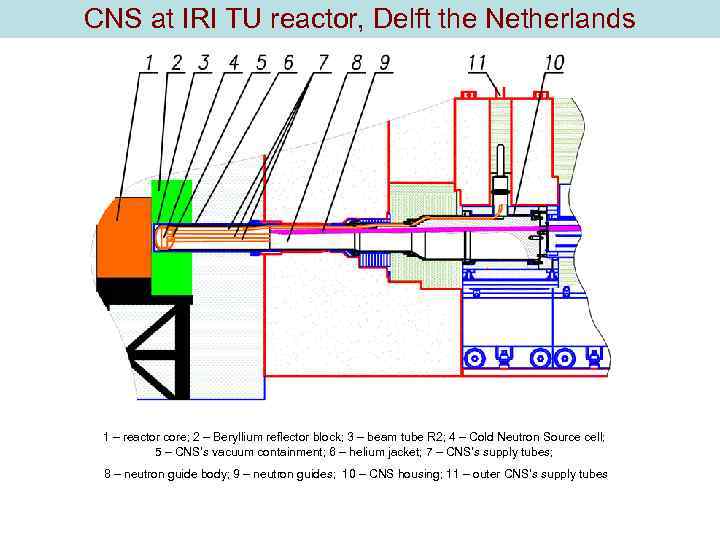CNS at IRI TU reactor, Delft the Netherlands 1 – reactor core; 2 – Beryllium reflector block; 3 – beam tube R 2; 4 – Cold Neutron Source cell; 5 – CNS’s vacuum containment; 6 – helium jacket; 7 – CNS’s supply tubes; 8 – neutron guide body; 9 – neutron guides; 10 – CNS housing; 11 – outer CNS’s supply tubes

CNS for Heavy Water 20 MW reactor ANSTO in Australia (PNPI-INVAP-ANSTO)

Thermosiphon Installation

CNS for Heavy Water 20 MW reactor ANSTO in Australia (PNPI-INVAP-ANSTO) Thermosiphon Installation

CNS Thermosiphon for China

Начнем с проблемы удержания УХН в полости, которая проявилась в первых экспериментах по измерению времени жизни нейтрона, проведенных учеными из Курчатовского института (КИ, Москва) и Научно-исследовательского института атомных реакторов (НИИАР, Димитровград) на димитровградском реакторе СМ-2. Нейтроны удавалось удерживать в ловушке не более сотни секунд. А поскольку время жизни нейтрона около 900 с, это означало, что вероятность потерь за счет взаимодействия со стенками ловушки была почти в 10 раз больше вероятности βраспада. При таких потерях добиться точности измерений лучше одного процента практически невозможно. Был установлен факт потерь УХН за счет нагрева, например, на примесях водорода в поверхности ловушек (нагретый нейтрон покидает ловушку). Однако потери, например, в бериллии все равно оставались больше, чем это следовало из учета такого нагрева и части оптического потенциала, отвечающей за поглощение нейтронов в веществе и, кроме того, имели другую зависимость от энергии нейтрона. Эти добавочные, неизвестной природы, потери УХН возникали с вероятностью ~ 10− 5 на удар при отражении от стенок ловушки и были названы „аномальными потерями“. Природа этих потерь начала проясняться только в самое последнее время.

Чтобы добиться высокой чистоты поверхности и тем самым уменьшить потери, было предложено намораживать кислород на поверхность ловушки с бериллиевым покрытием, которая предварительно прогрета и обезгажена при высоких температурах. В столь большом диапазоне рабочих температур (от 700 до 10 К) трудно сделать надежно работающий и очень плотно закрывающийся затвор для нейтронов. Поэтому была использована идея гравитационного затвора. Сфера с открытым отверстием, которая поворачивается вокруг горизонтальной оси, фактически является гравитационным спектрометром Гравитационное поле и запирает нейтроны в ловушке, причем энергию запертых нейтронов можно менять углом поворота ловушки.

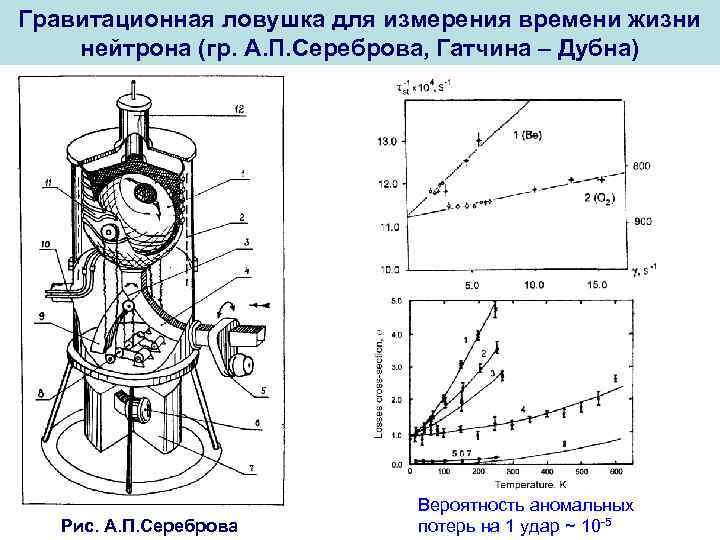Гравитационная ловушка для измерения времени жизни нейтрона (гр. А. П. Сереброва, Гатчина – Дубна) Рис. А. П. Сереброва Вероятность аномальных потерь на 1 удар ~ 10 -5

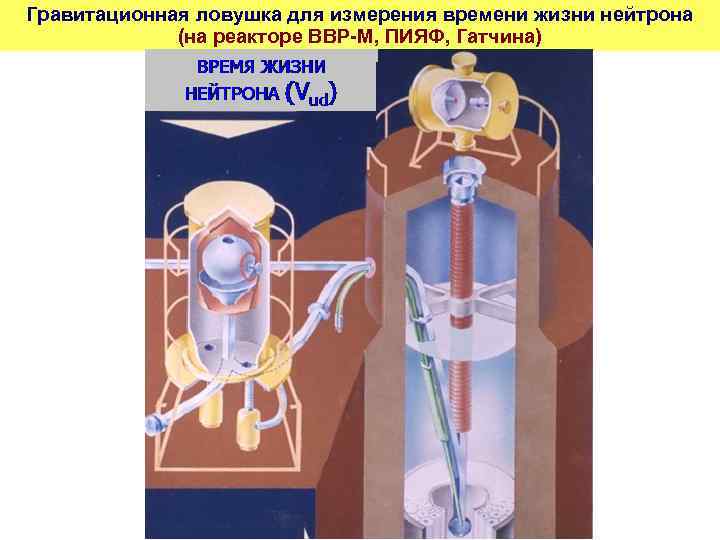Гравитационная ловушка для измерения времени жизни нейтрона (на реакторе ВВР-М, ПИЯФ, Гатчина)

Та же установка для измерения времени жизни нейтрона на реакторе ИЛЛ (Гренобль, Франция)