Нейронные сети_Лекция 2_17_04_2010.ppt
- Количество слайдов: 22

Нейронные сети. Лекция 2 l базовая искусственная модель; l применение нейронных сетей; l процесс обучения нейронной сети; l алгоритмы обучения нейронной сети; l сбор данных для нейронной сети; l пре/пост процессирование; l линейная сеть; l многослойный персептрон; l радиальная базисная функция; l сеть Кохонена; l *примеры.

Базовая искусственная модель Нейронную сеть можно представить себе в виде черного ящика, у которого имеется n входов и m выходов. Кроме этого, имеется набор (матрица) весовых коэффициентов, общее количество которых равно произведению n на m. Элементы, обозначенные цифрами от 1 до m представляют собой слой нейронов. Первый слой сети, на который подаются входные сигналы X 1…Xn, играет роль распределительного слоя нейронной сети имеет связи со всем нейронами следующего слоя, называемого обрабатывающим слоем. Ключевой вопрос – наличие обратной связи. Простейшая сеть имеет структуру прямой передачи сигнала: Сигналы проходят от входов через скрытые элементы и в конце концов приходят на выходные элементы. Такая структура имеет устойчивое поведение. Если же сеть рекуррентная (т. е. содержит связи, ведущие назад от более дальних к более ближним нейронам), то она может быть неустойчива и иметь очень сложную динамику поведения.
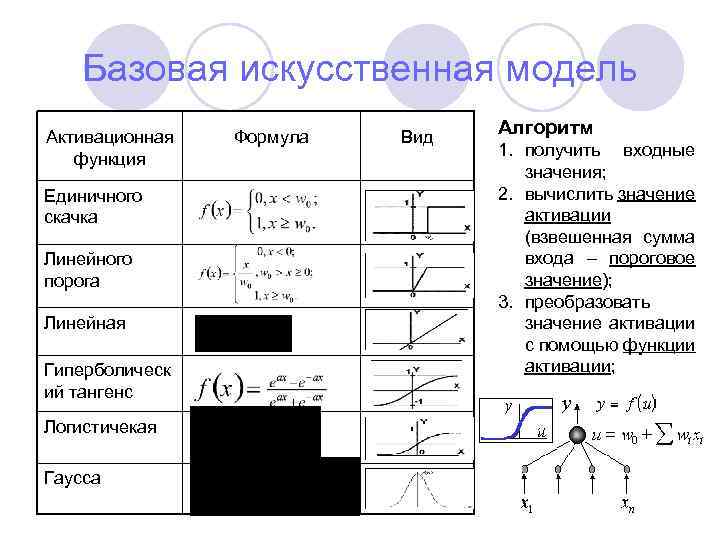
Базовая искусственная модель Активационная функция Единичного скачка Линейного порога Линейная Гиперболическ ий тангенс Логистичекая Гаусса Формула Вид Алгоритм 1. получить входные значения; 2. вычислить значение активации (взвешенная сумма входа – пороговое значение); 3. преобразовать значение активации с помощью функции активации;

Применение нейронных сетей Примеры задач, решаемых с помощью нейронных сетей Прогнозирование на фондовом рынке. Зная цены акций за последнюю рынке. неделю и сегодняшнее значение индекса FTSE, спрогнозировать завтрашнюю цену акций. l Предоставление кредита. Требуется определить, высок ли риск кредита. предоставления кредита частному лицу, обратившемуся с такой просьбой. В результате разговора с ним известен его доход, предыдущая кредитная история и т. д. l Управление. Нужно определить что должен делать робот (повернуться Управление. направо или налево, двигаться вперед и т. д. ), чтобы достичь цели; известно изображение, которое передает установленная на роботе видеокамера. l Особенности применения нейронных сетей для решения задач Сеть можно применять в ситуации, когда у Вас имеется определенная известная информация, и Вы хотите из нее получить некоторую пока неизвестную информацию; l Вы должны знать (или хотя бы иметь серьезные подозрения), что между известными входными значениями и неизвестными выходами имеется связь. l
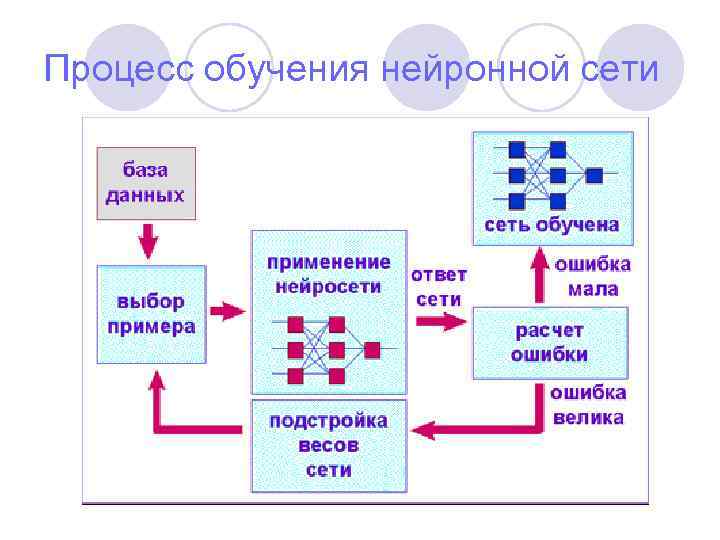
Процесс обучения нейронной сети

Алгоритмы обучения нейронной сети Обучение с учителем 1. 2. Подготавливается набор обучающих данных. Эти данные представляют собой примеры входных данных и соответствующих им выходов. Сеть учится устанавливать связь между первыми и вторыми; Нейронная сеть обучается с помощью того или иного алгоритма управляемого обучения, при котором имеющиеся данные используются для корректировки весов и пороговых значений сети таким образом, чтобы минимизировать ошибку прогноза на обучающем множестве. Обучение без учителя Обучающие данные содержат только значения входных переменных.

Сбор данных для нейронной сети Причины, ухудшающие качество обучающего множества: l l l Нерепрезентативность данных; Будущее не похоже на прошлое; Следует учесть все возможности; Сеть обучается тому, чему проще всего обучиться; Несбалансированный набор данных.

Сбор данных для нейронной сети Основные вопросы: l l l Какие свойства и признаки объекта исследования брать в качестве входных значений? Проводить ли перевод из одной шкалы в другую? Проводить ли нормировку значений? Сколько наблюдений необходимо иметь для обучения сети? Что делать с не вполне достоверными данными (шумы, аномалии, пропуски)?

Сбор данных для нейронной сети Выводы: Выбирайте такие переменные, которые, как Вы предполагаете, влияют на результат; l С числовыми и номинальными переменными можно работать непосредственно*. Переменные других типов следует преобразовать в указанные типы или объявить незначащими; l Чем больше в задаче переменных, тем больше нужно иметь наблюдений; l В случае необходимости можно работать с наблюдениями, содержащими пропущенные значения. Если возможно, удалите выбросы. Если данных достаточное количество, уберите из рассмотрения наблюдения с пропущенными значениями. l
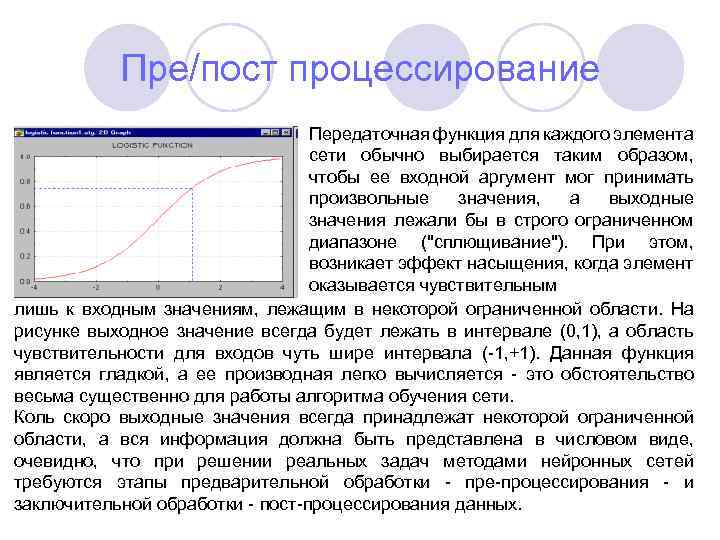
Пре/пост процессирование Передаточная функция для каждого элемента сети обычно выбирается таким образом, чтобы ее входной аргумент мог принимать произвольные значения, а выходные значения лежали бы в строго ограниченном диапазоне ("сплющивание"). При этом, возникает эффект насыщения, когда элемент оказывается чувствительным лишь к входным значениям, лежащим в некоторой ограниченной области. На рисунке выходное значение всегда будет лежать в интервале (0, 1), а область чувствительности для входов чуть шире интервала (-1, +1). Данная функция является гладкой, а ее производная легко вычисляется - это обстоятельство весьма существенно для работы алгоритма обучения сети. Коль скоро выходные значения всегда принадлежат некоторой ограниченной области, а вся информация должна быть представлена в числовом виде, очевидно, что при решении реальных задач методами нейронных сетей требуются этапы предварительной обработки - пре-процессирования - и заключительной обработки - пост-процессирования данных.

Пре/пост процессирование Шкалирование Числовые значения должны быть приведены в масштаб, подходящий для сети. Обычно исходные данные масштабируются по линейной шкале*. Номинальные переменные Номинальная переменная числовая переменная (Пол = {Муж, Жен} Муж = 0, Жен = 1) l Кодирование 1 -из-N: (Животное = {Собака, Овца, Кошка} Собака = {1, 0, 0}, Овца = {0, 1, 0}, Кошка = {0, 0, 1}) l
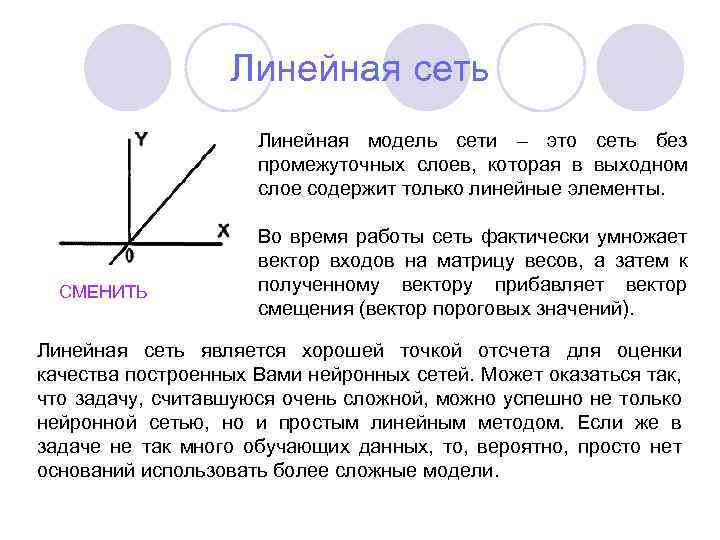
Линейная сеть Линейная модель сети – это сеть без промежуточных слоев, которая в выходном слое содержит только линейные элементы. СМЕНИТЬ Во время работы сеть фактически умножает вектор входов на матрицу весов, а затем к полученному вектору прибавляет вектор смещения (вектор пороговых значений). Линейная сеть является хорошей точкой отсчета для оценки качества построенных Вами нейронных сетей. Может оказаться так, что задачу, считавшуюся очень сложной, можно успешно не только нейронной сетью, но и простым линейным методом. Если же в задаче не так много обучающих данных, то, вероятно, просто нет оснований использовать более сложные модели.
Многослойных персептрон Обучение многослойного персептрона Целью обучения является поиск таких значений весов и порогов сети, которые бы минимизировали ошибку прогноза, выдаваемого сетью. Функции ошибок: l сумма квадратов ошибок; l среднеквадратическая ошибка. Поверхности ошибок: l параболоид; l сложная форма (с множеством глобальных минимумов).
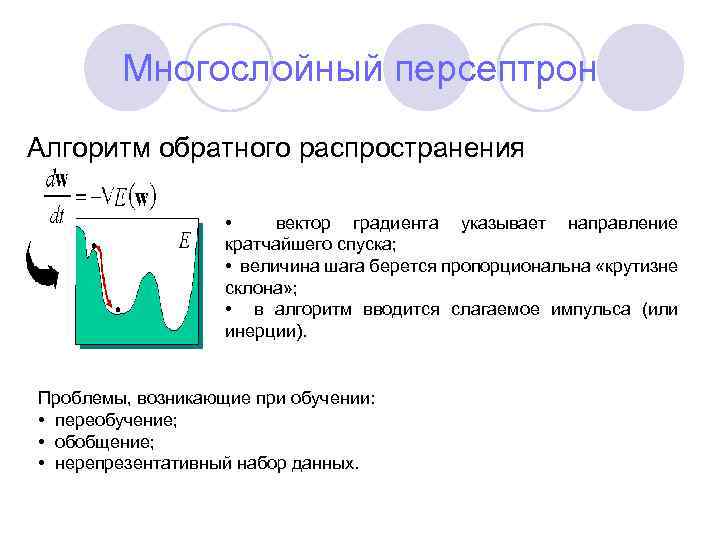
Многослойный персептрон Алгоритм обратного распространения • вектор градиента указывает направление кратчайшего спуска; • величина шага берется пропорциональна «крутизне склона» ; • в алгоритм вводится слагаемое импульса (или инерции). Проблемы, возникающие при обучении: • переобучение; • обобщение; • нерепрезентативный набор данных.

Радиальная базисная функция Отличия сетей RBF от сетей MLP: Используется для разбиения пространства входных данных окружностями или (в общем случае) гиперсферами. • моделируют произвольную нелинейную функцию с помощью всего одного промежуточного слоя; • сети с RBF обучается на порядок быстрее MLP; • «групповое» представление пространства модели (в отличие от «плоскостного» ); • при удалении от обучающего множества значение функции отклика быстро спадает до нуля; • сети с RBF более чувствительны к «проклятию размерности» • сети с RBF испытывают трудности, когда число входов велико.

Радиальная базисная функция Обучение RBF-сети проходит в несколько этапов: 1. Определяются центры и отклонения для радиальных элементов; 2. Оптимизируются параметры линейного выходного слоя. Расположение центров должно соответствовать кластерам, реально присутствующим в исходных данных. Рассмотрим два наиболее часто используемых метода: • выборка из выборки; • алгоритм К-средних. После того, как определено расположение центров, нужно найти отклонения. Величина отклонения определяет «остроту» гауссовой функции. Используют несколько методов: • явный; • изотропный; • К ближайших соседей.
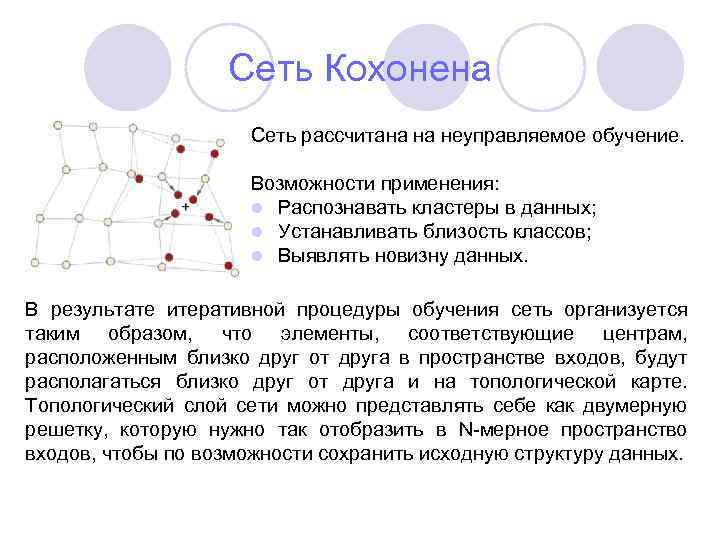
Сеть Кохонена Сеть рассчитана на неуправляемое обучение. Возможности применения: l Распознавать кластеры в данных; l Устанавливать близость классов; l Выявлять новизну данных. В результате итеративной процедуры обучения сеть организуется таким образом, что элементы, соответствующие центрам, расположенным близко друг от друга в пространстве входов, будут располагаться близко друг от друга и на топологической карте. Топологический слой сети можно представлять себе как двумерную решетку, которую нужно так отобразить в N-мерное пространство входов, чтобы по возможности сохранить исходную структуру данных.

Сеть Кохонена На каждой эпохе алгоритм обрабатывает каждый из обучающих примеров, и затем применяет следующий алгоритм: • выбрать выигравший нейрон (то есть тот, который расположен ближе всего к входному примеру); • скорректировать выигравший нейрон так, чтобы он стал более похож на этот входной пример (взяв взвешенную сумму прежнего центра нейрона и обучающего примера). После того, как сеть обучена распознаванию структуры данных, ее можно использовать как средство визуализации при анализе данных, при котором можно определить разбивается ли карта на отдельные кластеры. Далее, как только кластеры выявлены, нейроны топологической карты помечаются содержательными по смыслу метками (в некоторых случаях помечены могут быть и отдельные наблюдения).
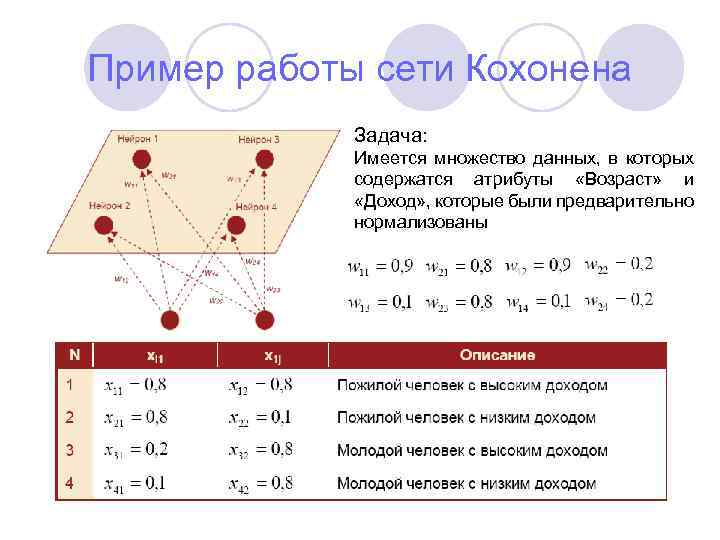
Пример работы сети Кохонена Задача: Имеется множество данных, в которых содержатся атрибуты «Возраст» и «Доход» , которые были предварительно нормализованы
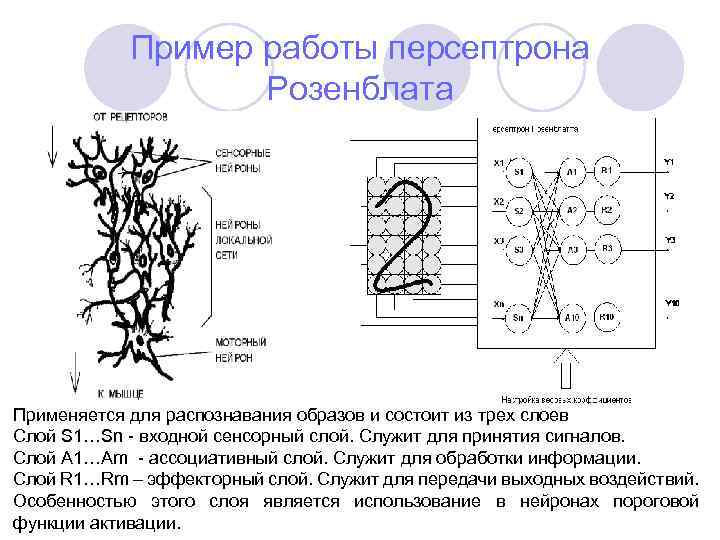
Пример работы персептрона Розенблата Применяется для распознавания образов и состоит из трех слоев Слой S 1…Sn - входной сенсорный слой. Служит для принятия сигналов. Слой A 1…Am - ассоциативный слой. Служит для обработки информации. Слой R 1…Rm – эффекторный слой. Служит для передачи выходных воздействий. Особенностью этого слоя является использование в нейронах пороговой функции активации.

Пример реализации нейронных сетей в Matlab
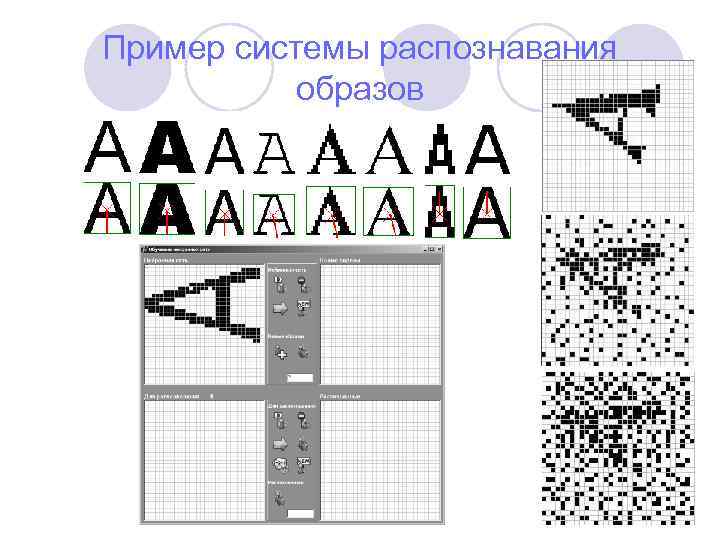
Пример системы распознавания образов
Нейронные сети_Лекция 2_17_04_2010.ppt