Неинерциальные системы отсчета 1 К система

Неинерциальные системы отсчета 1

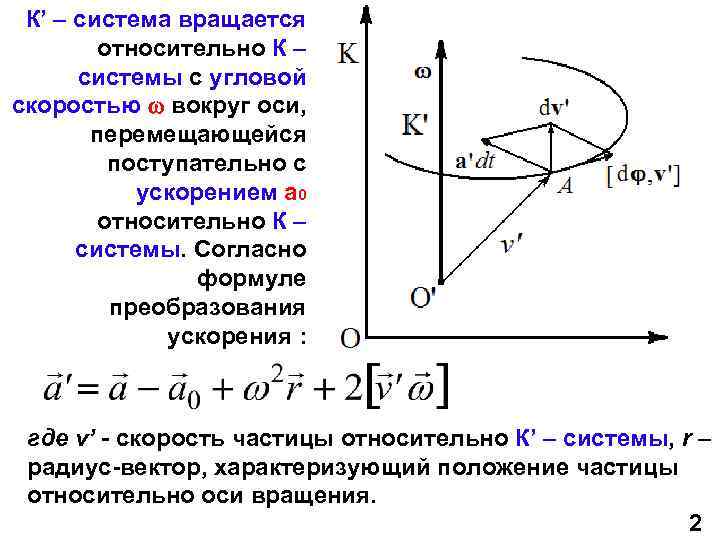К’ – система вращается относительно К – системы с угловой скоростью вокруг оси, перемещающейся поступательно с ускорением а 0 относительно К – системы. Согласно формуле преобразования ускорения : где v’ - скорость частицы относительно К’ – системы, r – радиус-вектор, характеризующий положение частицы относительно оси вращения. 2

Умножая обе части равенства на m и учитывая, что в инерциальной системе отсчета имеем: Это и есть основное уравнение динамики в неинерциальной системе отсчета. Частица в неинерциальной системе отсчета будет двигаться с ускорением при 3

Силы инерции Перепишем уравнение динамки для неинерциальной системы отсчета в виде: где - поступательная сила инерции - центробежная сила инерции - сила Кориолиса (кориолисова сила инерции) Силы инерции зависят от свойств неинерциальной системы отсчета 4

Особенности сил инерции 1. Силы инерции обусловлены свойствами неинерциальных систем отсчета. 2. Эти силы существуют только в неинерциальных системах отсчета. 3. Все силы инерции, подобно силам тяготения, пропорциональны массе тела. Поэтому в однородном поле сил инерции, как и в поле сил тяготения, все тела движутся с одним и тем же ускорением независимо от их масс. 5

Принцип эквивалентности Никакими физическими опытами невозможно отличить однородное поле сил тяготения от однородного поля сил инерции. Этот постулат составляет содержание принципа эквивалентности сил тяготения и сил инерции: все физические явления в однородном поле сил тяготения происходят совершенно так же, как и в соответствующем однородном поле инерции. 6

РЕЛЯТИВИСТСКАЯ МЕХАНИКА Кинематика специальной теории относительности (СТО) 7

До опубликования в 1905 г. Эйнштейном теории относительности существовала идея «светового эфира» . С этой средой связывали «абсолютную» систему координат. Для проверки это предположения были поставлены опыты Майкельсона и Морли Цель эксперимента – обнаружить истинное движение Земли относительно «эфира» используя ее орбитальное движение (30 км/с). 8

Опыты Майкельсона Свет распространялся в перпендикулярных направлениях и сравнивалось время прохождения светом путей SAS и SBS. Если справедлив обычный закон сложения скоростей, то на пути SA скорость света относительно Земли равна c - V , а на обратном пути c + V. Тогда время прохождения пути SAS : На пути SBS скорость света относительно Земли равна и Разность времен не была обнаружена. Свет от источника всегда распространяется со скоростью c независимо от направления движения источника (приемника) света. 9

Исходные постулаты СТО Принцип относительности Галилей Законы механики инвариантны относительно ИСО Эйнштейн Все законы физики инвариантны относительно ИСО Основной постулат СТО Существует такая скорость передачи взаимодействий, которая одинакова во всех ИСО – скорость света Дополнительный постулат СТО Согласно принципу относительности Галилея время и пространство абсолютны В СТО оба эти положения отвергаются И вводится дополнительный (к основному) постулат. Величину ds называют интервалом 10

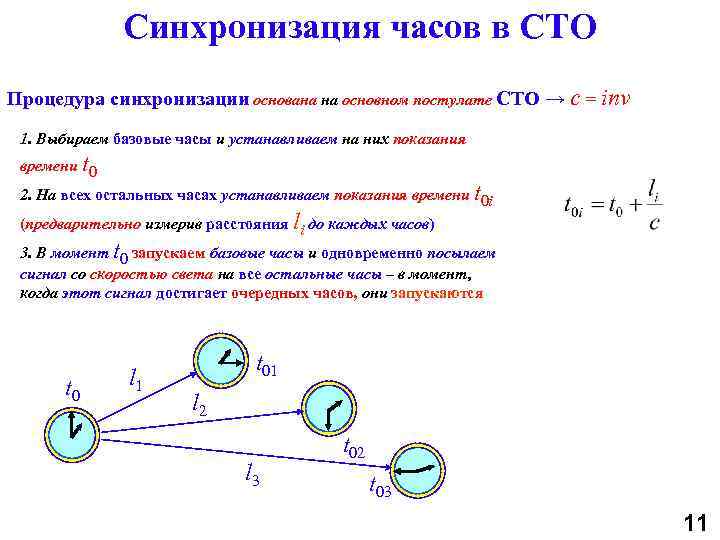Синхронизация часов в СТО Процедура синхронизации основана на основном постулате СТО → c = inv 1. Выбираем базовые часы и устанавливаем на них показания времени t 0 2. На всех остальных часах устанавливаем показания времени t 0 i (предварительно измерив расстояния li до каждых часов) 3. В момент t 0 запускаем базовые часы и одновременно посылаем сигнал со скоростью света на все остальные часы – в момент, когда этот сигнал достигает очередных часов, они запускаются t 0 l 1 t 01 l 2 l 3 t 02 t 03 11

Преобразования Лоренца 12

Промежутки времени в различных ИСО Рассмотрим две ИСО, движущиеся вдоль осей X-ов Y' Y K' K 0 dl Время в системе покоя называют собственным и обозначают τ (у нас τ=t') Z Время во всех остальных ИСО называют мировым и обозначают t R 1 Очевидно Z' v X' X где введено обозначение: γ - релятивистский фактор (Лоренц-фактор) промежутки времени по собственным часам всегда минимальны 13

Длина отрезка в различных ИСО Рассмотрим две ИСО, движущиеся вдоль осей X-ов Y Y' K' K l 0 - длина стержня в той системе, где он находится в покое (в – ИСО K') Время в системе, где часы находятся в покое является собственным Z v l 0 Z' X' X Тогда очевидно R 2 где γ - релятивистский фактор (Лоренц-фактор) Таким образом Длина стержня в системе покоя (собственная длина) всегда максимальна 14

Преобразования Лоренца Рассмотрим событие A из ИСО K и K' Сначала будем проводить измерения из ИСО K' R 3 При измерениях из ИСО K R 3 Y' Y K' K vt O Имеем A x' O' z' Z z Z' Тогда очевидно v x X X' R 4 15

Преобразования Лоренца при переходе от K - к K’ – системе имеют вид: При обратном переходе от K’ - к K – системе Преобразования Лоренца при V << c переходят в преобразования Галилея. 16

Закон сложения скоростей в СТО Рассмотрим произвольно движущуюся материальную точку из двух ИСО K и K' По определению Следовательно нам нужно найти связь И мы получаем Y' Y K' K R 5 Закон сложения скоростей для компоненты скорости точки вдоль скорости ИСО K' Далее Откуда несложно получить R 6 O Z O' v v X X' Z' Закон сложения скоростей для нормальных компонент скорости 17

Экспериментальное подтверждение СТО Эффекты сокращения масштабов и замедления времени: математические «издержки» ? . . или… физическая реальность? Время жизни - мезона в системе отсчета, связанной с частицей = 2, 6 10 -8 с. Скорость мезонов v=0, 75 c, следовательно пройденный путь должен быть 18

Экспериментальное подтверждение СТО Экспериментально измеренное расстояние Если учесть, что - мезоны являются движущимися часами, для правильного описания явления, время жизни - мезона нужно преобразовать к системе отсчета наблюдателя: Тогда, среднее расстояние: Это значение согласуется с экспериментом. 19