 НАХОЖДЕНИЕ ПРОИЗВОДНЫХ И ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ В EXCEL Подготовила Дьяченко Анастасия
НАХОЖДЕНИЕ ПРОИЗВОДНЫХ И ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ В EXCEL Подготовила Дьяченко Анастасия
 ПРОИЗВОДНАЯ Производной функции y=f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
ПРОИЗВОДНАЯ Производной функции y=f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
 Существуют различные формулы численного дифференцирования. Из них простейшими являются явные трехточечные формулы, в частности:
Существуют различные формулы численного дифференцирования. Из них простейшими являются явные трехточечные формулы, в частности:
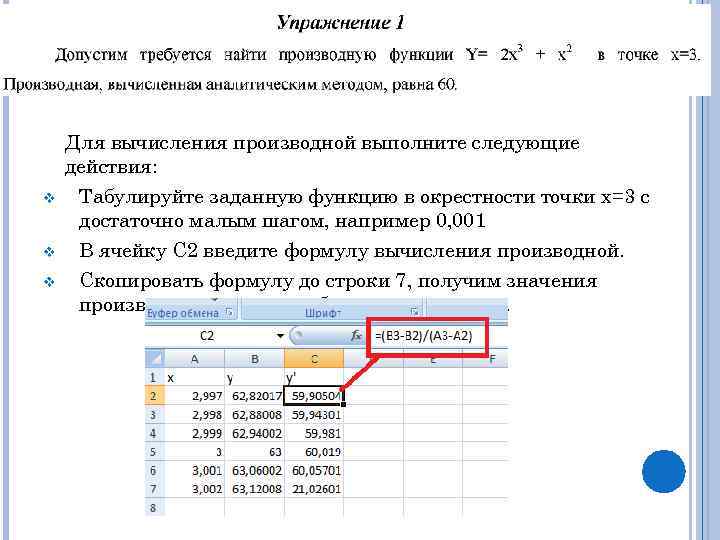 Для вычисления производной выполните следующие действия: v v v Табулируйте заданную функцию в окрестности точки х=3 с достаточно малым шагом, например 0, 001 В ячейку С 2 введите формулу вычисления производной. Скопировать формулу до строки 7, получим значения производных в точках табуляции аргумента.
Для вычисления производной выполните следующие действия: v v v Табулируйте заданную функцию в окрестности точки х=3 с достаточно малым шагом, например 0, 001 В ячейку С 2 введите формулу вычисления производной. Скопировать формулу до строки 7, получим значения производных в точках табуляции аргумента.
![УПРАЖНЕНИЕ 2 Найти производную функции y=sinx на промежутке [0; 6, 2] при шаге дискретизации УПРАЖНЕНИЕ 2 Найти производную функции y=sinx на промежутке [0; 6, 2] при шаге дискретизации](https://present5.com/presentation/19259678_107946883/image-5.jpg) УПРАЖНЕНИЕ 2 Найти производную функции y=sinx на промежутке [0; 6, 2] при шаге дискретизации ∆х=0, 2. v Ввести значения аргумента и значения ф-ции
УПРАЖНЕНИЕ 2 Найти производную функции y=sinx на промежутке [0; 6, 2] при шаге дискретизации ∆х=0, 2. v Ввести значения аргумента и значения ф-ции
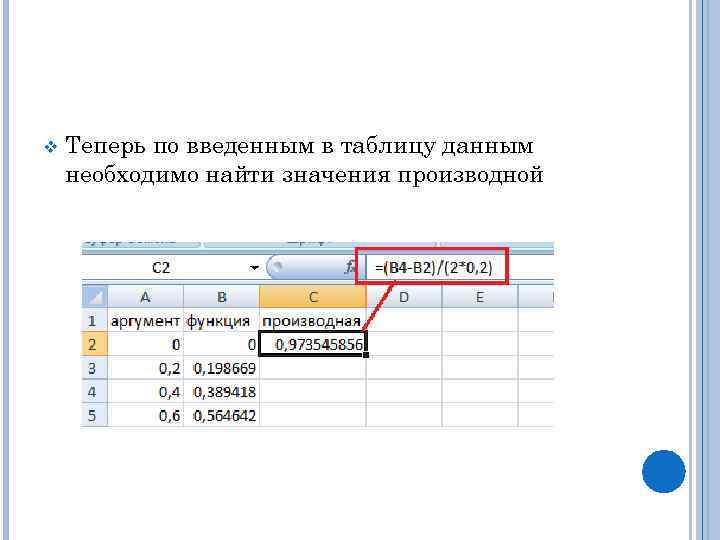 v Теперь по введенным в таблицу данным необходимо найти значения производной
v Теперь по введенным в таблицу данным необходимо найти значения производной
 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x=a и x=b и графиком функции f(x)
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x=a и x=b и графиком функции f(x)
 Существует значительное количество методов вычисления интегралов. Мы рассмотрим лишь несколько: 1) Как сумма элементарных прямоугольниковметод прямоугольников
Существует значительное количество методов вычисления интегралов. Мы рассмотрим лишь несколько: 1) Как сумма элементарных прямоугольниковметод прямоугольников
 1) Как суммы элементарных трапеций – метод трапеций
1) Как суммы элементарных трапеций – метод трапеций
 УПРАЖНЕНИЕ 1 Методом прямоугольников и методом трапеций найти с шагом ∆х=0, 1.
УПРАЖНЕНИЕ 1 Методом прямоугольников и методом трапеций найти с шагом ∆х=0, 1.
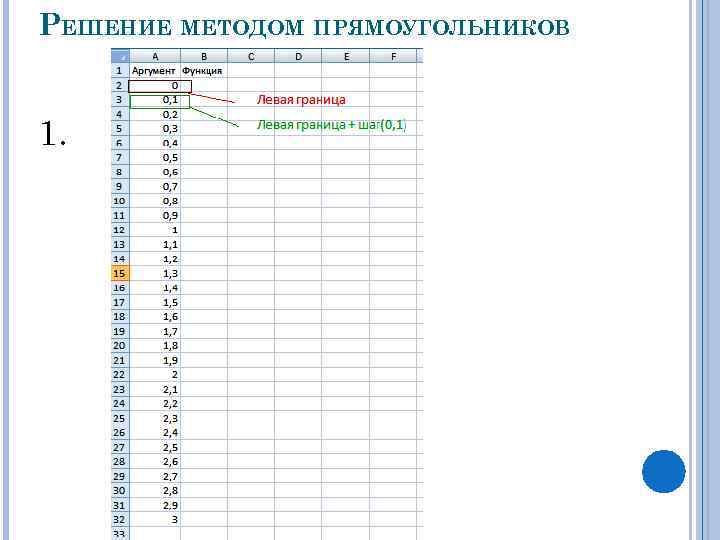 РЕШЕНИЕ МЕТОДОМ ПРЯМОУГОЛЬНИКОВ 1.
РЕШЕНИЕ МЕТОДОМ ПРЯМОУГОЛЬНИКОВ 1.
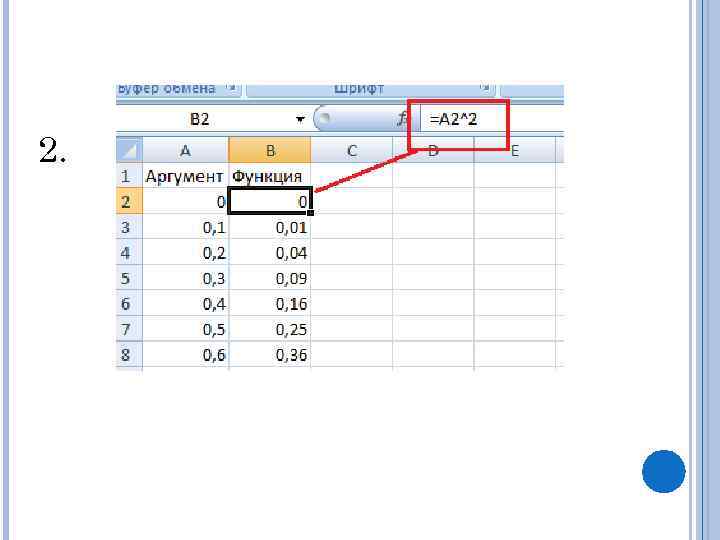 2.
2.
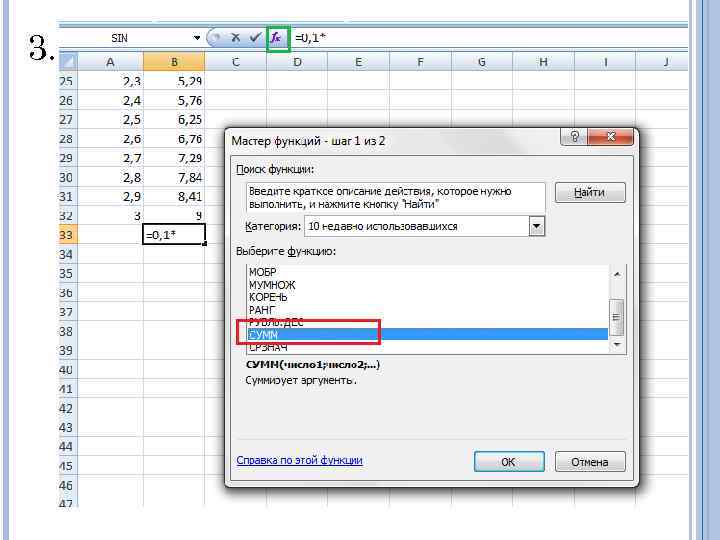 3.
3.
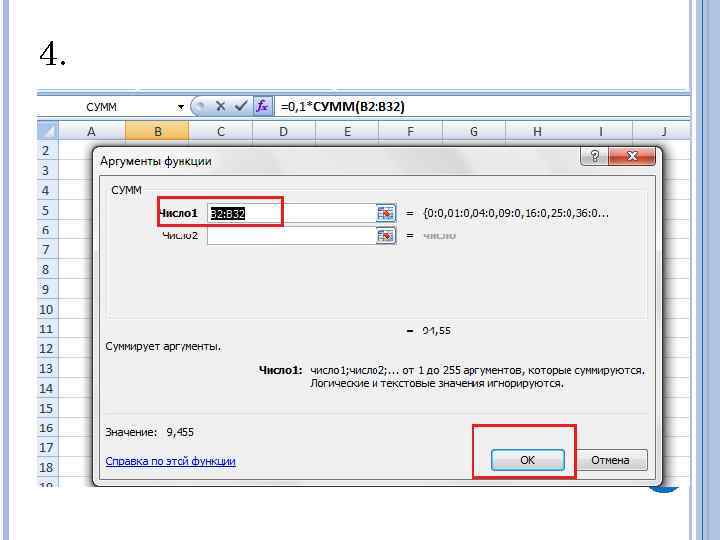 4.
4.
 И получаем значение интеграла
И получаем значение интеграла
 Вычислим значение интеграла аналитически Таким образом ошибка приближения метода прямоугольников в данном случае довольна значительна – 0, 455
Вычислим значение интеграла аналитически Таким образом ошибка приближения метода прямоугольников в данном случае довольна значительна – 0, 455
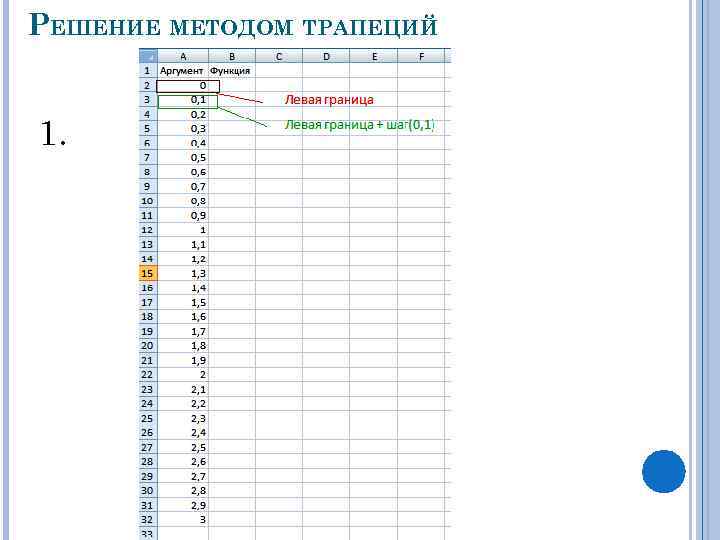 РЕШЕНИЕ МЕТОДОМ ТРАПЕЦИЙ 1.
РЕШЕНИЕ МЕТОДОМ ТРАПЕЦИЙ 1.
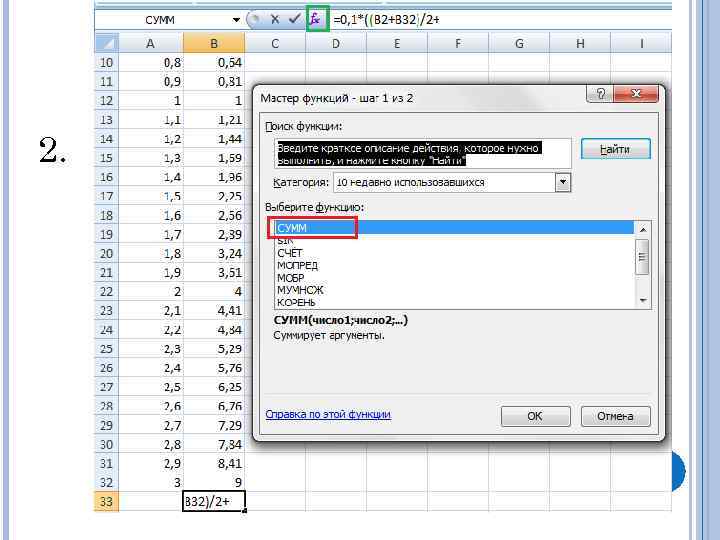 2.
2.
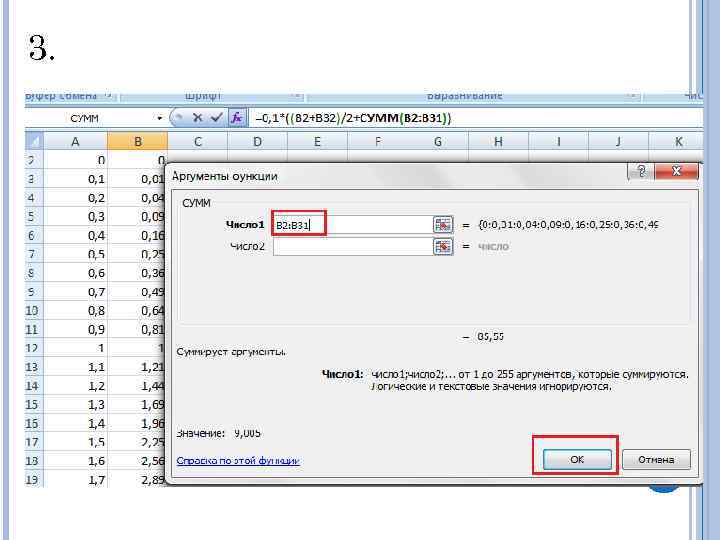 3.
3.
 Получаем значение интеграла
Получаем значение интеграла
 Ошибка приближения метода трапеций в данном случае вполне приемлемая – 0, 005
Ошибка приближения метода трапеций в данном случае вполне приемлемая – 0, 005