Нахождение площади сечения С 2 Учитель математики МБОУ СОШ № 25 г. Крымска Е. В. Малая
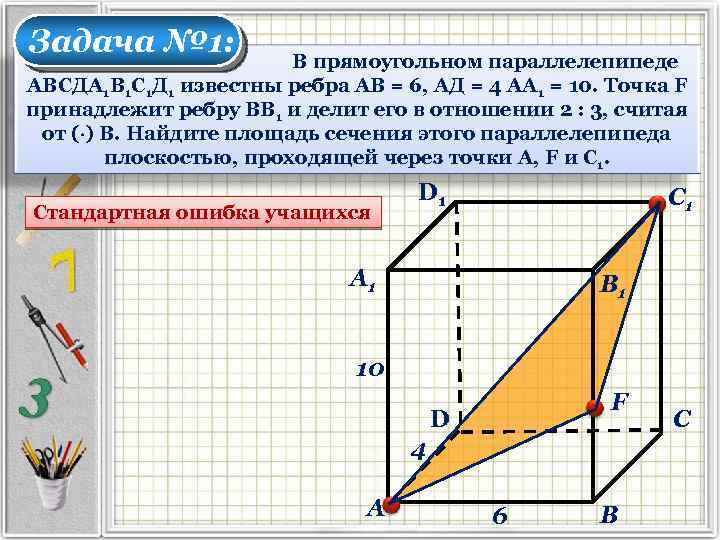
Задача № 1: В прямоугольном параллелепипеде АВСДА 1 В 1 С 1 Д 1 известны ребра АВ = 6, АД = 4 АА 1 = 10. Точка F принадлежит ребру ВВ 1 и делит его в отношении 2 : 3, считая от ( ) В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С 1. Стандартная ошибка учащихся D 1 С 1 А 1 В 1 10 F D 4 А 6 В С
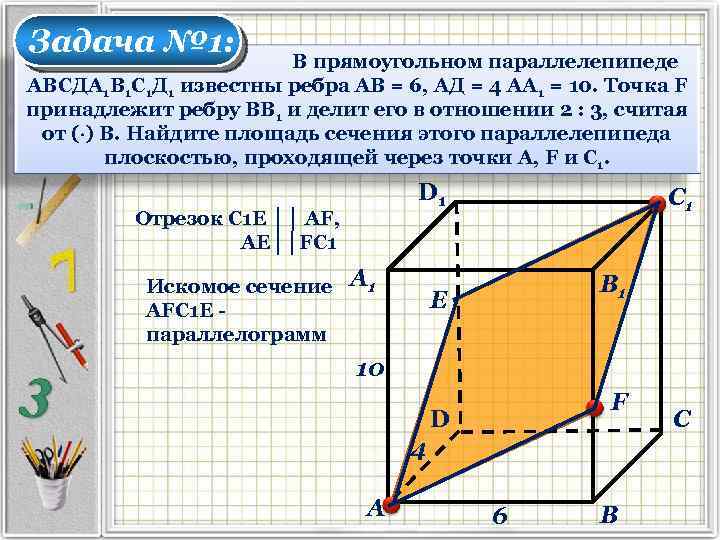
Задача № 1: В прямоугольном параллелепипеде АВСДА 1 В 1 С 1 Д 1 известны ребра АВ = 6, АД = 4 АА 1 = 10. Точка F принадлежит ребру ВВ 1 и делит его в отношении 2 : 3, считая от ( ) В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С 1. D 1 Отрезок С 1 Е ││ АF, АЕ││FС 1 Искомое сечение АFС 1 Е параллелограмм А 1 С 1 В 1 Е 10 F D 4 А 6 В С
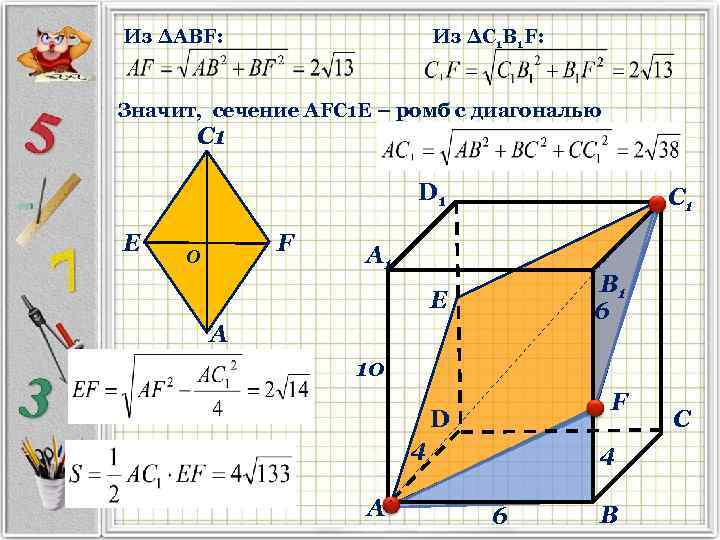
Из ΔАВF: Из ΔС 1 В 1 F: Значит, сечение АFС 1 Е – ромб с диагональю С 1 D 1 Е F О С 1 А 1 В 1 6 Е А 10 F D 4 А 4 6 В С
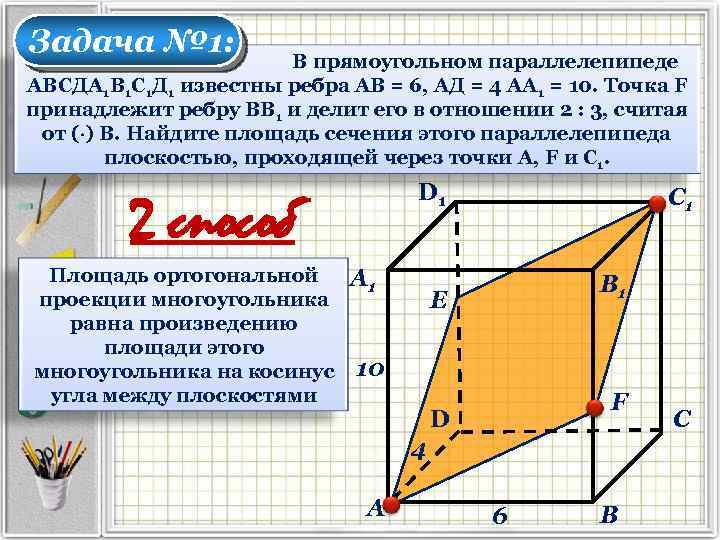
Задача № 1: В прямоугольном параллелепипеде АВСДА 1 В 1 С 1 Д 1 известны ребра АВ = 6, АД = 4 АА 1 = 10. Точка F принадлежит ребру ВВ 1 и делит его в отношении 2 : 3, считая от ( ) В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С 1. D 1 2 способ Площадь ортогональной проекции многоугольника равна произведению площади этого многоугольника на косинус угла между плоскостями А 1 С 1 В 1 Е 10 F D 4 А 6 В С
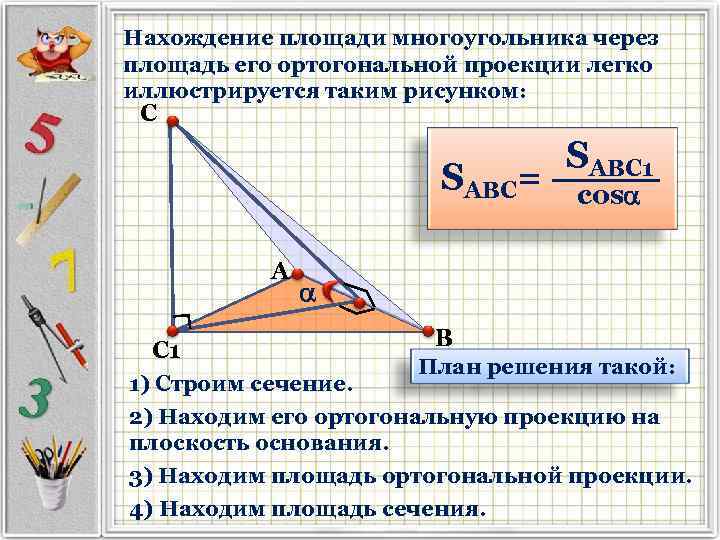
Нахождение площади многоугольника через площадь его ортогональной проекции легко иллюстрируется таким рисунком: С SАВС= А С 1 SАВС 1 соs В План решения такой: 1) Строим сечение. 2) Находим его ортогональную проекцию на плоскость основания. 3) Находим площадь ортогональной проекции. 4) Находим площадь сечения.
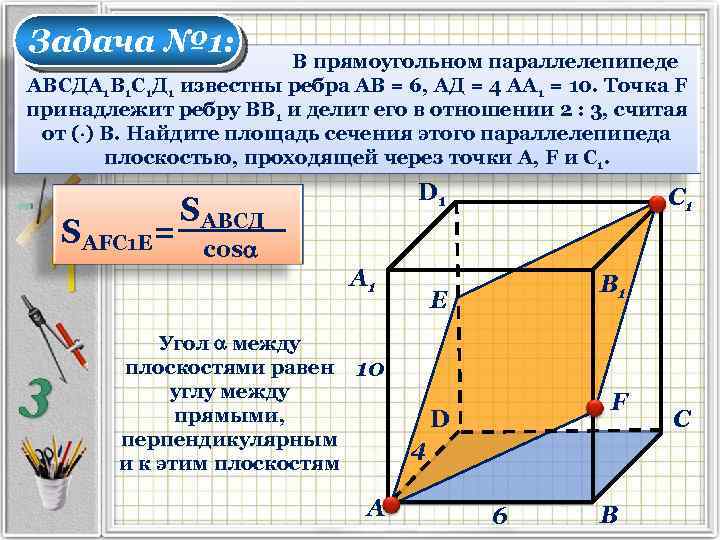
Задача № 1: В прямоугольном параллелепипеде АВСДА 1 В 1 С 1 Д 1 известны ребра АВ = 6, АД = 4 АА 1 = 10. Точка F принадлежит ребру ВВ 1 и делит его в отношении 2 : 3, считая от ( ) В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С 1. SАFС 1 Е= D 1 SАВСД С 1 соs А 1 Угол между плоскостями равен углу между прямыми, перпендикулярным и к этим плоскостям В 1 Е 10 F D 4 А 6 В С
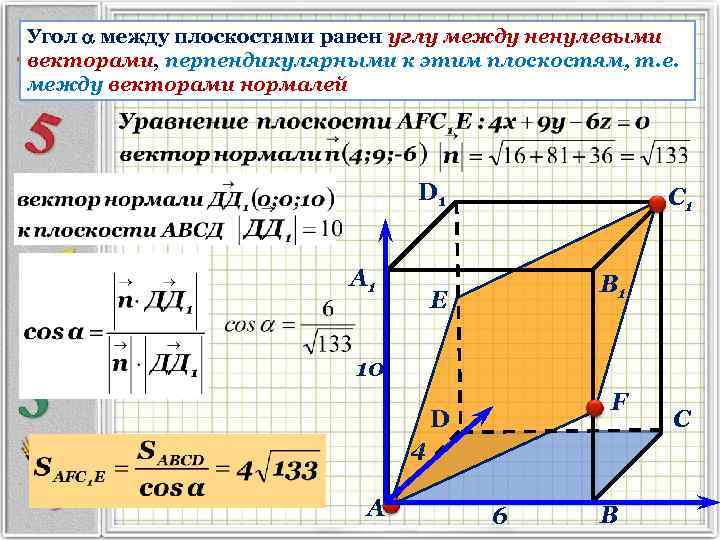
Угол между плоскостями равен углу между ненулевыми векторами, перпендикулярными к этим плоскостям, т. е. между векторами нормалей D 1 А 1 С 1 В 1 Е 10 F D 4 А 6 В С
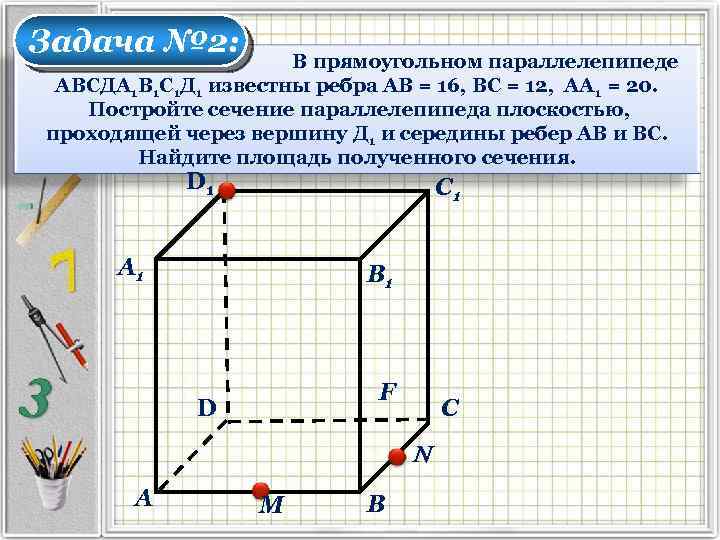
Задача № 2: В прямоугольном параллелепипеде АВСДА 1 В 1 С 1 Д 1 известны ребра АВ = 16, ВС = 12, АА 1 = 20. Постройте сечение параллелепипеда плоскостью, проходящей через вершину Д 1 и середины ребер АВ и ВС. Найдите площадь полученного сечения. D 1 С 1 А 1 В 1 F D С А М В
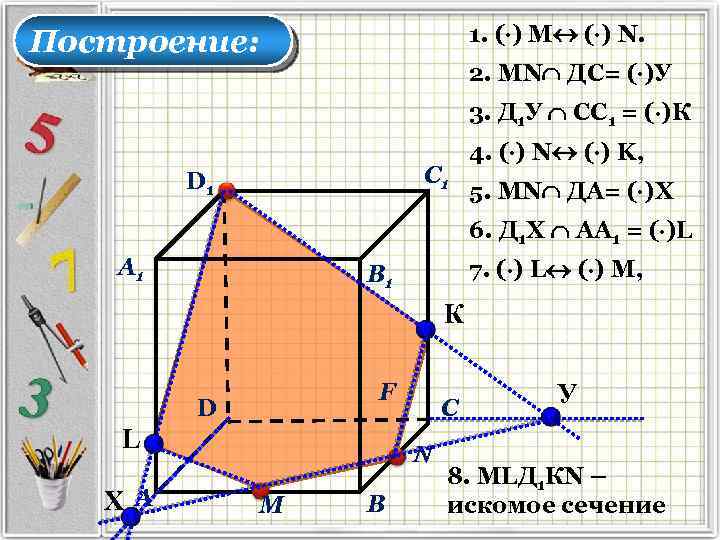
1. ( ) M ( ) N. Построение: 2. МN ДC= ( )У 3. Д 1 У СС 1 = ( )К С 1 D 1 4. ( ) N ( ) K, 5. МN ДА= ( )Х 6. Д 1 Х АА 1 = ( )L А 1 7. ( ) L ( ) М, В 1 К F D L ХА С М В У 8. MLД 1 КN – искомое сечение
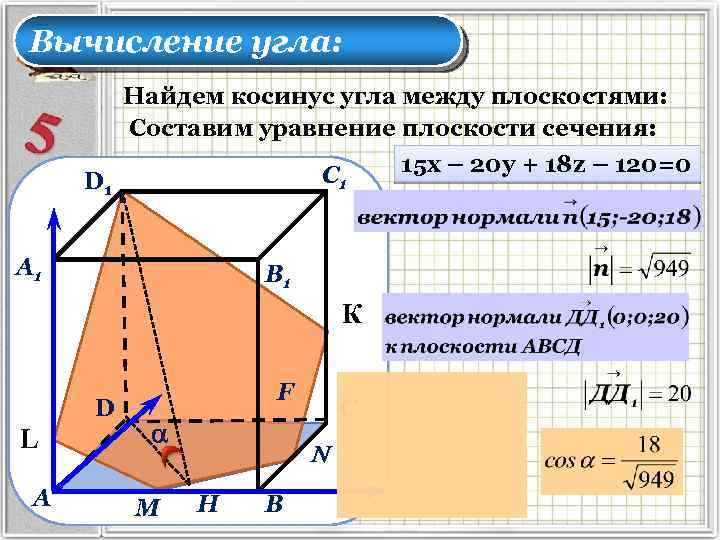
Вычисление угла: Найдем косинус угла между плоскостями: Составим уравнение плоскости сечения: С 1 D 1 А 1 В 1 К D L А F М С Н В 15 х – 20 у + 18 z – 120=0
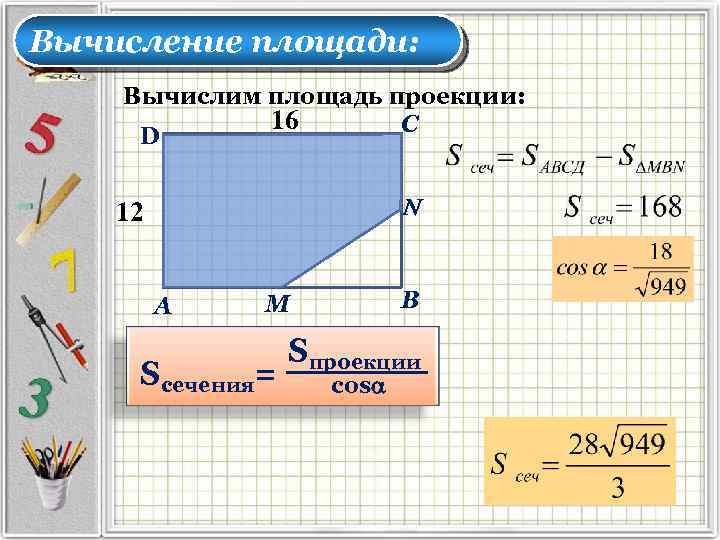
Вычисление площади: Вычислим площадь проекции: 16 С D 12 А В М Sсечения= Sпроекции соs
Скачать презентацию Нахождение площади сечения С 2 Учитель математики МБОУ
С2 нахождение площади сечения.ppt