 Navier Stokes Equations Suppose there is a solution. Given the real number R > 0, determine u, v, w, p(x, y, z, t) — four real functions from four real parameters — such that, letting F = G = H = 0, the 4 × 4 equation system holds: ux + vy + wz = 0 R(uxx + uyy + uzz) + F = ut + px + uxu + uyv + uzw R(vxx + vyy + vzz) + G = vt + py + vxu + vyv + vzw R(wxx + wyy + wzz) + H = wt + pz + wxu + wyv + wzw Speed = Acceleration = Pressure = p 1
Navier Stokes Equations Suppose there is a solution. Given the real number R > 0, determine u, v, w, p(x, y, z, t) — four real functions from four real parameters — such that, letting F = G = H = 0, the 4 × 4 equation system holds: ux + vy + wz = 0 R(uxx + uyy + uzz) + F = ut + px + uxu + uyv + uzw R(vxx + vyy + vzz) + G = vt + py + vxu + vyv + vzw R(wxx + wyy + wzz) + H = wt + pz + wxu + wyv + wzw Speed = Acceleration = Pressure = p 1
 Let’s isolate u from the fourth equation: Now let’s replace u(v, w, p) in (2): 2
Let’s isolate u from the fourth equation: Now let’s replace u(v, w, p) in (2): 2
 (2) implies that: 3
(2) implies that: 3
 (1) implies: Let’s isolate pz: (14) solves an ODE by variation of parameters. 4
(1) implies: Let’s isolate pz: (14) solves an ODE by variation of parameters. 4
![(3) implies: Let’s emphasize p: [see (23)] Let’s replace pz from (18) and py (3) implies: Let’s emphasize p: [see (23)] Let’s replace pz from (18) and py](https://present5.com/presentation/4bcc88f2dc9b23bc5297529316670eb9/image-5.jpg) (3) implies: Let’s emphasize p: [see (23)] Let’s replace pz from (18) and py from (103) Don’t worry: (100 -103) will be explained. 5
(3) implies: Let’s emphasize p: [see (23)] Let’s replace pz from (18) and py from (103) Don’t worry: (100 -103) will be explained. 5
 Let’s derivate on x equation (22) 6
Let’s derivate on x equation (22) 6
 Simplifying: Again, let’s use ODE-Vo. P: Next page, we’re going to replace v(w) on (103). 7
Simplifying: Again, let’s use ODE-Vo. P: Next page, we’re going to replace v(w) on (103). 7
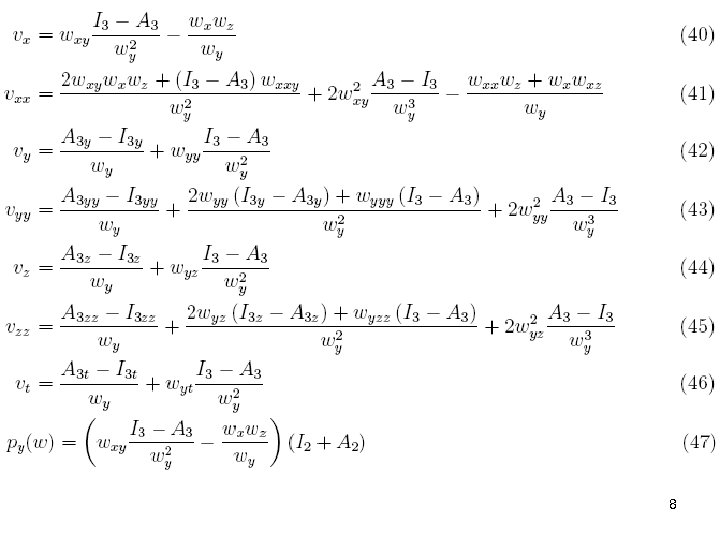 8
8
 Now let’s join (18) and (103), setting pzy = pyz: Well done. This is the first Integral Equation on w. From v(w), the three integrals I 1, I 2 and I 3 x(w) = wxwz become: 9
Now let’s join (18) and (103), setting pzy = pyz: Well done. This is the first Integral Equation on w. From v(w), the three integrals I 1, I 2 and I 3 x(w) = wxwz become: 9
 10
10
 The second integral equation comes from (12): 11
The second integral equation comes from (12): 11
![(97) implies the third 2 -paged Int. Eq. on w. [1/2] 12 (97) implies the third 2 -paged Int. Eq. on w. [1/2] 12](https://present5.com/presentation/4bcc88f2dc9b23bc5297529316670eb9/image-12.jpg) (97) implies the third 2 -paged Int. Eq. on w. [1/2] 12
(97) implies the third 2 -paged Int. Eq. on w. [1/2] 12
![(97) implies the third 2 -paged Int. Eq. on w. [2/2] 13 (97) implies the third 2 -paged Int. Eq. on w. [2/2] 13](https://present5.com/presentation/4bcc88f2dc9b23bc5297529316670eb9/image-13.jpg) (97) implies the third 2 -paged Int. Eq. on w. [2/2] 13
(97) implies the third 2 -paged Int. Eq. on w. [2/2] 13
 Finally, let’s explain equations > (86), by analogy. 14
Finally, let’s explain equations > (86), by analogy. 14
 Thanks. boralaemcasa@gmail. com https: //sites. google. com/site/mathspirituality/ This was a help for Stoke. Nav. pdf 15
Thanks. boralaemcasa@gmail. com https: //sites. google. com/site/mathspirituality/ This was a help for Stoke. Nav. pdf 15
 Map (1), (4) ==> (13) v, w, p ==> (14) pz(v, w) ==> (18) pz(v, w) (15) is part of (18) (2), (4) ==> (12) v, w, p (3), (4) ==> (19) v, w, p ==> (20) (1) <==> (87) (2) <==> (88) (3), vx 0 ==> (89) u(v, w, p) (88), (89) ==> (97) v, w, p (87), (89) ==> (98) v, w, p ==> (99) py(v, w) ==> (103) py(v, w) (100) is part of (103) (91), wx 0 ==> (4) u(v, w, p) (18), (103), (20), vx 0 ==> (21) v, w ==> (22) ==> (26) ==> (27) ==> (34) ==> (35) ==> (36) ==> (37), wy 0 ==> (38) ==> (39) v(w) (39), (103) ==> (47) py(w) (15), v(w) ==> (51) I 1(w) (100), v(w) ==> (60) I 2(w) (18), (103), pzy = pyz ==> (48) w (12), v(w), p(w) ==> (76) w (97), v(w), p(w) ==> (86) w 16
Map (1), (4) ==> (13) v, w, p ==> (14) pz(v, w) ==> (18) pz(v, w) (15) is part of (18) (2), (4) ==> (12) v, w, p (3), (4) ==> (19) v, w, p ==> (20) (1) <==> (87) (2) <==> (88) (3), vx 0 ==> (89) u(v, w, p) (88), (89) ==> (97) v, w, p (87), (89) ==> (98) v, w, p ==> (99) py(v, w) ==> (103) py(v, w) (100) is part of (103) (91), wx 0 ==> (4) u(v, w, p) (18), (103), (20), vx 0 ==> (21) v, w ==> (22) ==> (26) ==> (27) ==> (34) ==> (35) ==> (36) ==> (37), wy 0 ==> (38) ==> (39) v(w) (39), (103) ==> (47) py(w) (15), v(w) ==> (51) I 1(w) (100), v(w) ==> (60) I 2(w) (18), (103), pzy = pyz ==> (48) w (12), v(w), p(w) ==> (76) w (97), v(w), p(w) ==> (86) w 16