Навье-Стокс теңдеуі Энергия теңдеуі
ЛЕКЦИЯ 4 ҚАБАТТАС АҒЫС y x Қабаттас ағыстар - бұл сұйықтың немесе газдың ортада қозғалысы, сұйықтың немесе газдың бір – біріне қатысты параллель қабатпен қозғалуы. Бұл кезде жылдамдықтың тек бір құраушысы сақталады, қалған екеуі нөлге тең: z Тұрақты қасиеттері бар сығылмайтын тұтқыр сұйықтың стационар ағысын қарастырайық Стационар қозғалыс: Сығылмайтын сұйық: Сұйық тұрақты қасиетке ие: Энергия көзі жоқ: Көлемдік күш жоқ: q. N = 0 Fi = 0
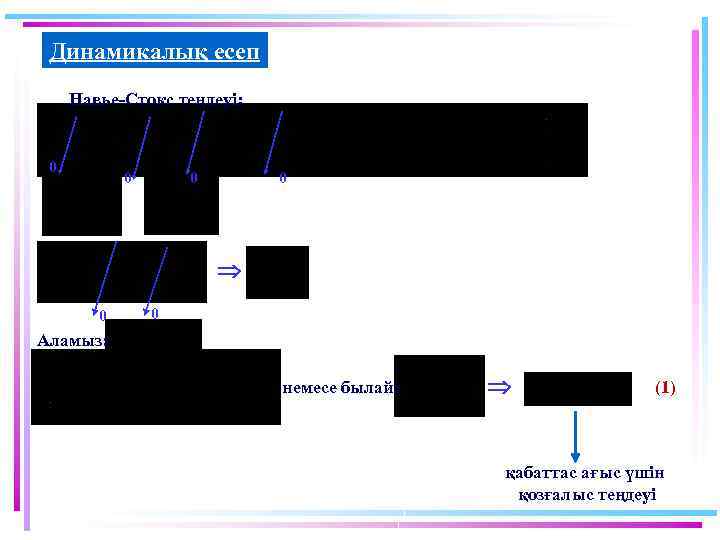
Динамикалық есеп Навье-Стокс теңдеуі: 0 0 Аламыз: немесе былай: (1) қабаттас ағыс үшін қозғалыс теңдеуі
Жылулық есеп Энергия теңдеуінің дивергенттік түрі: (2) grad Т үлкен емес болсын μ = const, ρ = const Өзгертулер енгіземіз: Үзіліссіздік теңдеуінен , онда Ағыс параллель болғандықтан, онда 0 0 0
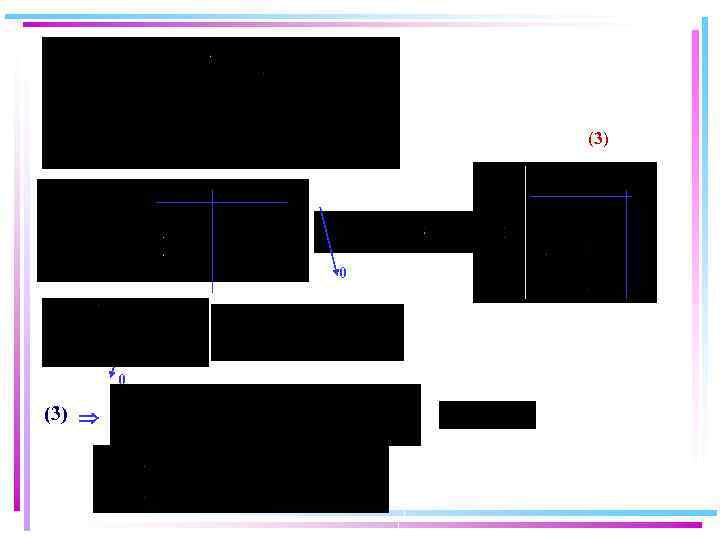
(3) 0 0 (3)
- Қабаттас ағыс үшін энергия теңдеуі
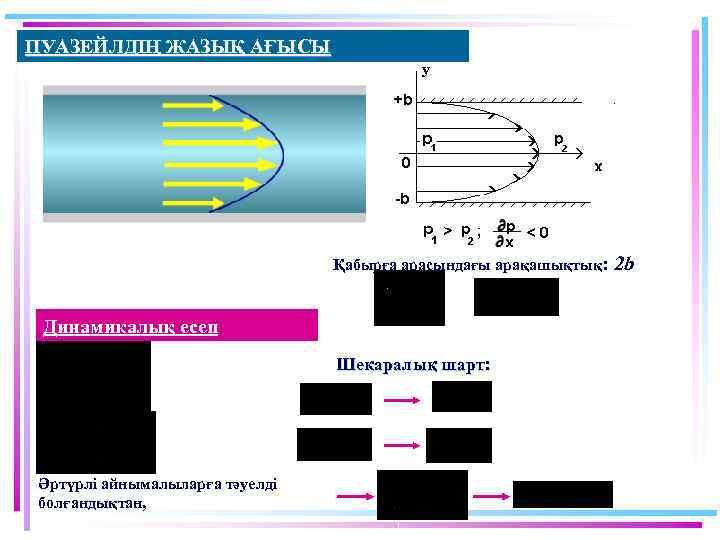
ПУАЗЕЙЛДІҢ ЖАЗЫҚ АҒЫСЫ y Қабырға арасындағы арақашықтық: Динамикалық есеп Шекаралық шарт: Әртүрлі айнымалыларға тәуелді болғандықтан, 2 b
Қозғалыс теңдеуін интегралдаймыз: Шекаралық шарттан C 1 және C 2 анықтаймыз: y = b; u = 0 (4) y = - b; u = 0 (5) - Пуазейлдің қабаттас ағысы үшін жылдамдық профилі
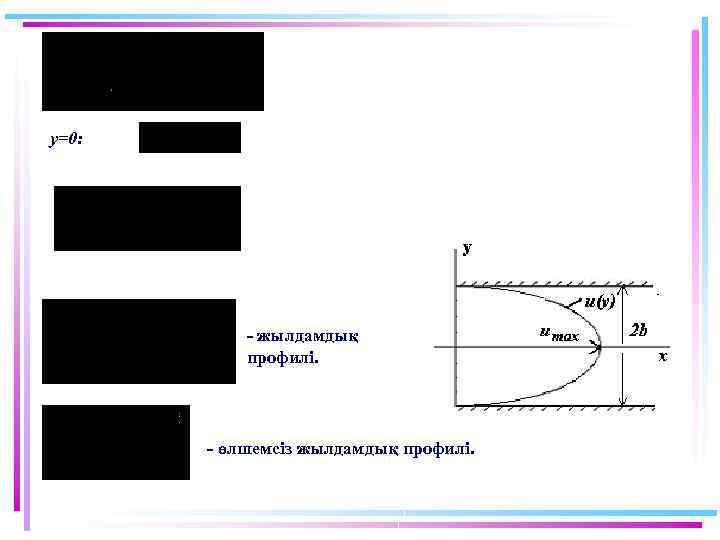
y=0: - жылдамдық профилі. - өлшемсіз жылдамдық профилі.
СҰЙЫҚТЫҢ ШЫҒЫНЫ Q: -каналдың көлденең қимасынан бірлік уақытта ағып өтетін сұйықтық мөлшері. . Алынған шешім кез – келген Re < Reкр үшін орынды Reкр =2300.
ОРТАША ЖЫЛДАМДЫҚ uоp Каналдағы орташа ағыс жылдамдығын анықтаймыз:
Соңғы ұзындықтың аймағындағы қысымның өзгерісін табамыз: l - сұйықтың қозғалысына қарсыласу коэффиценті немесе үйкелістің шығын коэффициенті. (-) таңбасы каналдың бойында қысымның азаятынын көрсетеді. - Дарси өрнегі
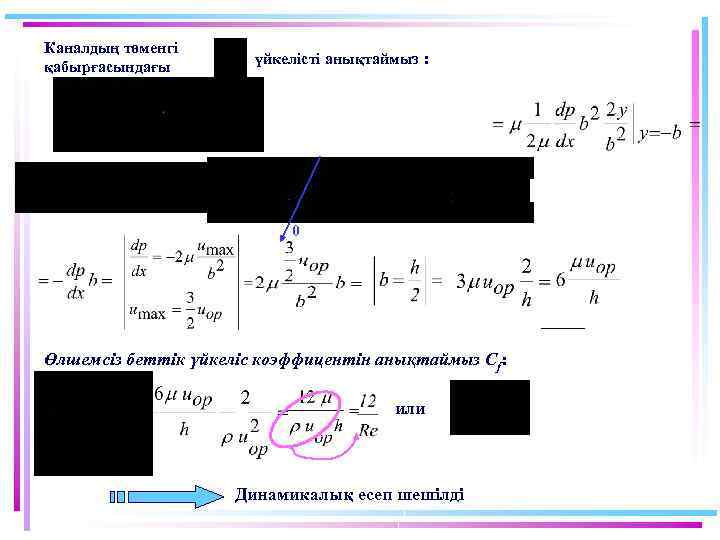
Каналдың төменгі қабырғасындағы үйкелісті анықтаймыз : 0 Өлшемсіз беттік үйкеліс коэффицентін анықтаймыз Cf: или Динамикалық есеп шешілді
Скачать презентацию Навье-Стокс теңдеуі Энергия теңдеуі ЛЕКЦИЯ 4 ҚАБАТТАС
5Слоистые_течен.ppt