Natural Language Semantics using Probabilistic Logic Islam Beltagy

Natural Language Semantics using Probabilistic Logic Islam Beltagy Doctoral Dissertation Proposal Supervising Professors: Raymond J. Mooney, Katrin Erk

• Who is the second president of the US ? – • A: “John Adams” Who is the president that came after the first US president? – A: … 1. Semantic Representation: how the meaning of natural text is represented 2. Inference: how to draw conclusions from that semantic representation 2

Objective • Find a “semantic representation” that is – Expressive – Supports automated inference • Why ? more NLP applications more effectively – Question Answering, Automated Grading, Machine Translation, Summarization … 3

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Future work 4

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Future work 5

Semantic Representations - Formal Semantics • Mapping natural language to some formal language (e. g. first-order logic) [Montague, 1970] • “John is driving a car” x, y, z. john(x) agent(y, x) drive(y) patient(y, z) car(z) • Pros – Deep representation: Relations, Negations, Disjunctions, Quantifiers. . . – Supports automated inference • Cons: Unable to handle uncertain knowledge. Why important ? (pickle, cucumber), (cut, slice) 6

Semantic Representations - Distributional Semantics • Similar words and phrases occur in similar contexts • Use context to represent meaning • Meanings are vectors in high-dimensional spaces • Words and phrases similarity measure – e. g: similarity(“water”, “bathtub”) = cosine(water, bathtub) • Pros: robust probabilistic model that captures graded notion of similarity. • Cons: shallow representation for the semantics 7

Proposed Semantic Representation • Proposed semantic representation: Probabilistic Logic – Combines advantages of: – Formal Semantics (expressive + automated inference) – Distributional Semantics (gradedness) 8

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Future work 9

Probabilistic Logic • Statistical Relational Learning [Getoor and Taskar, 2007] • Combine logical and statistical knowledge • Provide a mechanism for probabilistic inference • Use weighted first-order logic rules – Weighted rules are soft rules (compared to hard logical constraints) – Compactly encode complex probabilistic graphical models • Inference: P(Q|E, KB) • Markov Logic Networks )MLN) [Richardson and Domingos, 2006] • Probabilistic Soft Logic (PSL) [Kimmig et al. , NIPS 2012] 10

Markov Logic Networks [Richardson and Domingos, 2006] x. smoke(x) cancer(x) | 1. 5 x, y. friend(x, y) (smoke(x) smoke(y)) | 1. 1 • Two constants: Anna (A) and Bob (B) Friends(A, A) Cancer(A) Smokes(B) Friends(B, A) Friends(B, B) Cancer(B) • P(Cancer(Anna) | Friends(Anna, Bob), Smokes(Bob)) 11

PSL: Probabilistic Soft Logic [Kimmig et al. , NIPS 2012] • Probabilistic logic framework designed with efficient inference in mind • Atoms have continuous truth values in interval [0, 1] (Boolean atoms in MLN) • Łukasiewicz relaxation of AND, OR, NOT – I(ℓ 1 ℓ 2) = max {0, I(ℓ 1) + I(ℓ 2) – 1} – I(ℓ 1 ℓ 2) = min {1, I(ℓ 1) + I(ℓ 2) } – I( ℓ 1) = 1 – I(ℓ 1) • Inference: linear program (combinatorial counting problem in MLN) 13

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Future work 15

Evaluation Tasks • Two tasks that require deep semantic understanding to do well on them 1) Recognizing Textual Entailment (RTE) [Dagan et al. , 2013] – Given two sentences T and H, finding if T Entails, Contradicts or not related (Neutral) to H – Entailment: T: “A man is walking through the woods. H: “A man is walking through a wooded area. ” – Contradiction: T: “A man is jumping into an empty pool. ” H: “A man is jumping into a full pool. ” – Neutral: T: “A young girl is dancing. ” H: “A young girl is standing on one leg. ” 16

Evaluation Tasks • Two tasks that require deep semantic understanding to do well on them 2) Semantic Textual Similarity (STS) [Agirre et al. , 2012] – Given two sentences S 1, S 2 , judge their semantic similarity on a scale from 1 to 5 – S 1: “A man is playing a guitar. ” S 2: “A woman is playing the guitar. ” (score: 2. 75) – S 1: “A car is parking. ” S 2: “A cat is playing. ” (score: 0. 00) 17

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Future work 18

System Architecture [Beltagy et al. , *SEM 2013] T/S 1 H/S 2 1 Parsing LF 1 LF 2 Knowledge Base 3 Construction KB 2 Task Representation (RTE/STS) One advantage of using logic: Modularity Inference P(Q|E, KB) 4 (MLN/PSL) Result (RTE/STS) 19

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Future work 20

Parsing • Mapping input sentences to logic form • Using Boxer, a rule based system on top of a CCG parser [Bos, 2008] • “John is driving a car” x, y, z. john(x) agent(y, x) drive(y) patient(y, z) car(z) 21

Task Representation [Beltagy et al. , Sem. Eval 2014] • Represent all tasks as inferences of the form: P(Q|E, KB) • RTE – Two inferences: P(H|T, KB), P(H| T, KB) – Use a classifier to map probabilities to RTE class • STS – Two inferences: P(S 1|S 2, KB), P(S 2|S 1, KB) – Use regression to map probabilities to overall similarity score 22

Domain Closure Assumption (DCA) • There are no objects in the universe other than the named constants – Constants need to be explicitly added – Universal quantifiers do not behave as expected because of finite domain – e. g. Tweety is a bird and it flies All birds fly P(Q|E, KB) E Q Skolemization none All birds fly ⇏ Some birds fly Tweety is a bird. It flies All birds fly ( ) none future work 23

P(Q|E, KB) E Q Skolemization none All birds fly ⇏ Some birds fly Tweety is a bird. It flies All birds fly ( ) none future work • E: • Skolemized E: x, y. john(x) agent(y, x) eat(y) john(J) agent(T, J) eat(T) • Embedded existentials – E: x. bird(x) y. agent(y, x) fly(y) – Skolemized E: x. bird(x) agent(f(x), x) fly(f(x)) – Simulate skolem functions x. bird(x) y. skolemf(x, y) agent(y, x) fly(y) – skolemf (B 1, C 1), skolemf (B 2, C 2) … 24

P(Q|E, KB) E Q Skolemization none All birds fly ⇏ Some birds fly Tweety is a bird. It flies All birds fly ( ) none future work • E : x. bird(x) y. agent(y, x) fly(y) • Q: x, y. bird(x) agent(y, x) fly(y) (false) • Solution: introduce additional evidence bird(B) – Pragmatically, birds exist (Existence) • Negated existential – E : x, y. bird(x) agent(y, x) fly(y) – No additional constants needed 25

P(Q|E, KB) E Q Skolemization none All birds fly ⇏ Some birds fly Tweety is a bird. It flies All birds fly ( ) none future work • E : bird( ) agent(F, ) fly (F) • Q: x. bird(x) y. agent(y, x) fly(y) (true) • Universal quantifiers work only on the constants of the given finite domain • Solution: add an extra bird( ) to the domain – If the new bird can be shown to fly, then there is an explicit universal quantification in E 26

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Future work 27

Knowledge Base Construction • Represent background knowledge as weighted inference rules 1) Word. Net rules – Word. Net: lexical database of word and their semantic relations – Synonyms: x. man(x) guy(x) | w = ∞ – Hyponym: x. car(x) vehicle(x) | w = ∞ – Antonyms: x. tall(x) short(x) | w = ∞ 28

Knowledge Base Construction • Represent background knowledge as weighted inference rules 2) Distributional rules (on-the-fly rules) – For all pairs of words )a, b( where a T/S 1, b H/S 2, generate the rule x. a)x (→ b)x( | f(w) – w =cosine(a, b( cos – f(w) = log(w/(1 -w)) x. hamster(x) → gerbil(x) | f(w) 29

Outline • Introduction • Completed research – Parsing and task representation – Knowledge base construction – Inference • RTE using MLNs • STS using PSL – Evaluation • Future work 30

Inference • Inference problem: P(Q|E, KB) • Solve it using MLN and PSL for RTE and STS – RTE using MLNs – STS using PSL 31

Outline • Introduction • Completed research – Parsing and task representation – Knowledge base construction – Inference • RTE using MLNs • STS using PSL – Evaluation • Future work 32

MLNs for RTE - Query Formula (QF) [Beltagy and Mooney, Star. AI 2014] • Alchemy (MLN’s implementation) calculates only probabilities of ground atoms • Inference algorithm supports query formulas – P(Q|R) = Z(Q U R) / Z(R) [Gogate and Domingos, 2011] – Z: normalization constant of the probability distribution – Estimate the partition function Z using Sample. Search [Gogate and Dechter, 2011] – Sample. Search is an algorithm to estimate the partition function Z of mixed graphical models (probabilistic and deterministic) 33

MLNs for RTE - Modified Closed-world (MCW) [Beltagy and Mooney, Star. AI 2014] • MLN’s grounding generates very large graphical models • Q has O(cv) ground clauses – v: number of variables in Q – c: number of constants in the domain 34

MLNs for RTE - Modified Closed-world (MCW) [Beltagy and Mooney, Star. AI 2014] • Low priors: by default, ground atoms have very low probabilities, unless shown otherwise thought inference • Example – E: man(M) agent(D, M) drive(D) – Priors: x. man(x) | -2, x. guy(x) | -2, x. drive(x) | -2 – KB: x. man(x) guy(x) | 1. 8 – Q: x, y. guy(x) agent(y, x) drive(y) – Ground Atoms: man(M), man(D), guy(M), guy(D), drive(M), drive(D) • Solution: a MCW to eliminate unimportant ground atoms – not reachable from the evidence (evidence propagation) – Strict version of low priors – Dramatically reduces size of the problem 35

Outline • Introduction • Completed research – Parsing and task representation – Knowledge base construction – Inference • RTE using MLNs • STS using PSL – Evaluation • Future work 36

MLNs for STS [Beltagy et al. , *SEM 2013] • Strict conjunction in Q does not fit STS – E: “A man is driving”: x, y. man(x) drive(y) agent(y, x) – Q: “A man is driving a bus”: x, y, z. man(x) drive(y) agent(y, x) bus(z) patient(y, z) • Break Q into mini-clauses then combine their evidences using an averaging combiner [Natarajan et al. , 2010] x, y, z. man(x) agent(y, x) result(x, y, z) | w x, y, z. drive(y) patient(y, z) result(x, y, z) | w x, y, z. bus(z) patient(y, z) result(x, y, z) | w 37

Outline • Introduction • Completed research – Parsing and task representation – Knowledge base construction – Inference • RTE using MLNs • STS using PSL – Evaluation • Future work 38

PSL for STS [Beltagy and Erk and Mooney, ACL 2014] • Similar to MLN, conjunction in PSL does not fit STS • Replace conjunctions in Q with average – I(ℓ 1 … ℓn) = avg( I(ℓ 1), …, I(ℓn)) • Inference – “average” is a linear function – No changes in the optimization problem – Heuristic grounding (details omitted) 39

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Knowledge Base • Inference • Future work 40

Evaluation -Datasets • SICK (RTE and STS) [Sem. Eval 2014] – “Sentences Involving Compositional Knowledge” – 10, 000 pairs of sentences • msr-vid (STS) [Sem. Eval 2012] – Microsoft video description corpus – 1, 500 pair of short video descriptions • msr-par (STS) [Sem. Eval 2012] – Microsoft paraphrase corpus – 1, 500 pair of long news sentences 41

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Knowledge Base • Inference • Future work 42

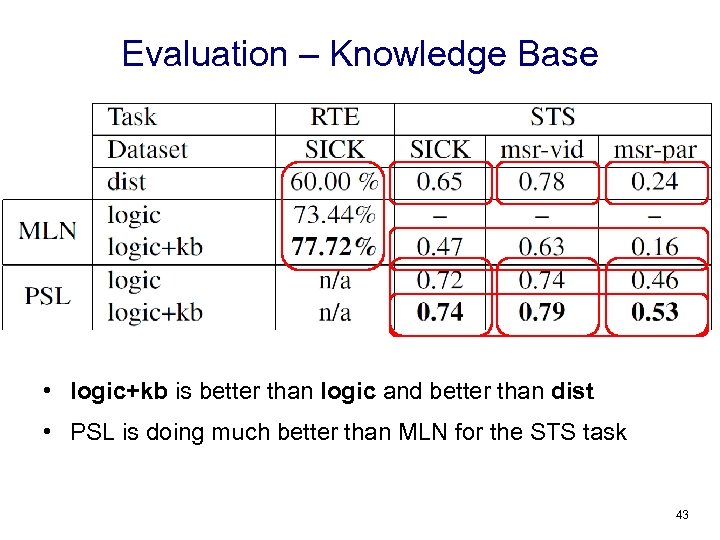
Evaluation – Knowledge Base • logic+kb is better than logic and better than dist • PSL is doing much better than MLN for the STS task 43

Evaluation – Error analysis of RTE • Our system’s accuracy: 77. 72% • The remaining 22. 28% are – Entailment pairs classified as Neutral: 15. 32% – Contradiction pairs classified as Neutral: 6. 12% – Other: 0. 84 % • System precision: 98. 9%, recall: 78. 56%. – High precision, low recall is the typical behavior of logic-base systems • Fixes (future work) – Larger knowledge base – Fix some limitations in the detection of contradictions 44

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Knowledge Base • Inference • Future work 45

Evaluation – Inference (RTE) [Beltagy and Mooney, Star. AI 2014] • Dataset: SICK (from Sem. Eval 2014) • Systems compared – mln: using Alchemy out-of-the-box – mln+qf: our algorithm to calculate probability of query formula – mln+mcw: mln with our modified-closed-world – mln+qf+mcw: both components System Accuracy CPU Timeouts(30 min) mln 57% 2 min 27 sec 96% mln+qf 69% 1 min 51 sec 30% mln+mcw 66% 10 sec 2. 5% mln+qf+mcw 72% 7 sec 2. 1% 46

Evaluation – Inference (STS) [Beltagy and Erk and Mooney, ACL 2014] • Compare MLN with PSL on the STS task PSL time MLN timeouts (10 min) msr-vid 8 s 1 m 31 s 9% msr-par 30 s 11 m 49 s 97% SICK 10 s 4 m 24 s 36% • Apply MCW to MLN for a fairer comparison because PSL already has a lazy grounding 47

Outline • Introduction – Semantic representations – Probabilistic logic – Evaluation tasks • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Future work – Short Term – Long Term 48

Future Work – RTE Task formulation 1) Better detecting of contradictions – Example where the current P(H| T) fails • T: “No man is playing a flute” • H: “A man is playing a large flute” – Detection of contradiction is • T H false (from the logic point of view) • T H probabilistic P( H|T) = 1 – P(H|T) (useless) • H T probabilistic P( T|H) 49

Future Work – RTE Task formulation 2) Using ratios – P(H|T) / P(H) – P( T|H) / P( T) 50

P(Q|E, KB) E Q Skolemization none All birds fly ⇏ Some birds fly Tweety is a bird. It flies All birds fly ( ) none Future Work: DCA • Q : x, y. bird(x) agent(y, x) fly(y) • Because of closed-world, Q comes true regardless of E • Need Q to be true only when Q is explicitly stated in E • Solution – Add the negation of Q to the MLN with high weight not infinity – R: bird(B) agent(F, B) fly(F) | w=5 – P (Q|R) = 0 – P(Q|E, R) = 0 unless E is negating R 51

Future Work – Knowledge Base Construction 1) Precompiled rules of paraphrase collections like PPDB [Ganitkevitch et al. , NAACL 2013] – e. g: “solves => finds a solution to” e, x. solve(e) patient(e, x) s. find(e) patient(e, s) solution(s) to(t, x) | w – Variable binding is not trivial • Templates • Difference between logical expressions of the sentence with and without the rule applied 52

Future Work – Knowledge Base Construction 2) Phrasal distributional rules – Use linguistically motivated templates like • Noun-phrase => noun-phrase x. little(x) kid(x) smart(x) boy(x) | w • Subject-verb-object => subject-verb-object x, y, z. man(x) agent(y, x) drive(y) patient(y, z) car(z) guy(x) agent(y, x) ride(y) patient(y, z) bike(z) | w 53

Future Work – Inference 1) Better MLN inference with query formula – Currently, we estimate Z(K U R) and Z(R) – Combine both runs in one that exploits • Similarities between Q U R and R • We only need the ratio, not the absolute values 54

Future Work – Inference 2) Generalized modified closed-world assumption – It is not clear how to propagate evidence of rule like x. dead(x) live(x) – MCW needs to be generalized to arbitrary MLNs – Find and eliminate ground atoms that have: marginal probability = prior probability 55

Future Work – Weight Learning • One of the following – Weight learning for inference rules • Learn a better mapping from the weights we have on resources to MLN weights • Learning how to weight different rules of different resources differently – Weight learning for the STS task • Weight different parts of the sentence differently • e. g. “black dog” is more similar to “white dog” that “black cat” 56

Outline • Introduction • Completed research – Parsing and task representation – Knowledge base construction – Inference – Evaluation • Future work – Short Term – Long Term 57

Long-term Future Work 1) Question Answering – Our semantic representation is a general and expressive one, so apply it to more tasks – Given a query, find an answer for it from large corpus of unstructured text – Inference finds best filling for existentially quantified query – Efficient inference is the bottleneck 2) Generalized Quantifiers – Few, most, many, … are not natively supported in first-order logic – Add support for them using • Checking monotonicity • Represent Few and Most as weighted universally quantified rules 58

Long-term Future Work 3) Contextualize Word. Net Rules – Use Word Sense Disambiguation, then generate weighted inference rules from Word. Net 4) Other Languages – Theoretically, this is a language independent semantic representation – Practically, resources are not available especially CCGBanks to train parsers and Boxer 5) Inference Inspector – Visualize the inference process and highlight most effective rules – Not trivial in MLN because all rules affect the final result to some extent 59

Conclusion • Probabilistic logic for semantic representation – – – expressivity, automated inference and gradedness Evaluation on RTE and STS Formulating tasks as probabilistic logic inferences Building a knowledge base Performing inference efficiently base on the task • For the short term future work, we – enhance formulation of the RTE task, build bigger knowledge base from more resources, generalize the modified closed-world assumption, enhance our MLN inference algorithm, and use some weight learning • For the long term future work, we – apply our semantic representation to the question answering task, support generalized quantifiers, contextualize Word. Net rules, apply our semantic representation to other languages and implementing a probabilistic logic inference inspector 60

Thank You