National Research Nuclear University MEPh I Department Elementary

National Research Nuclear University «MEPh. I» Department «Elementary Particle Physics» INSTRUMENTS and FACILITY in HIGH ENERGY PHYSICS Dr B. A. Chernyshev Part 2 Interactions of Particles with Matter Lection 10 Leptons and Photons

Electromagnetic Interactions of Particles with Matter

Stopping Power (-d. E/dx) for Muons

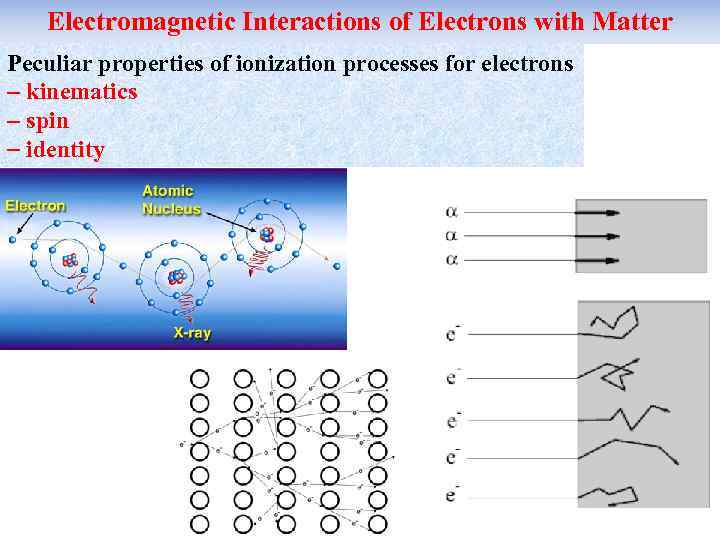Electromagnetic Interactions of Electrons with Matter Peculiar properties of ionization processes for electrons kinematics spin identity

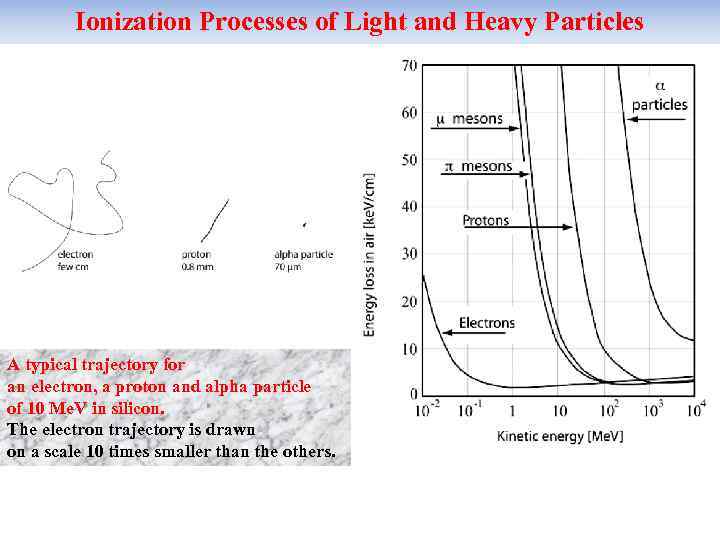Ionization Processes of Light and Heavy Particles A typical trajectory for an electron, a proton and alpha particle of 10 Me. V in silicon. The electron trajectory is drawn on a scale 10 times smaller than the others.

Stopping Power (-d. E/dx) for Electrons ionization losses radiation losses

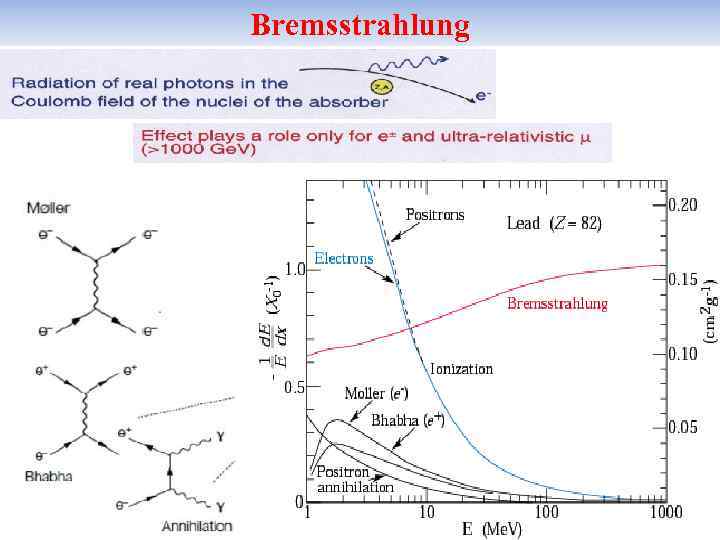Bremsstrahlung

Energy Loss Bremsstrahlung Е << meс2 1<< Е/meс2 <<137/Z 1/3 Е/meс2 >>137/Z 1/3

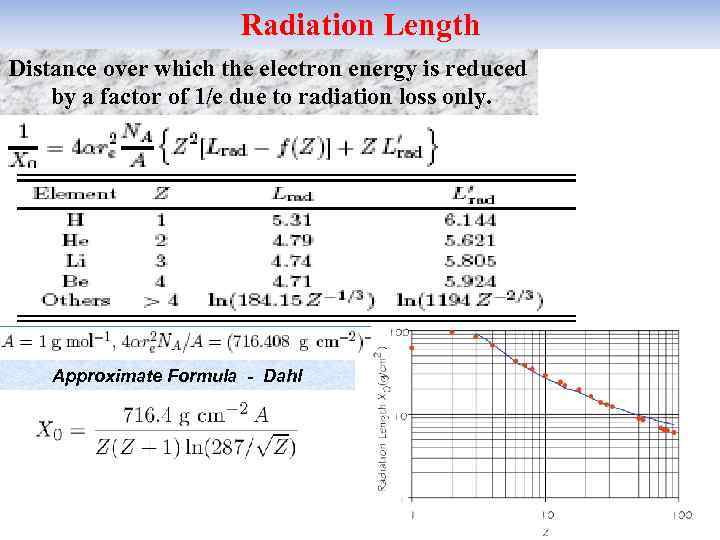Radiation Length Distance over which the electron energy is reduced by a factor of 1/e due to radiation loss only. Approximate Formula - Dahl

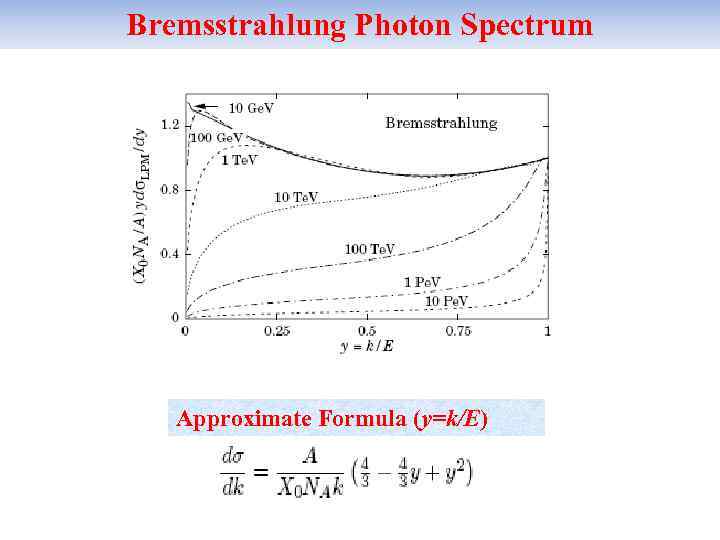Bremsstrahlung Photon Spectrum Approximate Formula (y=k/E)

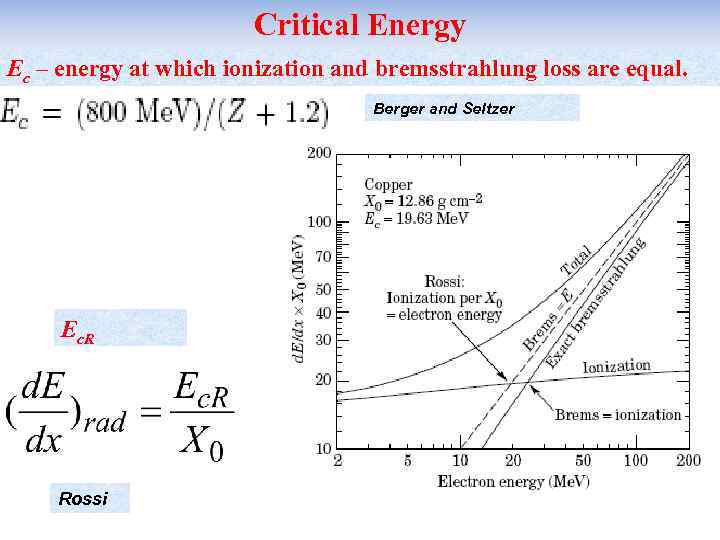Critical Energy Ec – energy at which ionization and bremsstrahlung loss are equal. Berger and Seltzer Ec. R Rossi

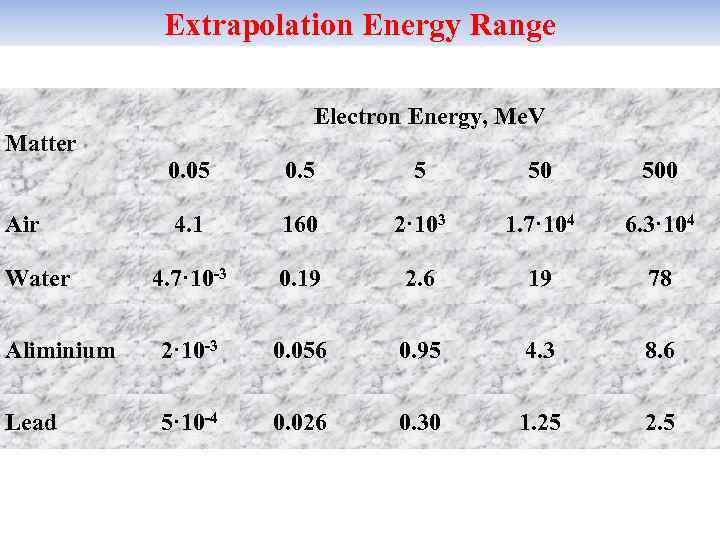Extrapolation Energy Range Electron Energy, Me. V Matter 0. 05 0. 5 5 50 500 4. 1 160 2· 103 1. 7· 104 6. 3· 104 4. 7· 10 -3 0. 19 2. 6 19 78 Aliminium 2· 10 -3 0. 056 0. 95 4. 3 8. 6 Lead 5· 10 -4 0. 026 0. 30 1. 25 2. 5 Air Water

Positron Interaction with Matter Interaction of positrons in matter is described by the same relations as for electrons, but additionally taken into account annihilation effects Cross section ~ Z/ + at + << c, ~ Z/E+ at E+ >> me; “Time-Life" of the slow positron in a solid ~ 10 -10 с.

Electromagnetic Wave Scale 13. 6 e. V Range Wave Length Energy Radiowave Infrared radiation > 1 mm 760 nm ÷ 1 mm < 1. 2 me. V ÷ 1. 6 e. V Visible light Ultraviolet X-rays γ-quanta 380 nm ÷ 760 nm 120 Å ÷ 380 nm 0. 012 Å ÷ 120 Å < 0. 012 Å 1. 6 e. V ÷ 3. 2 e. V ÷ 100 e. V ÷ 1 Me. V > 1 Me. V

Photon Interaction with Matter Three basic processes of photon interaction with matter : - photoeffect; - Compton effect; - electron-positron pair production.

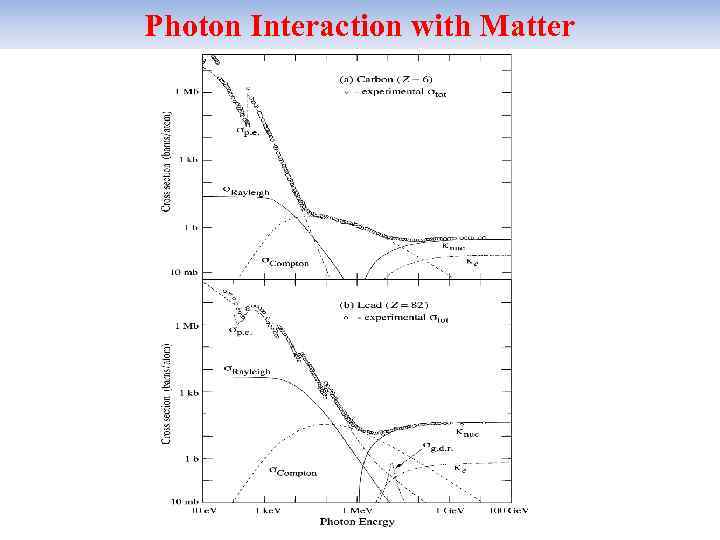Photon Interaction with Matter

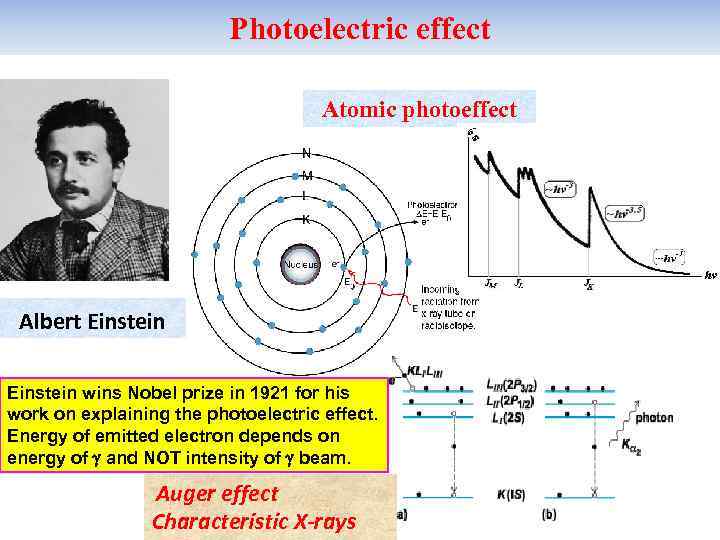Photoelectric effect Atomic photoeffect Albert Einstein wins Nobel prize in 1921 for his work on explaining the photoelectric effect. Energy of emitted electron depends on energy of and NOT intensity of beam. Auger effect Characteristic X-rays

Theory of Atomic Photoeffect Nonrelativistic case (E << mec 2): n = P/P; e – photon polarization vector mec 2 >> E >> I (η << 1): Ultrarelativistic case (E -I >> mec 2): Total cross section

The Main Conclusions of the Photoeffect Theory Cross section ~ Z 5; Cross section decreases with increasing energy E : ~ (1/E )7/2, at E > IK; ~ 1/E , at E >> IK; Contribution of the K shell to cross section is ~ 80%.

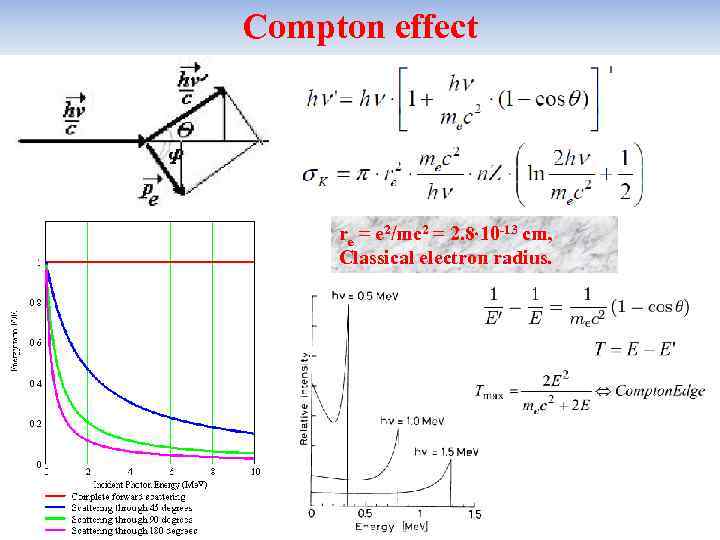Compton effect re = e 2/mc 2 = 2. 8 10 -13 cm, Classical electron radius.

The Main Properties of the Compton Scattering • Cross section ~ Z (incoherent sum of the contributions of atomic electrons); • Cross section decreases with increasing energy E : ≈ σT, at E << mec 2; ~ ln(E )/E , at E >> mec 2; • Nuclear contribution in cross section is very small, Classical nuclear radius rn = Z 2 e 2/(Mnc 2) ~ 10 -3 -10 -4 re.

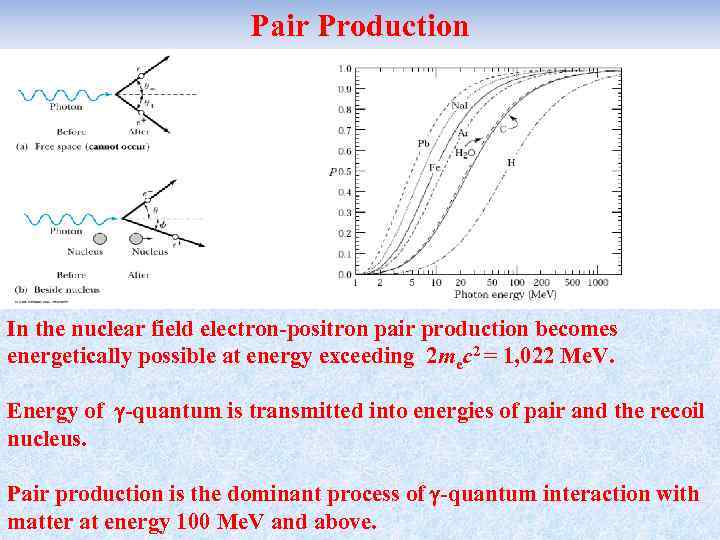Pair Production In the nuclear field electron-positron pair production becomes energetically possible at energy exceeding 2 mec 2 = 1, 022 Me. V. Energy of -quantum is transmitted into energies of pair and the recoil nucleus. Pair production is the dominant process of -quantum interaction with matter at energy 100 Me. V and above.

Pair Production Threshold Energy Pair Production in the frames of QED theory Probability of the Process

Pair Production Cross Section Nonrelativistic case (0 < E - 2 mec 2 << mec 2) Electron and positron momenta are predominantly perpendicular to -momentim Ultrarelativistic case (E >> mec 2) Electron and positron are flying in the direction of - quantum angle ~ me c 2 / E

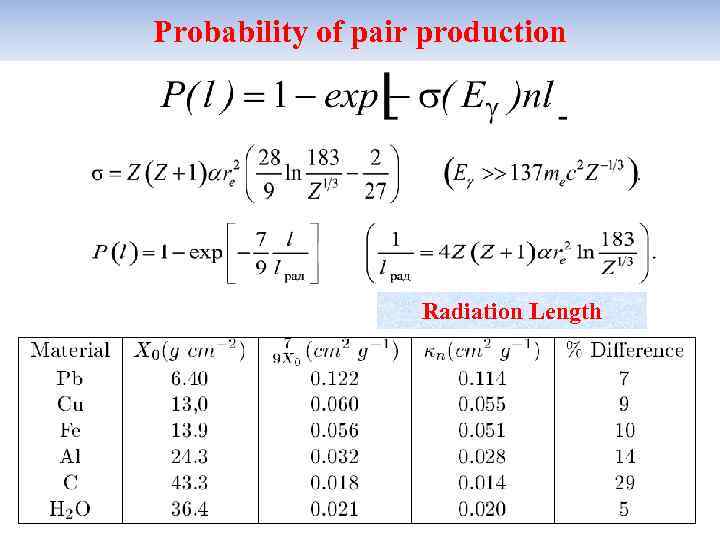Probability of pair production Radiation Length

Linear energy-absorption coefficient [cm-1]: Mass energy-absorption coefficient μ [cm 2/g]

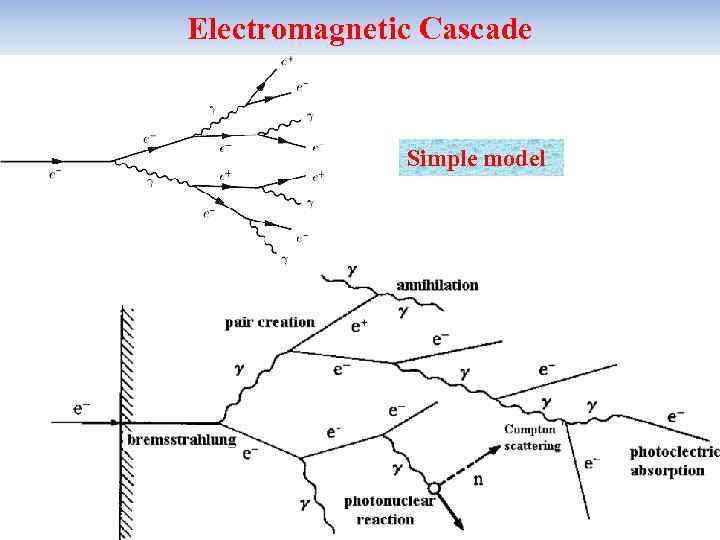Electromagnetic Cascade Simple model

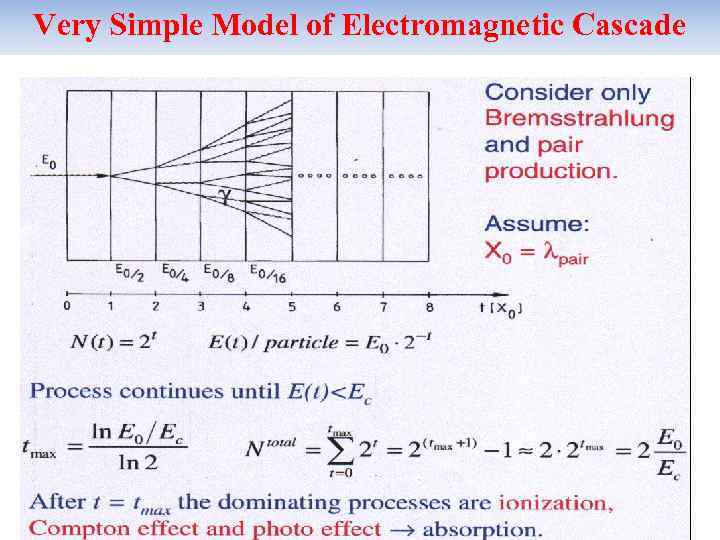Very Simple Model of Electromagnetic Cascade

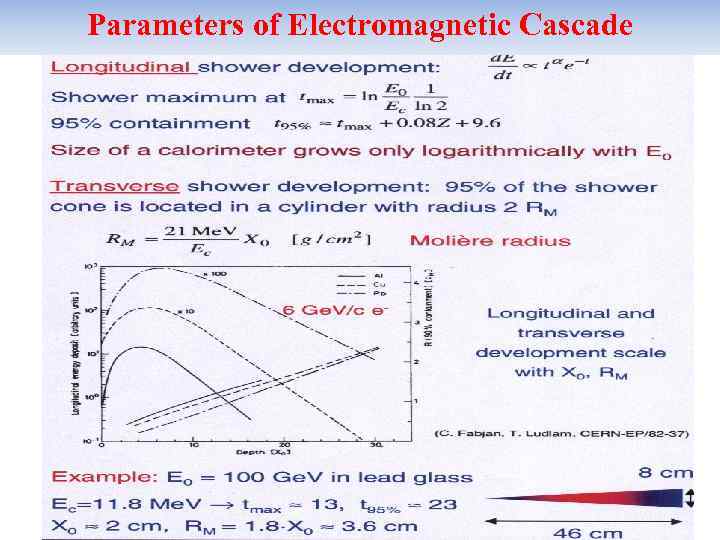Parameters of Electromagnetic Cascade

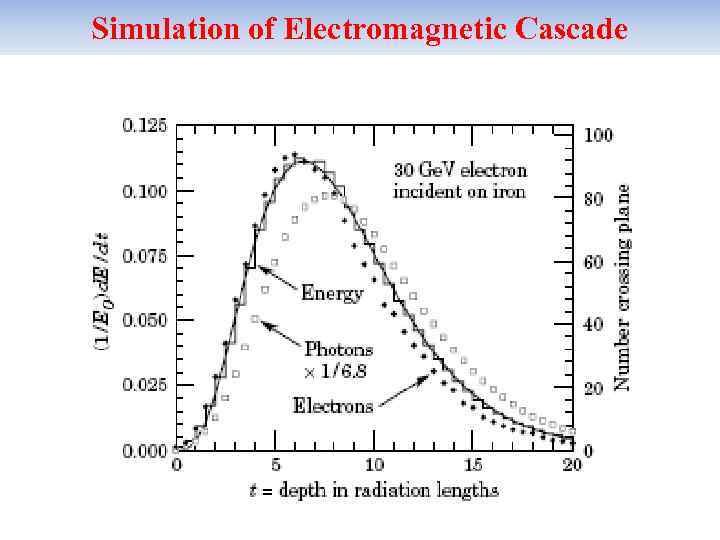Simulation of Electromagnetic Cascade

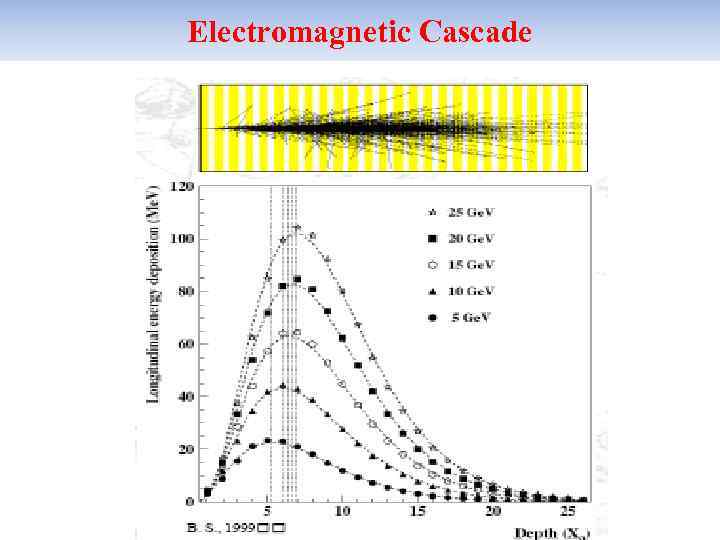Electromagnetic Cascade

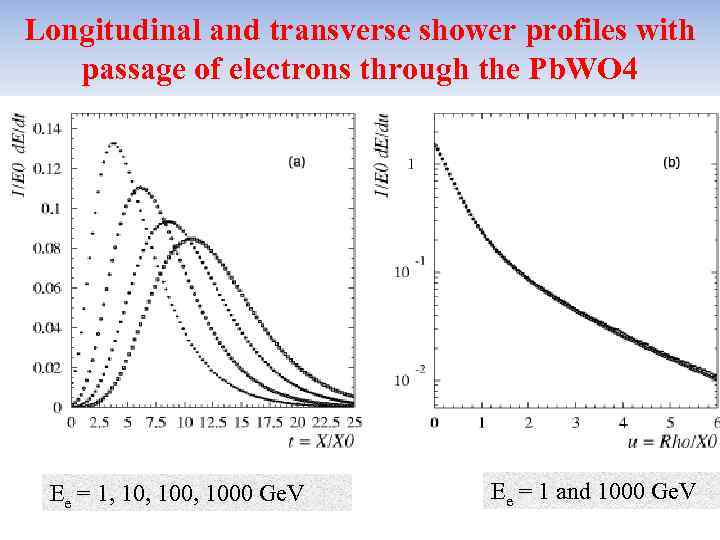Longitudinal and transverse shower profiles with passage of electrons through the Pb. WO 4 Ee = 1, 100, 1000 Ge. V Ee = 1 and 1000 Ge. V