National Central University Department of Mathematics Numerical Electro

National Central University Department of Mathematics Numerical Electro. Magnetics & Semiconductor Industrial Applications 10 Summary: RC extractor & Electro. Magnetic (EM) field solver Ke-Ying Su Ph. D.

Contents (1) Design flow & EDA tools • Methods in Raphael 2 D & 3 D, QRC, Peak. View, Momentum, & EMX. (2) Quasi-static-analyses (C extraction) • • • corss-section profile vs Green's function process variation vs method of moment 2 D & 3 D models in a RC techfile (3) PEEC (RLK extraction) • • Partial-Element-Equivalent-Circuit (PEEC) RLK relations in spiral inductors and interconnects (4) Full-wave analyses (S-parameter extraction) • • Maxwell's equations S-parameters from current waves (5) Double Patterning Technology & Solution P. 1 Ke-Ying. Su Ph. D.

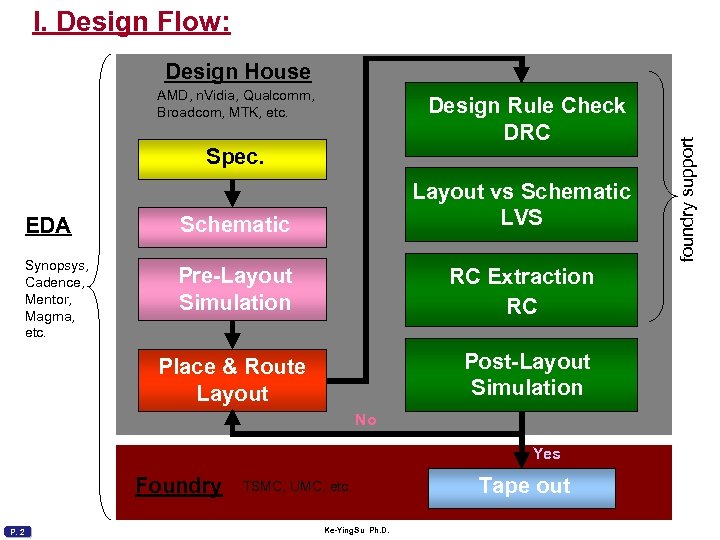I. Design Flow: AMD, n. Vidia, Qualcomm, Broadcom, MTK, etc. Design Rule Check DRC Spec. EDA Schematic Layout vs Schematic LVS Synopsys, Cadence, Mentor, Magma, etc. Pre-Layout Simulation RC Extraction RC Place & Route Layout Post-Layout Simulation No Yes Foundry P. 2 TSMC, UMC, etc. Ke-Ying. Su Ph. D. Tape out foundry support Design House

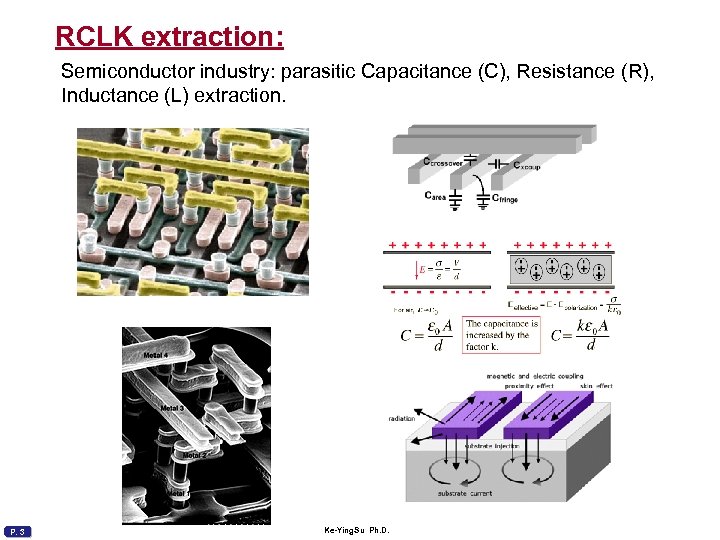RCLK extraction: Semiconductor industry: parasitic Capacitance (C), Resistance (R), Inductance (L) extraction. P. 3 Ke-Ying. Su Ph. D.

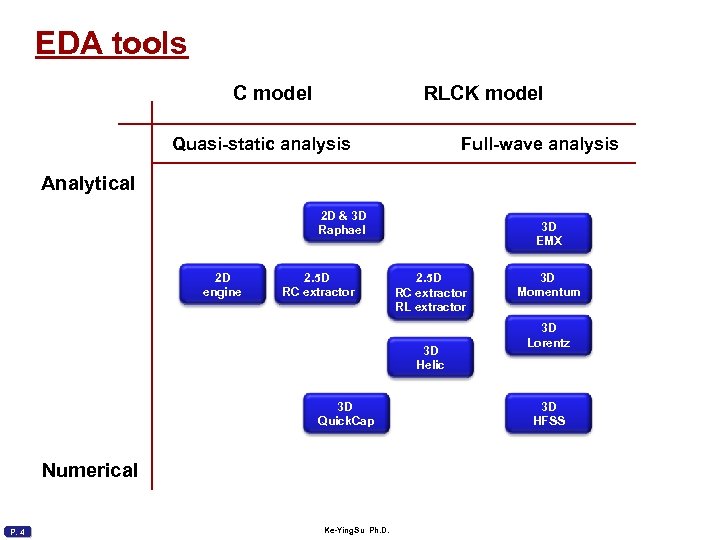EDA tools C model RLCK model Quasi-static analysis Full-wave analysis Analytical 2 D & 3 D Raphael 2 D engine 2. 5 D RC extractor 3 D EMX 2. 5 D RC extractor RL extractor 3 D Helic 3 D Quick. Cap Numerical P. 4 Ke-Ying. Su Ph. D. 3 D Momentum 3 D Lorentz 3 D HFSS

3 D Momentum 3 D EMX • integral equation in frequency domain • Method of moment • Galerkin’s procedure • microwave full wave mode • faster RF quasi-static mode 3 D Lorentz QRC RC extractor RL extractor • Partial Element Equivalent Circuit (PEEC) for RLCK extraction 2 D & 3 D Raphael • Mixed potential integral equation • Partial Element Equivalent Circuit (PEEC) 3 D Quick. Cap • Boundary element method (BEM) • Finite difference Method (FD) P. 5 • Laplace’s equation • Floating random walk method Ke-Ying. Su Ph. D.

II. Quasi-static analyses (2 D & 3 D) Cross-section of a dielectric layer 1. Laplace’s equation 2. Spectral potential function of a charge Cross-section of multi-dielectric layers 3. Matrix pencil method 4. Spectral potential function of a charge “Complex images for electrostatic field computation in multilayered media, ” Y. L. Chow, J. J. Yang, G. E. Howard, IEEE MTT vol. 39, no. 7, July 1991, pp. 1120 -1125. “A multipipe model of general strip transmission lines for rapid convergence of integral equation singularities, ” G. E. Howard, J. J. Yang, Y. L. Chow, IEEE MTT vol. 40, no. 4, April 1992, pp. 628 -636. P. 6 Ke-Ying. Su Ph. D. A given cross-section profile is related to a Green’s function.

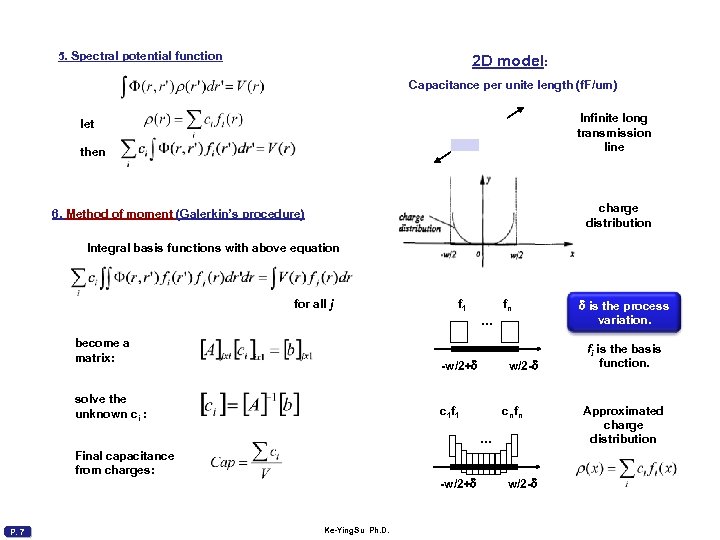5. Spectral potential function 2 D model: Capacitance per unite length (f. F/um) Infinite long transmission line let then charge distribution 6. Method of moment (Galerkin’s procedure) Integral basis functions with above equation for all j f 1 fn … become a matrix: -w/2+d solve the unknown ci : w/2 -d c 1 f 1 cnfn … Final capacitance from charges: -w/2+d P. 7 Ke-Ying. Su Ph. D. w/2 -d d is the process variation. fi is the basis function. Approximated charge distribution

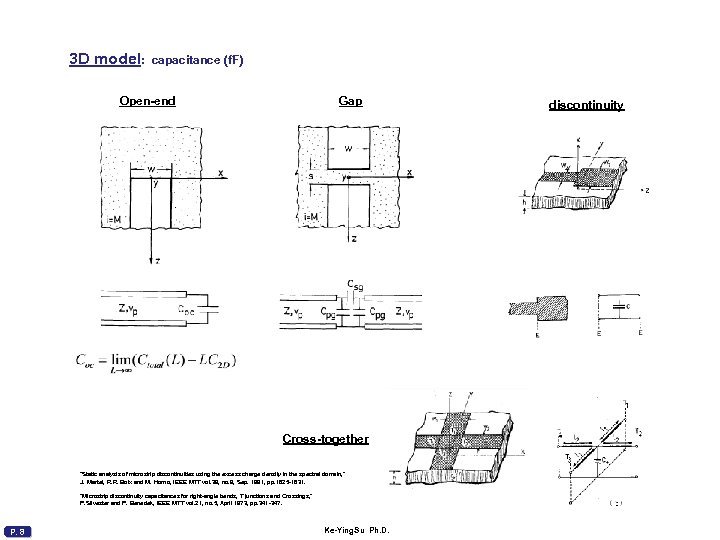3 D model: capacitance (f. F) Open-end Gap Cross-together “Static analysis of microstrip discontinuities using the excess charge density in the spectral domain, ” J. Martel, R. R. Boix and M. Horno, IEEE MTT vol. 39, no. 9, Sep. 1991, pp. 1625 -1631. “Microstrip discontinuity capacitances for right-angle bends, T junctions and Crossings, ” P. Silvester and P. Benedek, IEEE MTT vol. 21, no. 5, April 1973, pp. 341 -347. P. 8 Ke-Ying. Su Ph. D. discontinuity

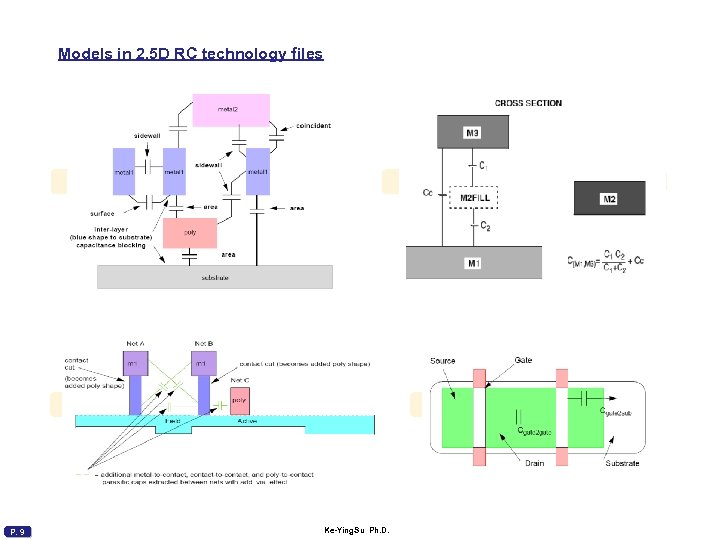Models in 2. 5 D RC technology files P. 9 Ke-Ying. Su Ph. D.

III. Partial Element Equivalent Circuit (PEEC) 1972, Albert E. Ruehli (IBM) to solve interconnect problems on packages. IEEE MTT, vol. 42, no. 9, Sep. 1994, pp. 1750 -1758 Project: IBM & MIT Integral equation from Maxwell’s equations Assume Let where Ii is the current inside filament i. Ii is a unit vector along the length of a filament wi(r) is the basis function of filament i. P. 10 Filaments in a conductor for skin and proximity effects. Ke-Ying. Su Ph. D.

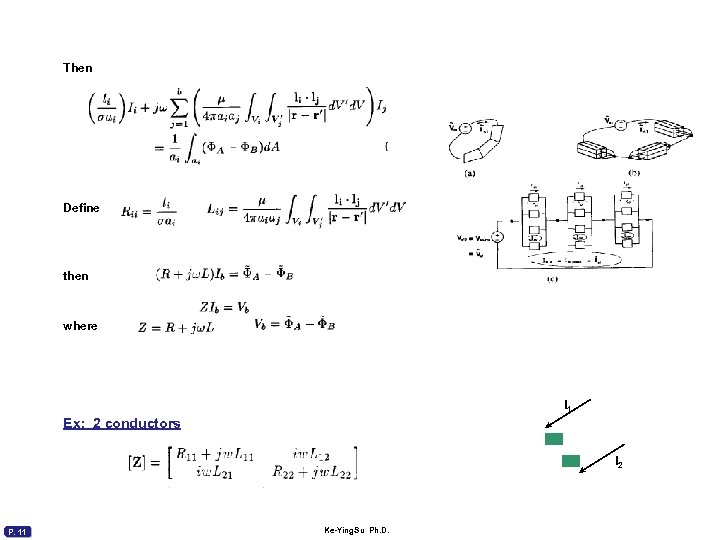Then Define then where l 1 Ex: 2 conductors l 2 P. 11 Ke-Ying. Su Ph. D.

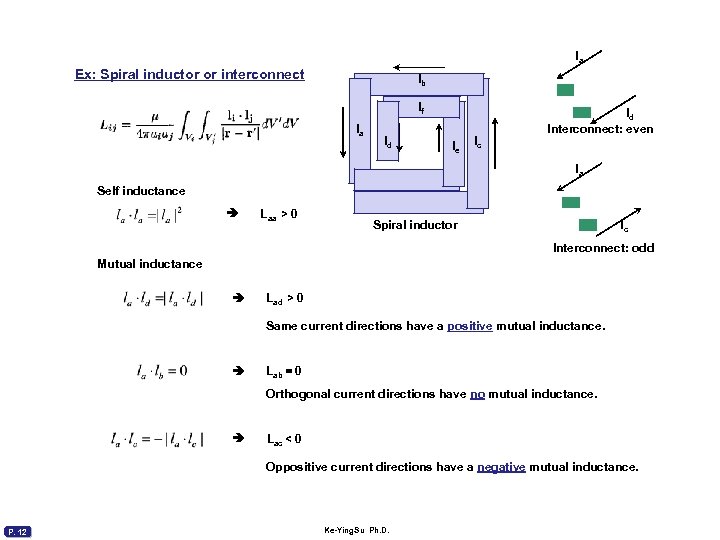la Ex: Spiral inductor or interconnect lb lf la ld le lc ld Interconnect: even la Self inductance Laa > 0 Spiral inductor lc Interconnect: odd Mutual inductance Lad > 0 Same current directions have a positive mutual inductance. Lab = 0 Orthogonal current directions have no mutual inductance. Lac < 0 Oppositive current directions have a negative mutual inductance. P. 12 Ke-Ying. Su Ph. D.

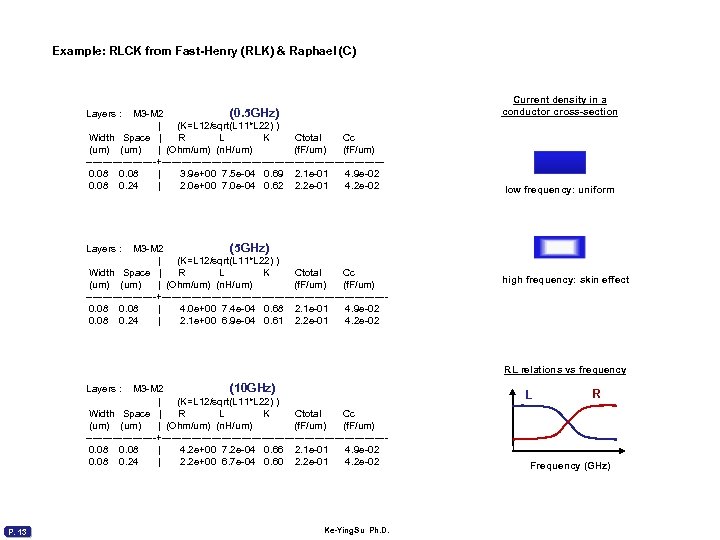Example: RLCK from Fast-Henry (RLK) & Raphael (C) M 3 -M 2 (0. 5 GHz) | (K=L 12/sqrt(L 11*L 22) ) Width Space | R L K Ctotal Cc (um) | (Ohm/um) (n. H/um) (f. F/um) -----------+---------------------------------0. 08 | 3. 9 e+00 7. 5 e-04 0. 69 2. 1 e-01 4. 9 e-02 0. 08 0. 24 | 2. 0 e+00 7. 0 e-04 0. 62 2. 2 e-01 4. 2 e-02 Layers : M 3 -M 2 (5 GHz) | (K=L 12/sqrt(L 11*L 22) ) Width Space | R L K Ctotal Cc (um) | (Ohm/um) (n. H/um) (f. F/um) -----------+----------------------------------0. 08 | 4. 0 e+00 7. 4 e-04 0. 68 2. 1 e-01 4. 9 e-02 0. 08 0. 24 | 2. 1 e+00 6. 9 e-04 0. 61 2. 2 e-01 4. 2 e-02 Current density in a conductor cross-section low frequency: uniform Layers : high frequency: skin effect RL relations vs frequency M 3 -M 2 (10 GHz) | (K=L 12/sqrt(L 11*L 22) ) Width Space | R L K Ctotal Cc (um) | (Ohm/um) (n. H/um) (f. F/um) -----------+----------------------------------0. 08 | 4. 2 e+00 7. 2 e-04 0. 66 2. 1 e-01 4. 9 e-02 0. 08 0. 24 | 2. 2 e+00 6. 7 e-04 0. 60 2. 2 e-01 4. 2 e-02 Layers : P. 13 Ke-Ying. Su Ph. D. L R Frequency (GHz)

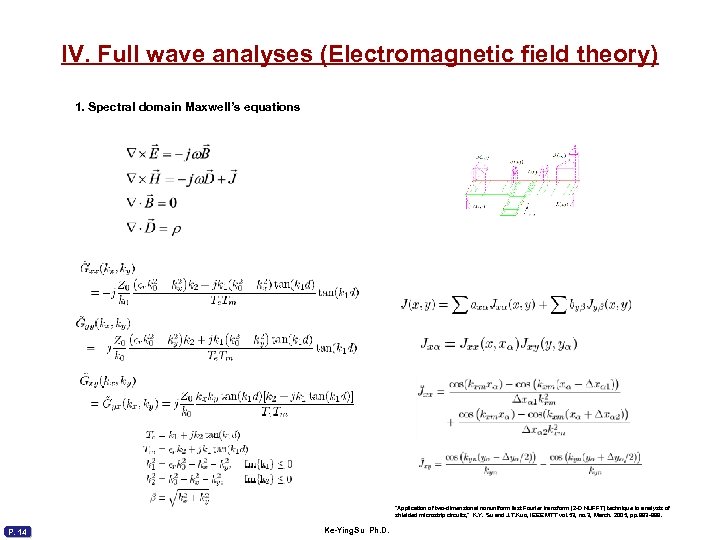IV. Full wave analyses (Electromagnetic field theory) 1. Spectral domain Maxwell’s equations “Application of two-dimensional nonuniform fast Fourier transform (2 -D NUFFT) technique to analysis of shielded microstrip circuits, ” K. Y. Su and J. T. Kuo, IEEE MTT vol. 53, no. 3, March. 2005, pp. 993 -999. P. 14 Ke-Ying. Su Ph. D.

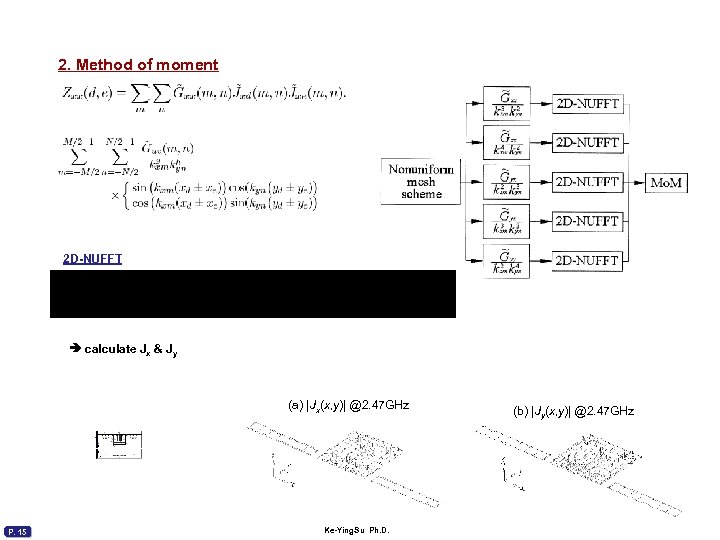2. Method of moment 2 D-NUFFT calculate Jx & Jy (a) |Jx(x, y)| @2. 47 GHz P. 15 Ke-Ying. Su Ph. D. (b) |Jy(x, y)| @2. 47 GHz

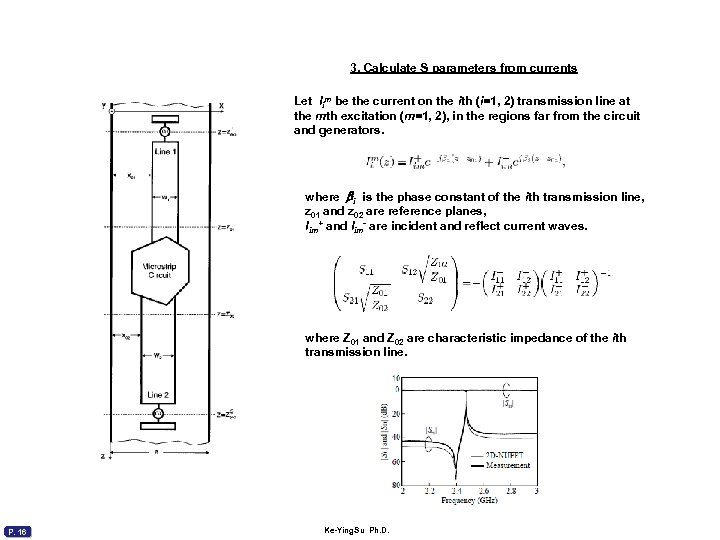3. Calculate S parameters from currents Let Iim be the current on the ith (i=1, 2) transmission line at the mth excitation (m=1, 2), in the regions far from the circuit and generators. where bi is the phase constant of the ith transmission line, z 01 and z 02 are reference planes, Iim+ and Iim- are incident and reflect current waves. where Z 01 and Z 02 are characteristic impedance of the ith transmission line. P. 16 Ke-Ying. Su Ph. D.

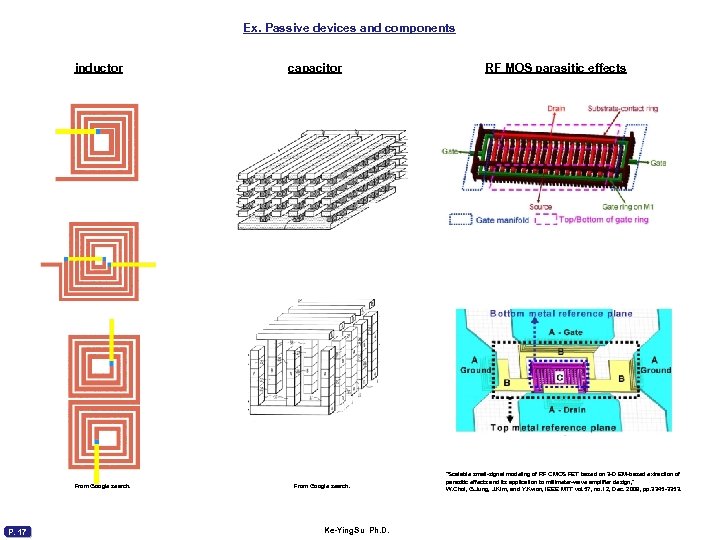Ex. Passive devices and components inductor From Google search. P. 17 capacitor From Google search. Ke-Ying. Su Ph. D. RF MOS parasitic effects “Scalable small-signal modeling of RF CMOS FET based on 3 -D EM-based extraction of parasitic effects and its application to millimeter-wave amplifier design, ” W. Choi, G. Jung, J. Kim, and Y. Kwon, IEEE MTT vol. 57, no. 12, Dec. 2009, pp. 3345 -3353.

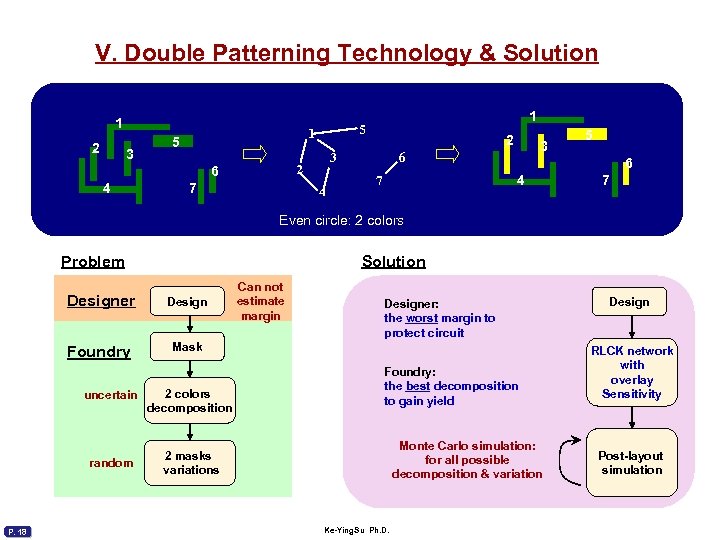V. Double Patterning Technology & Solution 1 2 3 1 5 4 7 2 3 2 6 1 5 4 3 6 7 5 6 4 7 Even circle: 2 colors Problem Solution Designer Design Foundry Mask uncertain random P. 18 Can not estimate margin 2 colors decomposition Designer: the worst margin to protect circuit Foundry: the best decomposition to gain yield Monte Carlo simulation: for all possible decomposition & variation 2 masks variations Ke-Ying. Su Ph. D. Design RLCK network with overlay Sensitivity Post-layout simulation

Backup P. 19 Ke-Ying. Su Ph. D.

Appendix It was developed to solve signal processing problems, but is applied to solve IC problems. IEEE Antenna Pro. Mag, vol. 37, no. 1, Feb. 1995, pp. 48 -56 (1) (2) (3) (4) P. 20 Ke-Ying. Su Ph. D. Determine “M” for accuracy and efficiency.

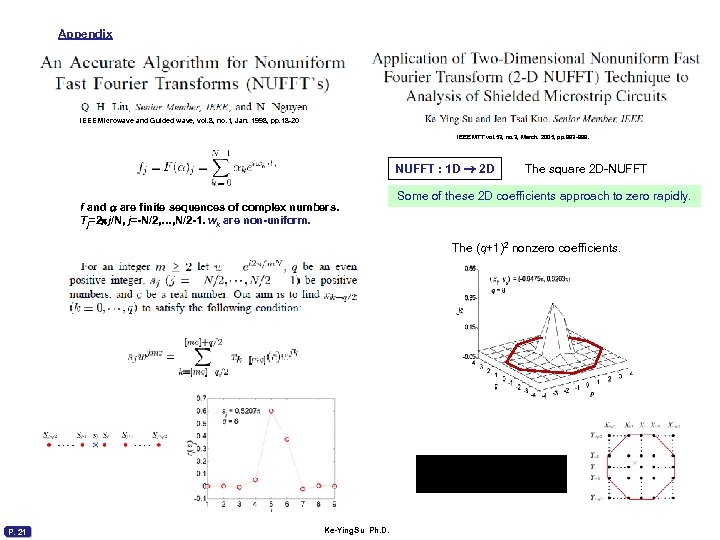Appendix IEEE Microwave and Guided wave, vol. 8, no. 1, Jan. 1998, pp. 18 -20 IEEE MTT vol. 53, no. 3, March. 2005, pp. 993 -999. NUFFT : 1 D 2 D f and a are finite sequences of complex numbers. Tj=2 pj/N, j=-N/2, …, N/2 -1. wk are non-uniform. The square 2 D-NUFFT Some of these 2 D coefficients approach to zero rapidly. The (q+1)2 nonzero coefficients. P. 21 Ke-Ying. Su Ph. D.