Напряженное и деформированное состояния Рассмотрим более детально особенности

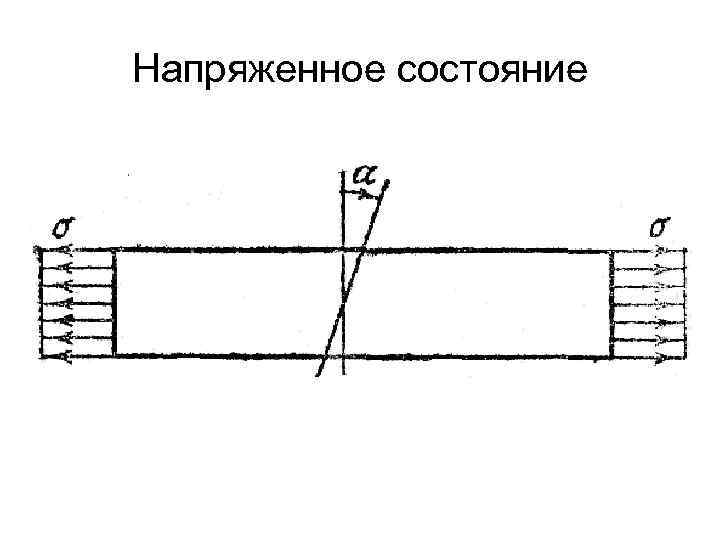
Напряженное и деформированное состояния Рассмотрим более детально особенности напряженного состояния, возникающего в однородном растянутом стержне. Определим сначала напряжения в некоторой наклонной площадке, составляющей угол α с плоскостью нормального сечения.

Напряженное состояние

Напряженное состояние Полное напряжение р на этой площадке, согласно условию однородности напряженного состояния для всех точек площадки, будет одним и тем же. Равнодействующая же внутренних сил в сечении должна быть направлена по оси стержня и равна величине растягивающей силы σF, т. е. p. Fα=σF, где Fα — площадь косого сечения

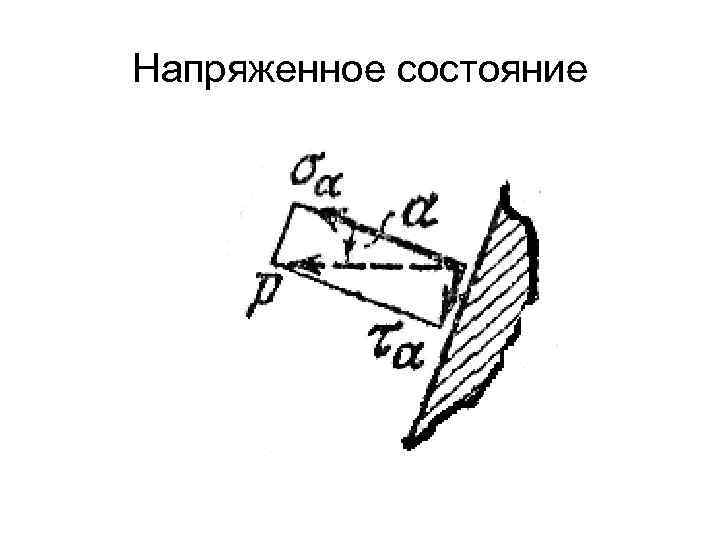
Напряженное состояние Очевидно Fα=F/cos α Таким образом, полное напряжение на наклонной площадке р=σ cos α. Раскладывая это напряжение по нормали и по касательной к наклонной площадке, находим σα=р cos α, τα=p sin α

Напряженное состояние

Напряженное состояние или с учетом σ σα=σ cos 2α τα=σ sin (2α)/2 Как видим, для одной и той же точки растянутого стержня значения возникающих в сечении напряжений оказываются различными в зависимости от ориентации секущей площадки.

Напряженное состояние Некорректно было бы утверждать, что при растяжении возникают только нормальные напряжения. Это верно только для площадок, нормальных к оси стержня. Если положить α=0, то напряжения в поперечном сечении стержня равны σα=σ τα=0

Напряженное состояние При α=90°, т. е. в продольных сечениях, σα = τα =0. Это значит, что продольные слои растянутого стержня не имеют друг с другом силового взаимодействия по боковым поверхностям. В этом смысле растяжение стержня можно уподобить растяжению пучка не связанных друг с другом параллельных нитей.

Напряженное состояние Касательное напряжение τα обращаясь в нуль в продольных и поперечных сечениях, имеет наибольшее значение на площадках, наклоненных под углом 450 к оси растянутого стержня: ταmax=σ/2

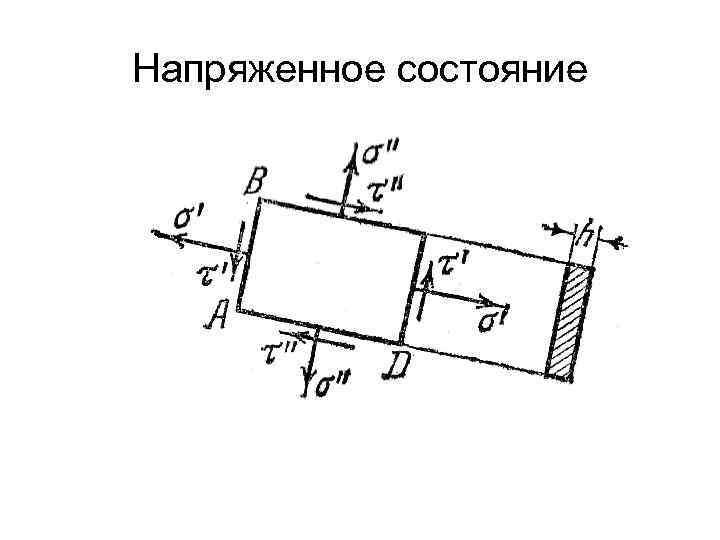
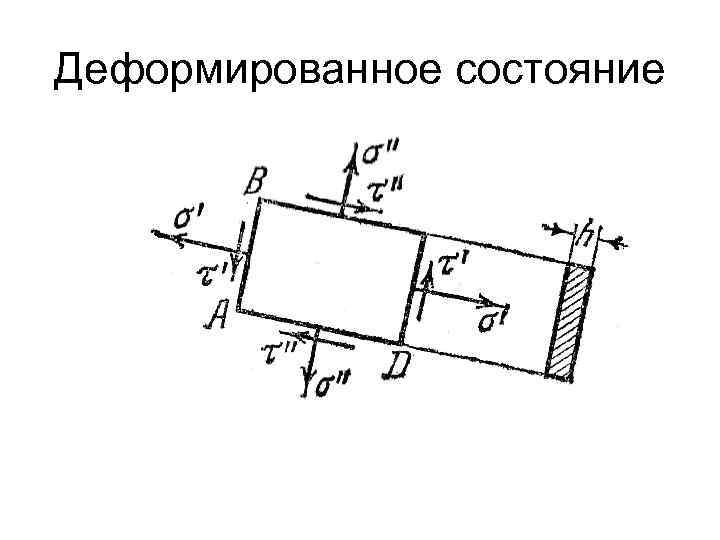
Напряженное состояние Если из растянутой полосы мы выделим прямоугольник, то на его гранях АВ и CD следует приложить напряжения σα и τα. На рисунке эти напряжения отмечены сверху штрихом. На гранях ВС и АD напряжения определяются аналогично только угол α заменяется углом α +π/2. Эти напряжения отмечены двумя штрихами

Напряженное состояние

Напряженное состояние Действительно, │σ sin (2α) /2 │ = │σ sin (2(а +π/2)) /2│ Следовательно, на двух взаимно перпендикулярных площадках (если не учитывать знаки) касательные напряжения должны быть равными.

Напряженное состояние Это условие является общей особенностью любого напряженного состояния и носит название закона парности касательных напряжений.

Напряженное состояние Этому закону можно дать наглядное толкование. Если рассмотреть произвольно взятый элемент ABCD, то легко заметить, что, независимо от величин нормальных напряжений σ' и σ", касательные напряжения τ' и τ" должны быть такой величины и иметь такое направление, чтобы моменты их пар взаимно уравновешивались.

Напряженное состояние Для произвольно взятого элемента, имеющего толщину h, очевидно, что τ' АВ h AD=τ" AD h AB. Таким образом, τ' = τ"

Напряженное состояние При этом, как видно из рисунка, векторы касательных напряжений в двух взаимно перпендикулярных площадках направлены либо оба к общему ребру (ребра А и С), либо от общего ребра (В и D).

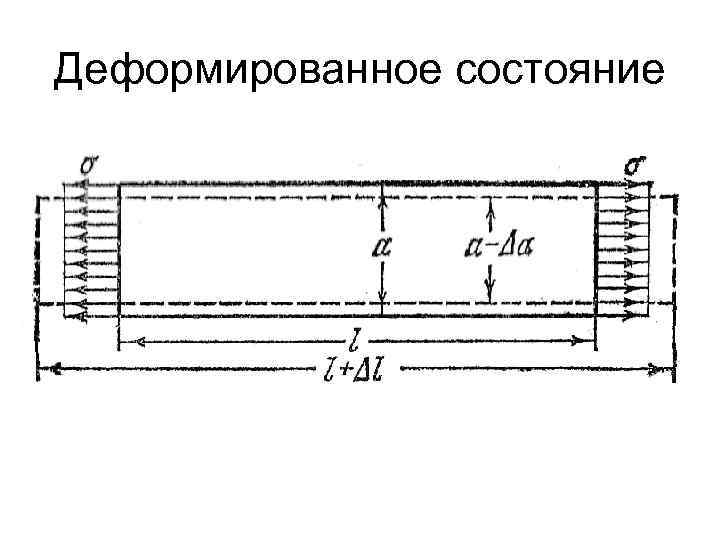
Деформированное состояние Вам известно, что удлинение стержня в осевом направлении сопровождается уменьшением его поперечных размеров Таким образом, при растяжении возникает не только продольная, но и поперечная деформация стержня

Деформированное состояние

Деформированное состояние Очевидно, что величины данных деформаций будут определяться следующим образом: εпрод=ΔL/L εпопер= Δa/a

Деформированное состояние Экспериментально установлено, что в пределах применимости закона Гука поперечная деформация пропорциональна продольной, εпопер=μ εпрод где μ —безразмерный коэффициент пропорциональности, называемый коэффициентом Пуассона.

Деформированное состояние Величина μ характеризует свойства материала и определяется экспериментально. Для всех металлов числовые значения μ лежат в пределах 0, 25 -0, 35 и вообще не может превышать 0, 5.

Деформированное состояние Рассмотрим изменение прямоугольника при растяжении. Стороны прямоугольника ABCD, начерченного на поверхности полосы, изменят свою длину, а сам прямоугольник перекосится и превратится в параллелограмм. Углы А и С уменьшатся, а В и D — увеличатся.

Деформированное состояние

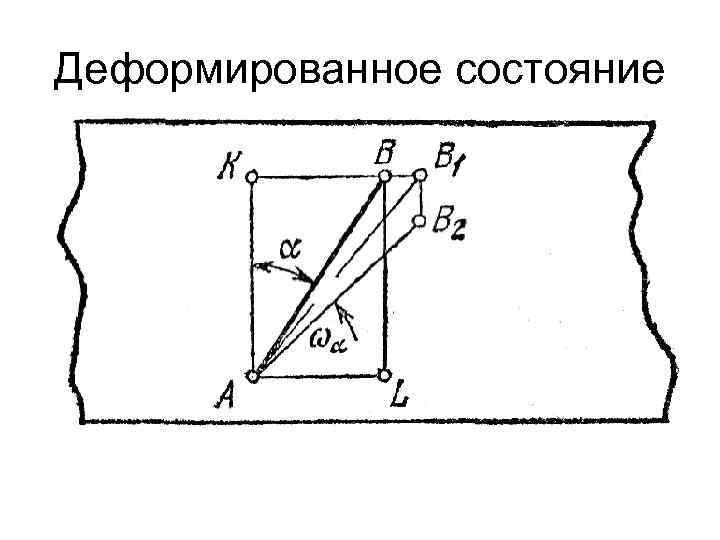
Деформированное состояние Это изменение прямого угла для заданной ориентации сторон, как нам уже известно, называется угловой деформацией или углом сдвига. Чтобы найти его, мы определим сначала углы, на которые повернутся отрезки АВ и AD. Разность этих углов и даст нам искомый угол сдвига.

Деформированное состояние Начнем с отрезка АВ. Построим на нем, как на диагонали, вспомогательный прямоугольник AKBL, стороны которого KB и AL ориентированы по продольной оси стержня.

Деформированное состояние

Вследствие продольного удлинения точка В переместится вправо и отрезок А В повернется на угол cos α ВВ 1/АВ = εпрод cos α ВК/АВ В результате поперечного сужения отрезок АВ получит дополнительный угол поворота sin α В 1 В 2/АВ = εпопер sin α АК/АВ

Деформированное состояние Сумма этих углов дает нам искомый угол поворота отрезка АВ: ω α= (εпрод + εпопер) sin α cos α или ω α= (1+ μ) sin 2 α σ /2 Е

Деформированное состояние Изменяя угол α на π/2, найдем угол поворота отрезка AD: ω (α+ π/2)= - (1+ μ) sin 2 α σ /2 Е Угловая деформация (угол сдвига) определяется разностью углов поворота отрезков, и, следовательно γ α =ω α - ω (α+ π/2) = (1+μ) sin 2α σ /Е

Деформированное состояние Сопоставляя выражение γ α с выражением τα=σ/2 sin 2α , выведенным для напряжения τα, замечаем, что угол сдвига между плоскостями А В и АС независимо от α пропорционален касательному напряжению, т. е. γ α = 2 (1+μ) τα /Е

Деформированное состояние Это соотношение в случае изотропного материала является единым для всех типов напряженных состояний и носит название закона Гука для сдвига. Опуская индекс α, напишем последнее выражение в виде γ = τ /G

Деформированное состояние где величина G называется модулем сдвига или модулем упругости второго рода: G = Е /2 (1+μ)

Деформированное состояние Модуль G измеряется в тех же единицах, что и модуль Е. Таким образом, если закон Гука для растяжения постулируется при помощи соотношений =Е ε и εпопер=μ εпрод то для сдвига он вытекает из них как следствие