Напорный пласт может отдавать воду 1 За счет

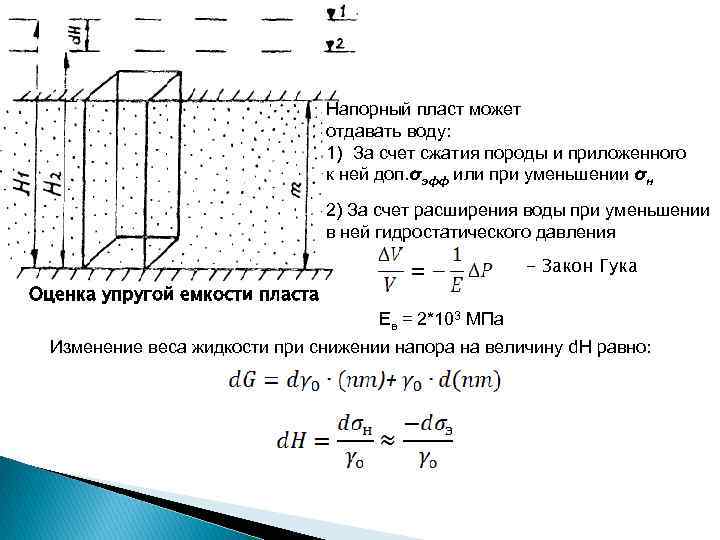Напорный пласт может отдавать воду: 1) За счет сжатия породы и приложенного к ней доп. σэфф или при уменьшении σн 2) За счет расширения воды при уменьшении в ней гидростатического давления - Закон Гука Оценка упругой емкости пласта Ев = 2*103 МПа Изменение веса жидкости при снижении напора на величину d. H равно:

Согласно закону Гука для воды: Объем породы при сжатии уменьшается за счет пор и трещин, коэфф. сжимаемости ас равен: ас = 10 -3 -10 -2 МПа-1 для песков; 0, 01 -0, 1 МПа -1 глины; 10 -3 -10 -4 МПа -1 трещиноватые породы; Изменение коэффициента пористости равно: Объединим выражения:

Выражение для относительного изменения объема воды Vo, в рассматриваемом объеме породы Vп, при Где, Упругая деформация воды Сжимаемость породы Коэффициент упругоемкости – изменение объема жидкости в единице объема породы при единичном изменении напора, [м-1] или

Значения упругоемкости η* для разных видов пород, [м-1]: 0, 5 - 5*10 -4 – пески; 10 -4 -10 -3 – супеси, суглинки; 10 -5 – 10 -6 – чисто трещиноватые породы;

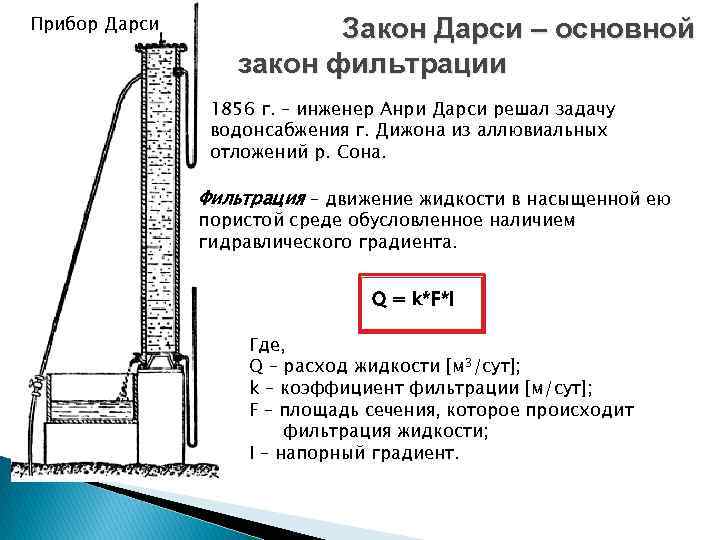Прибор Дарси Закон Дарси – основной закон фильтрации 1856 г. – инженер Анри Дарси решал задачу водонсабжения г. Дижона из аллювиальных отложений р. Сона. Фильтрация – движение жидкости в насыщенной ею пористой среде обусловленное наличием гидравлического градиента. Q = k*F*I Где, Q – расход жидкости [м 3/сут]; k – коэффициент фильтрации [м/сут]; F – площадь сечения, которое происходит фильтрация жидкости; I – напорный градиент.

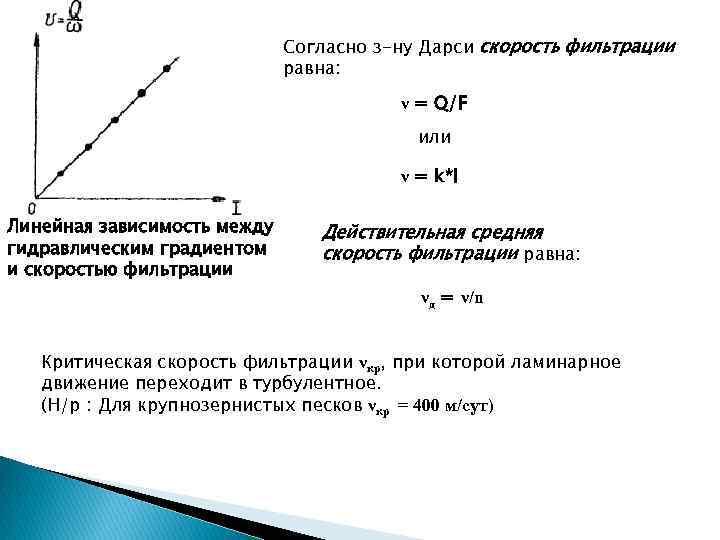Согласно з-ну Дарси скорость фильтрации равна: ν = Q/F или ν = k*I Линейная зависимость между гидравлическим градиентом и скоростью фильтрации Действительная средняя скорость фильтрации равна: νд = ν/n Критическая скорость фильтрации νкр, при которой ламинарное движение переходит в турбулентное. (Н/р : Для крупнозернистых песков νкр = 400 м/сут)

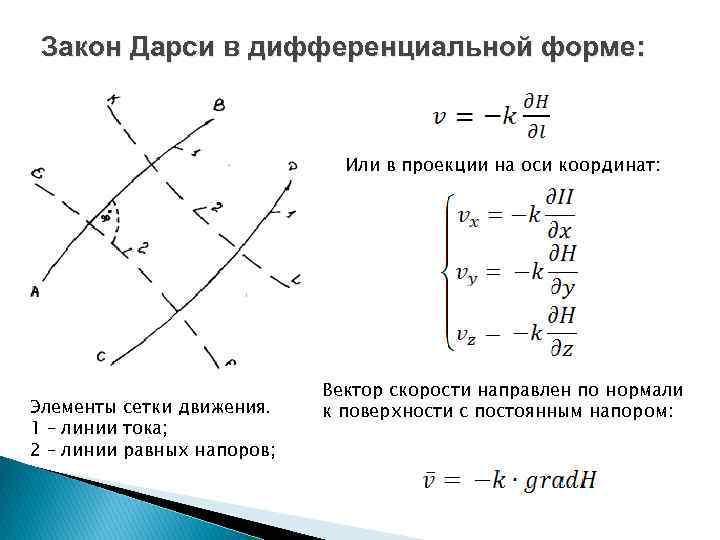Закон Дарси в дифференциальной форме: Или в проекции на оси координат: Элементы сетки движения. 1 – линии тока; 2 – линии равных напоров; Вектор скорости направлен по нормали к поверхности с постоянным напором:

Линейный закон фильтрации в трещиноватых породах. Уравнение Буссинеска: b – ширина трещины; lm - среднее расстояние между параллельными трещинами;

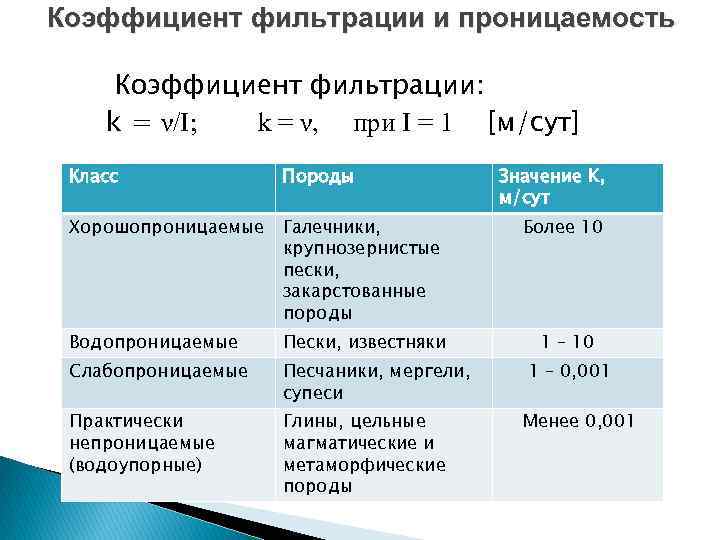Коэффициент фильтрации и проницаемость Коэффициент фильтрации: k = ν/I; k = ν, при I = 1 [м/сут] Класс Породы Значение K, м/сут Хорошопроницаемые Галечники, крупнозернистые пески, закарстованные породы Более 10 Водопроницаемые Пески, известняки 1 – 10 Слабопроницаемые Песчаники, мергели, супеси Практически непроницаемые (водоупорные) Глины, цельные магматические и метаморфические породы 1 – 0, 001 Менее 0, 001

Проницаемость параметр породы характеризующий её способность пропускать флюиды [м 2 ; 1 Д ~ 1*10 -12 м 2 ; 1 мкм 2] Кпр характеризует площадь сечения каналов пористой среды, по которым происходит фильтрация. Проницаемость: - Абсолютная; - Фазовая или эффективная; - Относительная.

Классификация пород по проницаемости К проницаемые (kпр > 10 -2 мкм 2): грубообломочные осадочные породы (галечники, гравий), сцементированные и отсортированные песчаноалеврито-глинистые породы, трещиноватые и кавернозно-трещинные известково-магнезиальные породы, трещиноватые метаморфические и магматические породы, nобщ = 20 -40%; Полупроницаемые (10 -4< kпр <10 -2 мкм 2): глинистые пески, некоторые разности алевролитов и песчаников n = 10 -15 %, карбонатные породы, микротрещиноватые известняки и доломиты. Практическии непроницаемые (kпр = 10 -4 - 10 -6 мкм 2): глины, аргиллиты, глинистые сланцы, мергели с субкапиллярными порами, сильно сцементированные песчаники и алевролиты, плотный мел, известняки, невыветрелые метаморфические и магматические породы, n глин и меловидных известняков n = до 50%, а аргиллитов, сланцев, мергелей, метаморфических и магматических пород n ≤ 6 -8%. Породы-экраны нефти и газа (kпр <10 -6 мкм 2): каменная соль, ангидрит, глины слабопесчанистые, пластичные нетрещиноватые, породы в многолетнемерзлых зонах.

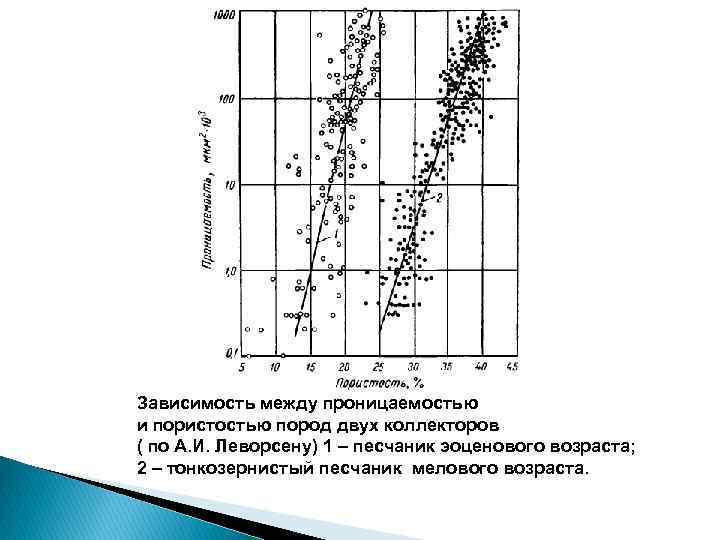Зависимость между проницаемостью и пористостью пород двух коллекторов ( по А. И. Леворсену) 1 – песчаник эоценового возраста; 2 – тонкозернистый песчаник мелового возраста.

Фазовая проницаемость пи

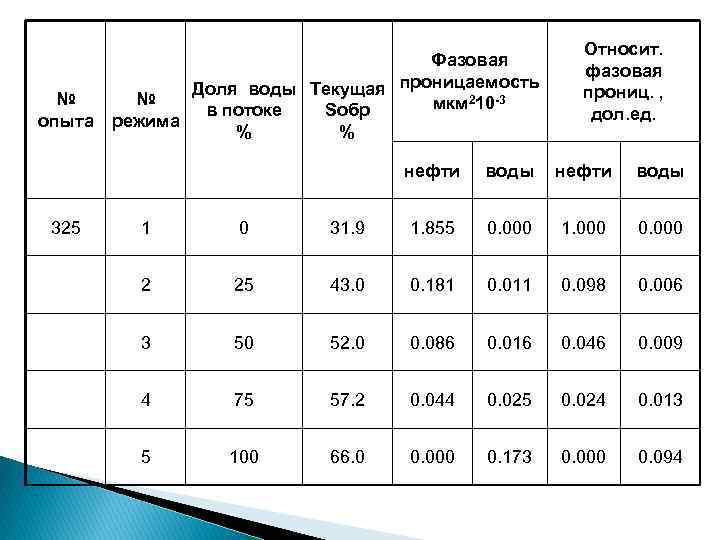Фазовая Доля воды Текущая проницаемость № № мкм 210 -3 в потоке Sобр опыта режима % % Относит. фазовая прониц. , дол. ед. нефти 325 воды нефти воды 1 0 31. 9 1. 855 0. 000 1. 000 0. 000 2 25 43. 0 0. 181 0. 011 0. 098 0. 006 3 50 52. 0 0. 086 0. 016 0. 046 0. 009 4 75 57. 2 0. 044 0. 025 0. 024 0. 013 5 100 66. 0 0. 000 0. 173 0. 000 0. 094

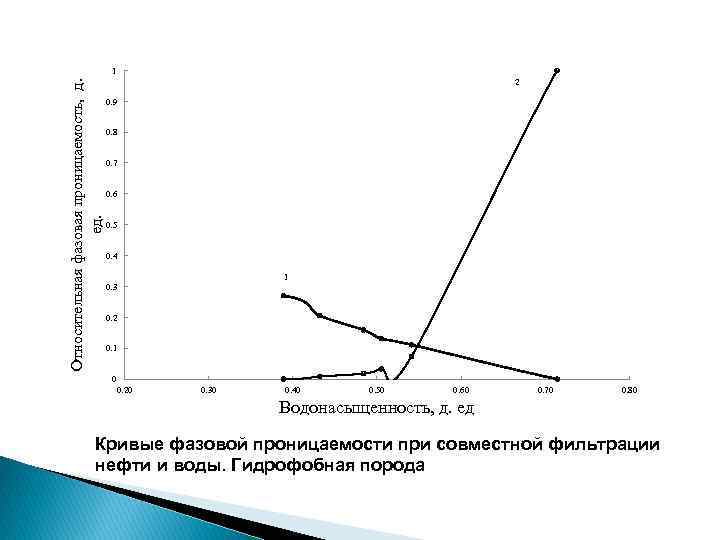Относительная фазовая проницаемость, д. ед. 1 2 0. 9 0. 8 0. 7 0. 6 0. 5 0. 4 1 0. 3 0. 2 0. 1 0 0. 20 0. 30 0. 40 0. 50 0. 60 0. 70 0. 80 Водонасыщенность, д. ед Кривые фазовой проницаемости при совместной фильтрации нефти и воды. Гидрофобная порода

Функция Стоуна – эмпирическая зависимость, описывающая многофазную фильтрацию в Гидрофобных коллекторах Krw, Krn - относительные фазовые проницаемости, Sw, n – насыщенность водой или нефтью соответственно, Swr, Snr – остаточные водо- и нефтенасыщенности.

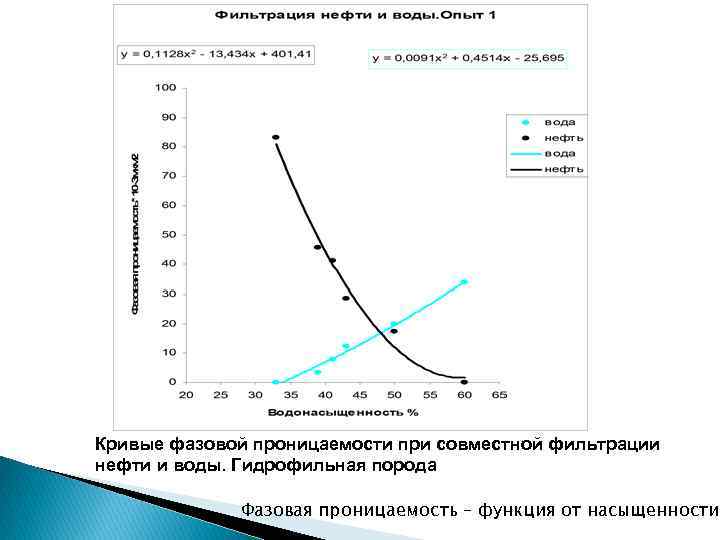Кривые фазовой проницаемости при совместной фильтрации нефти и воды. Гидрофильная порода Фазовая проницаемость – функция от насыщенности

Зависимость Кори –ван- Генухтена- Мулема

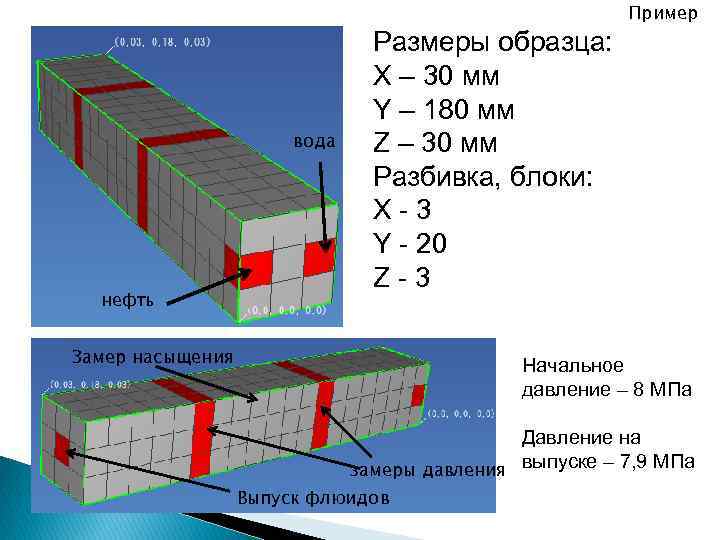вода нефть Размеры образца: X – 30 мм Y – 180 мм Z – 30 мм Разбивка, блоки: X-3 Y - 20 Z-3 Замер насыщения Пример Начальное давление – 8 МПа Давление на замеры давления выпуске – 7, 9 МПа Выпуск флюидов

Пример. В полностью водонасыщенный пласт закачивается нефть до воды.

Факторы влияющие на параметры проницаемости: Изменение напряженного состояния горных пород В глинистых породах – увеличение температуры; Изменение минерализации и химического состава воды;

Границы применения закона Дарси Верхние границы – проявление инерционных при высоких скоростях фильтрации; Нижние границы – неньютоновские реологические свойства жидкости и ее взаимодействие со скелетом породы при малых скоростях фильтрации.

Верхние границы применения закона Дарси Число Рейнольдса для пористых пород: Число Рейнольдса для трещиноватых пород: Для трещин больших размеров: I = av+bv 2

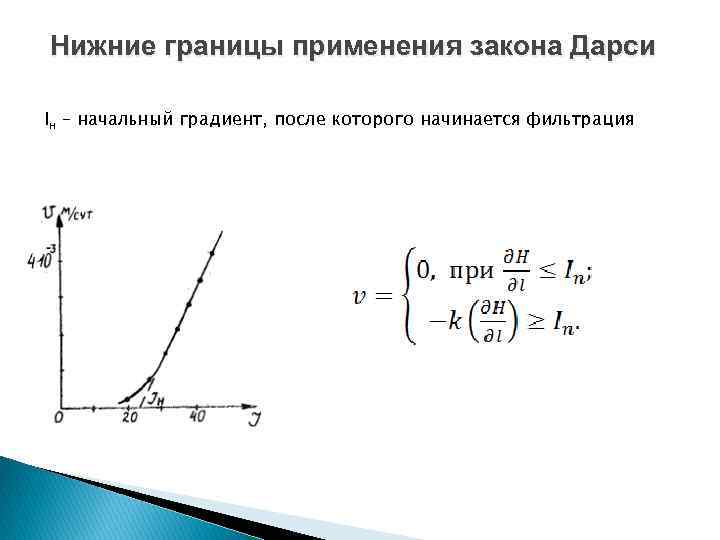Нижние границы применения закона Дарси Iн – начальный градиент, после которого начинается фильтрация