Найти координаты векторов 3 a b -2 0

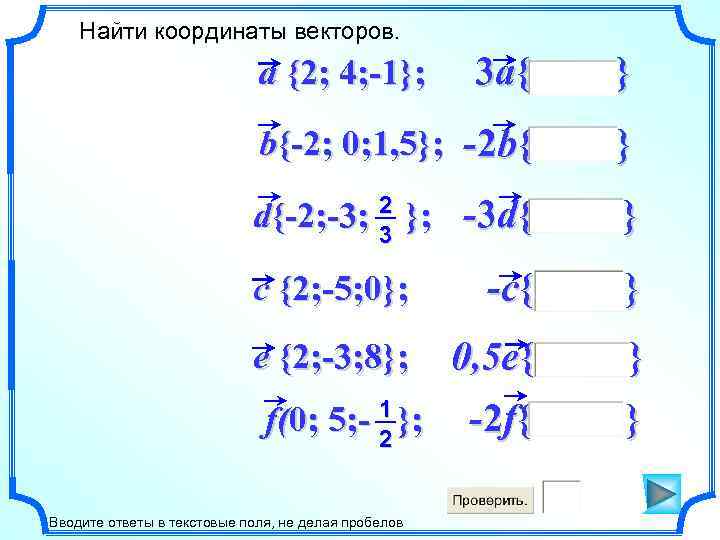
Найти координаты векторов. 3 a{ } b{-2; 0; 1, 5}; -2 b{ } d{-2; -3; 2 }; -3 d{ 3 } c {2; -5; 0}; -c { } e {2; -3; 8}; 0, 5 e{ } -2 f{ } a {2; 4; -1}; f(0; 5; - 1 }; 2 Вводите ответы в текстовые поля, не делая пробелов

Найти координаты векторов. a {2; 4; 3}; c {3; 2; -3}; a +c { } b{-2; 0; 4}; d{-2; -3; -1}; b+d{ } c {2; -5; 4}; e {2; -3; -9}; c +e{ } f(0; 5; -3}; d{-2; -3; 7}; f - d{ } b{-2; 0; -1}; d{-2; -3; -4}; b - d{ } a {2; 4; 0}; c {3; 2; -9}; a - c{ } Вводите ответы в текстовые поля, не делая пробелов

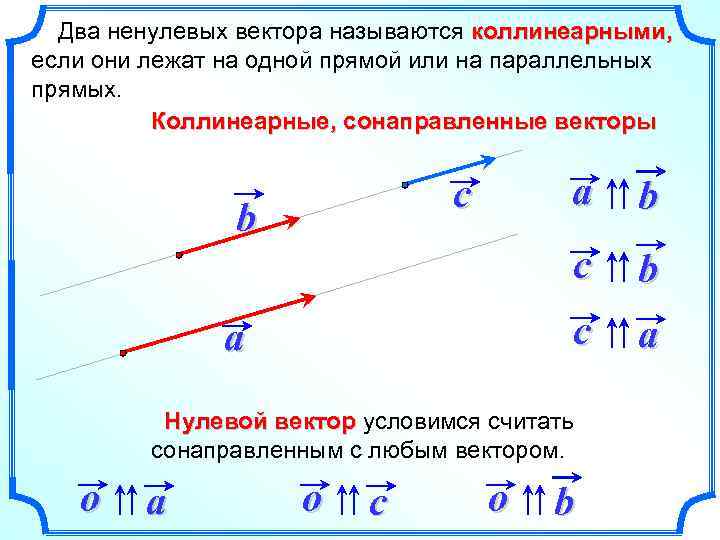
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные, сонаправленные векторы a a b c b b c c a Нулевой вектор условимся считать сонаправленным с любым вектором. o a o c o b

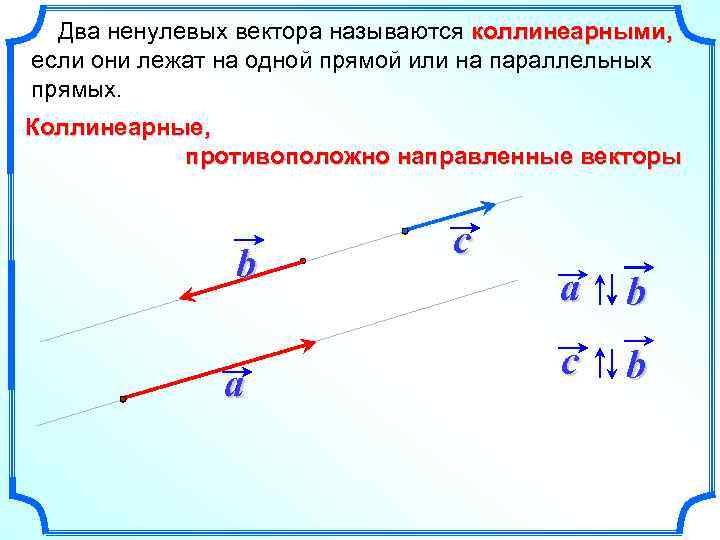
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные, противоположно направленные векторы b a c a b c b

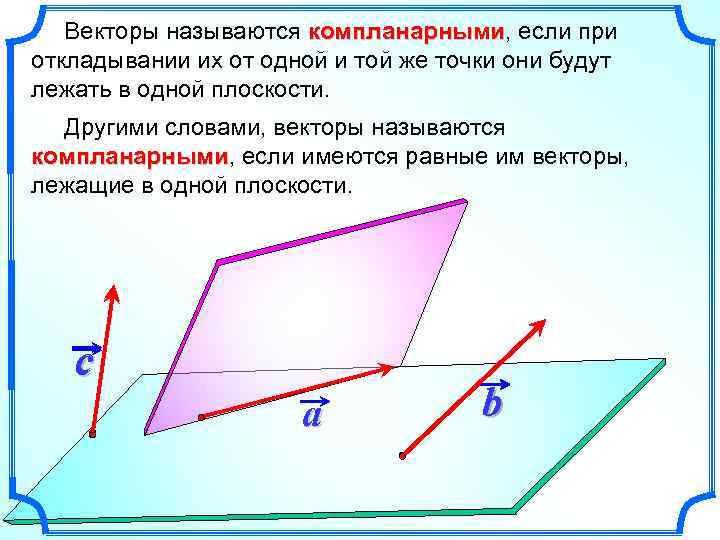
Векторы называются компланарными, если при компланарными откладывании их от одной и той же точки они будут лежать в одной плоскости. Другими словами, векторы называются компланарными, если имеются равные им векторы, компланарными лежащие в одной плоскости. c a b

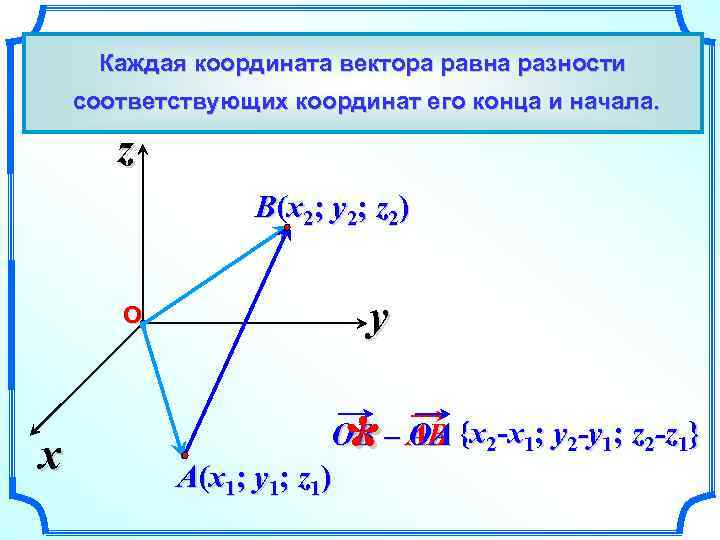
Выразим координаты вектора АВ равна разности Каждая координата вектора через координаты его начала А и конца В. соответствующих координат его конца и начала. Из АОB, AB = AО + ОB = –ОA + ОB z B(x 2; y 2; z 2) О x y * OB – AB {x 2 -x 1; y 2 -y 1; z 2 -z 1} OA A(x 1; y 1; z 1)

A(3; 5; 7) – B(5; 4; -1) A (3; 5; 7), B (5; 4; -1), AB AB{2; -1; -8} N (3; 2; -3), O (0; 0; 0), ON Радиус-вектор ON{3; 2; -3} P (2; -1; 0), C (4; -4; 2), PC R(-4; 0; -4), T (0; 5; -1), TR D(-3; -4; 0), O (0; 0; 0), OD Радиус-вектор OD{-3; -4; 0} P(2; -1; 0) – C(4; -4; 2) PC{2; -3; 2} R(-4; 0; -4) – T(0; 5; -1) TR{-4; -5; -3}

Найдите координаты векторов R(2; 7; 1); M(-2; 7; 3); RM P(-5; 1; 4); D(-5; 7; -2); PD R(-3; 0; -2); N(0; 5; -3); RN A(0; 3; 4); B(-4; 0; -3); BA A(-2; 7; 5); B(-2; 0; -3); AB R(-7; 7; -6); T(-2; -7; 0); RT M(-2; 7; 3) – R(2; 7; 1) RM{-4; 0; 2} N(0; 5; -3) – R(-3; 0; -2) RN{3; 5; -1} D(-5; 7; -2) – P(-5; 1; 4) PD{ 0; 6; -6} A(0; 3; 4) – B(-4; 0; -3) BA{4; 3; 7} B(-2; 0; -3) T(-2; -7; 0) – A(-2; 7; 5) – R(-7; 7; -6) AB{0; -7; -8} RT{5; -14; 6}

Найти координаты векторов. R(2; 7; 1); M(-2; 7; 3); RM { } P(-5; 1; 4); D(-5; 7; -2); PD { } R(-3; 0; -2); N(0; 5; -3); RN { } A(0; 3; 4); B(-4; 0; -3); BA { } A(-2; 7; 5); B(-2; 0; -3); AB { } R(-7; 7; -6); T(-2; -7; 0); RT { } Вводите ответы в текстовые поля, не делая пробелов

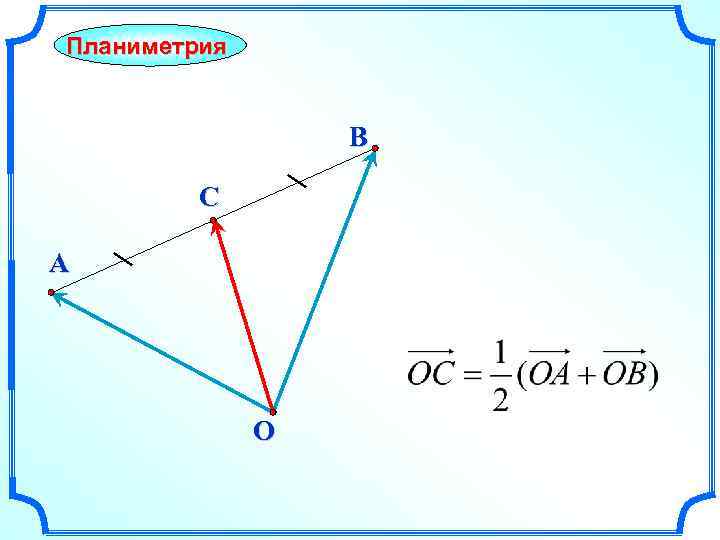
Планиметрия B C A O

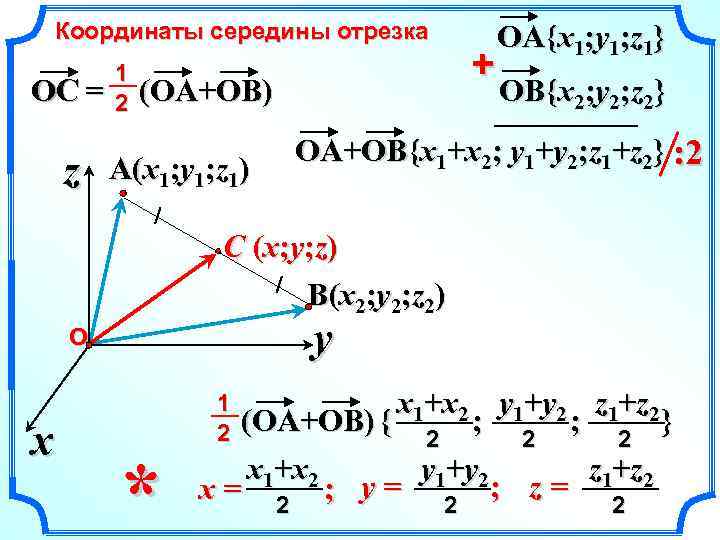
Координаты середины отрезка OC = z 1 2 (OA+OB) A(x 1; y 1; z 1) + OA{x 1; y 1; z 1} OB{x 2; y 2; z 2} OA+OB{x 1+x 2; y 1+y 2; z 1+z 2} : 2 C (x; y; z) B(x 2; y 2; z 2) y О x * x 1+x 2 y 1+y 2 z 1+z 2 (OA+OB) { ; ; } 2 2 2 y 1+y 2 z 1+z 2 x 1+x 2 x= 2 ; y= 2 ; z= 2 1 2

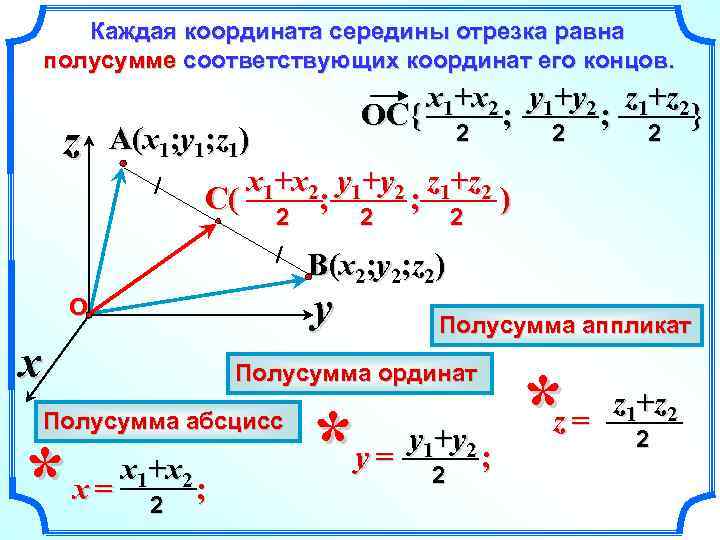
Каждая координата середины отрезка равна полусумме соответствующих координат его концов. z x 1+x 2 y 1+y 2 z 1+z 2 ; ; } OC{ 2 2 A(x 1; y 1; z 1) x 1+x 2 y 1+y 2 z 1+z 2 C( ; ; ) 2 2 2 2 B(x 2; y 2; z 2) y О x Полусумма аппликат Полусумма ординат Полусумма абсцисс * x= x 1+x 2 2 ; * y= y 1+y 2 2 ; * z= z 1+z 2 2

№ 424 (a) Найдите координаты середины отрезка A(0; 3; -4), B(-2; 2; 0), середина – точка M(-1; 2, 5; -2 ) Полусумма абсцисс x= Полусумма ординат y= Полусумма аппликат z= x 1+x 2 2 ; x= 0+(-2) 2 = -1 y 1+y 2 ; y= z 1+z 2 ; -4 +0 z = 2 = -2 2 2 3 +2 2 = 2, 5

Найдите координаты середины отрезков R(2; 7; 4); M(-2; 7; 2); C ( 2+(-2) ; 7 + 7 ; 4 + 2 ) 2 2 2 ( -5+(-5) ; 1 + 7 ; 3 +(-9)) P(-5; 1; 3); D(-5; 7; -9); C 2 2 2 -3+0 0+5 -3+(-5) ; ; ); R(-3; 0; -3); N(0; 5; -5); C ( 2 2 2 A(0; -6; 9); B(-4; 2; -6); C(0; 7; 3) C(-5; 4; -3) C(-1, 5; 2, 5; -4) ( 0+(-4) ; -6+2 ; 9+(-6)); C 2 2 7+(-2) A(7; 7; 0); B(-2; 0; -4); C ( 2 R(-7; 4; 0); T(-2; -7; 0); C ( 2 2 C(-2; 1, 5) 7 + 0 0+(-4) C(2, 5; 3, 5; -2) ; ; ); 2 2 -7+(-2) 4+(-7) 0+0 ; ; ); C(-4, 5; -1, 5; 0) 2 2 2

Найти координаты середин отрезков. R(2; 7; 4); M(-2; 7; 2); C( ) P(-5; 1; 3); D(-5; 7; -9); C ( ) R(-3; 0; -3); N(0; 5; -5); C ( ) A(0; -6; 9); B(-4; 2; -6); C( ) A(7; 7; 0); B(-2; 0; -4); C ( ) R(-7; 4; 0); T(-2; -7; 0); C( ) Вводите ответы в текстовые поля, не делая пробелов.

Обратная задача. x 1 y 1 z 1 A(5; 4; -6) x y z A(5; 4; -6); C(-3; 2; 10) x 2 y 2 z 2 C(-3; 2; 10) – середина отрезка AB B(a; b; c) Найти: B(a; b; c) z 1+z 2 y 1+y 2 x 1+x 2 z= y= ; x= 2 ; 2 2 Дано: 5+a -3= 2 ; – 6=5+a a = – 11 2 4+b 2= 2 ; 4=4+b b=0 2 -6 + c 10 = 2 20 = -6 + c c = 26 B(-11; 0; 26) 2

Вычисление длины вектора по его координатам z a {x; y; z} По правилу параллелепипеда OA OA 1 2 2 OA + OA 3 OA 2=2= OA 1+ +OA 2222 + OA 322 A 3 OA 1 = xi = x A zk a xi О OA 2 = y j = y yj A 2 A 1 x y 2 OA 3 = zk = z 2 2 a = x + y + z * a = x +y + z 2 2

z Расстояние между двумя точками M 2(x 2; y 2; z 2) – y О x M 1(x 1; y 1; z 1) M 2(x 2; y 2; z 2) M 1(x 1; y 1; z 1) M 1 M 2 {x 2–x 1; y 2–y 1; z 2–z 1} * 2 a = x +y + z M 1 M 2 = (x 2–x 1)2+(y 2–y 1)2+(z 2–z 1)2 d= d (x 2–x 1)2+(y 2–y 1)2+(z 2–z 1)2 2

№ 426 (a) Найдите длину вектора АВ A(-1; 0; 2) 1 способ 1) – и B(1; -2; 3) a = x 2 + y 2 + z 2 B(1; -2; 3) A(-1; 0; 2) 2) AB = 22+(-2)2+12 = 9 = 3 AB{2; -2; 1} 2 способ AB = (x 2–x 1)2+(y 2–y 1)2+(z 2–z 1)2 AB = (1+1)2+(– 2– 0)2+(3– 2)2

№ 426 (б) Найдите длину вектора АВ A(-35; -17; 20) B(-34; -5; 8) a = x 2 + y 2 + z 2 1 способ 1) и B(-34; -5; 8) 2) 1 способ AB = 12+122+(-12)2 = – A(-35; -17; 20) = 289 = 17 AB{ 1; 12; -12} 2 способ AB = (x 2–x 1)2+(y 2–y 1)2+(z 2–z 1)2 2 способ AB = (-34+35)2+(– 5+17)2+(8– 20)2