НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ. ВЗАИМНО ПРОСТЫЕ ЧИСЛА.
Какое наибольшее число композиций можно составить из 96 васильков и 72 ромашек, если надо использовать все цветы? 72 96 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96. 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72. 24 - Наибольший Общий Делитель чисел 72 и 96. 72 : 24 = 3 96 : 24 = 4
Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей. Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел m или n не ноль.
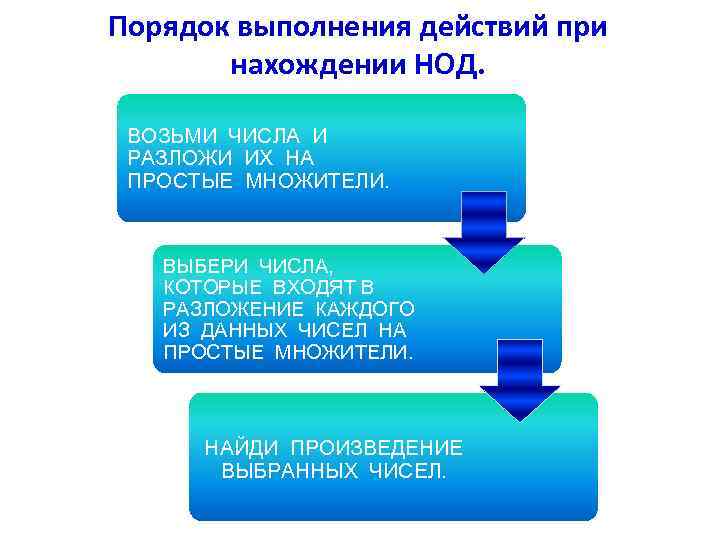
Порядок выполнения действий при нахождении НОД. ВОЗЬМИ ЧИСЛА И РАЗЛОЖИ ИХ НА ПРОСТЫЕ МНОЖИТЕЛИ. ВЫБЕРИ ЧИСЛА, КОТОРЫЕ ВХОДЯТ В РАЗЛОЖЕНИЕ КАЖДОГО ИЗ ДАННЫХ ЧИСЕЛ НА ПРОСТЫЕ МНОЖИТЕЛИ. НАЙДИ ПРОИЗВЕДЕНИЕ ВЫБРАННЫХ ЧИСЕЛ.
Шаг Володи 75 см, а шаг Кати 60 см. На каком наименьшем расстоянии они оба сделают по целому числу шагов? Числа кратные 75 : Числа кратные 60 : Володя 75, 150, 225, 300, 375, 450, 525, 600, 675, 750. 60, 120, 180, 240, 300, 360, 420, 480, 540, 600, 660. Катя 300 – Наименьшее Общее Кратное чисел 75 и 60. 300 : 75 = 4 300 : 60 = 5
Наиме ньшее о бщее кра тное (НОК) двух целых чисел m и n есть наименьшее натуральное число, которое делится на m и n без остатка. Наименьшее общее кратное для нескольких чисел — это наименьшее натуральное число, которое делится на каждое из этих чисел. Одно из наиболее частых применений НОК — приведение дробей к общему знаменателю.
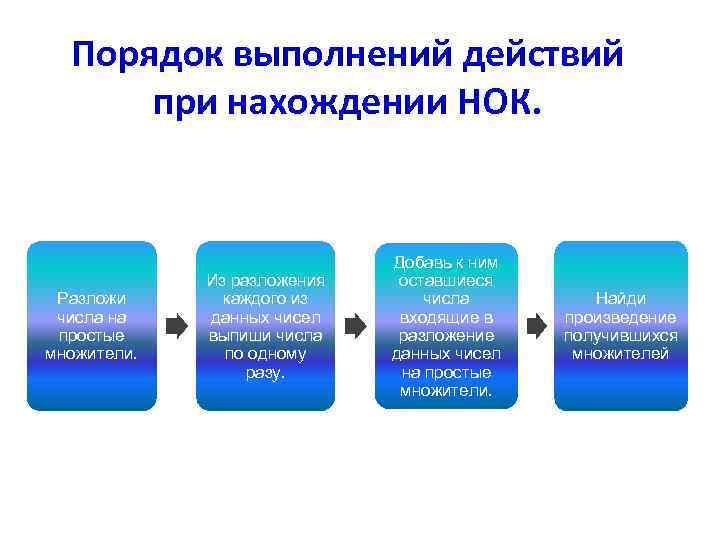
Порядок выполнений действий при нахождении НОК. Разложи числа на простые множители. Из разложения каждого из данных чисел выпиши числа по одному разу. Добавь к ним оставшиеся числа входящие в разложение данных чисел на простые множители. Найди произведение получившихся множителей
Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме 1. Примеры: 14 и 25 взаимно просты, а 15 и 25 не взаимно просты (у них имеется общий делитель 5). Если в наборе чисел любые два взаимно просты, то такие числа называются попарно взаимно простыми. Для двух чисел понятия «взаимно простые» и «попарно взаимно простые» совпадают. Примеры 8, 15 — не простые, но взаимно простые. 6, 8, 9 — взаимно простые числа, но не попарно взаимно простые. 8, 15, 49 — попарно взаимно простые.
Спасибо за внимание!
Скачать презентацию НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ ВЗАИМНО ПРОСТЫЕ
15 октября.ppt