Надёжность.ppt
- Количество слайдов: 50

НАДЁЖНОСТЬ СТРОИТЕЛЬНЫХ ОБЪЕКТОВ
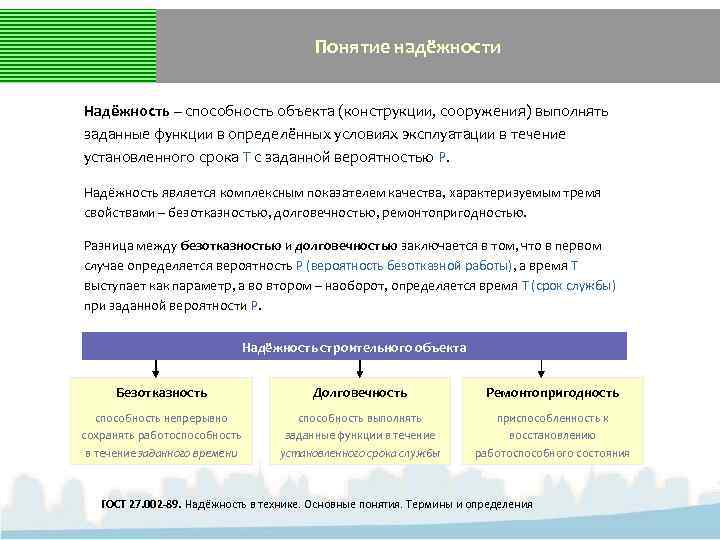
Понятие надёжности Надёжность – способность объекта (конструкции, сооружения) выполнять заданные функции в определённых условиях эксплуатации в течение установленного срока Т с заданной вероятностью Р. Надёжность является комплексным показателем качества, характеризуемым тремя свойствами – безотказностью, долговечностью, ремонтопригодностью. Разница между безотказностью и долговечностью заключается в том, что в первом случае определяется вероятность Р (вероятность безотказной работы), а время Т выступает как параметр, а во втором – наоборот, определяется время Т (срок службы) при заданной вероятности Р. Надёжность строительного объекта Безотказность Долговечность Ремонтопригодность способность непрерывно сохранять работоспособность в течение заданного времени способность выполнять заданные функции в течение установленного срока службы приспособленность к восстановлению работоспособного состояния ГОСТ 27. 002 -89. Надёжность в технике. Основные понятия. Термины и определения
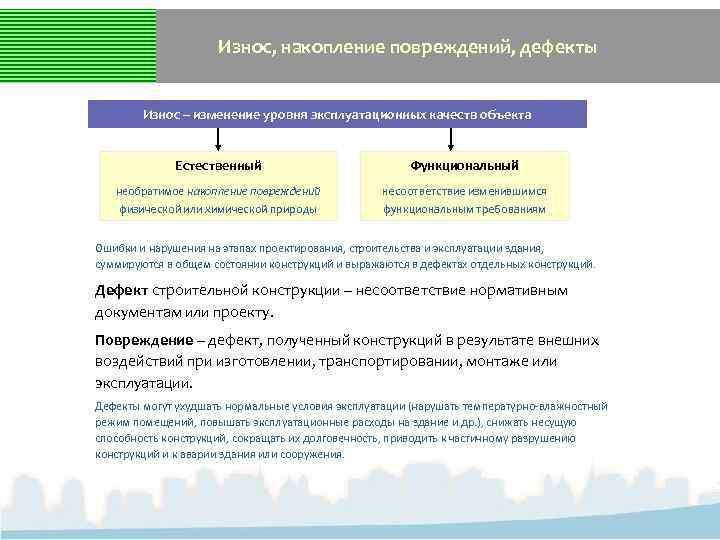
Износ, накопление повреждений, дефекты Износ – изменение уровня эксплуатационных качеств объекта Естественный Функциональный необратимое накопление повреждений физической или химической природы несоответствие изменившимся функциональным требованиям Ошибки и нарушения на этапах проектирования, строительства и эксплуатации здания, суммируются в общем состоянии конструкций и выражаются в дефектах отдельных конструкций. Дефект строительной конструкции – несоответствие нормативным документам или проекту. Повреждение – дефект, полученный конструкций в результате внешних воздействий при изготовлении, транспортировании, монтаже или эксплуатации. Дефекты могут ухудшать нормальные условия эксплуатации (нарушать температурно-влажностный режим помещений, повышать эксплуатационные расходы на здание и др. ), снижать несущую способность конструкций, сокращать их долговечность, приводить к частичному разрушению конструкций и к аварии здания или сооружения.
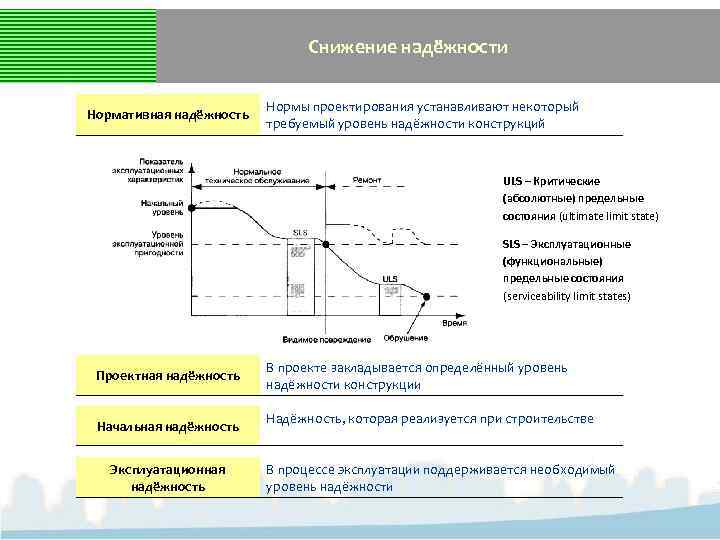
Снижение надёжности Нормативная надёжность Нормы проектирования устанавливают некоторый требуемый уровень надёжности конструкций ULS – Критические (абсолютные) предельные состояния (ultimate limit state) SLS – Эксплуатационные (функциональные) предельные состояния (serviceability limit states) Проектная надёжность Начальная надёжность Эксплуатационная надёжность В проекте закладывается определённый уровень надёжности конструкции Надёжность, которая реализуется при строительстве В процессе эксплуатации поддерживается необходимый уровень надёжности

Повреждение и отказ в терминах теории надёжности Повреждение – событие, заключающееся в нарушении исправного состояния объекта при сохранении работоспособного состояния. Работоспособный объект в отличие от исправного должен удовлетворять лишь тем требованиям, выполнение которых обеспечивает нормальное применение объекта по назначению. Отказ – событие, заключающееся в нарушении работоспособного состояния объекта. Классификация отказов Признак классификации Вид отказа Примеры отказов По характеру проявления отказов внезапный хрупкое разрушение постепенный пластическое разрушение По связи с другими отказами независимый обрушение плит покрытия из-за перегрузки зависимый обрушение плит покрытия из-за отказа фермы По возможности использования после отказа полный обрушение покрытия здания частичный обрушение плиты покрытия здания По наличию внешних признаков явный потеря устойчивости скрытый падение предварительных напряжений в арматуре
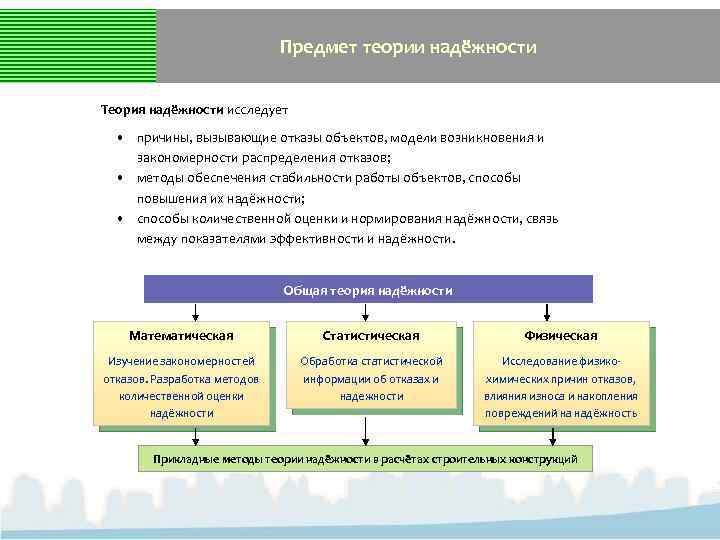
Предмет теории надёжности Теория надёжности исследует • причины, вызывающие отказы объектов, модели возникновения и закономерности распределения отказов; • методы обеспечения стабильности работы объектов, способы повышения их надёжности; • способы количественной оценки и нормирования надёжности, связь между показателями эффективности и надёжности. Общая теория надёжности Математическая Статистическая Физическая Изучение закономерностей отказов. Разработка методов количественной оценки надёжности Обработка статистической информации об отказах и надежности Исследование физикохимических причин отказов, влияния износа и накопления повреждений на надёжность Прикладные методы теории надёжности в расчётах строительных конструкций

Применение методов теории надёжности в строительстве Задачи теории надёжности в расчётах строительных конструкций: • исследование вероятностной природы запасов прочности конструкций; • разработка критериев и методов расчётной оценки безопасной работы строительных конструкций; • исследование вероятностных характеристик действующих нагрузок; • исследование вероятностных характеристик применяемых конструкционных материалов; • контроль качества при изготовлении конструкций и возведении сооружений; • оптимизация нормативных сроков службы объектов; • оценка остаточного ресурса долговечности. Причины применения методов теории надёжности в строительстве Где компромисс между экономичностью и безопасностью? С уменьшением материалоёмкости надёжность конструкций снижается Строить на века или нет? Моральное старение здания происходит зачастую значительно быстрее, чем физическое Основная область практического применения методов теории надёжности в строительстве – нормирование правил расчёта при проектировании и контроля качества при изготовлении конструкций
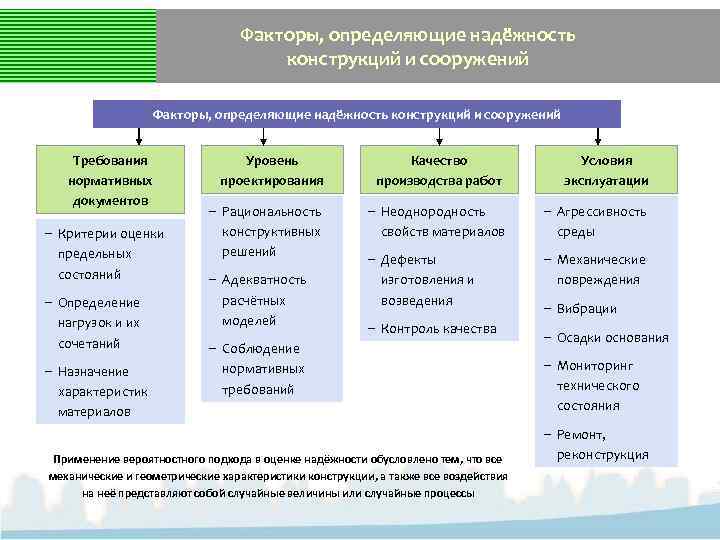
Факторы, определяющие надёжность конструкций и сооружений Требования нормативных документов ‒ Критерии оценки предельных состояний ‒ Определение нагрузок и их сочетаний ‒ Назначение характеристик материалов Уровень проектирования Качество производства работ Условия эксплуатации ‒ Рациональность конструктивных решений ‒ Неоднородность свойств материалов ‒ Агрессивность среды ‒ Дефекты изготовления и возведения ‒ Механические повреждения ‒ Адекватность расчётных моделей ‒ Контроль качества ‒ Соблюдение нормативных требований Применение вероятностного подхода в оценке надёжности обусловлено тем, что все механические и геометрические характеристики конструкции, а также все воздействия на неё представляют собой случайные величины или случайные процессы ‒ Вибрации ‒ Осадки основания ‒ Мониторинг технического состояния ‒ Ремонт, реконструкция
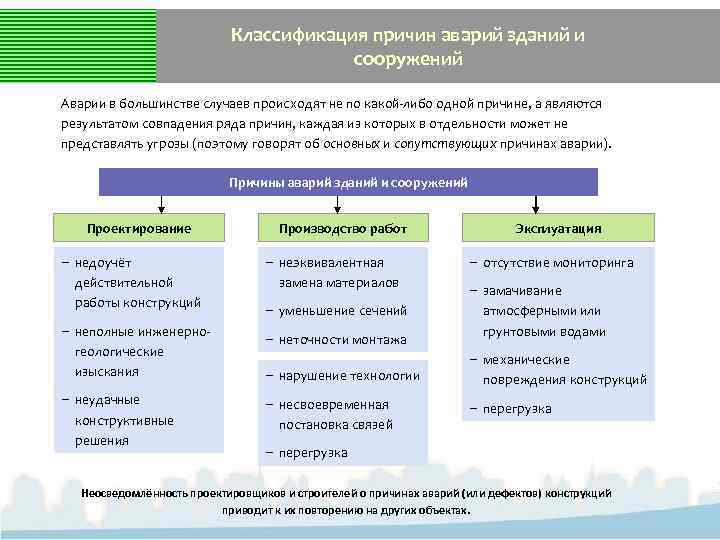
Классификация причин аварий зданий и сооружений Аварии в большинстве случаев происходят не по какой-либо одной причине, а являются результатом совпадения ряда причин, каждая из которых в отдельности может не представлять угрозы (поэтому говорят об основных и сопутствующих причинах аварии). Причины аварий зданий и сооружений Проектирование ‒ недоучёт действительной работы конструкций ‒ неполные инженерногеологические изыскания ‒ неудачные конструктивные решения Производство работ ‒ неэквивалентная замена материалов ‒ уменьшение сечений ‒ неточности монтажа Эксплуатация ‒ отсутствие мониторинга ‒ замачивание атмосферными или грунтовыми водами ‒ нарушение технологии ‒ механические повреждения конструкций ‒ несвоевременная постановка связей ‒ перегрузка Неосведомлённость проектировщиков и строителей о причинах аварий (или дефектов) конструкций приводит к их повторению на других объектах.

Классификация дефектов (аварий) зданий и сооружений По субъективным причинам: – экономия, невежество, небрежность (Мак Кейг, 1967); – ошибки и нарушения при проектировании, строительстве, эксплуатации. По объективным причинам: – несоответствующее качество материалов; эксплуатационные воздействия; стихийные бедствия; недостатки нормативных документов. По видам и материалам конструкций: – дефекты (аварии) фундаментов, колонн, стен, плит, ферм и т. д. – дефекты (аварии) каменных, железобетонных, стальных конструкций и т. д.

Факторы технического риска

1 – Ошибки проектировании • Неудачно выбранная (несоответствующая действительным условиям работы) расчётная схема (расчётная модель) конструкции или сооружения; • Проектирование фундаментов при отсутствии данных о грунтово-геологических условиях; малая глубина заложения фундаментов; недоучёт влияния новых фундаментов пристраеваемых зданий на существующие; • Неудачная привязка типового проекта здания, не предназначенного для эксплуатации в данном климатическом районе (несоответствие величины снеговой нагрузки; применение марок стали, склонных к хрупкому разрушению при пониженной температуре). • Занижение или игнорирование нагрузок, действующих на конструкции; • Ошибки при назначении марок стали, классов бетона и арматуры; • Ошибки в расчётах конструкций (при вводе исходных данных, выполнении вычислений и анализе результатов); • Неправильное размещение связей каркаса; • Неграмотные или нетехнологичные решения конструкций, узлов и соединений; • Отсутствие указаний по защите конструкций от коррозии;

2 – Ошибки при изготовлении или возведении • Применение некачественных материалов; • Уменьшение размеров сечений (диаметра арматуры, номера прокатного профиля); • Неэквивалентная замена марок стали, классов арматуры и бетона, сортов древесины; • Неправильная геодезическая разбивка осей, смещение осей от геометрических центров узлов, несоблюдение вертикальности (стен, колонн); • Несвоевременная постановка связей; • Несоблюдение технологии бетонных работ, толщины защитного слоя бетона, расстояния между стержнями; • Некачественное выполнение соединений (сварных, болтовых, клеевых); • Перегрузка конструкций при увеличении толщины или объёмного веса стяжек, засыпок; • В каменных конструкциях – отсутствие гидроизоляции, отсутствие железобетонных подушек для распределения нагрузки в местах опирания несущих конструкций на кирпичную кладку, пропуск деформационных швов, отсутствие перевязки и армирования кладки; • Недостаточная антикоррозийная защита (бетона, металлических элементов, стыков, закладных деталей); • Строительство без проекта; нарушение правил производства работ при ремонте, реконструкции или демонтаже.

3 – Нарушения при эксплуатации • Отсутствие технического мониторинга состояния конструкций или игнорирование его результатов; • Отсутствие профилактических ремонтов конструкций, восстановления антикоррозионных покрытий; • Перегрузка конструкций оборудованием, пылью; настилка новых конструктивных слоёв; • Непроектное приложение нагрузок (внеузловое нагружение ферм); искривление осей металлических стержневых элементов; • Создание условий для образования снеговых мешков на кровле; • Несанкционированные перепланировки, устройство непредусмотренных проектов проёмов в несущих конструкциях; снятие или перестановка связей; • Пролив агрессивных жидкостей (масел, кислот) на несущие конструкции; • Замачивание (атмосферной или технической влагой), промерзание грунтов основания; • Выемка грунта вблизи существующего фундамента; • Повышенная влажность в подвалах и техподпольях, приводящая к разрушению каменной кладки; • Засорение водостоков на кровлях; • Несвоевременная очистка кровель от снега.
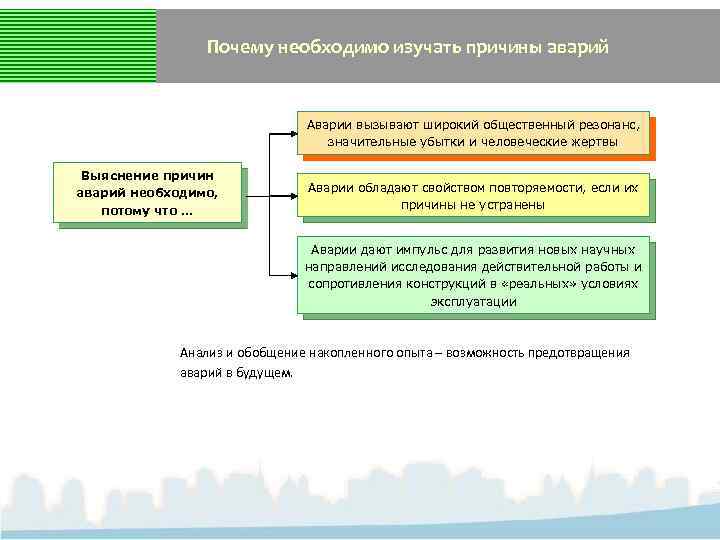
Почему необходимо изучать причины аварий Аварии вызывают широкий общественный резонанс, значительные убытки и человеческие жертвы Выяснение причин аварий необходимо, потому что … Аварии обладают свойством повторяемости, если их причины не устранены Аварии дают импульс для развития новых научных направлений исследования действительной работы и сопротивления конструкций в «реальных» условиях эксплуатации Анализ и обобщение накопленного опыта – возможность предотвращения аварий в будущем.

РАЗВИТИЕ МЕТОДОВ РАСЧЁТНОЙ ОЦЕНКИ БЕЗОПАСНОСТИ РАБОТЫ КОНСТРУКЦИИ
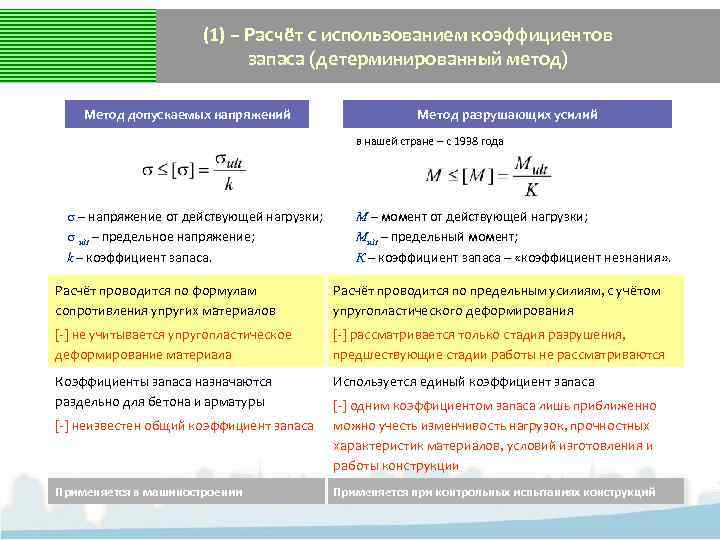
(1) – Расчёт с использованием коэффициентов запаса (детерминированный метод) Метод допускаемых напряжений Метод разрушающих усилий в нашей стране – с 1938 года – напряжение от действующей нагрузки; ult – предельное напряжение; k – коэффициент запаса. М – момент от действующей нагрузки; Mult – предельный момент; К – коэффициент запаса – «коэффициент незнания» . Расчёт проводится по формулам сопротивления упругих материалов Расчёт проводится по предельным усилиям, с учётом упругопластического деформирования [-] не учитывается упругопластическое деформирование материала [-] рассматривается только стадия разрушения, предшествующие стадии работы не рассматриваются Коэффициенты запаса назначаются раздельно для бетона и арматуры Используется единый коэффициент запаса [-] неизвестен общий коэффициент запаса Применяется в машиностроении [-] одним коэффициентом запаса лишь приближенно можно учесть изменчивость нагрузок, прочностных характеристик материалов, условий изготовления и работы конструкции Применяется при контрольных испытаниях конструкций

(2) – Расчёт с использованием частных коэффициентов надёжности (полувероятностный метод) Метод предельных состояний нормативная нагрузка коэффициент надёжности по нагрузке коэффициент сочетаний в нашей стране – с 1955 года геометрия сечения нормативное сопротивление коэффициент надёжности по материалу коэффициент надёжности по назначению Единый коэффициент запаса разделён на несколько частных коэффициентов надёжности [-] Метод является полувероятностным – не оценивается надёжность в явном виде, не учитывается фактор времени Применяется в качестве основного метода расчёта строительных конструкций и оснований в России и за рубежом коэффициент условий работы Расчётная нагрузка: Расчётное сопротивление:
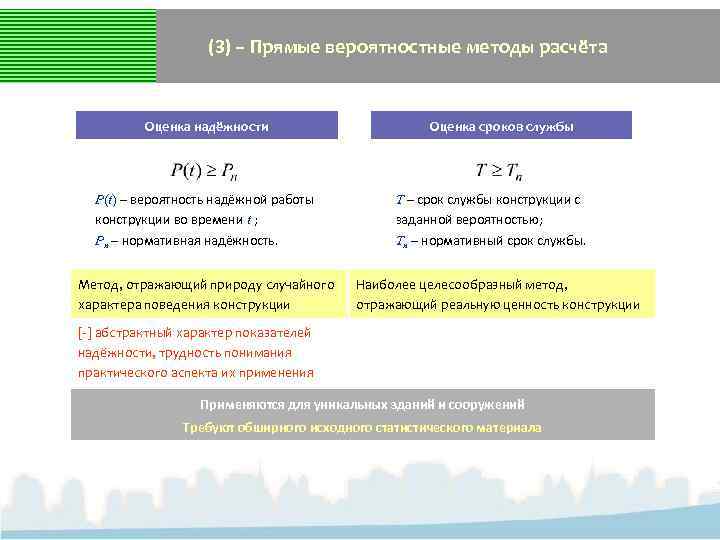
(3) – Прямые вероятностные методы расчёта Оценка надёжности P(t) – вероятность надёжной работы конструкции во времени t ; Pn – нормативная надёжность. Метод, отражающий природу случайного характера поведения конструкции Оценка сроков службы T – срок службы конструкции с заданной вероятностью; Tn – нормативный срок службы. Наиболее целесообразный метод, отражающий реальную ценность конструкции [-] абстрактный характер показателей надёжности, трудность понимания практического аспекта их применения Применяются для уникальных зданий и сооружений Требуют обширного исходного статистического материала
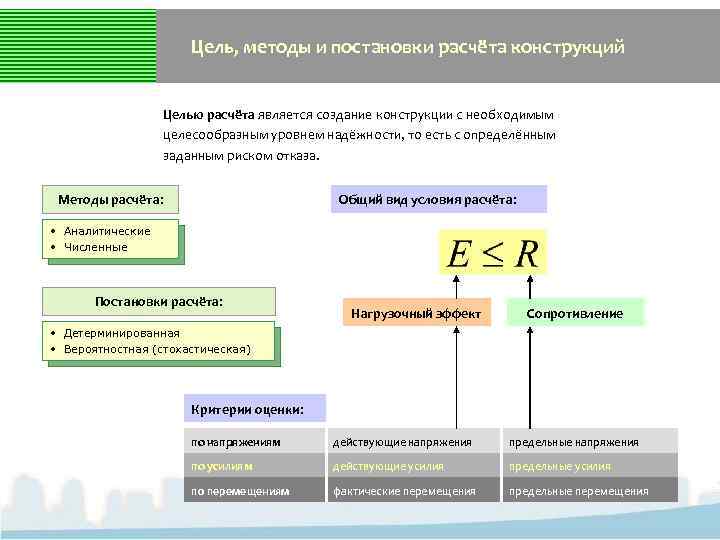
Цель, методы и постановки расчёта конструкций Целью расчёта является создание конструкции с необходимым целесообразным уровнем надёжности, то есть с определённым заданным риском отказа. Методы расчёта: Общий вид условия расчёта: • Аналитические • Численные Постановки расчёта: Нагрузочный эффект Сопротивление • Детерминированная • Вероятностная (стохастическая) Критерии оценки: по напряжениям действующие напряжения предельные напряжения по усилиям действующие усилия предельные усилия по перемещениям фактические перемещения предельные перемещения
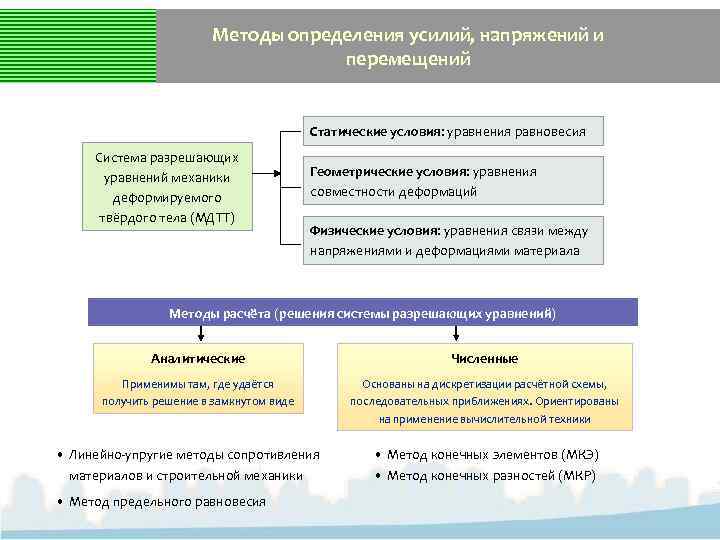
Методы определения усилий, напряжений и перемещений Статические условия: уравнения равновесия Система разрешающих уравнений механики деформируемого твёрдого тела (МДТТ) Геометрические условия: уравнения совместности деформаций Физические условия: уравнения связи между напряжениями и деформациями материала Методы расчёта (решения системы разрешающих уравнений) Аналитические Численные Применимы там, где удаётся получить решение в замкнутом виде Основаны на дискретизации расчётной схемы, последовательных приближениях. Ориентированы на применение вычислительной техники • Линейно-упругие методы сопротивления материалов и строительной механики • Метод предельного равновесия • Метод конечных элементов (МКЭ) • Метод конечных разностей (МКР)
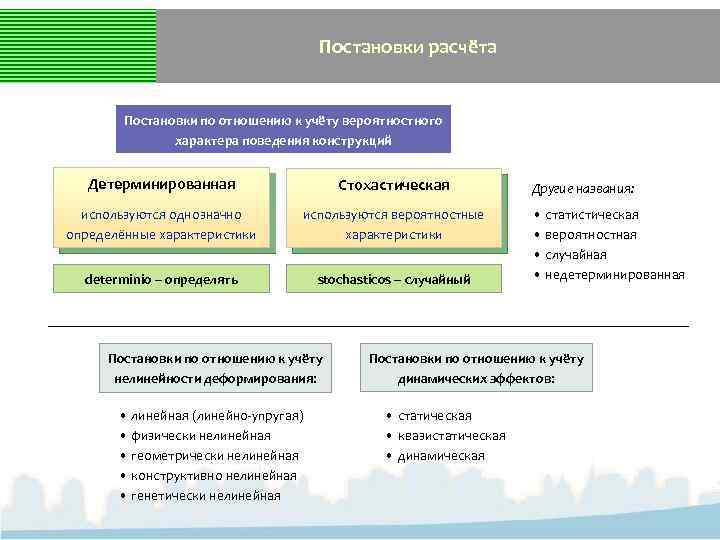
Постановки расчёта Постановки по отношению к учёту вероятностного характера поведения конструкций Детерминированная Стохастическая используются однозначно определённые характеристики используются вероятностные характеристики determinio – определять stochasticos – случайный Постановки по отношению к учёту нелинейности деформирования: • линейная (линейно-упругая) • физически нелинейная • геометрически нелинейная • конструктивно нелинейная • генетически нелинейная Другие названия: • статистическая • вероятностная • случайная • недетерминированная Постановки по отношению к учёту динамических эффектов: • статическая • квазистатическая • динамическая

Основные требования к несущим конструкциям по EN 1990 Конструкция должна быть спроектирована и выполнена таким образом, чтобы (1) на протяжении проектного срока службы с достаточной степенью надёжности и долговечности • могла воспринимать все воздействия, которые могут возникнуть во время строительства и эксплуатации; • могла выполнять свои функции; (2) обладала достаточной механической прочностью, эксплуатационной пригодностью и долговечностью; (3) сохраняла достаточную несущую способность в течение заданного времени при пожаре; (4) исключались непропорционально большие повреждения, вызванные аварийными ситуациями (взрыв, удар, ошибки деятельности человека). EN 1990, ст. 2. 1. 1(Р) – 2. 1. 4(Р)
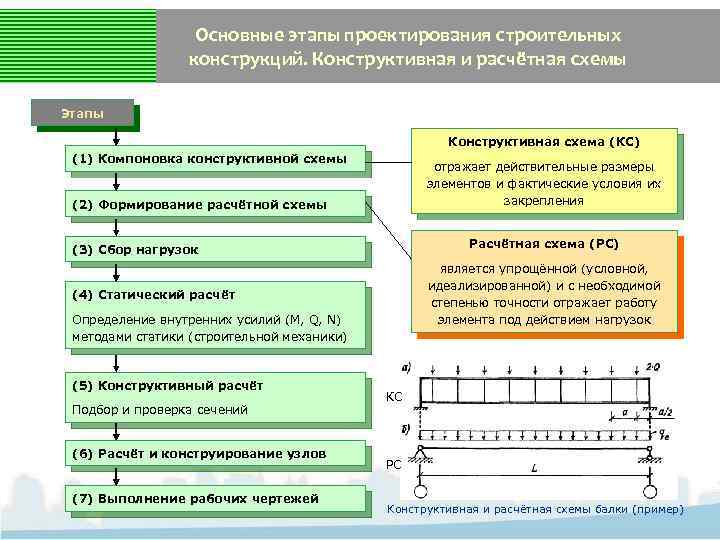
Основные этапы проектирования строительных конструкций. Конструктивная и расчётная схемы Этапы Конструктивная схема (КС) (1) Компоновка конструктивной схемы отражает действительные размеры элементов и фактические условия их закрепления (2) Формирование расчётной схемы Расчётная схема (РС) (3) Сбор нагрузок является упрощённой (условной, идеализированной) и с необходимой степенью точности отражает работу элемента под действием нагрузок (4) Статический расчёт Определение внутренних усилий (M, Q, N) методами статики (строительной механики) (5) Конструктивный расчёт Подбор и проверка сечений (6) Расчёт и конструирование узлов (7) Выполнение рабочих чертежей КС РС Конструктивная и расчётная схемы балки (пример)

ОСНОВЫ МЕТОДА ПРЕДЕЛЬНЫХ СОСТОЯНИЙ
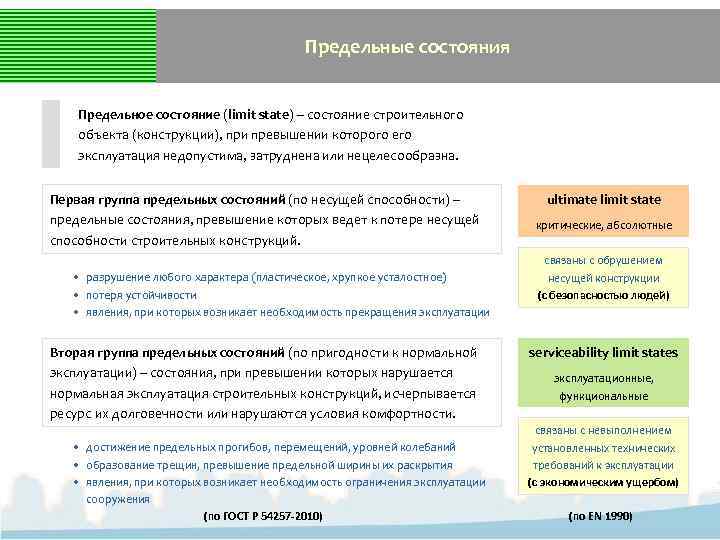
Предельные состояния Предельное состояние (limit state) – состояние строительного объекта (конструкции), при превышении которого его эксплуатация недопустима, затруднена или нецелесообразна. Первая группа предельных состояний (по несущей способности) – предельные состояния, превышение которых ведет к потере несущей способности строительных конструкций. • разрушение любого характера (пластическое, хрупкое усталостное) • потеря устойчивости • явления, при которых возникает необходимость прекращения эксплуатации Вторая группа предельных состояний (по пригодности к нормальной эксплуатации) – состояния, при превышении которых нарушается нормальная эксплуатация строительных конструкций, исчерпывается ресурс их долговечности или нарушаются условия комфортности. • достижение предельных прогибов, перемещений, уровней колебаний • образование трещин, превышение предельной ширины их раскрытия • явления, при которых возникает необходимость ограничения эксплуатации сооружения (по ГОСТ Р 54257 -2010) ultimate limit state критические, абсолютные связаны с обрушением несущей конструкции (с безопасностью людей) serviceability limit states эксплуатационные, функциональные связаны с невыполнением установленных технических требований к эксплуатации (с экономическим ущербом) (по EN 1990)

Предельные состояния по EN 1990 Предельные состояния (limit state) – состояния, при превышении которых конструкция перестаёт соответствовать установленным расчётным критериям. EN 1990, ст. 1. 5. 2. 12 Расчётные критерии (design criteria) – количественные условия, которые должны быть выполнены для каждого предельного состояния. EN 1990, ст. 1. 5. 2. 1 ULS – Критические (абсолютные) предельные состояния (ultimate limit state) – состояния, связанные с обрушением или с другими подобными формами разрушения несущей конструкции. EN 1990, ст. 1. 5. 2. 13 связаны с безопасностью людей SLS – Эксплуатационные (функциональные) предельные состояния (serviceability limit states) – состояния, при превышении которых не выполняются установленные технические требования к эксплуатации сооружения или их элементов. связаны с экономическим ущербом конструкция сохраняет возможность выполнять свою функцию EN 1990, ст. 1. 5. 2. 14

Расчётные ситуации – учитываемый при расчёте сооружений комплекс наиболее неблагоприятных условий, которые могут возникнуть при его эксплуатации и возведении. Виды расчётных ситуаций: • установившаяся – ситуация, имеющая продолжительность, близкую к сроку службы строительного объекта (например, эксплуатация между двумя капитальными ремонтами или изменениями технологического процесса); • переходная – ситуация, имеющая продолжительность, небольшую по сравнению со сроком службы строительного объекта (например, изготовление, транспортирование, монтаж, капитальный ремонт и реконструкция строительного объекта); • аварийная – ситуация, соответствующая исключительным условиям работы сооружения (в том числе и при особых воздействиях), которые могут привести к существенным социальным, экологическим и экономическим потерям.

Нормативные и расчётные нагрузки Основными характеристиками нагрузок являются их нормативные значения qn , устанавливаемые нормами проектирования или заданием на проектирование. Нормативные нагрузки соответствуют условиям нормальной эксплуатации сооружений. Расчетное значение нагрузки q – это результат умножения нормативного значения на коэффициент надежности по нагрузке. qn – нормативная нагрузка; q – расчётная нагрузка; f – коэффициент надёжности по нагрузке. Расчётные нагрузки используются в расчётах конструкций по предельным состояниям. Коэффициент надежности по нагрузке f учитывает возможное отклонение нагрузок в неблагоприятную (большую или меньшую) сторону от их нормативных значений. Как правило, неблагоприятным является отклонение в большую сторону ( f > 1).

Нормативные и расчётные сопротивления Основными характеристиками прочности материалов, используемые при проектировании, являются их нормативные сопротивления Rn , назначаемые на основе результатов испытаний стандартных образцов. Нормативные значения прочностных характеристик материалов устанавливаются в нормативных документах или технических условиях (ТУ) и контролируются при изготовлении конструкций, строительстве и эксплуатации строительного объекта. Rn – нормативное сопротивление; R – расчётное сопротивление; m – коэффициент надёжности по материалу. Расчётное сопротивление R – это результат деления нормативного сопротивления на коэффициент надежности по материалу. Расчётные сопротивления используются в расчётах конструкций по предельным состояниям. Коэффициент надёжности по материалу m учитывает возможное отклонение прочностных характеристик материалов в неблагоприятную (меньшую) сторону от их нормативных значений. Для металлических конструкций коэффициент m учитывает также установленные допуски на размеры сечений проката.
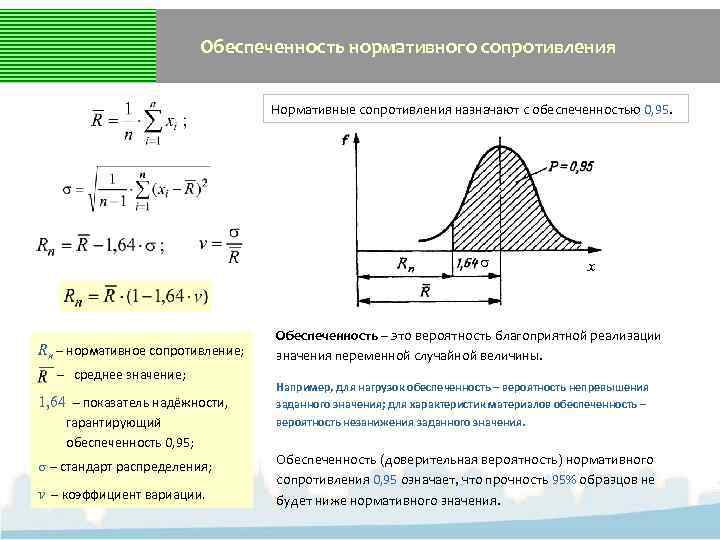
Обеспеченность нормативного сопротивления Нормативные сопротивления назначают с обеспеченностью 0, 95. Rn – нормативное сопротивление; – среднее значение; 1, 64 – показатель надёжности, гарантирующий обеспеченность 0, 95; – стандарт распределения; v – коэффициент вариации. х Обеспеченность – это вероятность благоприятной реализации значения переменной случайной величины. Например, для нагрузок обеспеченность – вероятность непревышения заданного значения; для характеристик материалов обеспеченность – вероятность незанижения заданного значения. Обеспеченность (доверительная вероятность) нормативного сопротивления 0, 95 означает, что прочность 95% образцов не будет ниже нормативного значения.
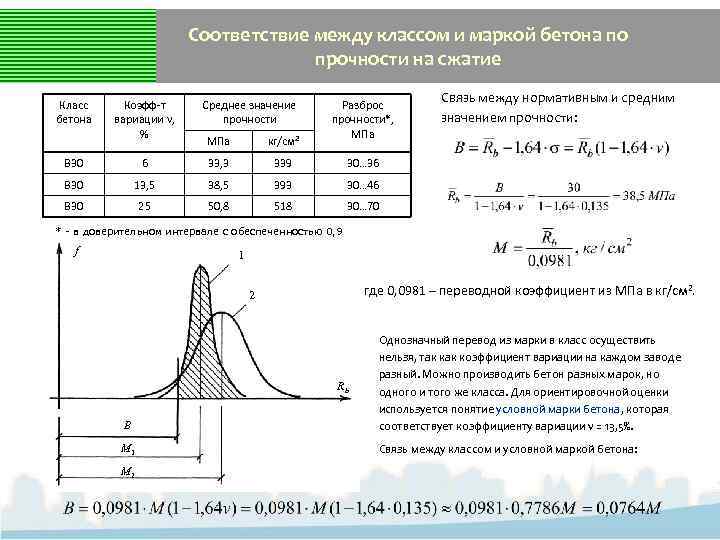
Соответствие между классом и маркой бетона по прочности на сжатие Класс бетона Коэфф-т вариации v, % Среднее значение прочности МПа кг/см 2 Разброс прочности*, МПа В 30 6 33, 3 339 30… 36 В 30 13, 5 38, 5 393 30… 46 В 30 25 50, 8 518 Связь между нормативным и средним значением прочности: 30… 70 * - в доверительном интервале с обеспеченностью 0, 9 f 1 где 0, 0981 – переводной коэффициент из МПа в кг/см 2. 2 В Однозначный перевод из марки в класс осуществить нельзя, так коэффициент вариации на каждом заводе разный. Можно производить бетон разных марок, но одного и того же класса. Для ориентировочной оценки используется понятие условной марки бетона, которая соответствует коэффициенту вариации v = 13, 5%. М 1 Связь между классом и условной маркой бетона: Rb М 2

НАГРУЗКИ И ВОЗДЕЙСТВИЯ
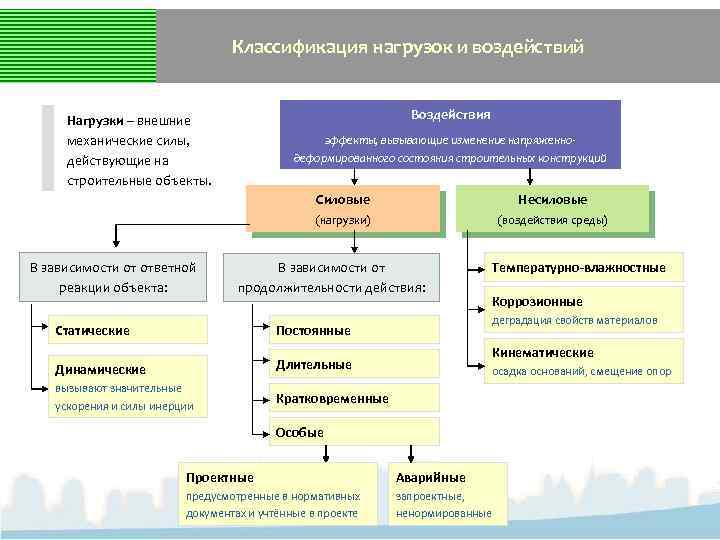
Классификация нагрузок и воздействий Воздействия Нагрузки – внешние механические силы, действующие на строительные объекты. эффекты, вызывающие изменение напряженнодеформированного состояния строительных конструкций Силовые (нагрузки) В зависимости от ответной реакции объекта: Несиловые (воздействия среды) В зависимости от продолжительности действия: Статические Длительные вызывают значительные ускорения и силы инерции Коррозионные деградация свойств материалов Постоянные Динамические Температурно-влажностные Кратковременные Кинематические осадка оснований, смещение опор Особые Проектные Аварийные предусмотренные в нормативных документах и учтённые в проекте запроектные, ненормированные

Виды нагрузок Постоянные – нагрузки, изменение расчетных значений которых в течение расчетного срока службы строительного объекта пренебрежимо мало по сравнению с их средними значениями • Собственный вес конструкций • Вес и давление грунтов • Усилия от предварительного напряжения Длительные – нагрузки, сохраняющие расчетные значения во время эксплуатации длительное время • • Вес временных перегородок Вес стационарного оборудования Вес складируемых материалов Пониженные нормативные значения нагрузок от людей, оборудования, мостовых и подвесных кранов, снега ГОСТ Р 54257 -2010. Надёжность … СП 20. 13330. 2011. Нагрузки и воздействия Кратковременные – нагрузки, длительность действия расчетных значений которых существенно меньше срока службы сооружения • Ветровая нагрузка • Полные нормативные значения нагрузок от людей, оборудования, мостовых и подвесных кранов, снега • Нагрузка от транспортных средств Особые – нагрузки, имеющие малую вероятность появления и небольшую продолжительность, но создающие чрезвычайные ситуации с возможными катастрофическими последствиями • • Сейсмические воздействия Воздействия взрывов Воздействия, обусловленные пожаром Воздействия, вызванные столкновениями с движущимися транспортными средствами • Карстовые воронки • Отказы отдельных несущих элементов

Нормативное значение постоянного воздействия Если изменчивость постоянного воздействия невелика (коэффициент вариации V 0, 05… 0, 10), в качестве нормативного Gk можно использовать среднее значение. Если изменчивость значительна, или если конструкция является весьма чувствительной к изменениям G, используют верхнее и нижнее значения: Gk, inf (0, 05 квантиль) Gk, sup (0, 95 квантиль) Собственный вес обычно рассчитывается на основе номинальных размеров и средней удельной массы (Gk является средней величиной G). Коэффициент вариации VG 0, 02… 0, 05 Собственный вес подчиняется нормальному (Гауссовому) распределению: при VG = 0, 1 (10%) нижнее Gk, inf и верхнее Gk, sup значения будут на 16, 4% больше и меньше средней величины G

Нормативное значение временного воздействия В случае статистической обработки в качестве нормативного Qk принимается верхнее значение с заданной вероятностью превышения (р) в течение установленного отрезка времени (базового периода), например, в течение года ( = 1 год). Базовый период (reference period) – промежуток времени, выбранный для оценки статистических временных, и возможно, аварийных воздействий. Период повторяемости (Т) – ожидаемый промежуток времени между двумя последовательными повторениями характеристической величины, соответствующий вероятности p t – базовый период (1 год); p – вероятность превышения (2%). Вероятность непревышения (обеспеченность) Вероятность превышения Период повторяемости Число повторений за 50 лет 0, 98 0, 02 1/0, 02 = 50 лет 50/50 = 1 раз 0, 96 0, 04 1/0, 04 = 25 лет 50/25 = 2 раза 0, 93 0, 07 1/0, 07 = 15 лет 0, 92 0, 08 1/0, 08 = 12, 5 лет 50/12, 5 = 4 раза 0, 90 0, 10 1/0, 10 = 10 лет 50/10 = 5 раз EN 1990, ст. 1. 5. 3. 15
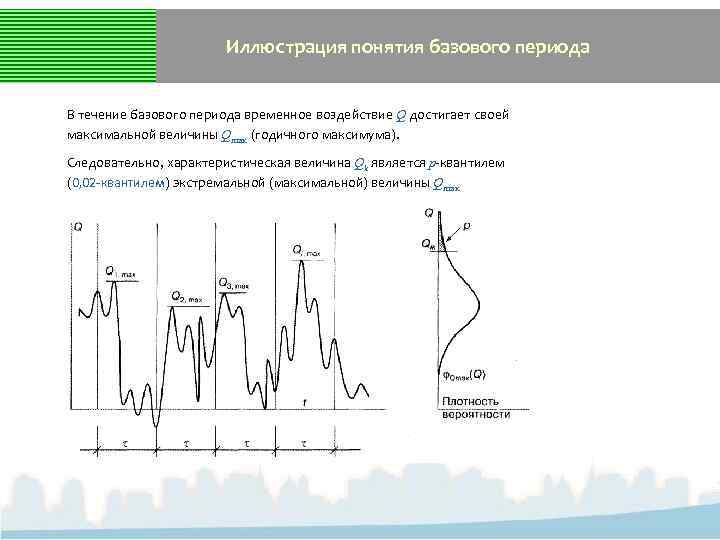
Иллюстрация понятия базового периода В течение базового периода временное воздействие Q достигает своей максимальной величины Qmax (годичного максимума). Следовательно, характеристическая величина Qk является р-квантилем (0, 02 -квантилем) экстремальной (максимальной) величины Qmax

Сочетания нагрузок (СНи. П 2. 01. 07 -85* ) На конструкцию действует, как правило, несколько нагрузок, и при расчёте необходимо выявить их наиболее неблагоприятное сочетание. При учёте одновременного действия более двух нагрузок их расчётные значения умножают на коэффициенты сочетаний < 1. Коэффициент сочетаний учитывает маловероятность одновременного действия максимальных значений нескольких нагрузок. СНи. П 2. 01. 07 -85* предусматривает основные и особые сочетания нагрузок: Сочетание Учитываемые нагрузки Коэффициенты сочетаний для нагрузок постоянных длительных кратковременных особых Основное 1 Постоянная + одна временная 1 1 1 - Основное 2 Постоянная + две и более временных 1 0, 95 0, 9 - Особое Постоянная + временные + одна особая 1 0, 95 0, 8 1 Сейсмич. * Постоянная + временные + сейсмич. 0, 9 0, 8 0, 5 1 * по СНи. П Строительство в сейсмических районах
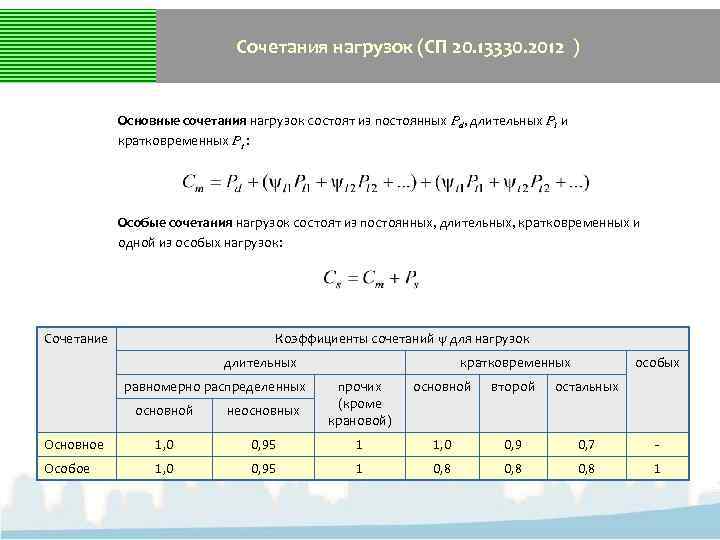
Сочетания нагрузок (СП 20. 13330. 2012 ) Основные сочетания нагрузок состоят из постоянных Pd, длительных Pl и кратковременных Pt : Особые сочетания нагрузок состоят из постоянных, длительных, кратковременных и одной из особых нагрузок: Коэффициенты сочетаний для нагрузок Сочетание длительных равномерно распределенных кратковременных особых прочих (кроме крановой) основной второй остальных основной неосновных Основное 1, 0 0, 95 1 1, 0 0, 9 0, 7 - Особое 1, 0 0, 95 1 0, 8 1

ОСНОВНЫЕ СВЕДЕНИЯ О СЛУЧАЙНЫХ ВЕЛИЧИНАХ

Случайные события и величины (1) Случайное событие – это такое событие, которое при неоднократном воспроизведении одного и того же опыта каждый раз протекает по-иному. Под событием в теории вероятностей принимается всякий факт, который может произойти, а может и не произойти. (2) Случайная величина – это величина, которая может принимать то или иное значение в зависимости от степени воздействия на нее случайных факторов. Например, прогибы двух совершенно одинаковых балок при одной и той же нагрузке. Прогибы будут отличаться вследствие различной степени уплотнения бетона, изменения положения арматуры по высоте сечения и условий сцепления арматуры с бетоном, дефектов изготовления и других факторов, которые однозначно нельзя предсказать заранее то есть всегда существует некоторая неопределённость (3) Вероятность случайного события – это отношение количества интересующих нас результатов к их общему количеству. Например, на складе имеется 50 панелей перекрытий и одна из них дефектная. Какова вероятность того, что первая взятая панель будет дефектной?

Дискретные и непрерывные случайные величины (1) Дискретная случайная величина принимает только отдельные, изолированные возможные значения с определенными вероятностями. Примеры дискретных случайных величин: • число циклов повторной нагрузки до разрушения конструкции; (2) Непрерывная случайная величина принимает любые значения из непрерывного числового множества в промежутке между предельными значениями. Примеры непрерывных случайных величин: • предел текучести стали С 245 • число дефектных изделий (панелей) в партии. • прочность на сжатие бетона класса В 30 • срок службы склада противогололёдных реагентов • ширина раскрытия трещин (ШРТ) в железобетоне

Функция распределения случайной величины Функция распределения F(x) (или интегральная функция) определяет вероятность того, что случайная величина примет значение меньше x: – значение случайной величины; х – текущее значение. Свойства функции распределения: • неубывающая функция; • безразмерная, изменяется в пределах от 0 до 1. Функция распределения является наиболее универсальной характеристикой как непрерывных, так и дискретных случайных величин.

Плотность распределения непрерывной случайной величины Плотность распределения f (x) – это первая производная от интегральной функции распределения. (плотность вероятности, или дифференциальная функция) Свойства плотности распределения: • неотрицательная функция; • имеет размерность, обратную размерности случайной величины: • площадь, ограниченная кривой и горизонтальной осью, равна 1: Вероятность попадания случайной величины в интервал (х1 … х2) равна заштрихованной площади под кривой плотности распределения:

Числовые характеристики случайных величин Для дискретных случайных величин Для непрерывных случайных величин (1) Математические ожидание – это средневзвешенное значение данной случайной величины, вокруг которого группируются все её возможные значения. Это характеристика положения случайной величины на числовой оси. Pi – вероятность значения xi f(x) – плотность вероятности (2) Дисперсия характеризует разброс значений случайной величины вокруг математического ожидания. Это характеристика рассеивания. (3) Среднеквадратическое отклонение (СКО), или стандарт случайной величины: (4) Коэффициент вариации характеризует рассеивание в относительной форме: (5) Другие характеристики: Имеет размерность случайной величины. мода, медиана, начальные и центральные моменты, асимметрия, эксцесс
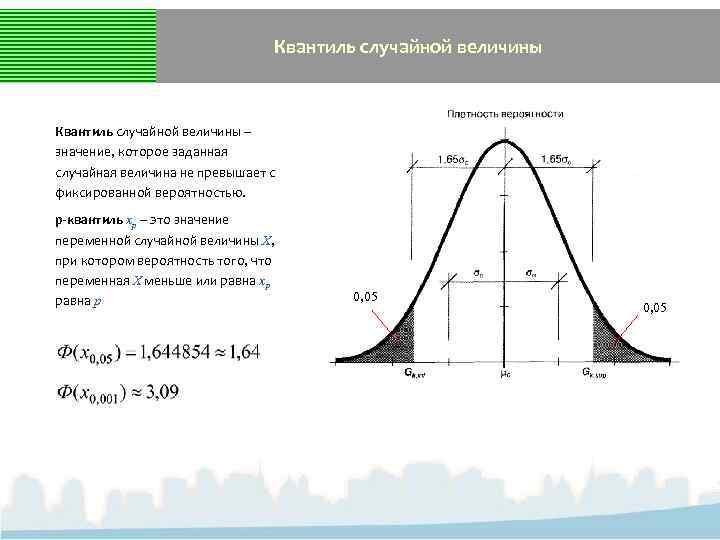
Квантиль случайной величины – значение, которое заданная случайная величина не превышает с фиксированной вероятностью. р-квантиль хр – это значение переменной случайной величины Х, при котором вероятность того, что переменная Х меньше или равна хр равна р 0, 05

Нормальное распределение (закон Гаусса) (1) Историческая справка: Этот своеобразный закон был введен в рассмотрение Муавром (1667 -1754) и получил более общее обоснование у Гаусса (1777 -1855). (2) Плотность нормального распределения a – математическое ожидание; – стандарт.

Применение нормального распределения в строительстве (1) Центральная предельная теорема Распределению Гаусса подчиняются случайные величины, отклонения которых вызваны большим количеством случайных факторов, каждый из которых в отдельности незначителен. (2) Сумма большого количества независимых случайных величин подчиняется нормальному закону, и тем точнее, чем больше величин суммируется. Важно только, чтобы все суммируемые ошибки равномерно играли в общей сумме относительно малую роль. (3) Примеры величин, подчиняющихся нормальному закону распределения: • ошибки (погрешности) измерений; • отклонения геометрических размеров конструкций; • механические характеристики материалов; • некоторые нагрузки.

Интеграл вероятностей Интегральная функция нормального распределения: Интеграл вида не выражается через элементарные функции и задаётся в виде таблиц значений специальной функции В итоге: где u – квантиль; Ф(u) – функция Лапласа (интеграл вероятностей). Свойства функции Лапласа:
Надёжность.ppt