Начертательная геометрия Тема 9 Пересечение поверхностей Метод сфер

Начертательная геометрия Тема 9 Пересечение поверхностей. Метод сфер. Цель: сформировать представление о применимости метода сфер для определения линии пересечения поверхностей

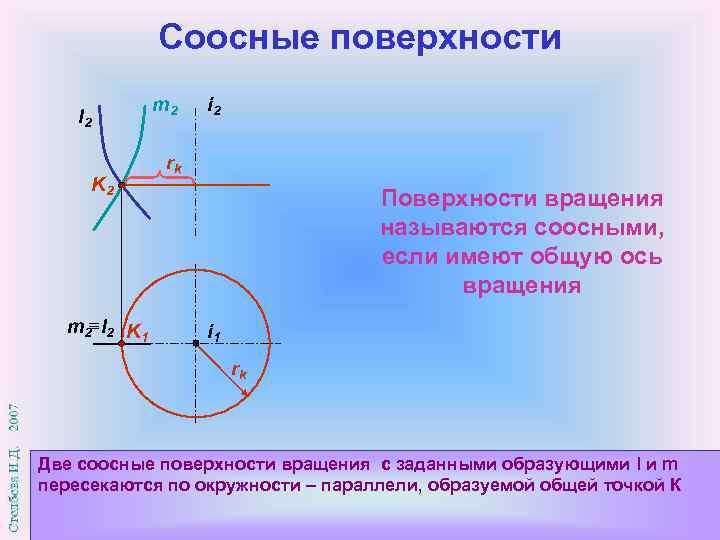Соосные поверхности m 2 l 2 K 2 m 2 l 2 K 1 i 2 rk Поверхности вращения называются соосными, если имеют общую ось вращения i 1 rk Две соосные поверхности вращения с заданными образующими l и m пересекаются по окружности – параллели, образуемой общей точкой К

Сфера, соосная с конусом и цилиндром m 2 i 2 1 12 l 2 О 2 22 m 2 l 2 (21) i 2 2 11 i 1 22 О 2 1. Центр соосной сферы лежит на оси поверхности вращения 2. Соосная сфера пересекает поверхность вращения по окружности Соосные поверхности вращения (сфера и конус; сфера и цилиндр) пересекаются по окружностям – параллелям, образуемым общими точками 1 и 2. На П 2 параллели проецируются в прямые, перпендикулярные общей оси вращения i.

Условия применимости метода сфер • Заданы две поверхности вращения • Оси вращения поверхностей пересекаются в точке • Оси вращения поверхностей должны быть параллельны одной из плоскостей проекций, чтобы их параллели-окружности проецировались в виде отрезкадиаметра

12. ПО 12 a 2 с2 (d 2) b 2 О 2 22 d 1 11 (21) a 1 b 1 Ф 1 c 1 Поверхности имеют общую плоскость симметрии Ф(Ф 1), являющейся фронтальной плоскостью уровня. Следовательно, на П 2 можно зафиксировать проекции опорных точек искомой линии 12 и 22 как пересечение очерков поверхностей. Проекции 11 и 21 располагаем на Ф 1.

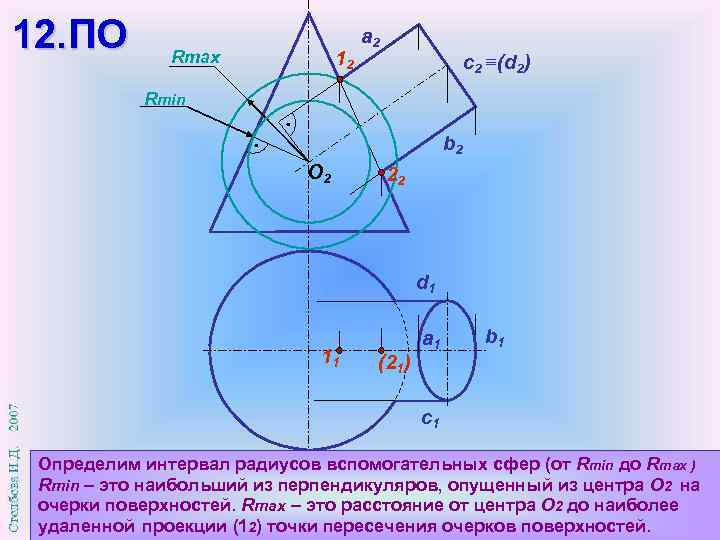12. ПО Rmax 12 a 2 с2 (d 2) Rmin b 2 О 2 22 d 1 11 (21) a 1 b 1 c 1 Определим интервал радиусов вспомогательных сфер (от Rmin до Rmax ) Rmin – это наибольший из перпендикуляров, опущенный из центра О 2 на очерки поверхностей. Rmax – это расстояние от центра О 2 до наиболее удаленной проекции (12) точки пересечения очерков поверхностей.

12. ПО 12 Rmax С 2 Rmin i 2 a 2 32 (42) В 2 b 2 А 2 О 2 с2 (d 2) D 2 22 11 31 О 2 d 1 41 А 1 i 2 В 1 (21) a 1 b 1 c 1 Определим точки линии с помощью сферы Rmin , которая пересекается с цилиндром и касается конуса по соответствующим параллелям. Пересечение отрезков (проекций параллелей) А 2 В 2 и С 2 Д 2 дает на П 2 проекции двух совпадающих точек 32 и 42. Проекции 31 и 41 располагаем на

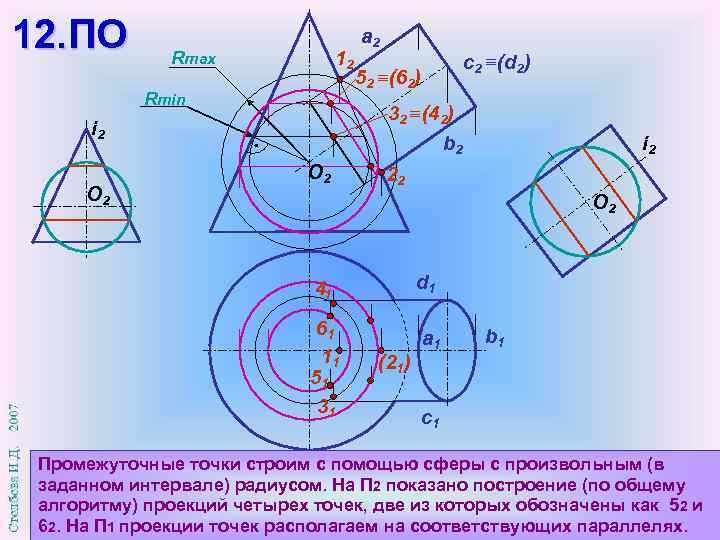12. ПО 12 Rmax Rmin с2 (d 2) 52 (62) 32 (42) b 2 i 2 О 2 a 2 О 2 i 2 22 О 2 d 1 41 61 11 51 31 (21) a 1 b 1 c 1 Промежуточные точки строим с помощью сферы с произвольным (в заданном интервале) радиусом. На П 2 показано построение (по общему алгоритму) проекций четырех точек, две из которых обозначены как 5 2 и 62. На П 1 проекции точек располагаем на соответствующих параллелях.

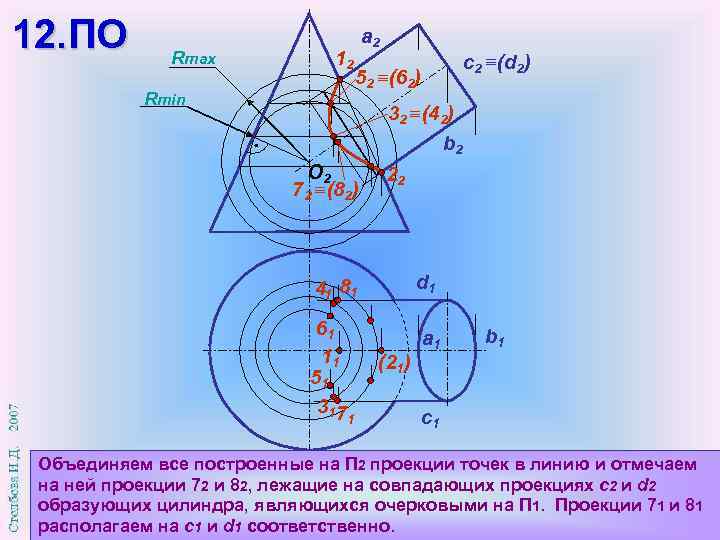12. ПО Rmax 12 Rmin a 2 с2 (d 2) 52 (62) 32 (42) b 2 О 2 72 (82) 22 d 1 41 81 61 11 51 317 (21) 1 a 1 b 1 c 1 Объединяем все построенные на П 2 проекции точек в линию и отмечаем на ней проекции 72 и 82, лежащие на совпадающих проекциях с2 и d 2 образующих цилиндра, являющихся очерковыми на П 1. Проекции 71 и 81 располагаем на с1 и d 1 соответственно.

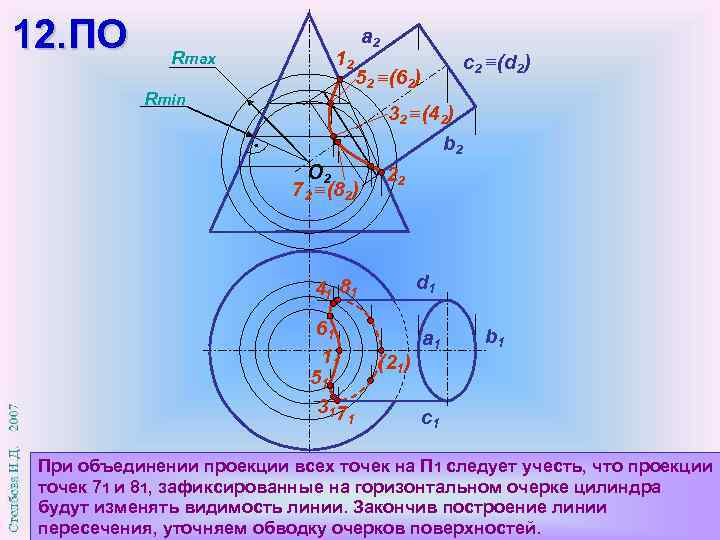12. ПО Rmax 12 Rmin a 2 с2 (d 2) 52 (62) 32 (42) b 2 О 2 72 (82) 22 d 1 41 81 61 11 51 317 (21) 1 a 1 b 1 c 1 При объединении проекции всех точек на П 1 следует учесть, что проекции точек 71 и 81, зафиксированные на горизонтальном очерке цилиндра будут изменять видимость линии. Закончив построение линии пересечения, уточняем обводку очерков поверхностей.

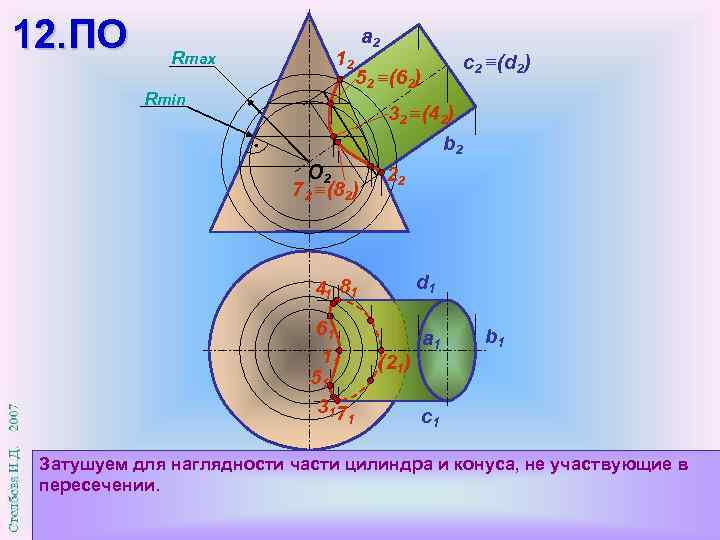12. ПО Rmax 12 Rmin a 2 с2 (d 2) 52 (62) 32 (42) b 2 О 2 72 (82) 22 d 1 41 81 61 11 51 317 (21) 1 a 1 b 1 c 1 Затушуем для наглядности части цилиндра и конуса, не участвующие в пересечении.

Теорема Монжа Если две поверхности второго порядка описаны около третьей или вписаны в нее, то они пересекаются между собой по двум плоским кривым второго порядка

13. ПО a 2 с2 (d 2) b 2 d 1 а 1 (b 1) c 1 В пересекающиеся поверхности вращения вписывается общая сфера. Следовательно, при построении линии пересечения заданных поверхностей можно использовать теорему Монжа.

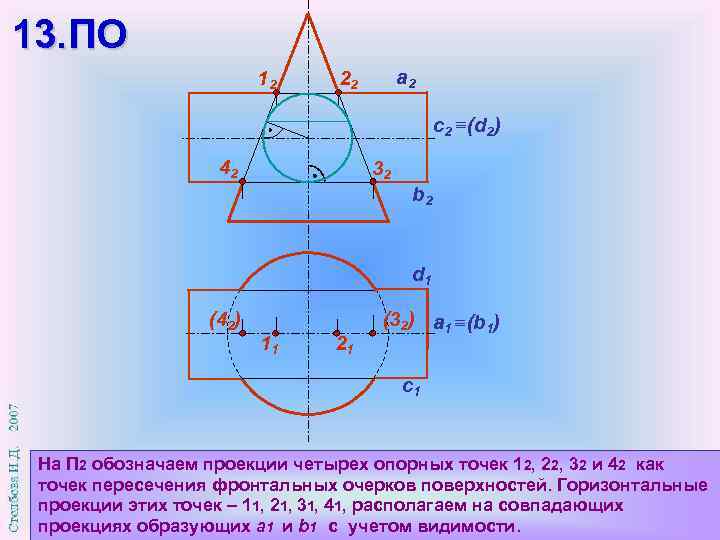13. ПО 12 a 2 22 с2 (d 2) 42 32 b 2 d 1 (42) 11 21 (32) а 1 (b 1) c 1 На П 2 обозначаем проекции четырех опорных точек 12, 22, 32 и 42 как точек пересечения фронтальных очерков поверхностей. Горизонтальные проекции этих точек – 11, 21, 31, 41, располагаем на совпадающих проекциях образующих а 1 и b 1 с учетом видимости.

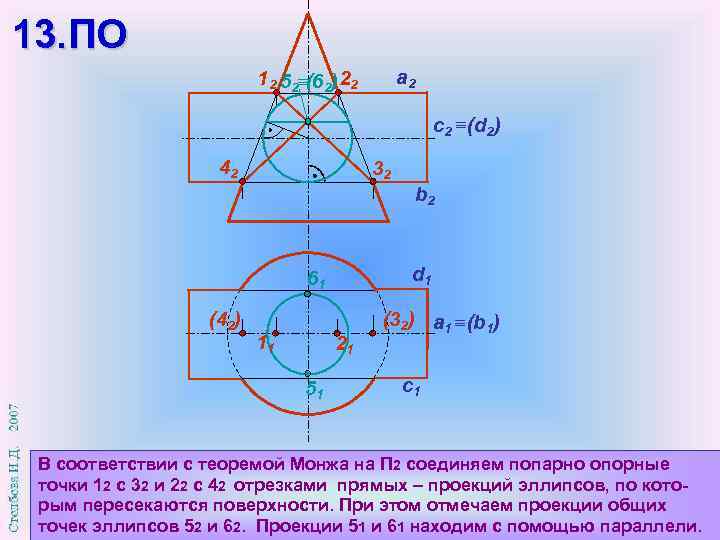13. ПО a 2 12 52 (62) 22 с2 (d 2) 42 32 b 2 d 1 61 (42) 11 21 51 (32) а 1 (b 1) c 1 В соответствии с теоремой Монжа на П 2 соединяем попарно опорные точки 12 с 32 и 22 с 42 отрезками прямых – проекций эллипсов, по которым пересекаются поверхности. При этом отмечаем проекции общих точек эллипсов 52 и 62. Проекции 51 и 61 находим с помощью параллели.

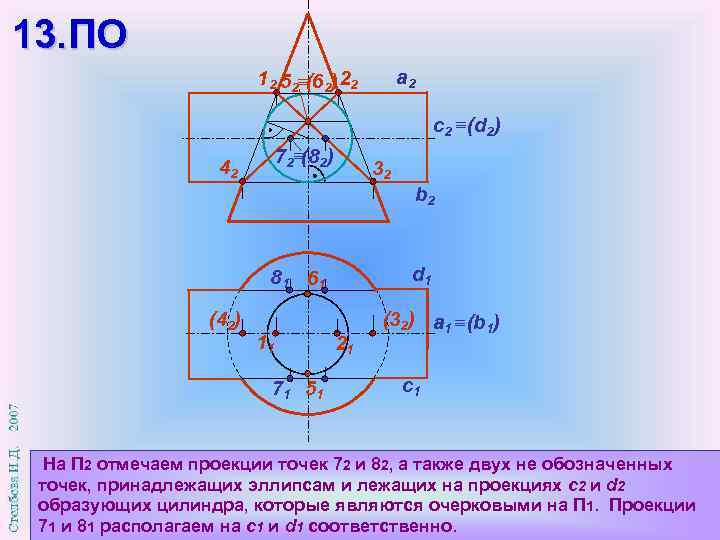13. ПО a 2 12 52 (62) 22 с2 (d 2) 72 (82) 42 32 b 2 d 1 81 61 (42) 11 71 51 21 (32) а 1 (b 1) c 1 На П 2 отмечаем проекции точек 72 и 82, а также двух не обозначенных точек, принадлежащих эллипсам и лежащих на проекциях с2 и d 2 образующих цилиндра, которые являются очерковыми на П 1. Проекции 71 и 81 располагаем на с1 и d 1 соответственно.

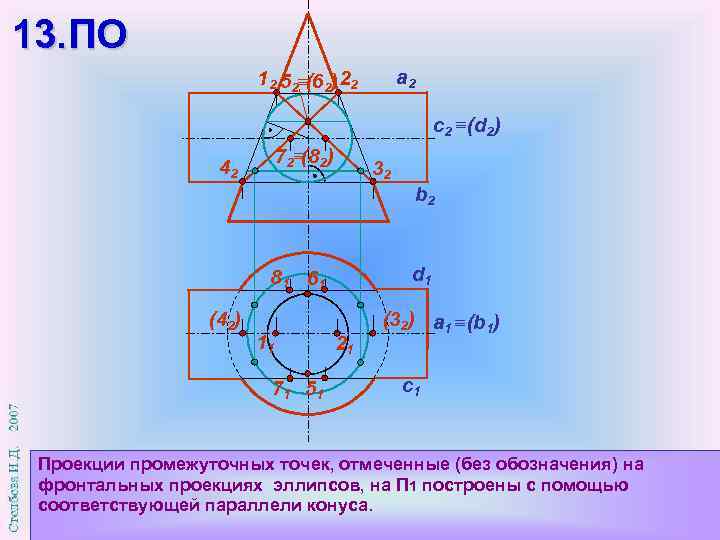13. ПО a 2 12 52 (62) 22 с2 (d 2) 72 (82) 42 32 b 2 d 1 81 61 (42) 11 71 51 21 (32) а 1 (b 1) c 1 Проекции промежуточных точек, отмеченные (без обозначения) на фронтальных проекциях эллипсов, на П 1 построены с помощью соответствующей параллели конуса.

13. ПО a 2 12 52 (62) 22 с2 (d 2) 72 (82) 42 32 b 2 d 1 81 61 (42) 11 71 51 21 (32) а 1 (b 1) c 1 Объединяем проекции всех построенных на П 1 точек в эллипсы, составляющие линию пересечения поверхностей. При этом, следует учесть, что проекции точек 71 и 81 (и пары не обозначенных точек), лежащих на горизонтальном очерке цилиндра, будут изменять видимость эллипсов.

13. ПО a 2 12 52 (62) 22 с2 (d 2) 72 (82) 42 32 b 2 d 1 81 61 (42) 11 71 51 21 (32) а 1 (b 1) c 1 Уточнив видимость очерков пересекающихся поверхностей, затушуем для наглядности части цилиндра и конуса, не участвующие в пересечении.

Задания в тестовой форме 1. Поверхности, которые могут занимать проецирующее положение … а) призматическая б) цилиндрическая в) поверхность вращения г) циклическая 2. Точки линии пересечения поверхностей, которые относятся к опорным … а) экстремальные точки б) точки видимости в) промежуточные точки г) характерные точки закономерных кривых 3. Общая плоскость симметрии двух пересекающихся поверхностей вращения проходит через … а) оси вращения б) экваторы в) очерки

Задания в тестовой форме 4. Условие, необходимое для получения соосных поверхностей … а) общее основание б) общая плоскость симметрии в) общая ось вращения 5. Радиус минимальной секущей сферы равен … а) наибольшей из нормалей к очеркам поверхностей б) наименьшей из нормалей к очеркам поверхностей в) экватору максимальной секущей сферы 6. Центр секущих концентрических сфер находится … а) в точке пересечения осей вращения б) на параллели минимальной сферы в) на экваторе наибольшей поверхности 7. Концентрические сферы –посредники следует применять, если оси поверхностей вращения пересекаются, а их общая плоскость симметрии … плоскости проекций. а) параллельна б) перпендикулярна

Задания в тестовой форме 8. Условие, необходимое для применения теоремы Монжа … а) одна из заданных поверхностей проецирующая б) заданные поверхности описаны около третьей в) заданные поверхности имеют общее основание 9. Концентрические сферы-посредники следует применять, если оси поверхностей вращения пересекаются, а их общая плоскость симметрии ____ плоскости проекций. 10. Если две поверхности второго порядка касаются друга в двух точках, то линия их пересечения распадается на две ____ кривые второго порядка.