Начертательная геометрия 1 семестр Изучение теории графических

Начертательная геометрия 1 семестр

Изучение теории графических изображений преследует три основные цели: • Освоение методов построения на плоскости изображений пространственных форм. • Исследование геометрических свойств фигур и тел по их изображениям • Развитие пространственного воображения

Содержание курса • Ортогональные проекции точки, прямой, плоскости. • Методы преобразования проекций. • Кривые линии и поверхности. • Пересечение поверхности плоскостью и прямой линией. • Взаимное пересечение поверхностей. • Развертки поверхностей.

Лекция 1 • Виды проецирования. • Образование комплексного чертежа. • Точка. Проекции точки. Конкурирующие точки. • Прямая. Образование прямой линии. Прямые уровня. Проецирующие прямые. • Признак принадлежности точки – прямой.

Символы и обозначения графических элементов

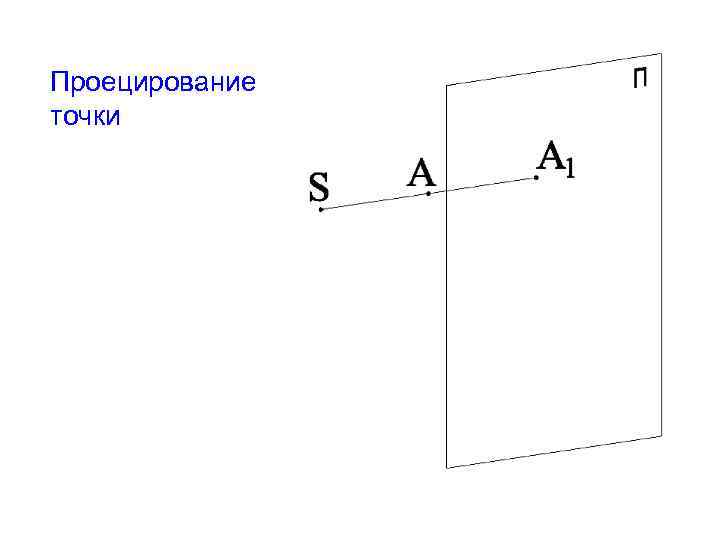Проецирование точки

Виды проецирования. Центральное (коническое) проецирование.

Центральное проецирование

Виды проецирования. Параллельное косоугольное проецирование

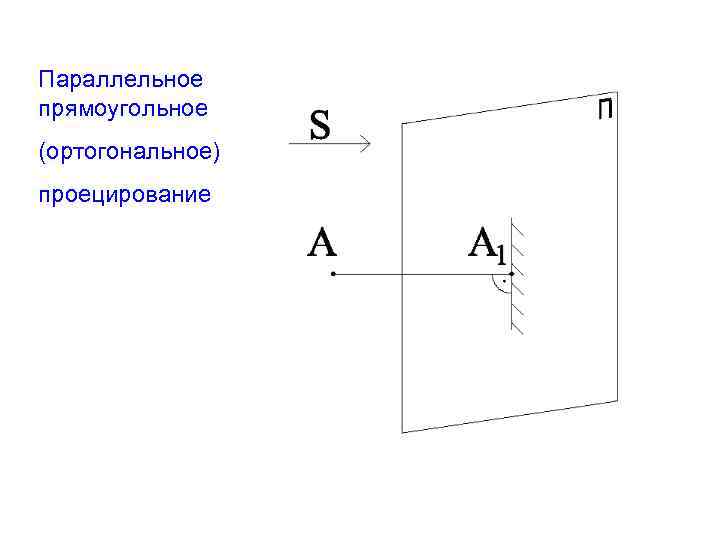Параллельное прямоугольное (ортогональное) проецирование

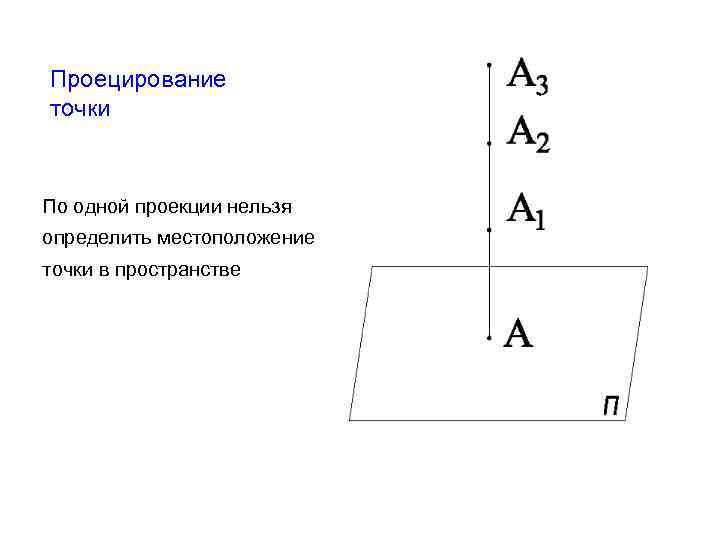Проецирование точки По одной проекции нельзя определить местоположение точки в пространстве

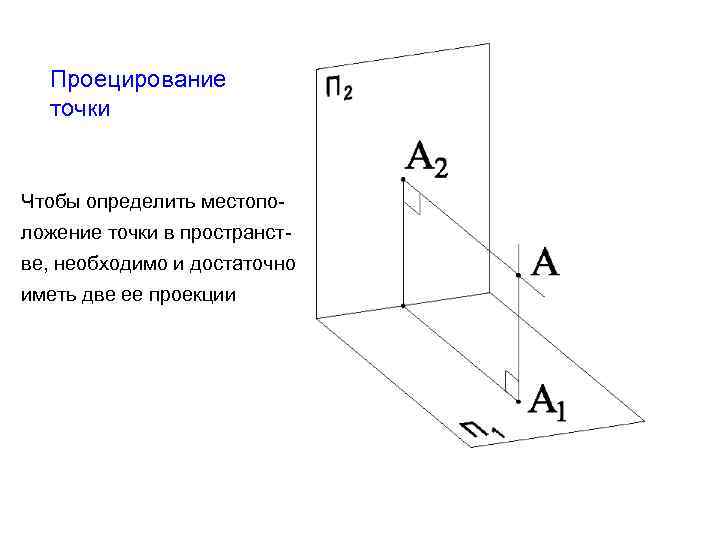Проецирование точки Чтобы определить местоположение точки в пространстве, необходимо и достаточно иметь две ее проекции

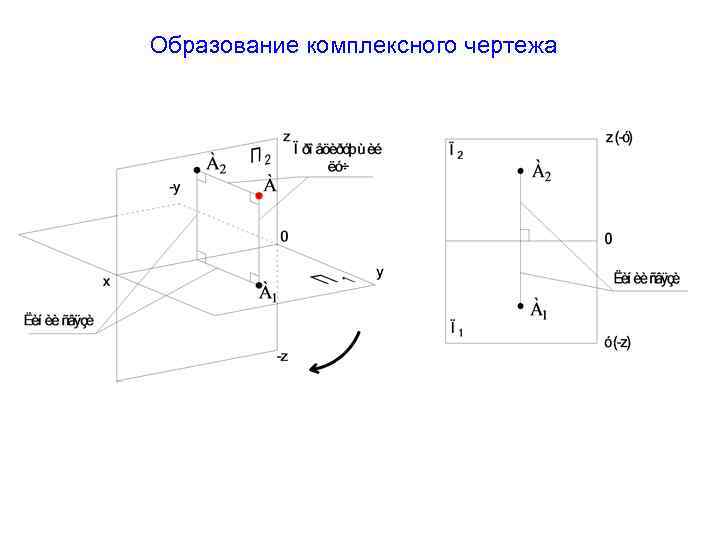Образование комплексного чертежа

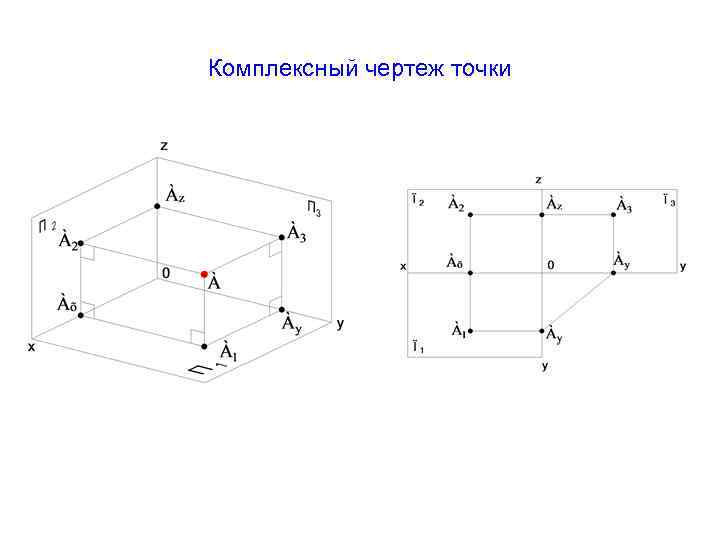Комплексный чертеж точки

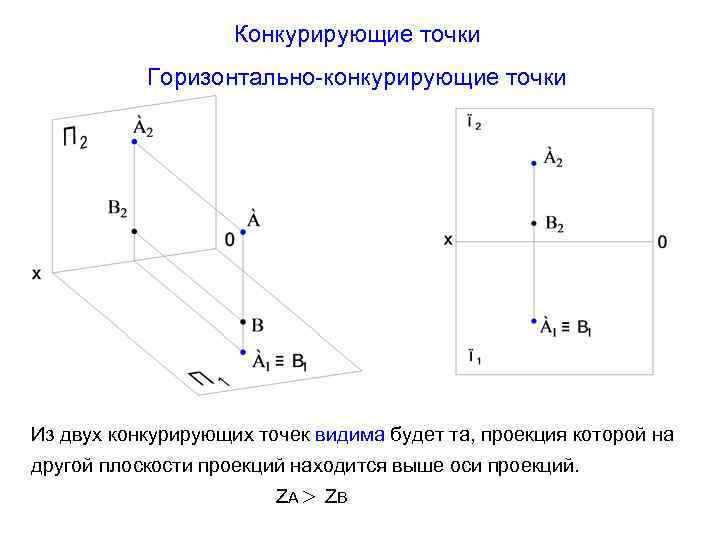Конкурирующие точки Горизонтально-конкурирующие точки Из двух конкурирующих точек видима будет та, проекция которой на другой плоскости проекций находится выше оси проекций. ZА ZВ

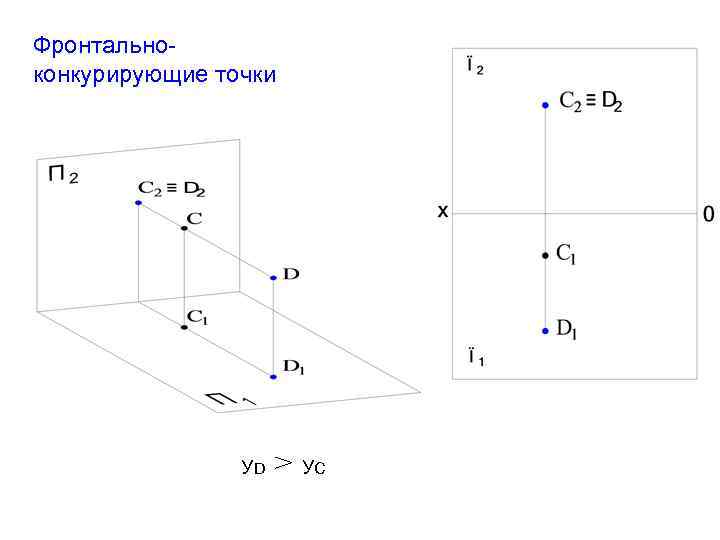Фронтальноконкурирующие точки УD УС

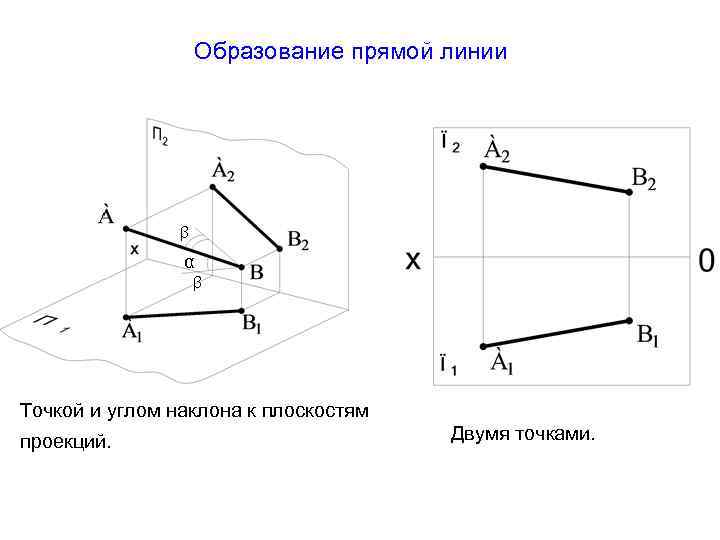Образование прямой линии β α β Точкой и углом наклона к плоскостям проекций. Двумя точками.

Образование прямой линии α β Двумя проекциями. Пересечением двух плоскостей.

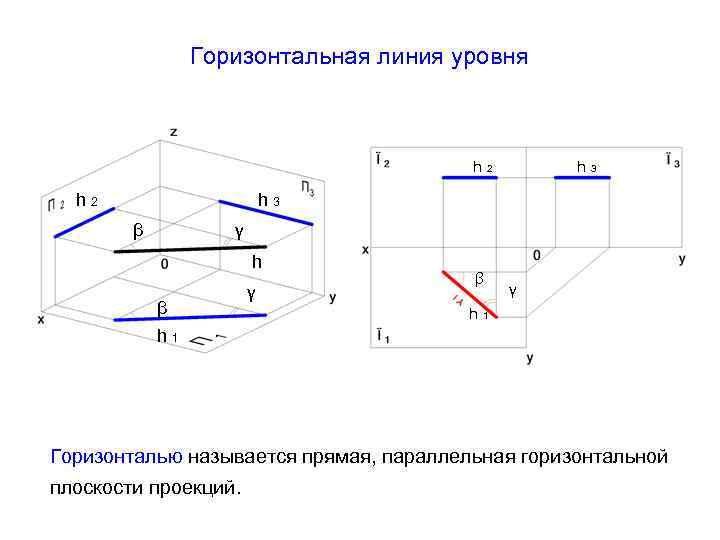Горизонтальная линия уровня h h 2 3 h 3 β γ h β γ β h γ 1 h 1 Горизонталью называется прямая, параллельная горизонтальной плоскости проекций.

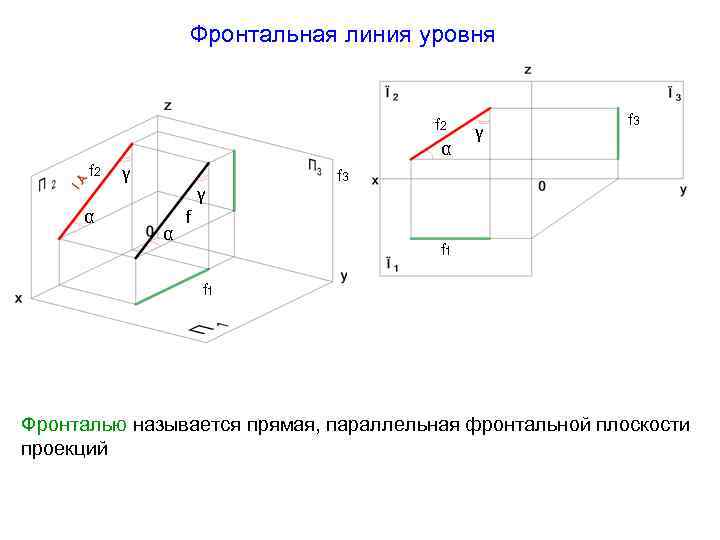Фронтальная линия уровня f 2 α f 2 γ γ α α γ f 3 f f 1 Фронталью называется прямая, параллельная фронтальной плоскости проекций

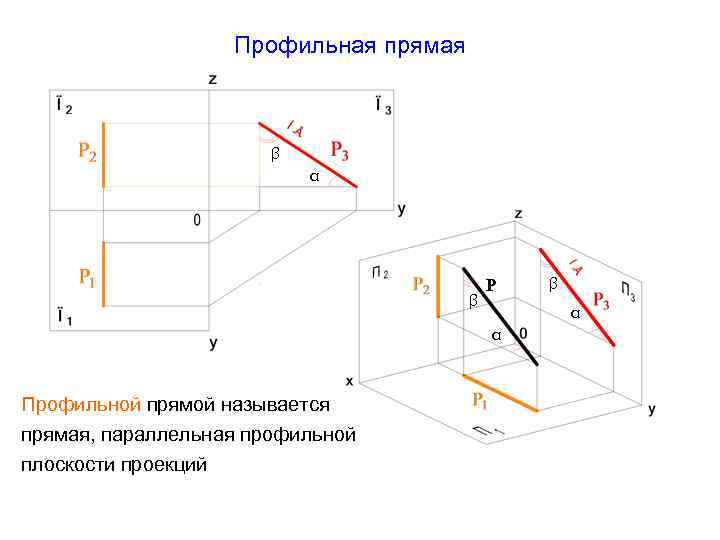Профильная прямая β α β P α α Профильной прямой называется прямая, параллельная профильной плоскости проекций β

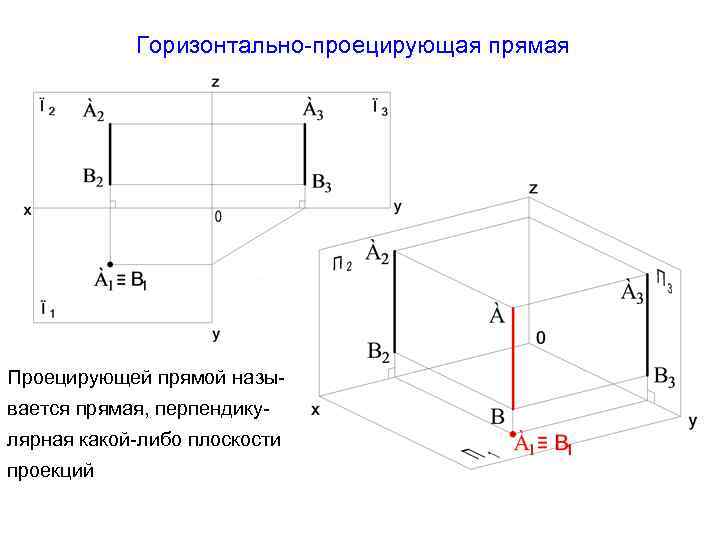Горизонтально-проецирующая прямая Проецирующей прямой называется прямая, перпендикулярная какой-либо плоскости проекций

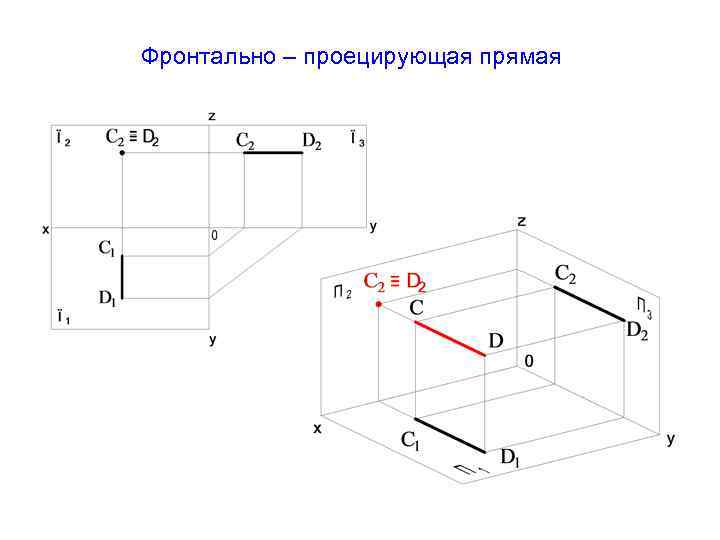Фронтально – проецирующая прямая

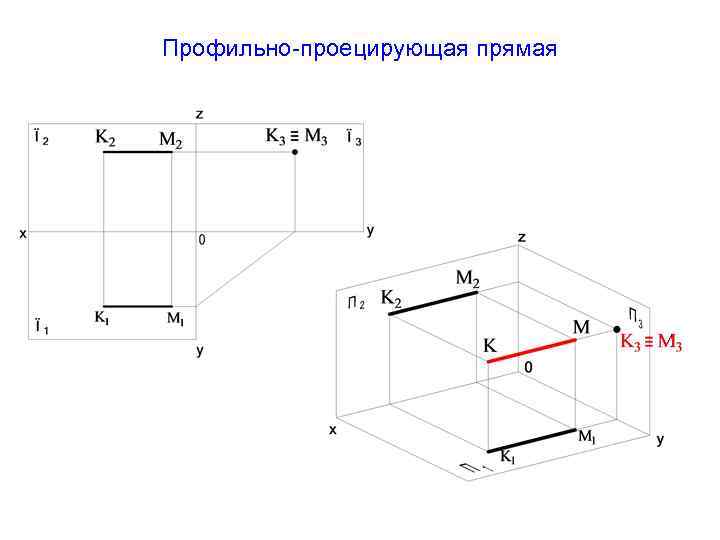Профильно-проецирующая прямая

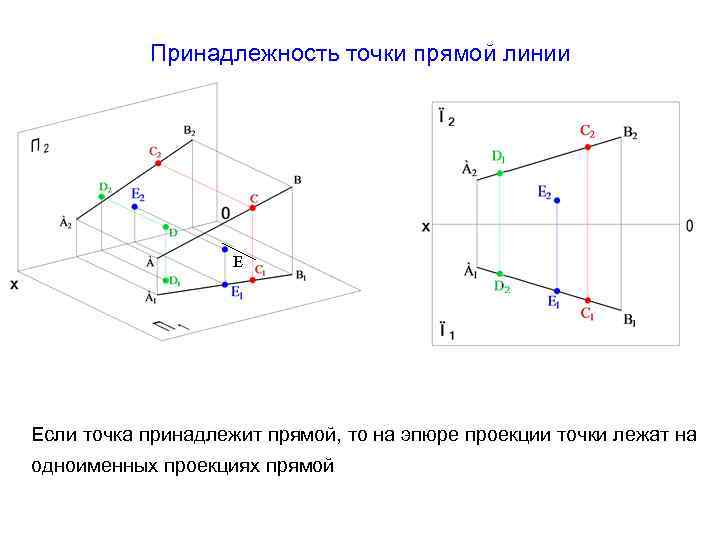Принадлежность точки прямой линии Е Если точка принадлежит прямой, то на эпюре проекции точки лежат на одноименных проекциях прямой