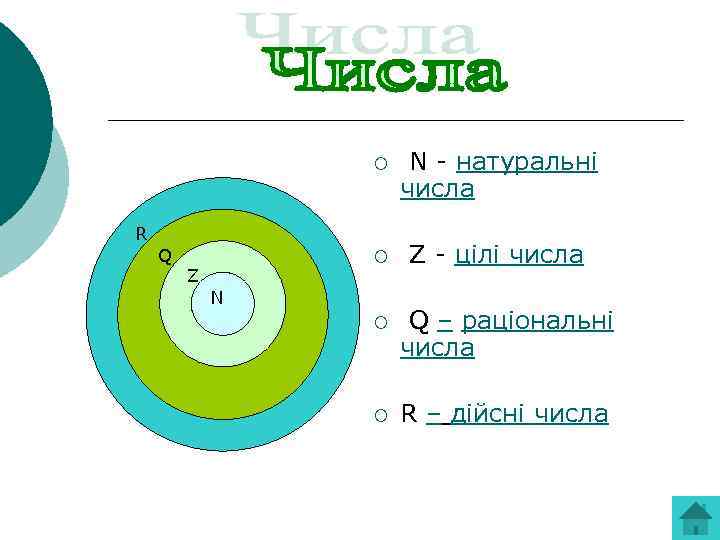
 ¡ N - натуральні числа R ¡ Z Z - цілі числа ¡ Q Q – раціональні числа N ¡ R – дійсні числа
¡ N - натуральні числа R ¡ Z Z - цілі числа ¡ Q Q – раціональні числа N ¡ R – дійсні числа
 N – натуральні числа ¡ Числа 1, 2, 3, …, що використовуються при лічбі, утворюють множину натуральних чисел. Позначають літерою N. Довільне натуральне число в десятковій системі числення записується за допомогою цифр 0, 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9. Наприклад, запис 2457 означає, що 2457=2 • 1000+4 • 100+5 • 10+7. ¡ Взагалі якщо а - цифра тисяч, b –цифра сотень, d- цифра десятків и c- цифра одиниць, то маємо а • 1000+b • 100+c • 10+d. Використовується також скорочений запис аbcd. ¡ 1 2 3 4 5
N – натуральні числа ¡ Числа 1, 2, 3, …, що використовуються при лічбі, утворюють множину натуральних чисел. Позначають літерою N. Довільне натуральне число в десятковій системі числення записується за допомогою цифр 0, 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9. Наприклад, запис 2457 означає, що 2457=2 • 1000+4 • 100+5 • 10+7. ¡ Взагалі якщо а - цифра тисяч, b –цифра сотень, d- цифра десятків и c- цифра одиниць, то маємо а • 1000+b • 100+c • 10+d. Використовується також скорочений запис аbcd. ¡ 1 2 3 4 5
 Цілі числа ¡ Натуральні числа, протилежні до них числа і число нуль складають множину цілих чисел. Позначають літерою Z. -5 -4 -3 -2 -1 0 1 2 3 4 5
Цілі числа ¡ Натуральні числа, протилежні до них числа і число нуль складають множину цілих чисел. Позначають літерою Z. -5 -4 -3 -2 -1 0 1 2 3 4 5
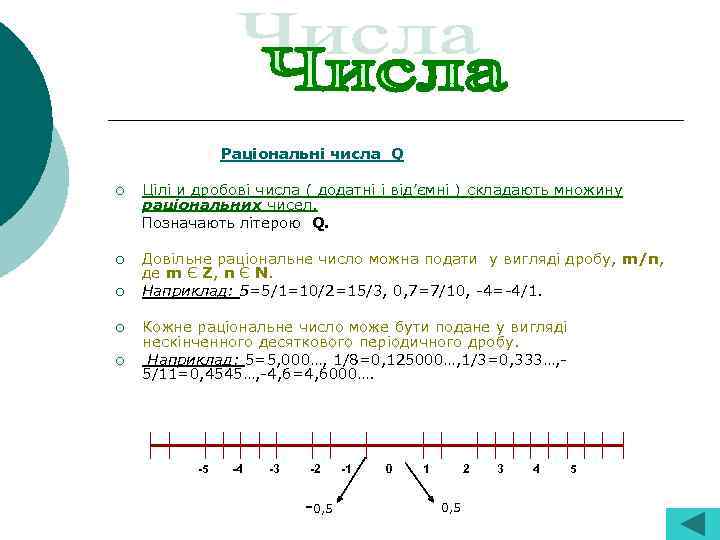 Раціональні числа Q Цілі и дробові числа ( додатні і від’ємні ) складають множину раціональних чисел. Позначають літерою Q. ¡ ¡ ¡ Довільне раціональне число можна подати у вигляді дробу, m/n, де m Є Z, n Є N. Наприклад: 5=5/1=10/2=15/3, 0, 7=7/10, -4=-4/1. Кожне раціональне число може бути подане у вигляді нескінченного десяткового періодичного дробу. Наприклад: 5=5, 000…, 1/8=0, 125000…, 1/3=0, 333…, 5/11=0, 4545…, -4, 6=4, 6000…. -5 -4 -3 -2 -0, 5 -1 0 1 2 0, 5 3 4 5
Раціональні числа Q Цілі и дробові числа ( додатні і від’ємні ) складають множину раціональних чисел. Позначають літерою Q. ¡ ¡ ¡ Довільне раціональне число можна подати у вигляді дробу, m/n, де m Є Z, n Є N. Наприклад: 5=5/1=10/2=15/3, 0, 7=7/10, -4=-4/1. Кожне раціональне число може бути подане у вигляді нескінченного десяткового періодичного дробу. Наприклад: 5=5, 000…, 1/8=0, 125000…, 1/3=0, 333…, 5/11=0, 4545…, -4, 6=4, 6000…. -5 -4 -3 -2 -0, 5 -1 0 1 2 0, 5 3 4 5
 Дійсні числа Множина дійсних чисел складається з раціональних та ірраціональних чисел. Позначають літерою R. ¡ Множину дійсних чисел називають також числовою прямою. Кажній точці координатної прямої відповідає деяке дійсне число, і кожному дійсному числу відповідає точка на координатній прямій. ¡ ¡ ¡ До ірраціональних числел відносяться нескінченні десяткові неперіодичні дроби. Наприклад: 3, 01001…, П ≈ 3, 145926…, √ 2 ≈1, 4. -√ 2 -5 -4 -3 √ 2 -2 -0, 5 -1 0 1 2 0, 5 3 4 5
Дійсні числа Множина дійсних чисел складається з раціональних та ірраціональних чисел. Позначають літерою R. ¡ Множину дійсних чисел називають також числовою прямою. Кажній точці координатної прямої відповідає деяке дійсне число, і кожному дійсному числу відповідає точка на координатній прямій. ¡ ¡ ¡ До ірраціональних числел відносяться нескінченні десяткові неперіодичні дроби. Наприклад: 3, 01001…, П ≈ 3, 145926…, √ 2 ≈1, 4. -√ 2 -5 -4 -3 √ 2 -2 -0, 5 -1 0 1 2 0, 5 3 4 5
 ¡ v v v v Які з тверджень правильні: Число 6 є цілим числом -4 є раціональним числом 6, 5 є раціональним 10, 1 є натуральним 13, (7) є раціональним -14, 101 є цілим 73 є натуральним і раціональним 3, 7(2) є цілим и раціональним
¡ v v v v Які з тверджень правильні: Число 6 є цілим числом -4 є раціональним числом 6, 5 є раціональним 10, 1 є натуральним 13, (7) є раціональним -14, 101 є цілим 73 є натуральним і раціональним 3, 7(2) є цілим и раціональним
 Розподіліть задані числа по вивченим множинам: ¡ 13, (2); -56; 8, 23; -3, 9; 34; 2, 10010001…. ;
Розподіліть задані числа по вивченим множинам: ¡ 13, (2); -56; 8, 23; -3, 9; 34; 2, 10010001…. ;
 Чи правильними є твердження: 1. 2. 3. 4. 5. 6. 7. Довільне ціле число є натуральним Довільне натуральне число є раціональним Число -7 є раціональним Сума двох натуральних чисел завжди є натуральне число Різниця двох натуральних чисел завжди є натуральне число Дійсне число не може бути натуральним Довільне ірраціональне число є дійсним
Чи правильними є твердження: 1. 2. 3. 4. 5. 6. 7. Довільне ціле число є натуральним Довільне натуральне число є раціональним Число -7 є раціональним Сума двох натуральних чисел завжди є натуральне число Різниця двох натуральних чисел завжди є натуральне число Дійсне число не може бути натуральним Довільне ірраціональне число є дійсним