n МОДЕЛИРОВАНИЕ n ХИМИКО- ТЕХНОЛОГИЧЕСКИХ n ПРОЦЕССОВ n

n. МОДЕЛИРОВАНИЕ n. ХИМИКО- ТЕХНОЛОГИЧЕСКИХ n. ПРОЦЕССОВ n. ПЕРЕРАБОТКИ n. ЭЛАСТОМЕРНЫХ n. МАТЕРИАЛОВ

МЫ ИЗУЧАЕМ МОДЕЛИ, А НЕ ГРЯЗНУЮ ДЕЙСТВИТЕЛЬНОСТЬ

n. Моделирование: создание модели, ее исследование и распространение полученных результатов на оригинал. n. Модель: некая система, которая ставится в соответствие оригиналу для его описания.

Закон и модель Y=a+b. X

Свойства диффузных систем n 1) нет непроницаемых перегородок между различными физико-химическими процессами, которыми сопровождается функционирование таких систем; n 2) высокая размерность задачи; n 3) связи между переменными не носят функционального характера; n 4) для описания диффузных систем используются методы многофакторного эксперимента.

Полимер как объект исследования n — Высокая молекулярная масса. n — Полидисперсность – смесь гомологов. n — Многокомпонентность, многофазность, гетерогенность, анизотропия. n — Неконтролируемые переменные. n — Низкая точность. n — Инерционность. n — Противоречивые требования.

Классификация моделей n 1. Математические (эскизные, программные, комбинированные, локально-интегральные). Их соотношение. n 2. Физические. n 3. Схематические. n Требования к процессу моделирования: экономичность, традуктивность. Критерии качества модели: адекватность, содержательность, предсказательная способность.

Способы моделирования n. Теория подобия. n. Теория соответственных состояний. n. Метод аналогий. n. Метод асимптотической коррекции.

Физико-химические основы моделирования n 1. Теплообмен. n. Виды теплообмена. n. Теплопроводность n. Конвекция n. Излучение

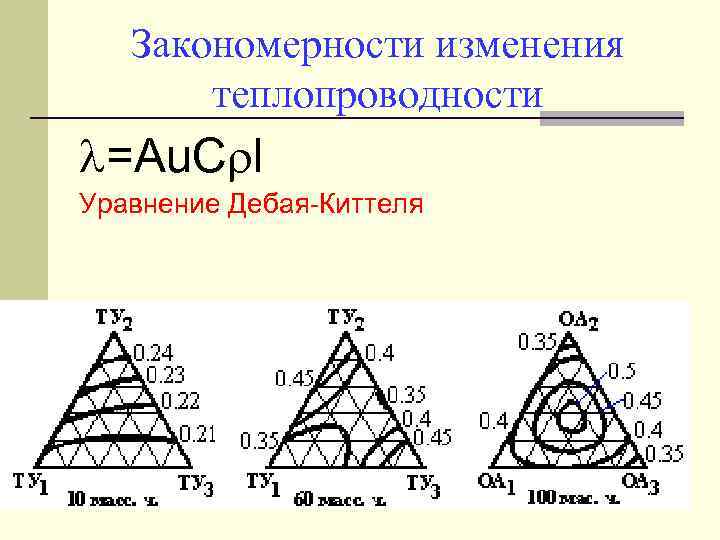Закономерности изменения теплопроводности =Au. C l Уравнение Дебая-Киттеля

2. Реология. n Предмет реологии. n Реология – наука о течении и деформации реальных сплошных сред. Она рассматривает процессы, связанные с необратимыми остаточными деформациями вещества, и является областью науки, находящейся между гидродинамикой и теорией упругости. Обычные уравнения гидродинамики вязкой жидкости неприменимы для реологических тел, т. к. эти тела обладают аномалией вязкости.

Уравнение Оствальда-Вейла n – индекс течения, 1/n =1 -5; K – коэффициент консистенции; K 0 – K при Т=Т 0; Е – энергия активации вязкого течения;

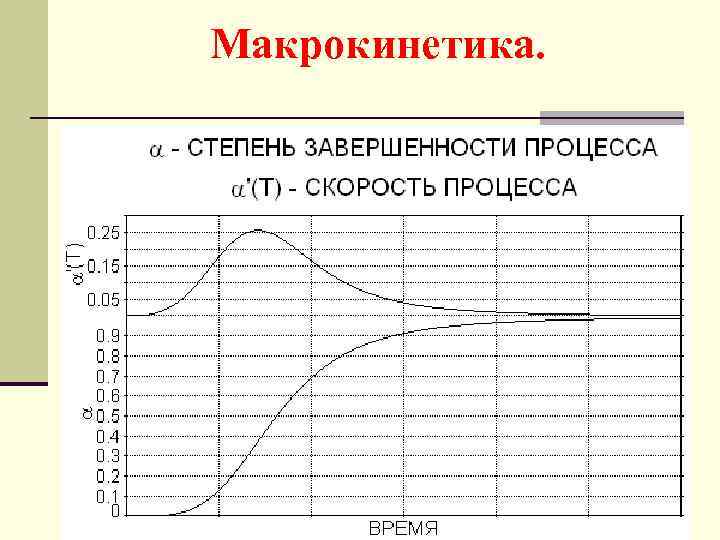Макрокинетика.

Планирование эксперимента. Область математической статистики, ставящая своей целью выбор количества и условий постановки экспериментов, необходимых и достаточных для решения задачи с требуемой точностью, разработку методов и приемов математической обработки результатов эксперимента и принятия на основе этого определенных решений.

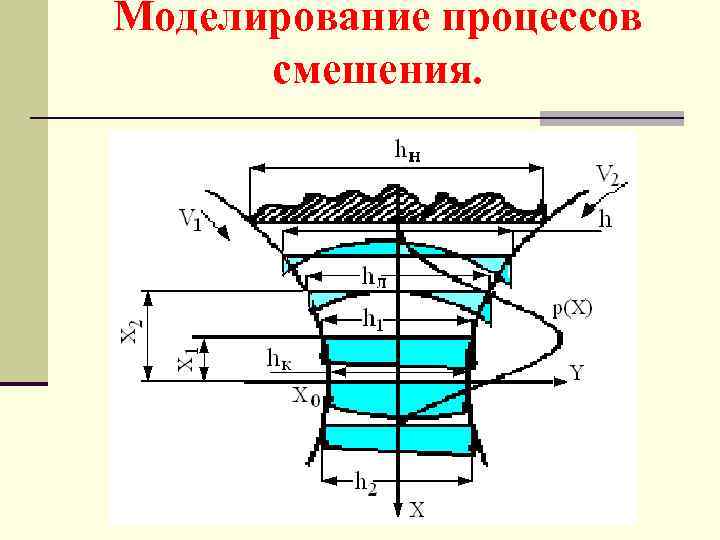Моделирование процессов смешения.

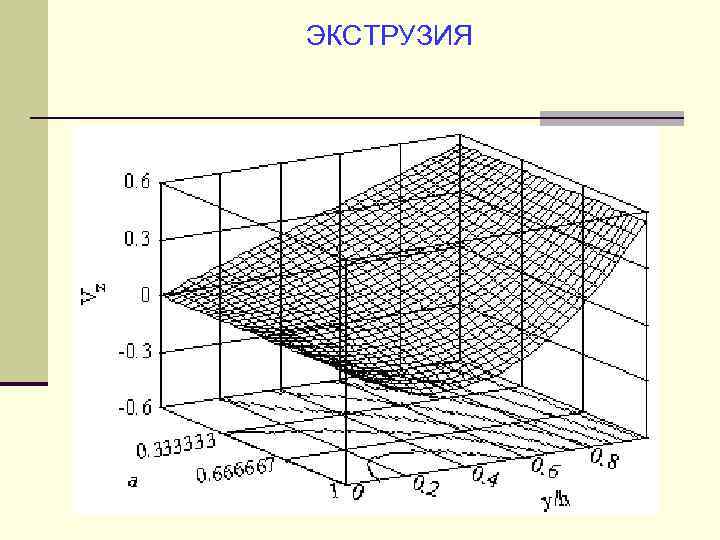ЭКСТРУЗИЯ

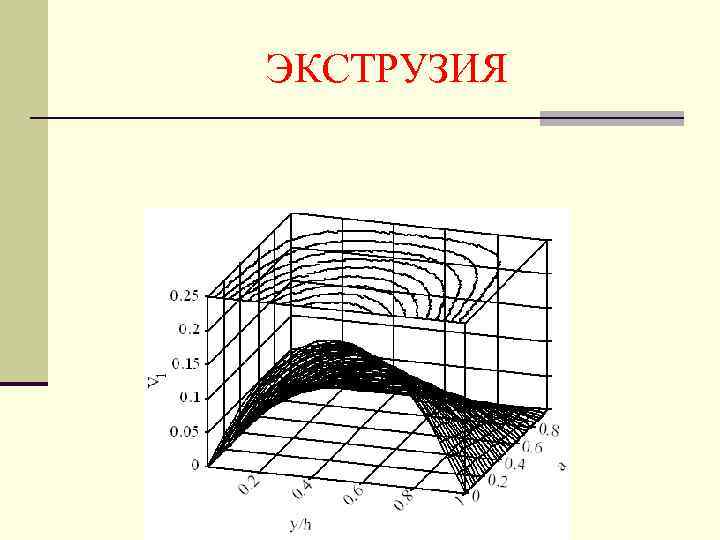ЭКСТРУЗИЯ

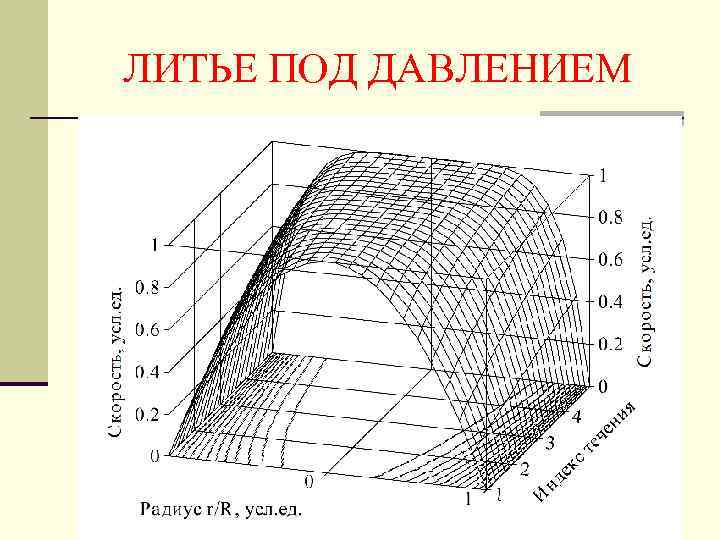ЛИТЬЕ ПОД ДАВЛЕНИЕМ

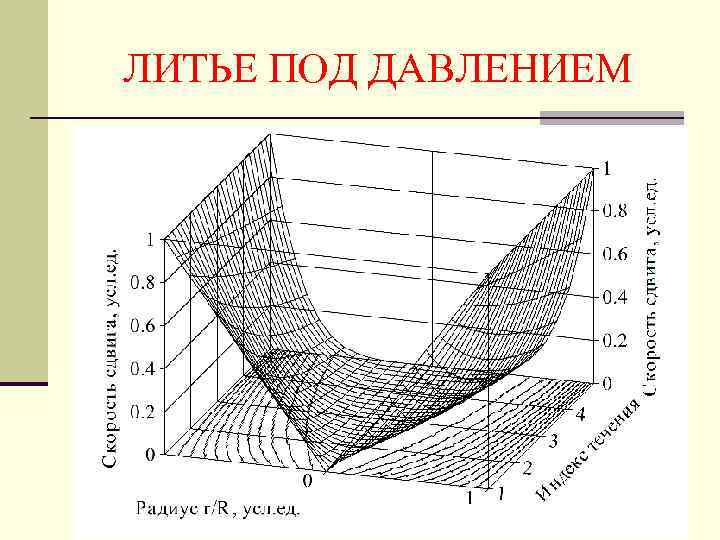ЛИТЬЕ ПОД ДАВЛЕНИЕМ

ВУЛКАНИЗАЦИЯ n Правило Вант-Гоффа K=k. T+5/k. T-5 n Уравнение Аррениуса Если считать, что k не зависит от T

Метод приращения эквивалентных времен Интенсивность процесса Эффективность (эффект) процесса Эквивалентное время

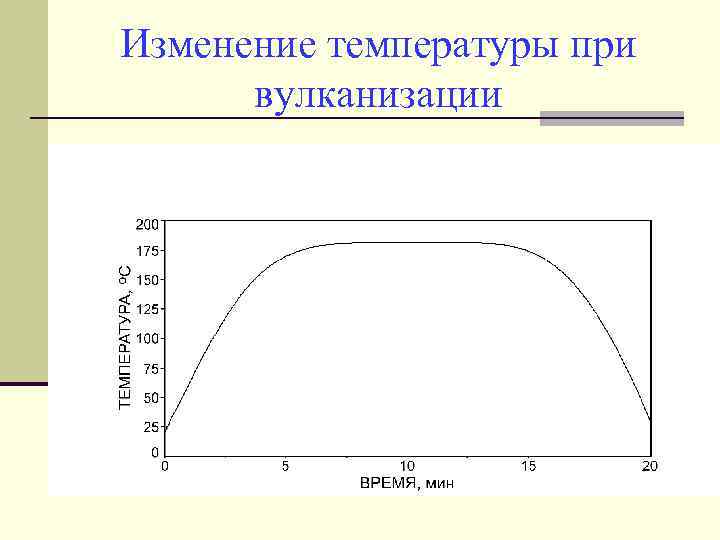Изменение температуры при вулканизации

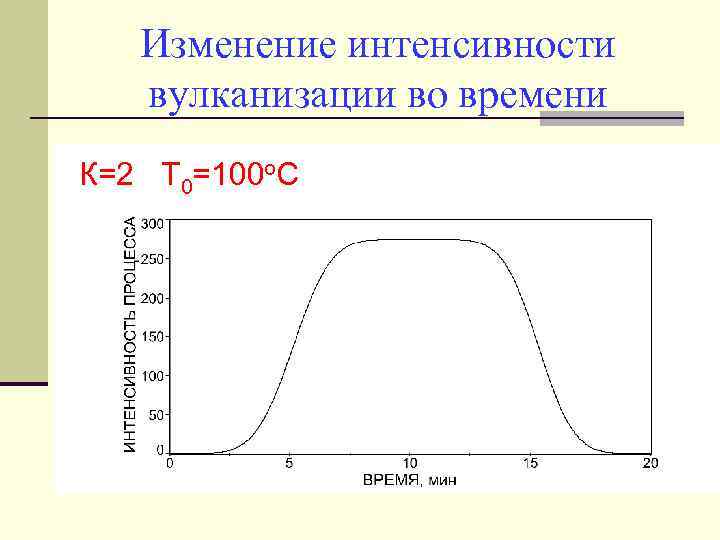Изменение интенсивности вулканизации во времени К=2 Т 0=100 о. С

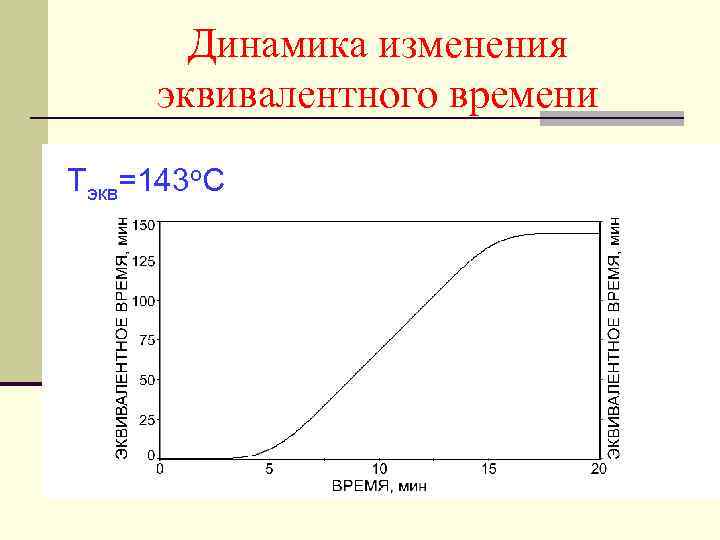Динамика изменения эквивалентного времени Тэкв=143 о. С

n. СПАСИБО!