Н









 Н А a Н А Расстояние от точки до прямой – длина плоскости – длина перпендикуляра, перпендикуляра опущенного из точки А на прямую.
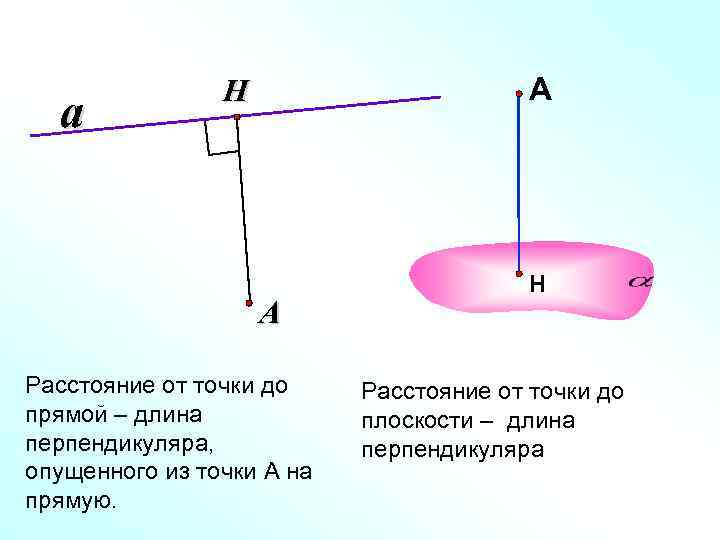
Н А a Н А Расстояние от точки до прямой – длина плоскости – длина перпендикуляра, перпендикуляра опущенного из точки А на прямую.
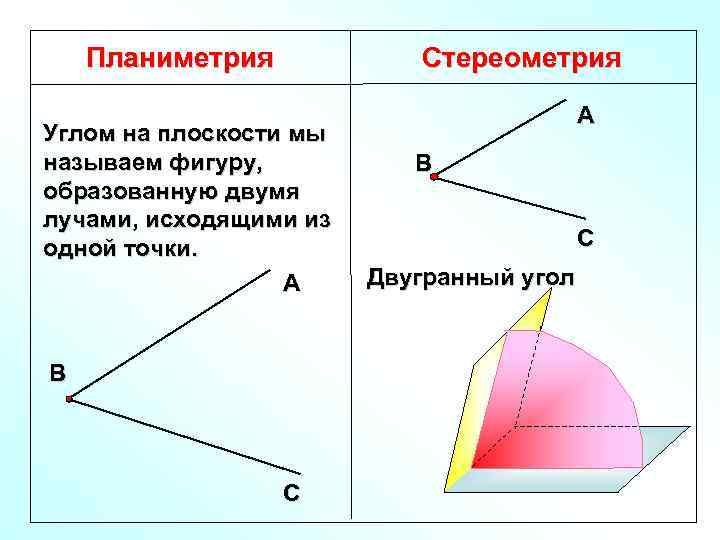
 Планиметрия Стереометрия А Углом на плоскости мы называем фигуру, В образованную двумя лучами, исходящими из одной точки. С А Двугранный угол В С
Планиметрия Стереометрия А Углом на плоскости мы называем фигуру, В образованную двумя лучами, исходящими из одной точки. С А Двугранный угол В С
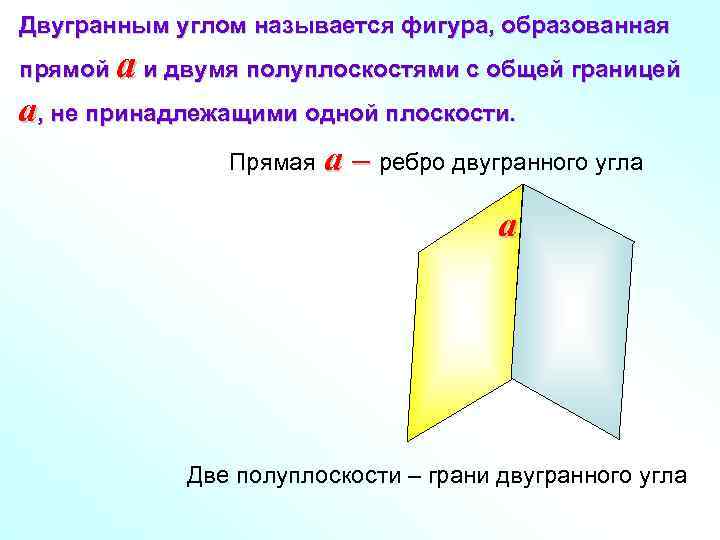
 Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Прямая a – ребро двугранного угла a Две полуплоскости – грани двугранного угла
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Прямая a – ребро двугранного угла a Две полуплоскости – грани двугранного угла
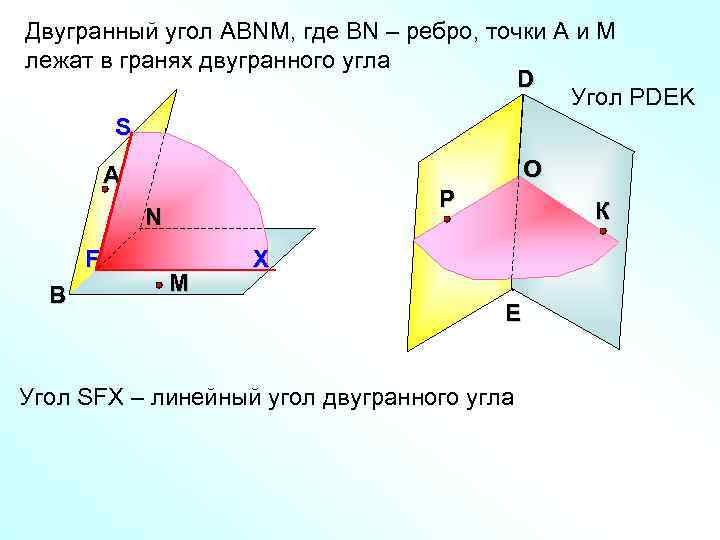
 Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в гранях двугранного угла D Угол РDEK S А O Р N К F X M В E Угол SFX – линейный угол двугранного угла
Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в гранях двугранного угла D Угол РDEK S А O Р N К F X M В E Угол SFX – линейный угол двугранного угла
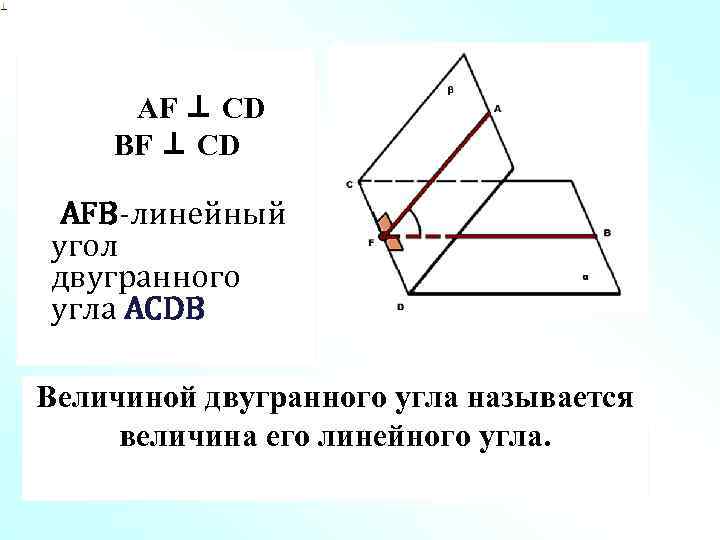
 AF ⊥ CD BF ⊥ CD AFB-линейный угол двугранного угла ACDВ Величиной двугранного угла называется величина его линейного угла.
AF ⊥ CD BF ⊥ CD AFB-линейный угол двугранного угла ACDВ Величиной двугранного угла называется величина его линейного угла.
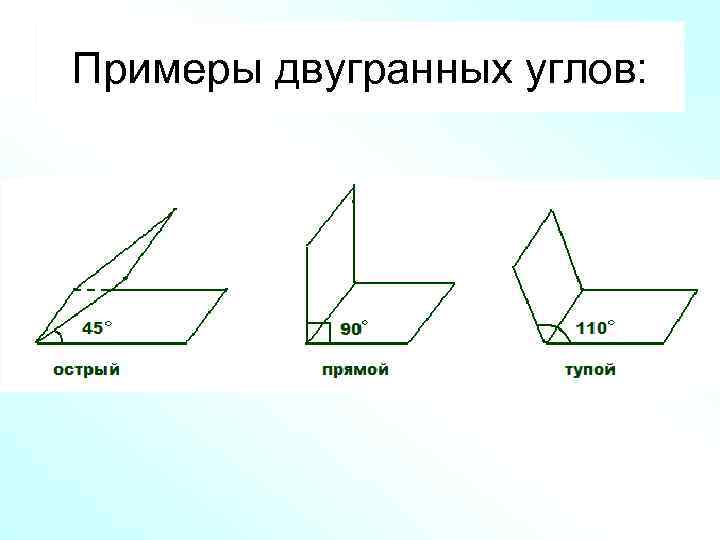
 Примеры двугранных углов:
Примеры двугранных углов:
 Определение: Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.
Определение: Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.
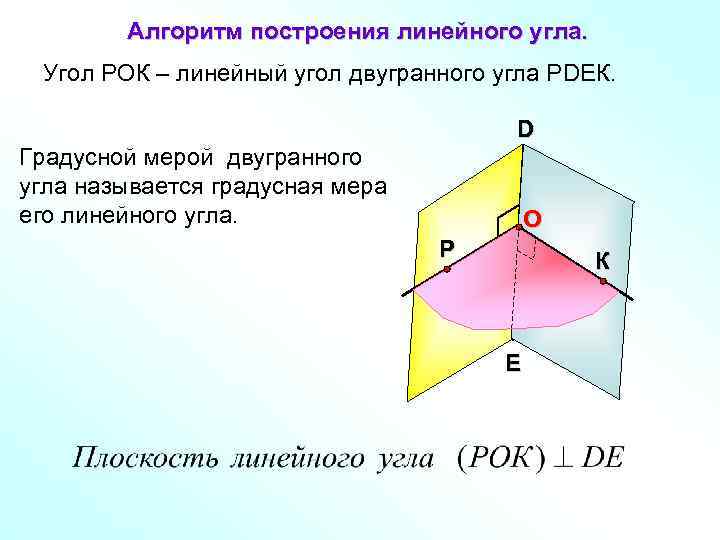
 Алгоритм построения линейного угла. Угол РОК – линейный угол двугранного угла РDEК. D Градусной мерой двугранного угла называется градусная мера его линейного угла. O Р К E
Алгоритм построения линейного угла. Угол РОК – линейный угол двугранного угла РDEК. D Градусной мерой двугранного угла называется градусная мера его линейного угла. O Р К E
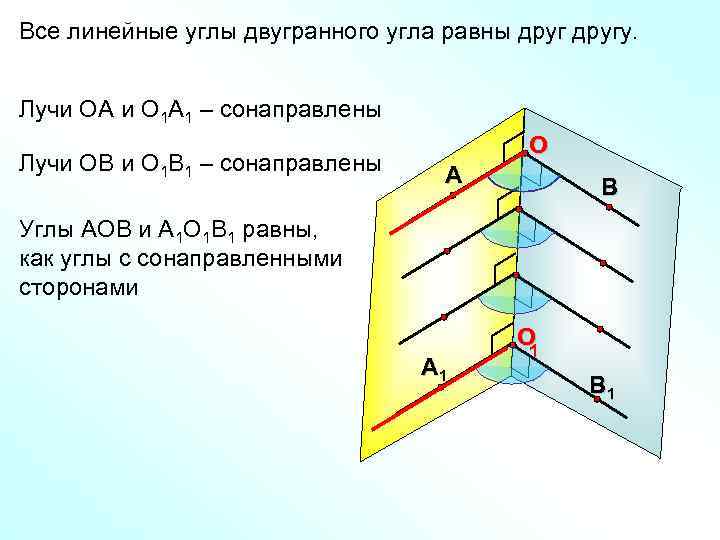
 Все линейные углы двугранного угла равны другу. Лучи ОА и О 1 А 1 – сонаправлены O Лучи ОВ и О 1 В 1 – сонаправлены А В Углы АОВ и А 1 О 1 В 1 равны, как углы с сонаправленными сторонами O 1 А 1 В 1
Все линейные углы двугранного угла равны другу. Лучи ОА и О 1 А 1 – сонаправлены O Лучи ОВ и О 1 В 1 – сонаправлены А В Углы АОВ и А 1 О 1 В 1 равны, как углы с сонаправленными сторонами O 1 А 1 В 1
 Построить линейный угол двугранного угла ВАСК. Треугольник АВС – равнобедренный. TTП АС ВМ АС NМ В H-я П-р Н-- Н яя А К П-я M N С Угол ВMN – линейный угол двугранного угла ВАСК
Построить линейный угол двугранного угла ВАСК. Треугольник АВС – равнобедренный. TTП АС ВМ АС NМ В H-я П-р Н-- Н яя А К П-я M N С Угол ВMN – линейный угол двугранного угла ВАСК
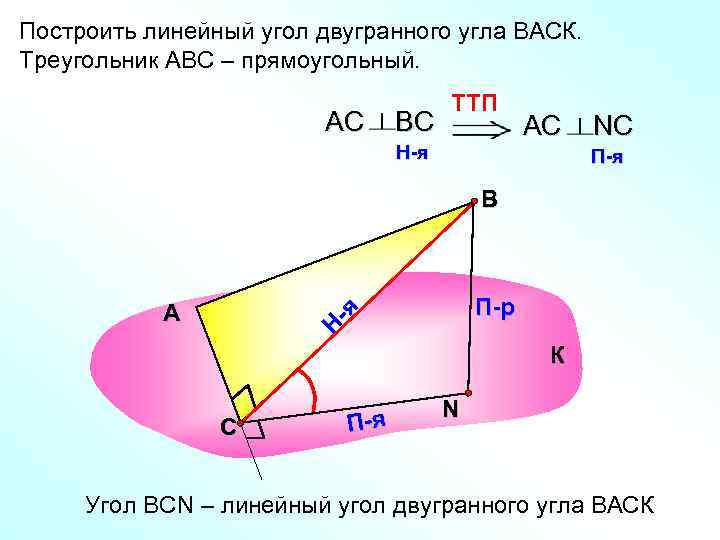
 Построить линейный угол двугранного угла ВАСК. Треугольник АВС – прямоугольный. TTП АС ВС АС NС H-я П-я В А П-р -я Н К N С П-я Угол ВСN – линейный угол двугранного угла ВАСК
Построить линейный угол двугранного угла ВАСК. Треугольник АВС – прямоугольный. TTП АС ВС АС NС H-я П-я В А П-р -я Н К N С П-я Угол ВСN – линейный угол двугранного угла ВАСК
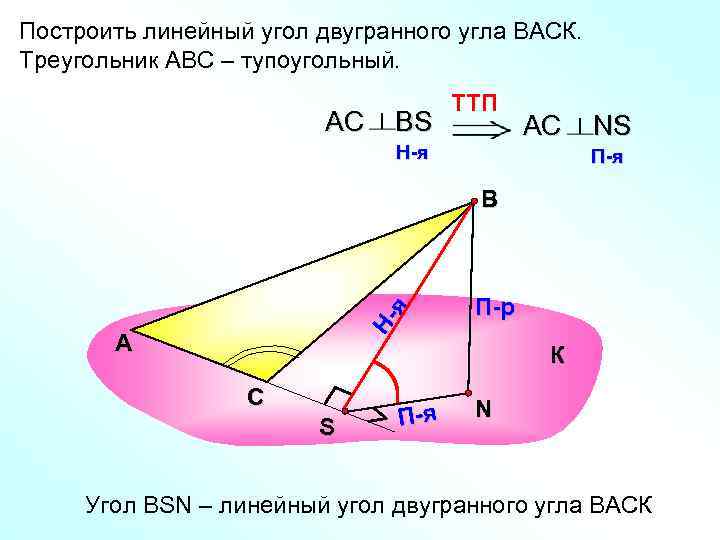
 Построить линейный угол двугранного угла ВАСК. Треугольник АВС – тупоугольный. TTП АС ВS АС NS H-я П-я В П-р я Н- А К С П-я N S Угол ВSN – линейный угол двугранного угла ВАСК
Построить линейный угол двугранного угла ВАСК. Треугольник АВС – тупоугольный. TTП АС ВS АС NS H-я П-я В П-р я Н- А К С П-я N S Угол ВSN – линейный угол двугранного угла ВАСК
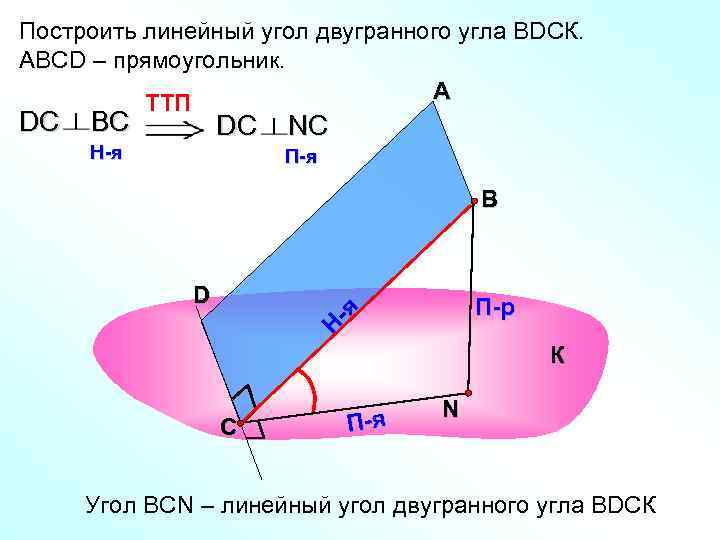
 Построить линейный угол двугранного угла ВDСК. АВСD – прямоугольник. TTП А DС BС DС NС H-я П-я В D П-р -я Н К N С П-я Угол ВСN – линейный угол двугранного угла ВDСК
Построить линейный угол двугранного угла ВDСК. АВСD – прямоугольник. TTП А DС BС DС NС H-я П-я В D П-р -я Н К N С П-я Угол ВСN – линейный угол двугранного угла ВDСК
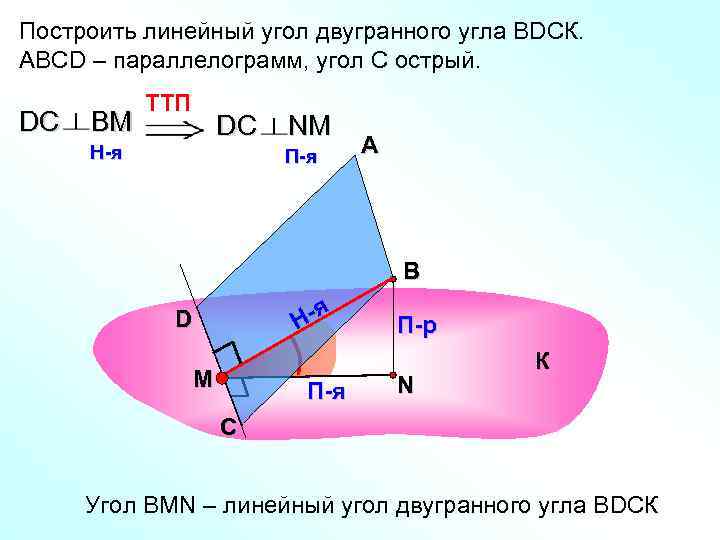
 Построить линейный угол двугранного угла ВDСК. АВСD – параллелограмм, угол С острый. TTП DС ВM DС NM H-я П-я А В я D Н- П-р К M N П-я С Угол ВMN – линейный угол двугранного угла ВDСК
Построить линейный угол двугранного угла ВDСК. АВСD – параллелограмм, угол С острый. TTП DС ВM DС NM H-я П-я А В я D Н- П-р К M N П-я С Угол ВMN – линейный угол двугранного угла ВDСК
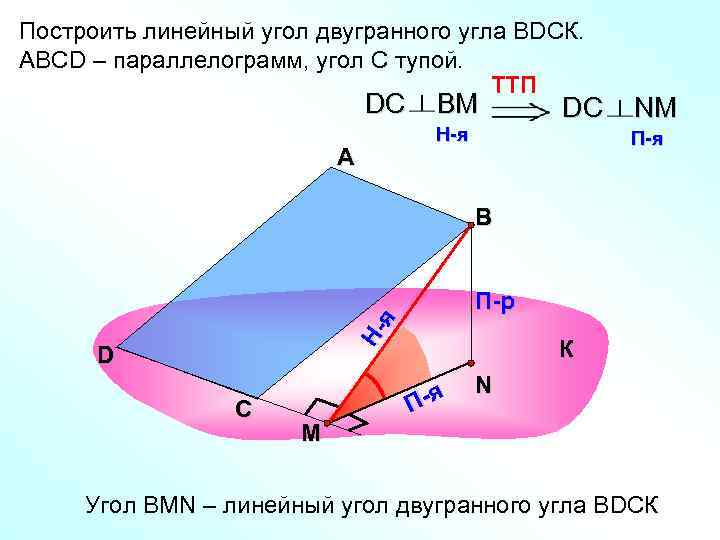
 Построить линейный угол двугранного угла ВDСК. АВСD – параллелограмм, угол С тупой. TTП DС ВM DС NM H-я П-я А В П-р я Н- D К N С П-я M Угол ВMN – линейный угол двугранного угла ВDСК
Построить линейный угол двугранного угла ВDСК. АВСD – параллелограмм, угол С тупой. TTП DС ВM DС NM H-я П-я А В П-р я Н- D К N С П-я M Угол ВMN – линейный угол двугранного угла ВDСК
 Построить линейный угол двугранного угла ВDСК. АВСD – трапеция, угол С острый. TTП DС ВM DС NM H-я П-я А В П-р я Н- D К N П-я M С Угол ВMN – линейный угол двугранного угла ВDСК
Построить линейный угол двугранного угла ВDСК. АВСD – трапеция, угол С острый. TTП DС ВM DС NM H-я П-я А В П-р я Н- D К N П-я M С Угол ВMN – линейный угол двугранного угла ВDСК
 Задача 1: В кубе A…D 1 найдите угол между плоскостями BC 1 D и BA 1 D. Решение: Пусть О – середина ВD. A 1 OC 1 – линейный угол двугранного угла А 1 ВDС 1.
Задача 1: В кубе A…D 1 найдите угол между плоскостями BC 1 D и BA 1 D. Решение: Пусть О – середина ВD. A 1 OC 1 – линейный угол двугранного угла А 1 ВDС 1.
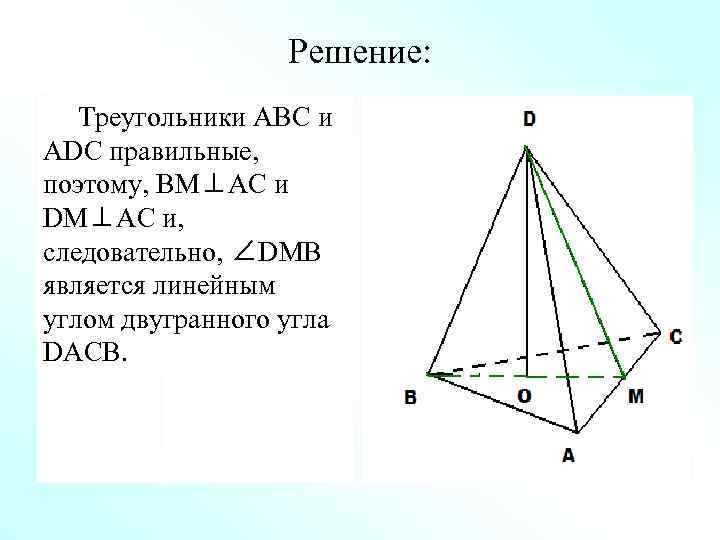
 Задача 2: В тетраэдре DABC все ребра равны, точка М – середина ребра АС. Докажите, что ∠DMB – линейный угол двугранного угла BACD.
Задача 2: В тетраэдре DABC все ребра равны, точка М – середина ребра АС. Докажите, что ∠DMB – линейный угол двугранного угла BACD.
 Решение: Треугольники ABC и ADC правильные, поэтому, BM⊥AC и DM⊥AC и, следовательно, ∠DMB является линейным углом двугранного угла DACB.
Решение: Треугольники ABC и ADC правильные, поэтому, BM⊥AC и DM⊥AC и, следовательно, ∠DMB является линейным углом двугранного угла DACB.
 Задача 3: Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр ВВ 1. Найдите расстояние от точки В до прямой АС и до плоскости α, если АВ=2, ∠ВАС=1500 и двугранный угол ВАСВ 1 равен 450.
Задача 3: Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр ВВ 1. Найдите расстояние от точки В до прямой АС и до плоскости α, если АВ=2, ∠ВАС=1500 и двугранный угол ВАСВ 1 равен 450.
 Решение: 1) АВС – тупоугольный треугольник с тупым углом А, поэтому основание высоты ВК лежит на продолжении стороны АС. ВК – расстояние от точки В до АС. ВВ 1 – расстояние от точки В до плоскости α
Решение: 1) АВС – тупоугольный треугольник с тупым углом А, поэтому основание высоты ВК лежит на продолжении стороны АС. ВК – расстояние от точки В до АС. ВВ 1 – расстояние от точки В до плоскости α
 2) Так как АС⊥ВК, то АС⊥КВ 1 (по теореме , обратной теореме о трех перпендикулярах). Следовательно, ∠ВКВ 1 – линейный угол двугранного угла ВАСВ 1 и ∠ВКВ 1=450. 3) ∆ВАК: ∠А=300, ВК=ВА·sin 300, ВК =1. ∆ВКВ 1: ВВ 1=ВК·sin 450, ВВ 1=
2) Так как АС⊥ВК, то АС⊥КВ 1 (по теореме , обратной теореме о трех перпендикулярах). Следовательно, ∠ВКВ 1 – линейный угол двугранного угла ВАСВ 1 и ∠ВКВ 1=450. 3) ∆ВАК: ∠А=300, ВК=ВА·sin 300, ВК =1. ∆ВКВ 1: ВВ 1=ВК·sin 450, ВВ 1=

