Мы хорошо знаем что при решении квадратных уравнений

Мы хорошо знаем, что при решении квадратных уравнений большую роль играет дискриминант. Но очень часто мы сталкиваемся не только с задачей о количестве корней, но и с задачей о расположении этих корней на числовой прямой. Например: Сколько корней в зависимости от значений параметра a имеет уравнение 4 sin 2 x-sinx-3=a. Сделав замену sin x = t, где |t|≤ 1, мы получаем уравнение 4 t 2 -t-3 -a=0. Таким образом наша задача свелась к определению количества корней квадратного уравнения относительно отрезка [-1; 1]. Поэтому рассмотрим более подробно вопрос о нахождении корней квадратного уравнения ax 2+bx+c=0 в следующих случаях: а) оба корня (x 1 и x 2) меньше заданного числа М. б) оба корня (x 1 и x 2) больше заданного числа М. в) x 1M г) один корень принадлежит отрезку (M; N). д) оба корня принадлежат отрезку (M; N). е) и случай, когда ни один из корней не принадлежит отрезку (M; N). Для удобства рассуждений я рассматривала все эти вопросы при помощи графика квадратного трёхчлена, т. е. параболы y=ax 2+bx+c.

Рассмотрим некоторые задачи, связанные с расположением корней квадратного трёхчлена y=ax 2+bx+c относительно точек M и N таких, что M

1. Оба корня меньше заданного числа M, т. е. x 10 если a<0 XВ M f (M) X 1 X X 2 f (M) M XВ a>0 f (M)>0 a*f (M)>0 a<0 f (M)<0 a*f (M)>0

Найдём условия, объединяющие оба графика : D ≥ 0 xв0 * a) Уравнение имеет два различных корня, следовательно D>0 б) Корни уравнения меньше М, следовательно D≥ 0

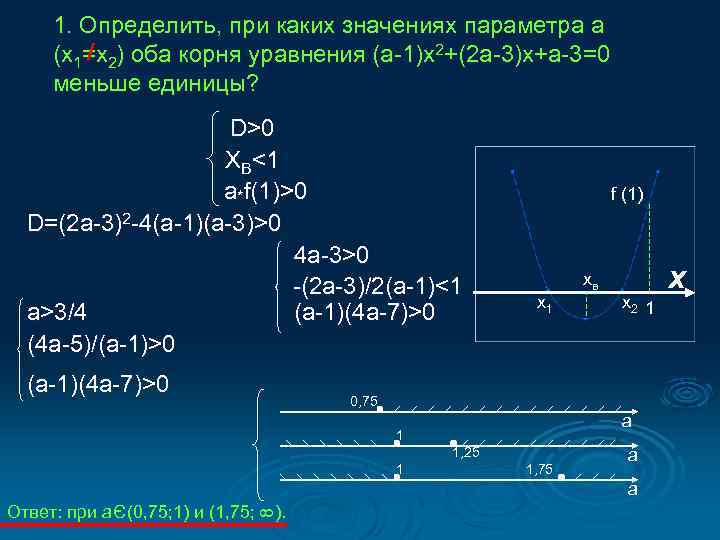1. Определить, при каких значениях параметра a (x 1=x 2) оба корня уравнения (а-1)x 2+(2 a-3)x+a-3=0 меньше единицы? D>0 XВ<1 a*f(1)>0 D=(2 a-3)2 -4(a-1)(a-3)>0 4 a-3>0 -(2 a-3)/2(a-1)<1 a>3/4 (a-1)(4 a-7)>0 (4 a-5)/(a-1)>0 (a-1)(4 a-7)>0 f (1) x 1 xв x 2 1 0, 75 a 1 1, 25 1 1, 75 a a ). 8 Э Ответ: при a (0, 75; 1) и (1, 75; x

2. Один корень меньше, другой больше заданного числа М, т. е. X 1M если a>0 если a<0 f (M) X 1 a>0 f (M)<0 f (M) X X M X 1 M X 2 a*f (M)<0 a<0 f (M)>0 a*f (M)<0

Найдём условия, объединяющие оба графика : a* f (M)<0 * Т. к. существует точка x=M, в которой f (M)<0, то парабола f =ax 2+bx+c обязательно будет иметь два различных корня. Следовательно, требование D>0 НЕОБЯЗАТЕЛЬНО!

2. Определить, при каких значениях параметра k 1 (x 2; x 1) для уравнения (k-1)x 2+(k+4)x+k+7=0 ? Э a*f (1)<0 (k-1)(3 k+10)<0 X 1 x 2 x 1 f (1) -10/3 1 k Э Ответ: при k (-10/3; 1).

3. Оба корня больше заданного числа M, т. е. X 1>M X 2>M если a>0 если a<0 Xв M f (M) X 1 X 2 X M X X 2 f (M) Xв a>0 f (M)>0 a*f (M)>0 a<0 f (M)<0 a*f (M)>0

Найдём условия, объединяющие оба графика : D≥ 0 x В0 * а) Уравнение имеет два различных корня, следовательно D≥ 0 б) Корни уравнения больше М, следовательно D>0

3. Определить, при каких значениях параметра a оба корня уравнения (a+2)x 2+3 ax-2 a=0 больше 0, 5? D>0 XВ>0, 5 a *f (0, 5)>0 f (0, 5) D=(3 a)2+8(a+2)a=a(17 a+16)>0 -3 a/2(a+2)>1/2 (a+2)((a+2)/4+3 a/2 -2 a)>0 a(17 a+16)>0 (2 a+1)/(a+2)<0 -16/17 (a+2)(2 -a)/4>0. -2 -2 Э Ответ: при a (-2; -16/17). 0, 5 x 2 x. В 0 a -1/2 2 a a X x 1

4. Оба корня принадлежат промежутку (M; N) если a>0 f (M) если a<0 M f (N) X 1 M X 1 X X 2 N Xв f (M) N X X 2 f (N) Xв a>0 f (M)>0 a>0 f (N)>0 a*f (M)>0 a<0 f (M)<0 a*f (M)>0 a*f (N)>0 a<0 f (N)<0 a*f (N)>0

Найдём условия, объединяющие оба графика : D>0 M0 a *f (N)>0

4. Определить, при каких значениях параметра b (x 2; x 1) принадлежат промежутку (-1; 1), где x 2 и x 1 – корни уравнения (b-2)x 2+(b+3)x+b+6=0 ? D>0 -10 f (-1) D=(b+3)2 -4(b-2)(b+6)=-(b-3)(3 b+19)>0 -1<-(b+3)/2(b-2)<1 (-b-3)(3 b+19)>0 (b-2)(b-2 -b-3+b+6)>0 (-3 b -1)/(b-2)>0 (b-2)(b-2+b+3+b+6)>0 (7 -b)/2(b-2)<0 -19/3 (b-2)(3 b+7)>0 1/3 (b-2)(b+1)>0. -7/3 Э Ответ: при b (-19/3; -7/3). -1 f (1) x. В -1 x 2 x 1 1 3 2 2 7 a a a X

5. Меньший корень принадлежит промежутку (M; N) , а больший нет, т. е. X 1 (M; N) X 2 (M; N) X 10 если a<0 M X 1 f (M) M X 1 a>0 f (M)>0 X X 2 f (N) a*f (M)>0 X N a>0 f (N)<0 N f (N) X 2 a*f (N)<0 a<0 f (N)>0 a*f (N)<0 f (M) a<0 f (M)<0 a*f (M)>0

Найдём условия, объединяющие оба графика : a *f (M)>0 a *f (N)<0

5. Определить, при каких значениях параметра k x 1>x 2 (1; 2) где x 1 и x 2 – корни уравнения x 1 (1; 2), (k-2)x 2+(k+2)x+k-5=0 Э Э a *f (2)<0 a *f (1)>0 f (1) (k-2)(k-2+k+2+k-5)>0 (k-2)(4 k-8+2 k+4+k-5)<0 2 1 (k-2)(3 k-5)>0 (k-2)(7 k-9)<0 x 1 f (2) 5/3 9/7 2 2 k k Э Ответ: при k x 2 (9/7; 5/3). X

6. Больший корень принадлежит промежутку (M; N), а меньший нет, т. е. X 1 (M; N) X 2 (M; N) X 10 f (N)>0 X M X 1 X 2 N f (M) если a>0 f (M)<0 a*f (M)<0 a<0 f (N)<0 a*f (N)>0 X 1 M X X 2 f (N) a*f (N)>0 если a<0 f (M)>0 a*f (M)<0

Найдём условия, объединяющие оба графика: f (M)*f (N)<0 a*f (M)<0 a*f (N)>0

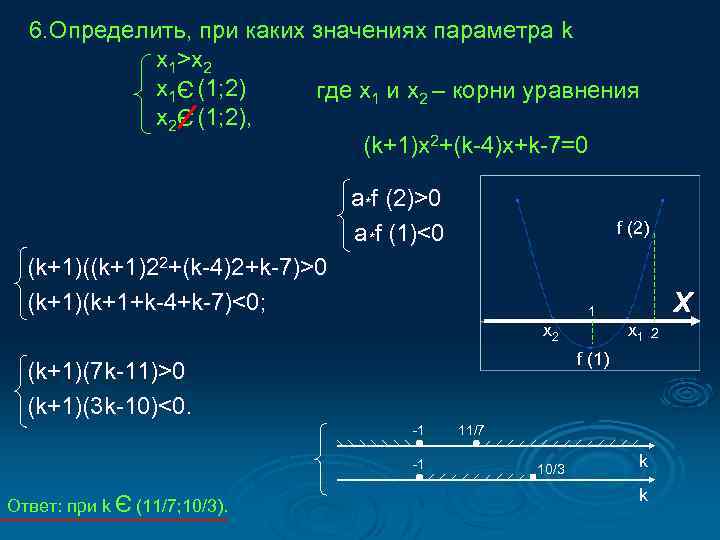6. Определить, при каких значениях параметра k x 1>x 2 x 1 (1; 2) где x 1 и x 2 – корни уравнения x 2 (1; 2), (k+1)x 2+(k-4)x+k-7=0 Э Э a *f (2)>0 a *f (1)<0 f (2) (k+1)((k+1)22+(k-4)2+k-7)>0 (k+1)(k+1+k-4+k-7)<0; x 2 -1 -1 (11/7; 10/3). x 1 f (1) (k+1)(7 k-11)>0 (k+1)(3 k-10)<0. Э Ответ: при k X 1 11/7 10/3 k k 2

7. Заданные точки M и N принадлежат промежутку (X 1; X 2), т. е. X 10 если a>0 f (M)<0 a*f (M)<0 a>0 f (N)<0 a*f (N)<0 a<0 если f (M)>0 a<0 f (N)>0 a<0 a*f (M)<0 a*f (N)<0

Найдём условия, объединяющие оба графика: a*f (M)<0 a *f (N)<0

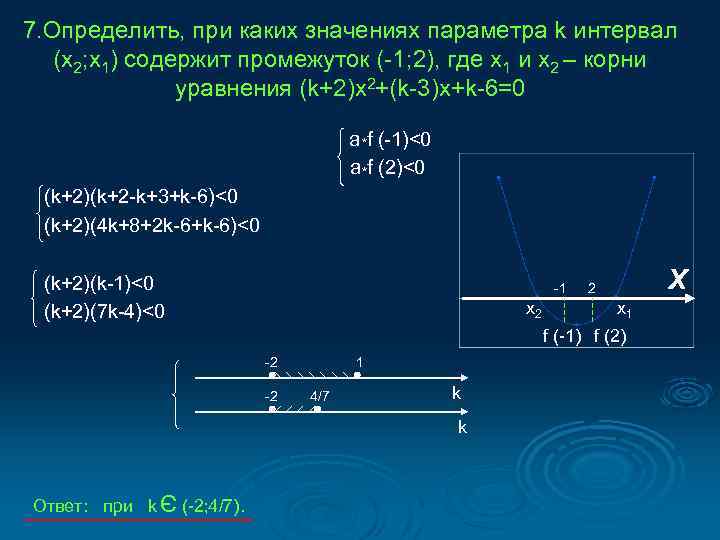7. Определить, при каких значениях параметра k интервал (x 2; x 1) содержит промежуток (-1; 2), где x 1 и x 2 – корни уравнения (k+2)x 2+(k-3)x+k-6=0 a *f (-1)<0 a *f (2)<0 (k+2)(k+2 -k+3+k-6)<0 (k+2)(4 k+8+2 k-6+k-6)<0 (k+2)(k-1)<0 (k+2)(7 k-4)<0 -1 x 2 X 2 x 1 f (-1) f (2) -2 -2 1 4/7 k k Э Ответ: при k (-2; 4/7).

Рассмотрев все случаи расположения корней параболы, можно сделать вывод: зная условия расположения корней квадратного уравнения на числовой прямой, можно с помощью графика всегда составить такие неравенства, которые полностью отразят заданные условия задачи. Рассмотрим несколько задач, отражающих данную теорию.

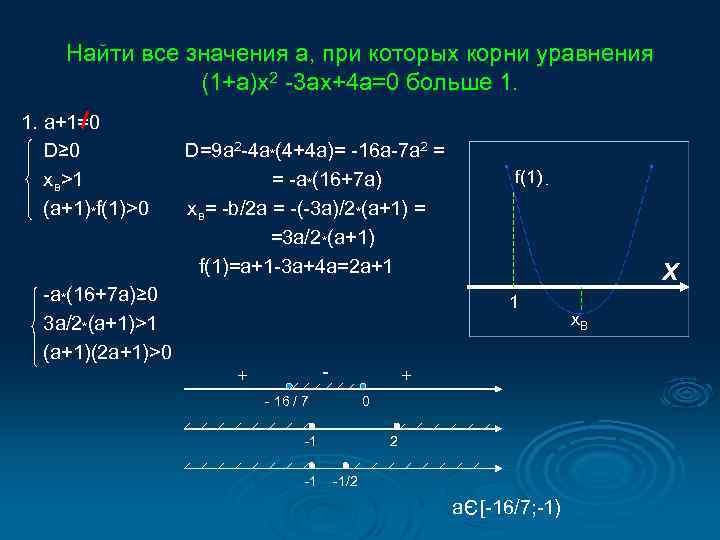Найти все значения а, при которых корни уравнения (1+а)х2 -3 ах+4 а=0 больше 1. D=9 a 2 -4 a*(4+4 a)= -16 a-7 a 2 = = -a *(16+7 a) xв= -b/2 a = -(-3 a)/2*(a+1) = =3 a/2 *(a+1) f(1)=a+1 -3 a+4 a=2 a+1 -a*(16+7 a)≥ 0 3 a/2*(a+1)>1 (a+1)(2 a+1)>0 f(1) X 1 - + + - 16 / 7 0 -1 -1 2 -1/2 Э 1. a+1=0 D≥ 0 xв>1 (a+1)*f(1)>0 a [-16/7; -1) x. В

2. Так как не сказано, что квадратное уравнение имеет корни больше 1, то рассмотрим случай, когда квадратное уравнение будет линейным: a+1=0 a= -1 (1 -1)x 2 – 3 x*(-1) – 4*(-1)=0 3 x-4=0 x=4/3 (4/3>1, следовательно х=4/3 является корнем уравнения) Ответ: а [-16/7; -1)V{4/3} Э

При каких значениях а уравнение (2 а-1)х2 +(3 -а)х+1=0 имеет два действительных корня меньше 2. Уравнение не может быть линейным, т. е. 2 а-1=0, так как в условии сказано, что уравнение имеет два корня. 2 а-1=0; a=1/2 f(2) 2 -8 a+4= D>0 D=9 -6 a+a Xв<2 =a 2 -14 a+13=(a-1)(a-13) (2 a-1)*f(2)>0 xв= -(3 -a)/2*(2 a-1)= X = (a-3)/2 *(2 a-1) 2 f(2)=(2 a-1)*4+(3 -a)*2+1= xв =6 a+3 (a-1)(a-13)>0 + + (a-3)/2*(2 a-1)<2 1 13 + (2 a-1)(6 a+3)>0 1/7 1/2 + + 1/2 ; -1/2)V(13; + ) 8 Ответ: a ( - 8 Э -1/2

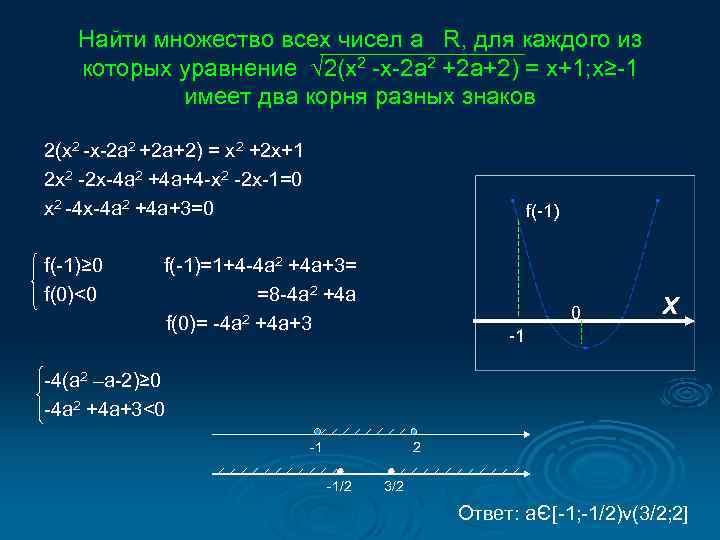Найти множество всех чисел а R, для каждого из которых уравнение √ 2(х2 -х-2 а 2 +2 а+2) = х+1; х≥-1 имеет два корня разных знаков 2(x 2 -x-2 a 2 +2 a+2) = x 2 +2 x+1 2 x 2 -2 x-4 a 2 +4 a+4 -x 2 -2 x-1=0 x 2 -4 x-4 a 2 +4 a+3=0 f(-1)≥ 0 f(0)<0 f(-1)=1+4 -4 a 2 +4 a+3= =8 -4 a 2 +4 a f(0)= -4 a 2 +4 a+3 0 X -1 -4(a 2 –a-2)≥ 0 -4 a 2 +4 a+3<0 -1 2 3/2 Э -1/2 Ответ: a [-1; -1/2)v(3/2; 2]

Найти все значения k, при которых оба корня уравнения kx 2 –(k+1)x+2=0 по абсолютной величине меньше 1. D=k 2 +2 k+1 -8 k=k 2 - 6 k+1 Xв= -b/2 a=(k+1)/(2 k) f(1)=k-k-1+2=1 f(-1)=k+k+1+2=2 k+3 k 2 - 6 k+1>0 (k+1)/(2 k)>-1 (k+1)/(2 k)<1 k*(2 k+3)>0 k>0 f(-1) D>0 x в>-1 xв<1 k *f(-1)>0 k *f(1)>0 k 2 - 6 k+1>0 (3 k+1)/(2 k)>0 (1 -k)/(2 k)<0 k*(2 k+3)>0 k>0 8 -1 1 + + 3 -2√ 2 - + - -1/3 -3/2 ) X xв + Э Ответ: k (3+2√ 2; + f(1) 3+2√ 2 + 0 0 + 1 +

Найти а, при которых все решения уравнения x 4 +(3 a-2)x 2(x+1)+(2 a 2 –a-3)(x+1)2=0 удовлетворяют условие -3≤х≤ 0 2. x+1=0; x= -1 1=0 O a=3/2 x 4 –(5 x 2(x+1))/2=0 x 2(x 2 -5 x/2 -5/2)=0 x=0 2 x 2 -5 x-5=0 x=(5+√ 65)/4 ( [-3; 0]) x=(5 -√ 65)/4 Э 1. x 2=0; x=0 2 a 2 -a-3=0 a= -1 x 4 -5 x 2(x+1)=0 x 2(x 2 -5 x-5)=0 x=(5+3√ 5)/2 ( [-3; 0]) x=(5 -3√ 5)/2 Э X 4 +(3 a-2)x 2(x+1)+(2 a 2 –a-3)(x+1)2 =0 (: x 2(x+1); x≠ 0; x≠ -1) x 2/(x+1)+(3 a-2)+(2 a 2 -a-3)(x+1)/x 2=0 x 2/(x+1)=t t+(2 a 2 -a-3)/t+3 a-2=0; t≠ 0

t 2+(3 a-2)t+(2 a 2 -a-3)=0 D=9 a 2 -12 a+4 -8 a 2 +4 a+12=a 2 -8 a+16=(a - 4)2 t 1=(2 -3 a+a-4)/2= -a-1 t 2=(2 -3 a-a+4)/2=3 -2 a x 2/(x+1)= -a-1 x 2/(x+1)=3 -2 a x 2+x(a+1)+(a+1)=0 x 2 –x(3 -2 a)-(3 -2 a)=0 D=a 2+2 a+10 -4 a-4= D=9 -12 a+4 a 2+12 -8 a= =a 2 -2 a-3=(a+1)(a-3) =4 a 2 -20 a+21=4(a-3/2)(a-7/2) f(-3)=9 -3 a-3+a+1= f(-3)=9+9 -6 a-3 -2 a= =7 -2 a =15 -8 a f(0)=a+1 f(0)=2 a-3 xв=-b/2 a=-(a+1)/2 xв=-b/2 a=(3 -2 a)/2 (a+1)(a-3)≥ 0 7 -2 a≥ 0 a+1≥ 0 -(a+1)/2≥-3 -(a+1)/2≤ 0 4(a-7/2)(a-3/2)≥ 0 15 -8 a≥ 0 2 a-3≥ 0 (3 -2 a)/2≥-3 (3 -2 a)/2≤ 0 f(-3) f(0) X -3 0 xв D ≥ 0 f(-3) ≥ 0 f(0)≥ 0 x в≥-3 xв≤ 0

(a+1)(a-3)≥ 0 a≤ 7/2 a≥-1 a≤ 5 a≥-1 + (a-7/2)(a-3/2)≥ 0 a≤ 15/8 a≥ 3/2 a≤ 9/2 a≥ 3/2 + -1 3 3/2 7/2 15/8 -1 3/2 9/2 5 -1 3/2 [3; 7/2] Э Э a 7/2 Ответ: a [3; 7/2]v{3/2}

При каких действительных значениях параметра β уравнение 2(β 2 +1)cos 2 x+4β 2 cosx+1=0 не имеет решений. -1 + 1 Э + β (-1; 1) 3. D=0 2β 4 – β 2 -1=0 β 2=1 β 2= -1/2 β=± 1 2(1+1)t 2 +4 t+1=0 (2 t+1)2=0; t= -1/2 2. f(-1)<0 f(1)<0 2β 2 +2 - 4β 2 +1<0 2β 2 +2 +4β 2+1>0 2β 2 – 3>0 6 β 2 + 3<0 ( β√ 2 -√ 3)(β√ 2+√ 3)>0 2 β 2 +1<0 O O Э cosx=t, |t|≤ 1 2(β 2+1) t 2+4β 2 t +1=0 1. D<0 D=4β 4 -2β 2 -2<0 β 2 =1 β 2 = -1/2 β=± 1 (решений нет) -1 f(-1) Ответ: β (-1; 1) X 1 f(1)

f(1) D>0 (a-1)*f(-1)<0 (a-1)*f(1)<0 7 -6 a>0 (a-1)*6<0 2(a-1)(2 a-1)<0 a<7/6 a<1 (a-1)(2 a-1)<0 f(-1) f(1) X -1 1 D<0 7 -6 a<0 a>7/6 a (7/6; + 1/2 1 7/6 1 + a (1/2; 1) ) 8 f(-1) X Э -1 1 sinx=t; |t|≤ 1 2. (a-1)t 2 +2(a -2)t +a+3=0 D/4=a 2 -4 a+4 -(a-1)(a+3)=a 2 -4 a+ +4 –a 2 -2 a+3=7 -6 a f(1)=a-1+2 a-4+a+3=2(2 a-1) f(-1)=a-1 -2 a+4+a+3=6 xв=-b/2 a=-(a-2)/(a-1)=(2 -a)/(a-1) Э 1. Найти а, при которых уравнение (а-1)sin 2 x+2(a-2)sinx+a+3=0 не имеет решений.

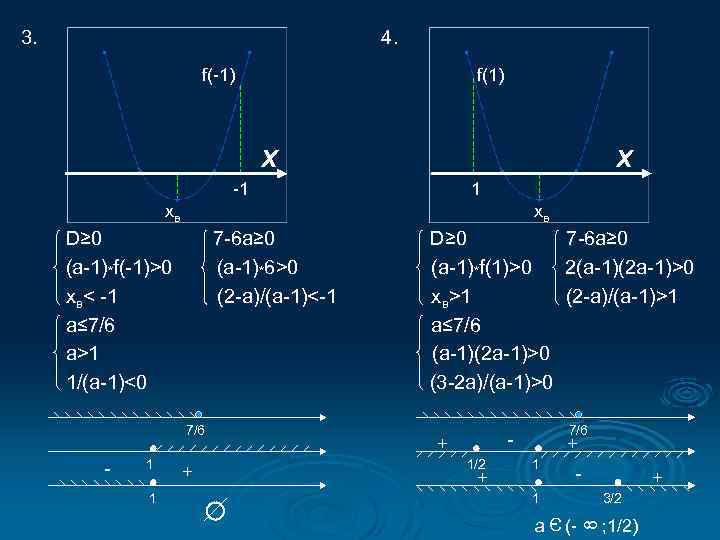3. 4. f(-1) f(1) X X -1 1 xв xв 7/6 - 1 1 + D≥ 0 7 -6 a≥ 0 (a-1)*f(1)>0 2(a-1)(2 a-1)>0 x в>1 (2 -a)/(a-1)>1 a≤ 7/6 (a-1)(2 a-1)>0 (3 -2 a)/(a-1)>0 7/6 - + 1/2 + + 1 - 1 a + 3/2 (- 8 7 -6 a≥ 0 (a-1)*6>0 (2 -a)/(a-1)<-1 Э D≥ 0 (a-1)*f(-1)>0 xв< -1 a≤ 7/6 a>1 1/(a-1)<0 ; 1/2)

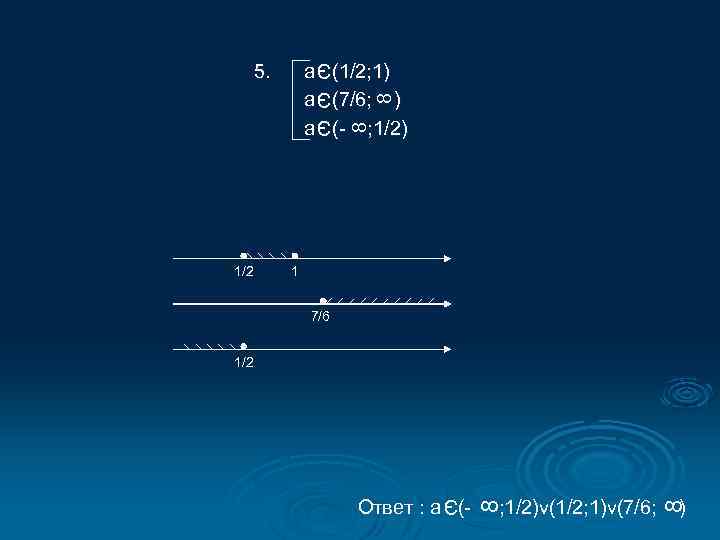8 Э Э Э 1/2 a (1/2; 1) a (7/6; ) a (- ; 1/2) 8 5. 1 7/6 1/2 ) 8 ; 1/2)v(1/2; 1)v(7/6; 8 Э Ответ : a (-

Литература: 1) 2) 3) «Квадратный трёхчлен в задачах» Дорофеев Г. В. «Алгебраические уравнения и неравенства» А. И. Азаров, О. М. Гладун, В. С. Федосенко «Подводные рифы экзаменов» А. Г. Мерзляк, В. Б. Полонский, М. С. Якир