Живые преобразования графиков.pptx
- Количество слайдов: 42

Муниципальное Общеобразовательное Учреждение «Средняя Общеобразовательная Школа № 236 г. Знаменск» Преобразования графиков функций Учитель математики Потапова Е. А.
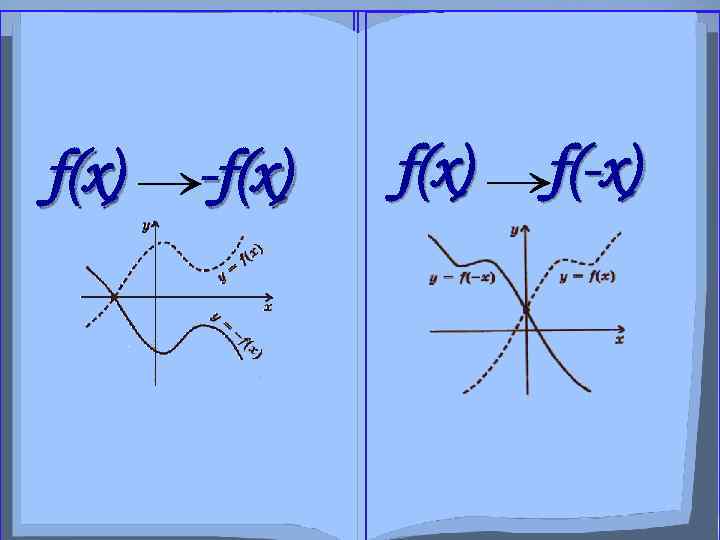
f(x) № 1 -f(x) Урок Преобразования симметрии f(x) f(-x) относительно осей х и у.
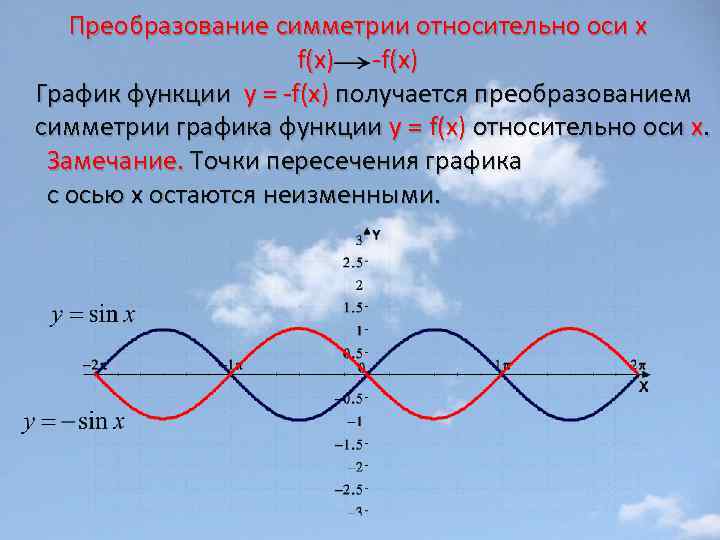
Преобразование симметрии относительно оси х f(x) -f(x) График функции у = -f(x) получается преобразованием симметрии графика функции у = f(x) относительно оси х. Замечание. Точки пересечения графика с осью х остаются неизменными.
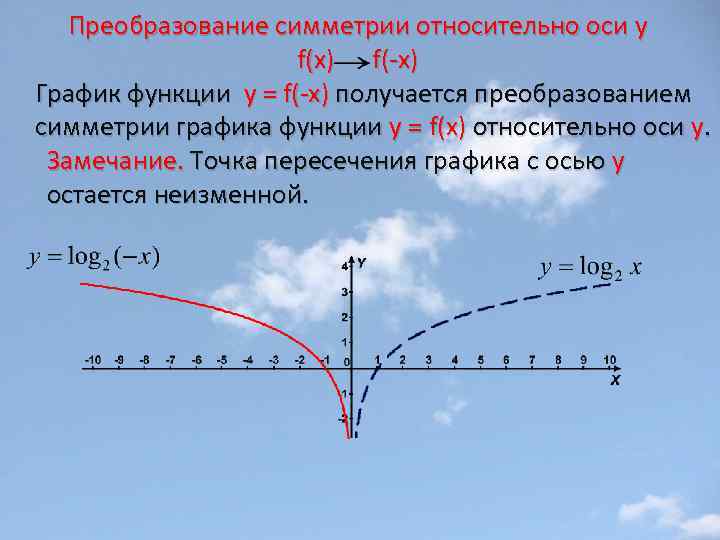
Преобразование симметрии относительно оси y f(x) f(-x) График функции у = f(-x) получается преобразованием симметрии графика функции у = f(x) относительно оси y. Замечание. Точкa пересечения графика с осью y остается неизменной.
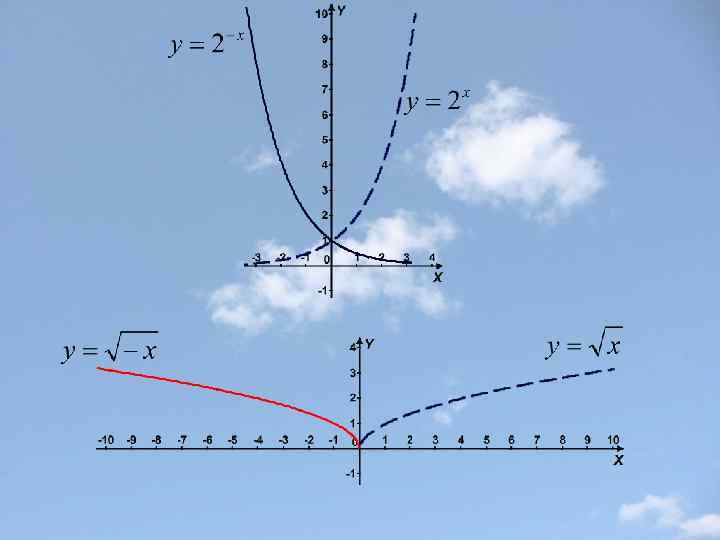

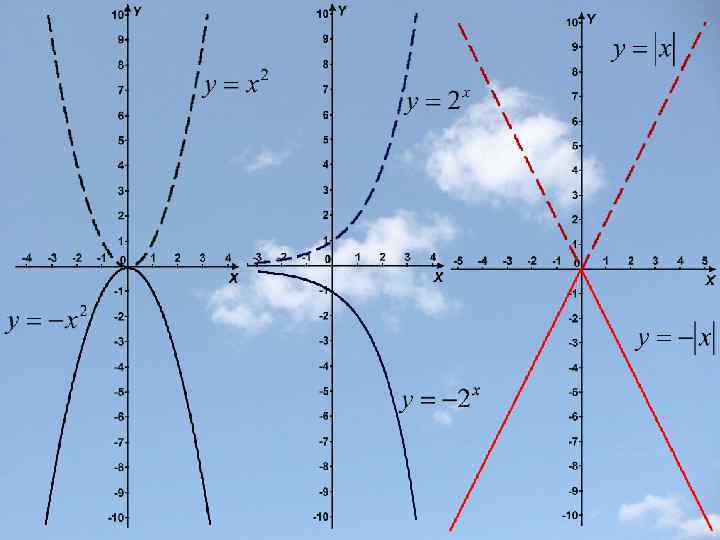
Замечание 1. График четной функции не изменяется при отражении относительно оси у, поскольку для четной функции f(-x)=f(x). Пример: (-x)2 = x 2.
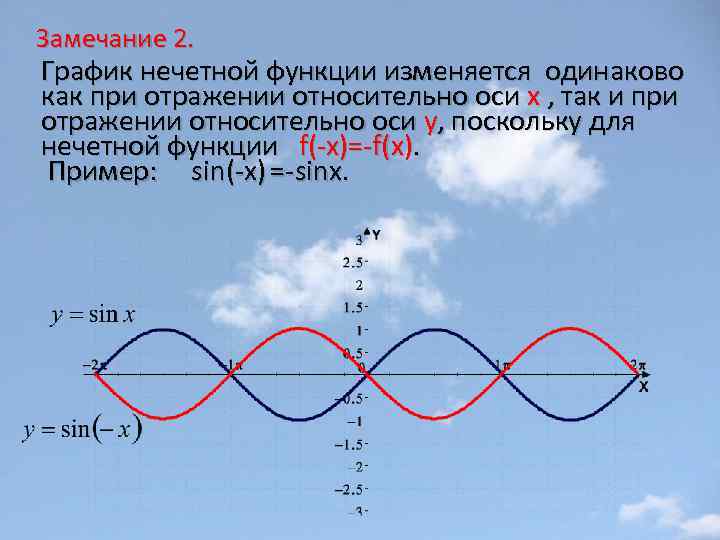
Замечание 2. График нечетной функции изменяется одинаково как при отражении относительно оси х , так и при отражении относительно оси у, поскольку для нечетной функции f(-x)=-f(x). Пример: sin(-x) =-sinx.
f(x) f(x-а) Урок № 2 Параллельный f(x) + b перенос вдоль осей х и у.
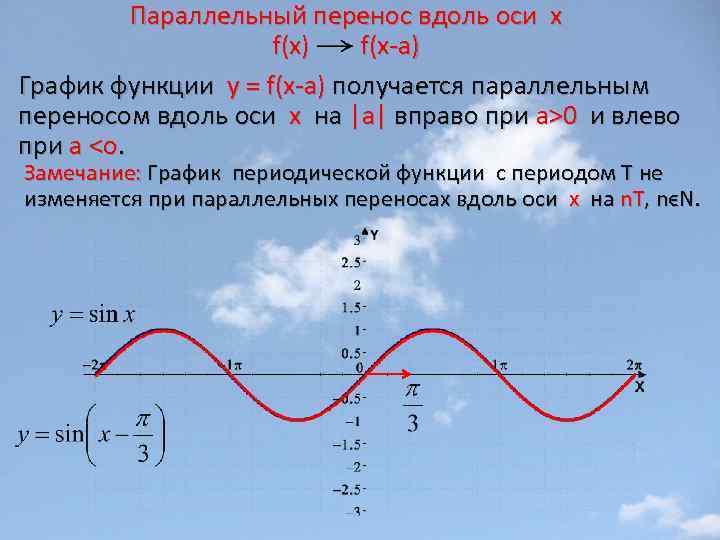
Параллельный перенос вдоль оси х f(x) f(x-а) График функции у = f(x-а) получается параллельным переносом вдоль оси х на |a| вправо при а>0 и влево при а <o. Замечание: График периодической функции с периодом Т не изменяется при параллельных переносах вдоль оси х на n. T, nϵN.
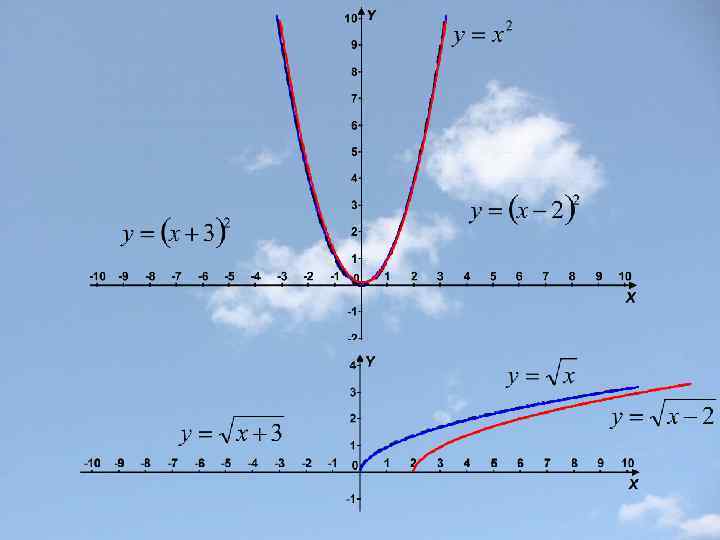
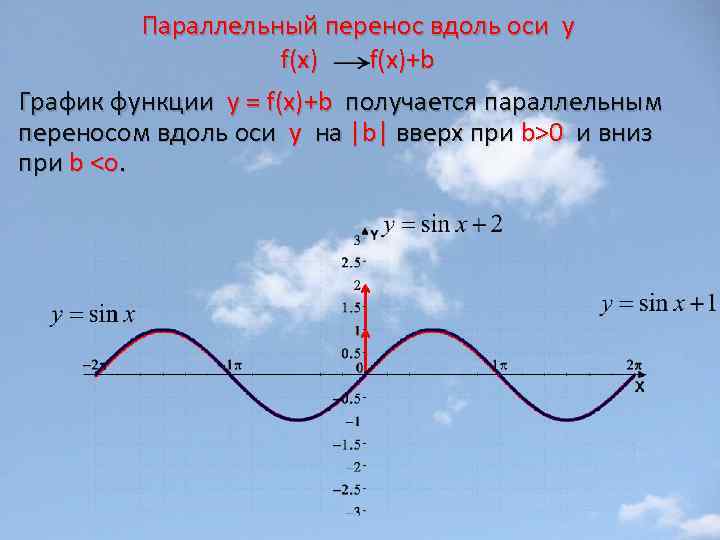
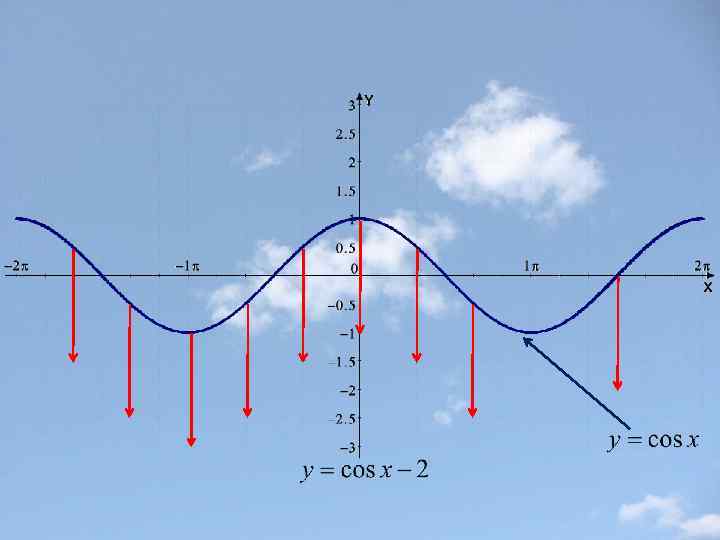
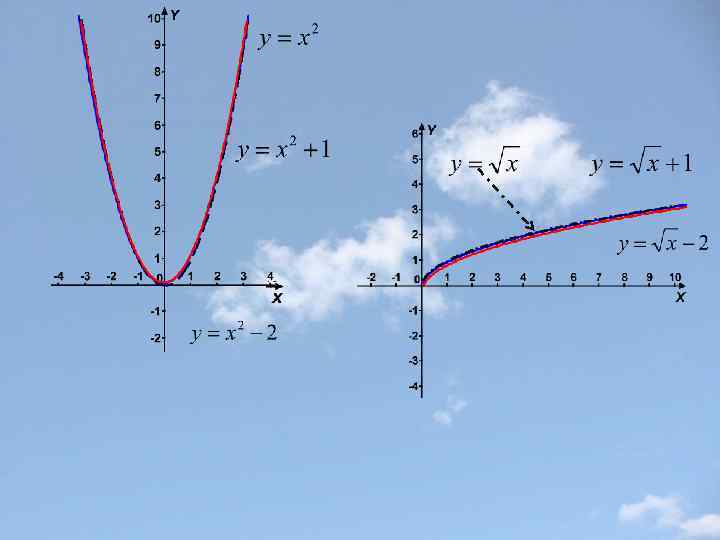
Параллельный перенос вдоль оси y f(x)+b График функции у = f(x)+b получается параллельным переносом вдоль оси y на |b| вверх при b>0 и вниз при b <o.
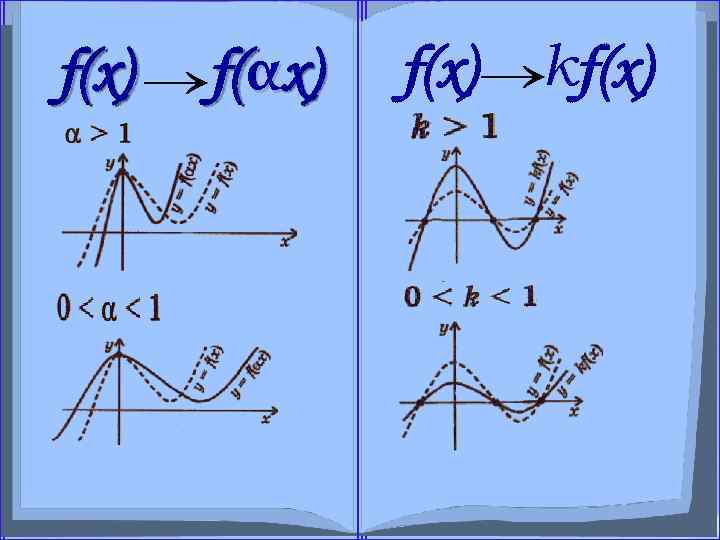
f(x) f(αx) Урок № 3 f(x) kf(x) Сжатие и растяжение вдоль осей x и у
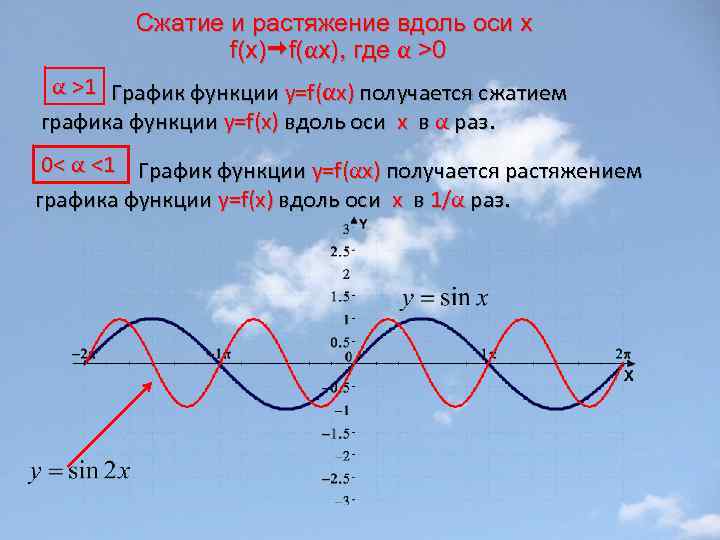
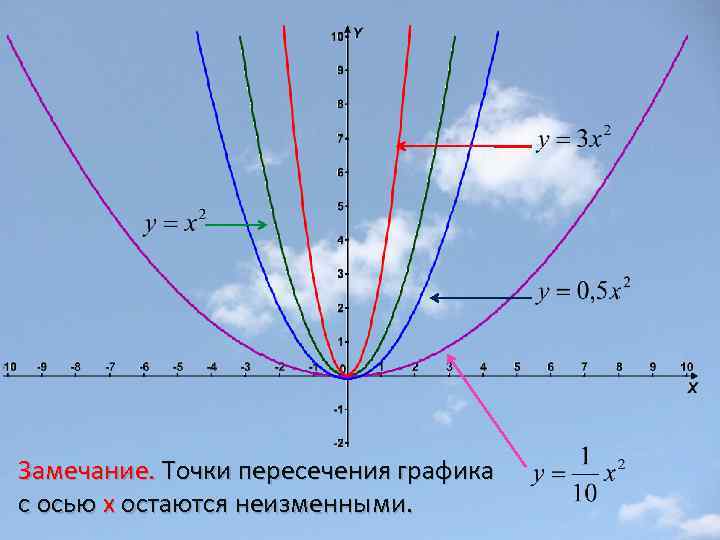
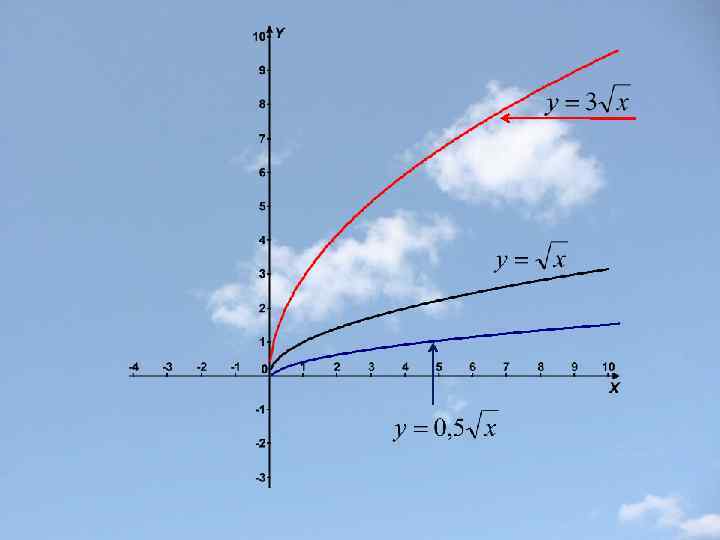
Сжатие и растяжение вдоль оси x f(x) f(αx), где α >0 α >1 График функции y=f(αx) получается сжатием графика функции y=f(x) вдоль оси х в α раз. 0< α <1 График функции y=f(αx) получается растяжением графика функции y=f(x) вдоль оси х в 1/α раз.
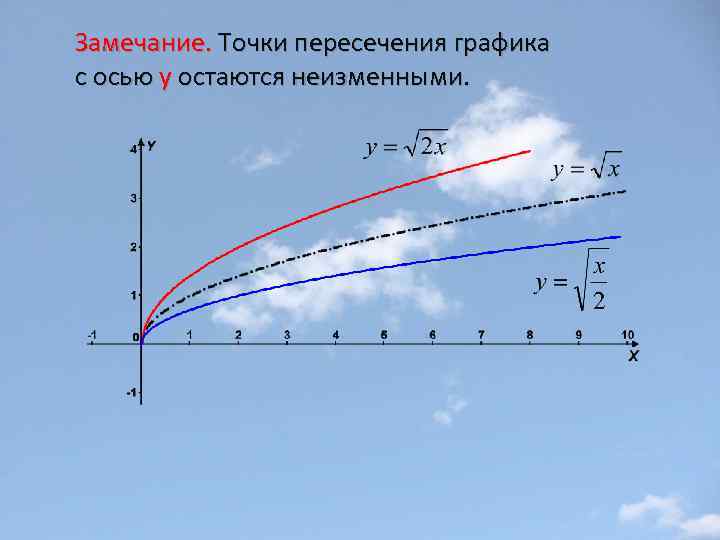
Замечание. Точки пересечения графика с осью y остаются неизменными.
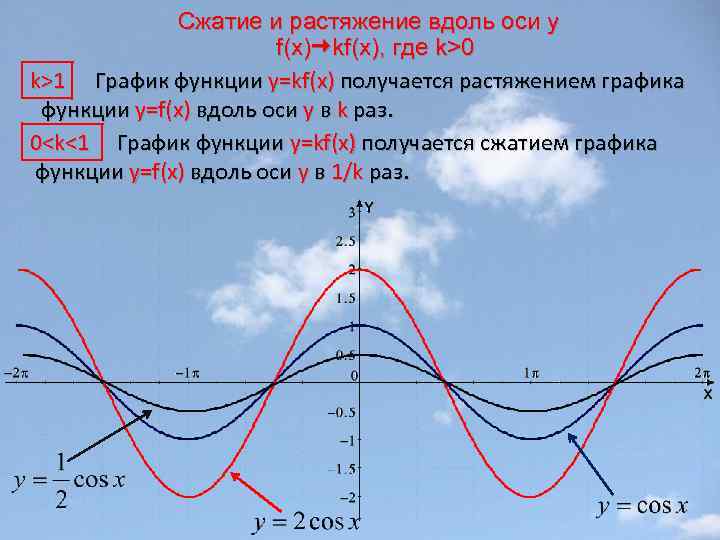
Сжатие и растяжение вдоль оси y f(x) kf(x), где k>0 k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз. 0<k<1 График функции y=kf(x) получается сжатием графика функции y=f(x) вдоль оси y в 1/k раз.
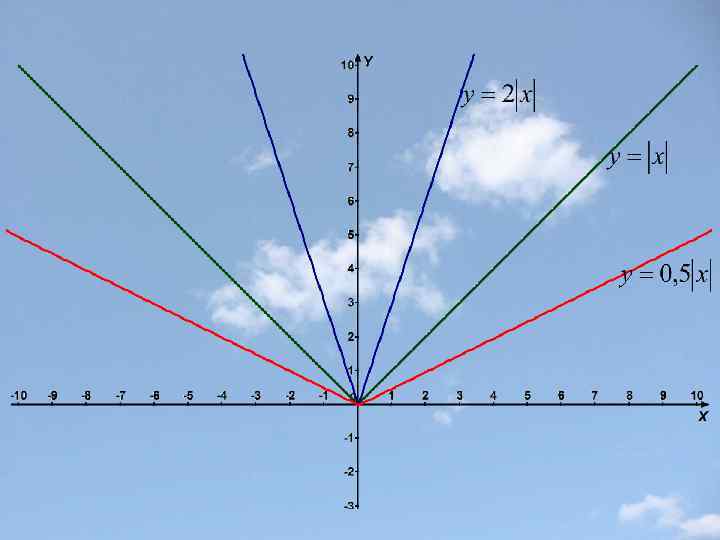
Замечание. Точки пересечения графика с осью x остаются неизменными.

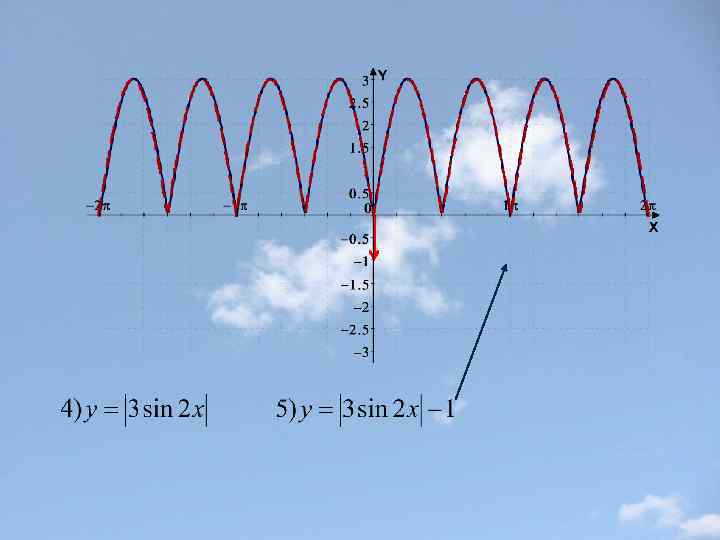
Урок № 4 Построение графиков функций y=f(|x|) и y=|f(x)|
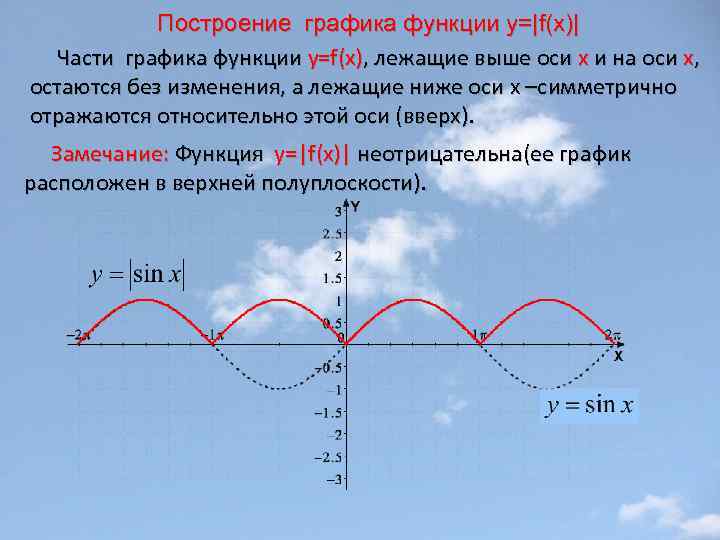
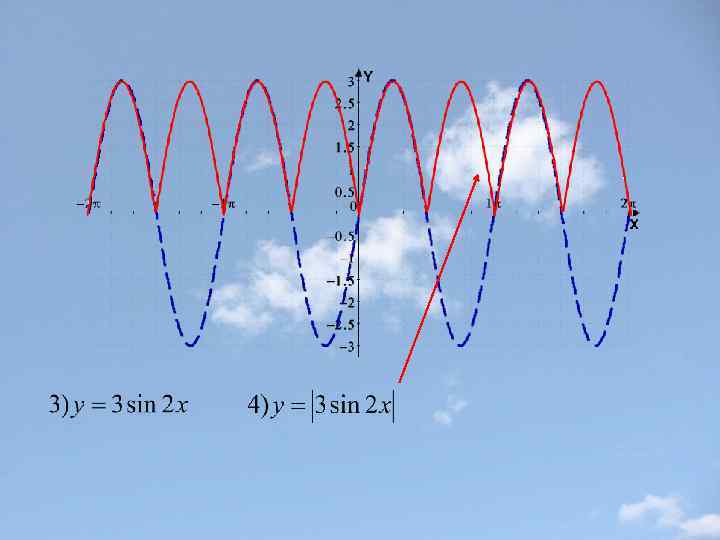
Построение графика функции у=|f(x)| Части графика функции y=f(x), лежащие выше оси х и на оси х, остаются без изменения, а лежащие ниже оси х –симметрично отражаются относительно этой оси (вверх). Замечание: Функция y=|f(x)| неотрицательна(ее график расположен в верхней полуплоскости).
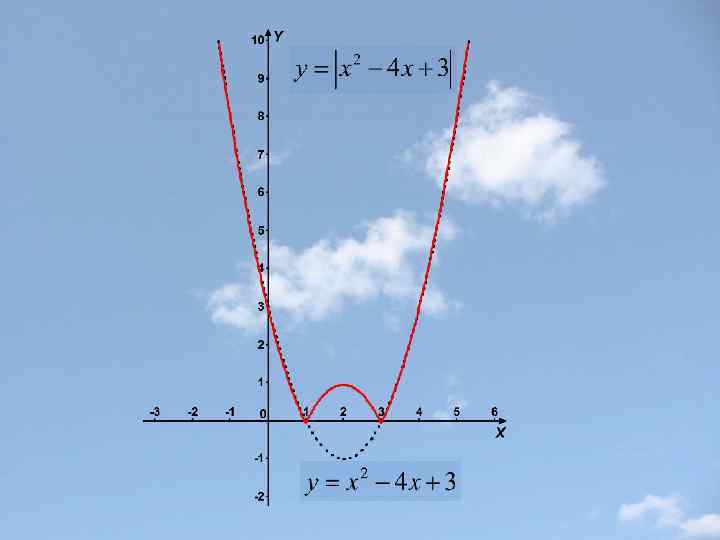
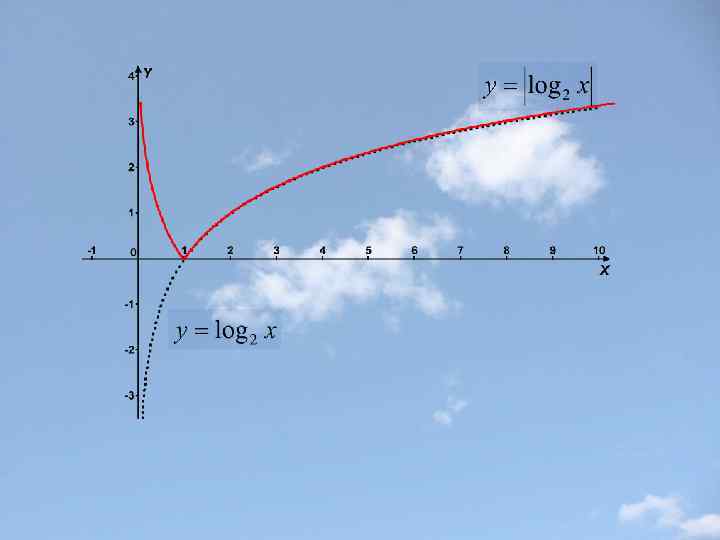
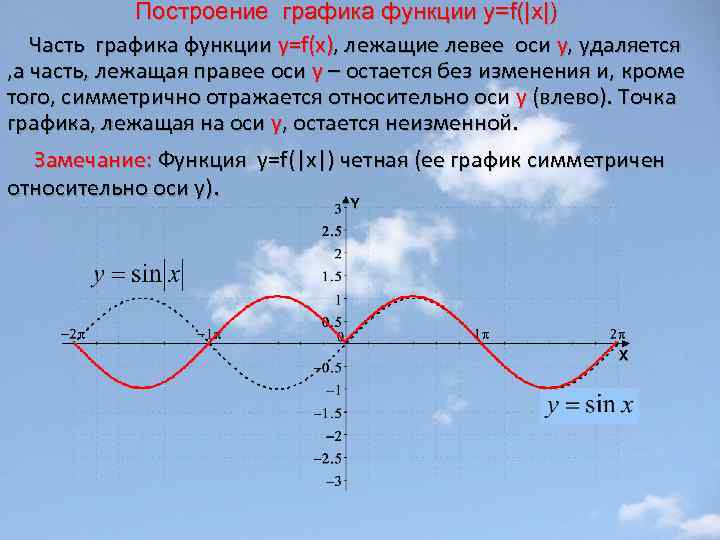
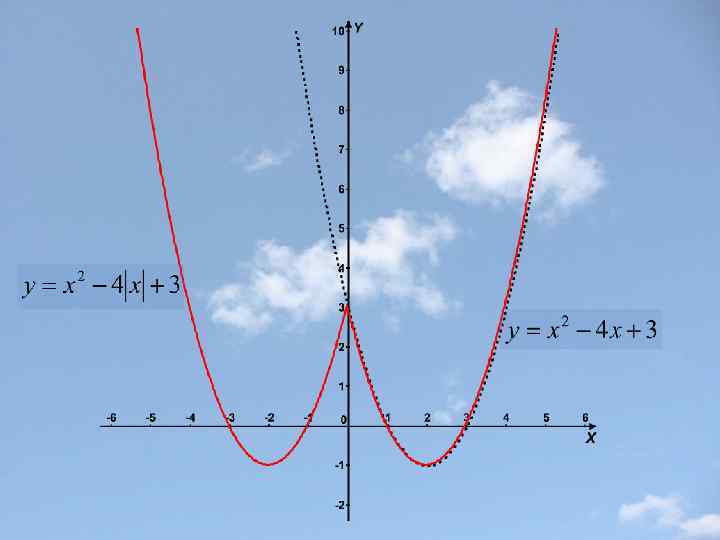
Построение графика функции у=f(|x|) Часть графика функции y=f(x), лежащие левее оси у, удаляется , а часть, лежащая правее оси у – остается без изменения и, кроме того, симметрично отражается относительно оси у (влево). Точка графика, лежащая на оси у, остается неизменной. Замечание: Функция y=f(|x|) четная (ее график симметричен относительно оси у).
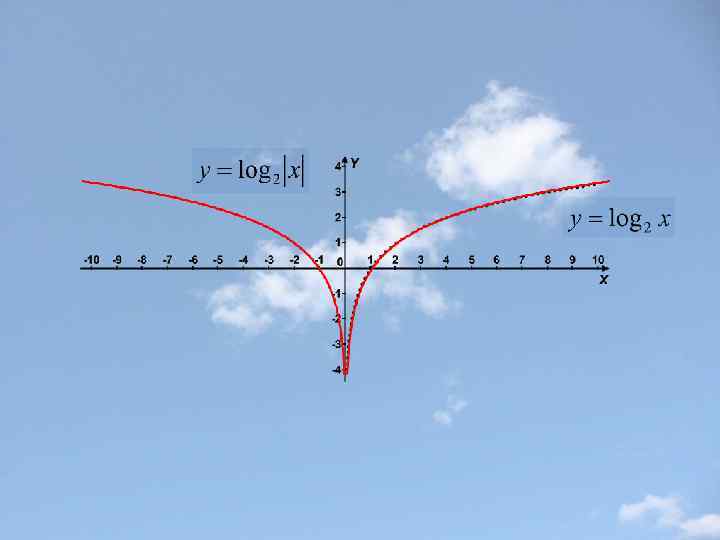

Урок № 5 Построение графика обратной функции
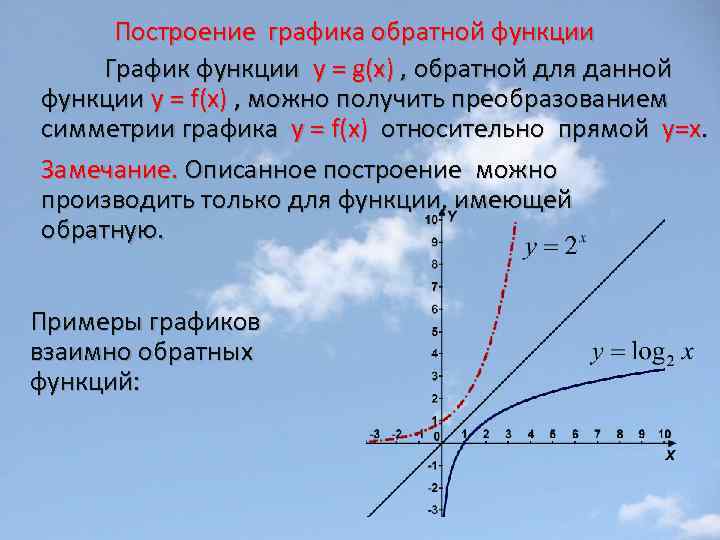
Построение графика обратной функции График функции у = g(x) , обратной для данной функции у = f(x) , можно получить преобразованием симметрии графика у = f(x) относительно прямой y=х. Замечание. Описанное построение можно производить только для функции, имеющей обратную. Примеры графиков взаимно обратных функций:
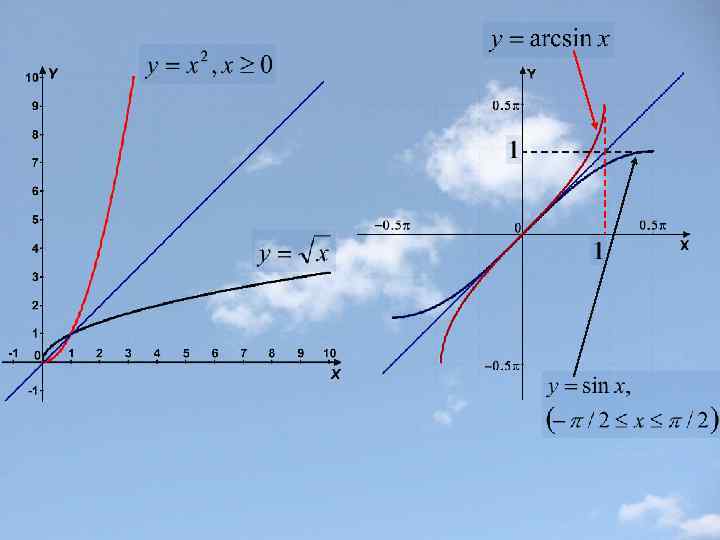
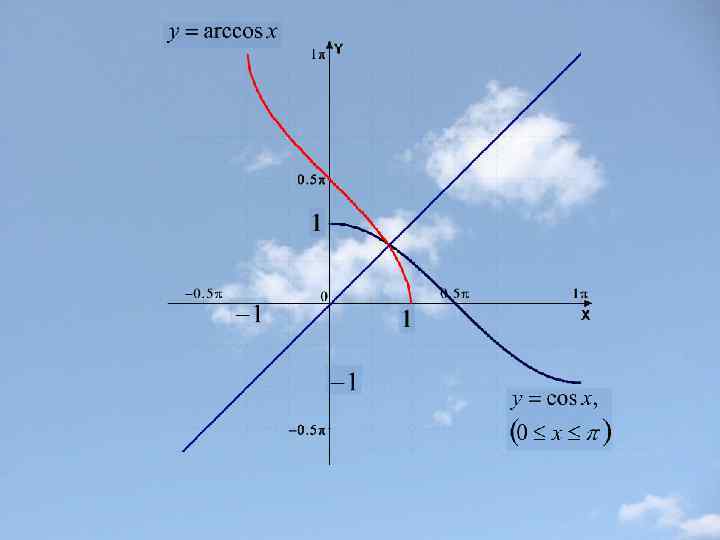
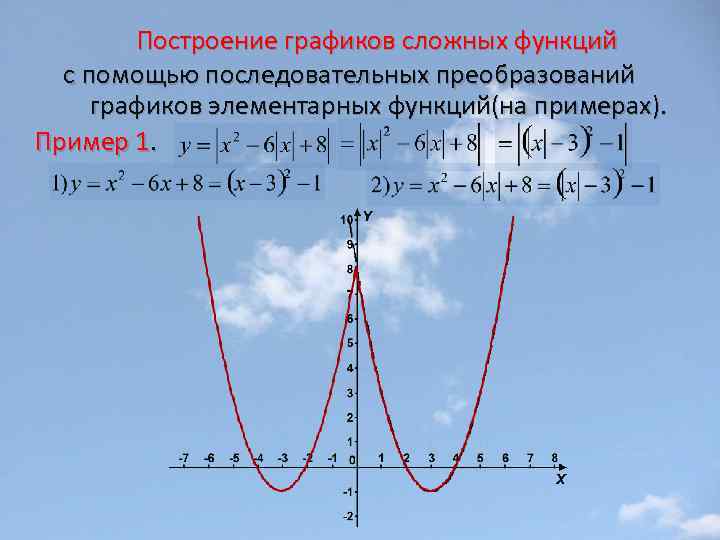
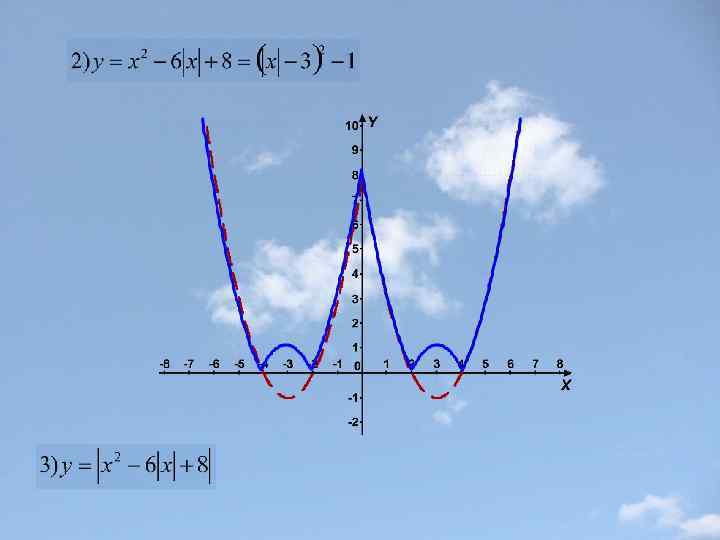
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций(на примерах). Пример 1.
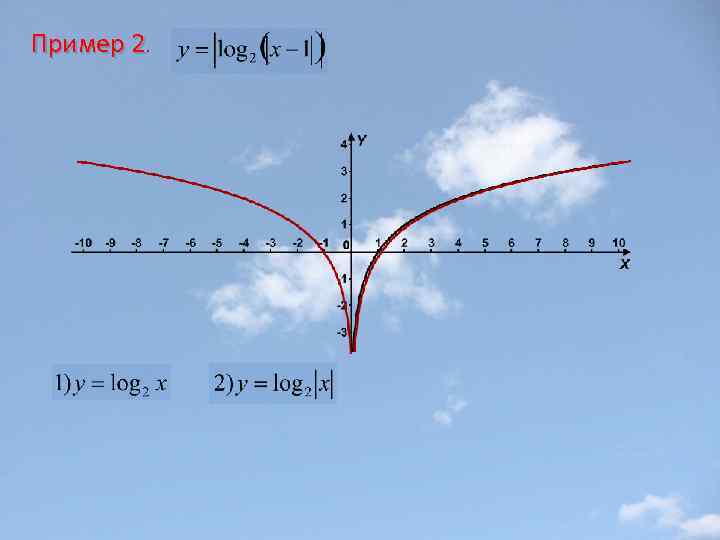
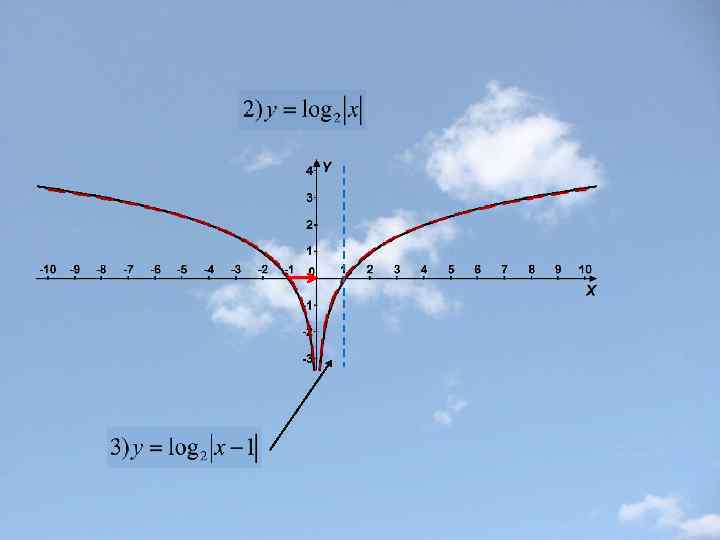
Пример 2.
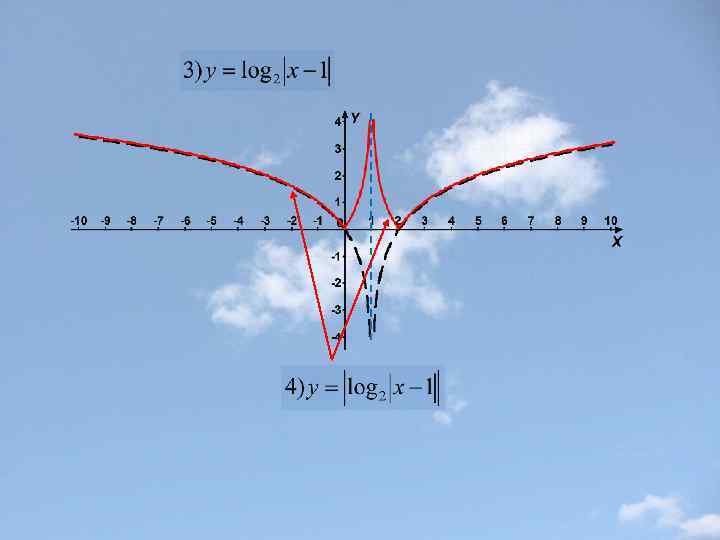
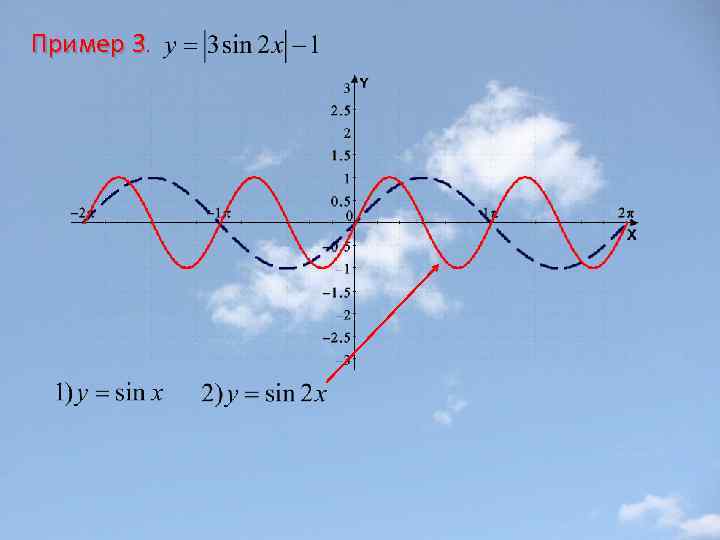
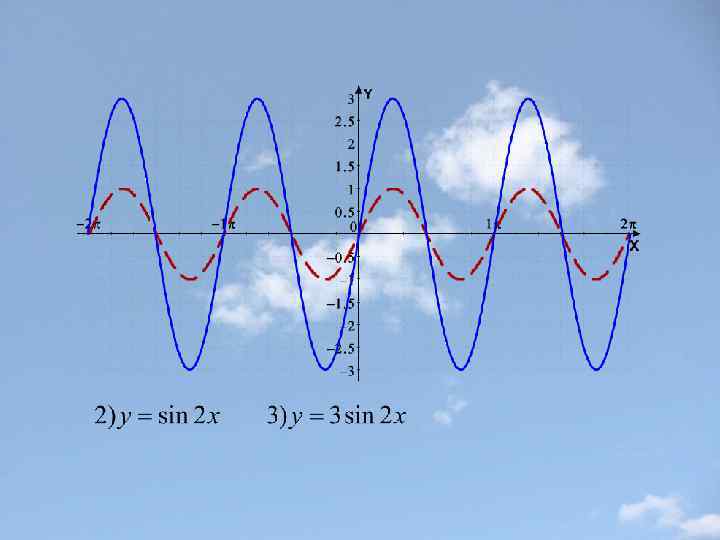
Пример 3.
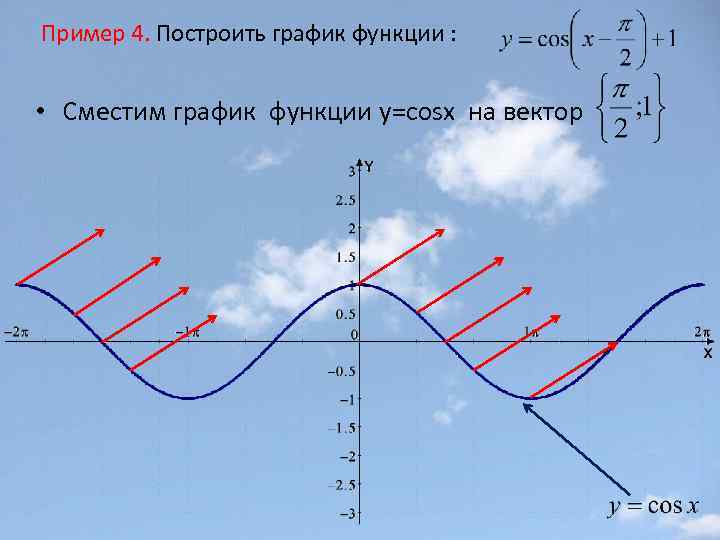
Пример 4. Построить график функции : • Сместим график функции y=cosx на вектор
Живые преобразования графиков.pptx