26d80a0d4f5b043c562a6982b1e2d000.ppt
- Количество слайдов: 23

Муниципальное образовательное учреждение «Средняя общеобразовательная школа № 22» Проект элективных курсов 9 классов «Дополнительные свойства арифметической и геометрической прогрессии и решение нестандартных заданий на применение этих свойств» Составитель: Макарова А. М. п. Билимбай 2011

Урок 3 Тема: « Арифметическая и геометрическая прогрессии (§ 28 (3 -1), § 30)» Цель: - ввести определения, аналитический способ задания, характеристические свойства прогрессии, - провести доказательство справедливости формул n-го члена каждой прогрессии. План I. Повторение. Фронтально а) понятие последовательности б) способы здания числовых последовательностей в) понятие среднего арифметического г) понятие среднего геометрического Записать для справки: а) а = а 1+а 2+…+аn, n б) b 1/b=b/b 2→ b=√b 1*b 2. II. Учено - познавательная работа учащихся по самостоятельному приобретению новых знаний.
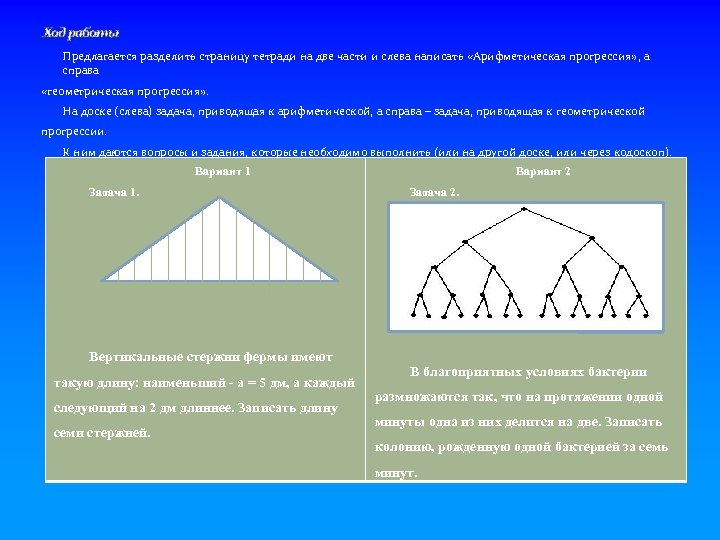
Ход работы Предлагается разделить страницу тетради на две части и слева написать «Арифметическая прогрессия» , а справа «геометрическая прогрессия» . На доске (слева) задача, приводящая к арифметической, а справа – задача, приводящая к геометрической прогрессии. К ним даются вопросы и задания, которые необходимо выполнить (или на другой доске, или через кодоскоп). Вариант 1 Задания даются по вариантам: Задача 1. Вертикальные стержни фермы имеют такую длину: наименьший - а = 5 дм, а каждый следующий на 2 дм длиннее. Записать длину семи стержней. Вариант 2 Задача 2. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Записать колонию, рожденную одной бактерией за семь минут.

1) Записать последовательность в соответствии с условием задачи. 2) Найти разность d между предыдущим и последующим членами последовательности в первой задаче, и частное q от деления последующего члена на предыдущее во второй задаче. 3) Записать эти последовательности рекуррентным способом. 4) Дать определение арифметической (геометрической) прогрессии. Выполнить вывод формул n-го члена прогрессий. 5) Найти среднее арифметическое (геометрическое) чисел 2 и 8. Записать найденное число с данными в прядке возрастания. Образуют ли эти числа арифметическую (геометрическую) прогрессию? 6) Справедлива ли такая зависимость для трех последовательных членов рассматриваемых последовательностей? 7) Доказать, что для членов арифметической прогрессии справедлива закономерность: аn = an-1 + an+1 , n > 1, а для членов геометрической прогрессии – закономерность 2 bn = √bn-1*bn+1, n>1. Работа выполняется сразу для обеих прогрессий.

Записи ответов учащихся 1) 5; 7; 9; 11; 13; 15; 17; 1) 1; 2; 4; 8; 16; 32; 64; 2) а 2 - а 1=2 а 3 – а 2 =2 … аn+1 – аn=d 2) в 2/в 1 = 2 в 3/в 2 = 2 … вn+1/вn = q 3) а 2 = а 1+ 2 а 3 = а 2+ 2 … аn+1= аn+ d 3) в 2=в 1*q в 3=в 2* q … вn+1=вn* q 4) Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену сложенному с одним и тем же числом называется предшествующему члену умноженному на одно и то же число, не равное 0 называется арифметической геометрической Прогрессией. Вывод формулы n – го члена а 2 = а 1+ d а 3 = а 2+ d= a 1+ 2 d а 4 = а 3+ d = a 1+ 3 d … аn = а 1+(n-1)*d в 2=в 1*q в 3=в 2*q=b 1*q 2 в 4=в 3*q=b 1*q 3 … вn=в 1*qn-1 5) 2 + 8 =5; 2; 5; 8; n 5) √ 2*8 = 4; 2; 4; 8 6) 5 + 9 = 7; 7 + 11 = 9… n 2 6) √ 1*4 = 2; √ 2*8 = 4… 7) аn+1= аn+ d, аn-1= аn - d (определение) ↓ аn= аn+1 - d, аn = аn-1+ d, 2 an= an+1 - d + an-1 + d ↓ a = a + a 7) вn+1 = вn* q; вn-1 = вn/q (определение) ↓ q = bn+1 q = bn bn-1 bn+1 = bn → вn = вn+1* bn-1 → bn = √вn+1* bn-1 b b

Цель: -показать приемы решения нетипичных заданий на применение понятий, «сумма членов» , -показать прием нахождения сумм конечных и бесконечных числовых последовательностей, - познакомить с понятием «ряды» , их свойствами, а также приемом использования свойств прогрессий при решении олимпиадных задач и задач повышенной трудности. Воспитательная задача: прививать интерес к истории развития математических понятий, самостоятельность мышления, умение справляться с решением сложных задач путем логически обоснованных преобразований (без формул). Тематический план уроков (Занятия идут параллельно с изучением темы, а число уроков сокращено за счет подачи темы «арифметическая прогрессия» одновременно с темой «геометрическая прогрессия» , т. о. достигается метод сравнения свойств и характеристик частных видов последовательностей). 1. Числовая последовательность 2 ч 2. Арифметическая и геометрическая прогрессии 2 ч 3. Сумма членов (n - первых) прогрессий 3 ч 4. Бесконечно убывающая геометрическая прогрессия (примечание: в учебнике Л. Г. Мордковича нет этой темы) 1 ч 5. Уроки – практикумы по решению заданий по теме «последовательности» и «предел последовательности» 2 ч 6. Урок обобщения темы «прогрессии» 1 ч 7. Контрольная работа (или тест) 1 ч
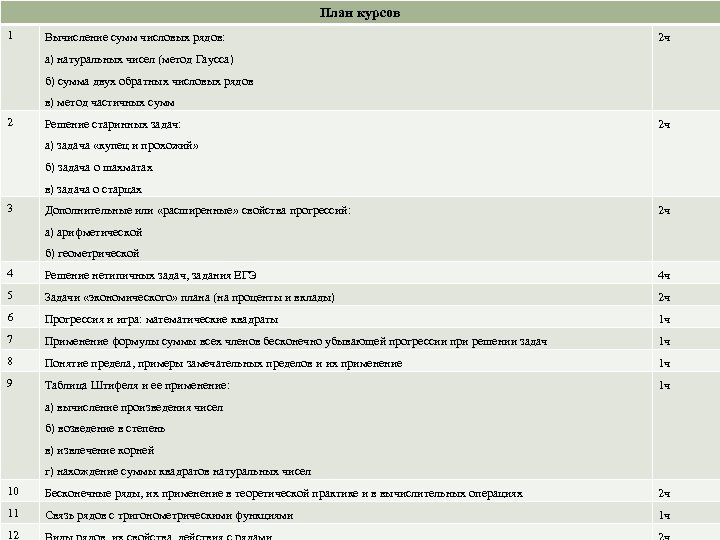
План курсов 1 Вычисление сумм числовых рядов: 2 ч а) натуральных чисел (метод Гаусса) б) сумма двух обратных числовых рядов в) метод частичных сумм 2 Решение старинных задач: 2 ч а) задача «купец и прохожий» б) задача о шахматах в) задача о старцах 3 Дополнительные или «расширенные» свойства прогрессий: 2 ч а) арифметической б) геометрической 4 Решение нетипичных задач, задания ЕГЭ 4 ч 5 Задачи «экономического» плана (на проценты и вклады) 2 ч 6 Прогрессия и игра: математические квадраты 1 ч 7 Применение формулы суммы всех членов бесконечно убывающей прогрессии при решении задач 1 ч 8 Понятие предела, примеры замечательных пределов и их применение 1 ч 9 Таблица Штифеля и ее применение: 1 ч а) вычисление произведения чисел б) возведение в степень в) извлечение корней г) нахождение суммы квадратов натуральных чисел 10 Бесконечные ряды, их применение в теоретической практике и в вычислительных операциях 2 ч 11 Связь рядов с тригонометрическими функциями 1 ч 12

Литература 1. Груденов Я. И. «совершенствование методики работы учителя математики» 2. Доброва О. К. и другие «методические рекомендации к курсу алгебры 7 -9 классов» 3. Коваленко В. Г. «дидактические игры на уроках математики» 4. Леонтьева М. Р. «самостоятельные работы на уроках математики» 5. Пичурин Л. Ф. «за страницами учебника алгебры» (книга для учащихся 7 -9 классов средней школы) 6. Савин А. П. энциклопедический словарь юного математика (для среднего и старшего возраста) 7. Эрдниев Б. , Эрдниев П. М. Укрупнение дидактических единиц как технология обучения 8. Журналы: «Математика в школе» «Квант» «Калейдоскоп»

Практическая часть Занятие 1 1. Задача, решенная Гауссом К. Ф. (1777 – 1855 гг) в возрасте 9 лет (есть фильм). Учитель, занятый проверкой работ учеников на уроке, решил дать такое задание, чтобы дети считали долго и были заняты: «вычислить сумму всех натуральных чисел от 1 до 40 включительно» , т. е. 1+ 2 + 3 + 4 + … + 39 + 40 – конечная числовая последовательность. Через минуту один изучеников воскликнул: «я уже решил!» . Большинство учеников после долгих подсчетов получили неверный результат, а в тетради у Гаусса было только одно число 820, но зато верное. Было ему тогда 9 лет. Решение (метод Гаусса) 1 + 2 + 3 + 4 + … + 38 + 39 + 40 = (1+ 40) + (2 + 39) + (3 + 38) + … = 41*20 = 820 20 сумм 2. Бревна сложили пирамидой, т. е. внизу 12 бревен, а в каждом следующем ряду на одно бревно меньше. Сколько бревен в пирамиде? Решение (метод суммы обратных рядов) Имеем S = 1 + 2 + 3 + … + 11+ 12 запишем в обратном порядке: S = 13 + 11 + 10 + … + 2 + 1 выполним сложение Получаем 2 S = 13 + … + 13 – всего 12 сумм, т. о. 2 S =13*12 S = 13*12 = 13*6 = 72 (бревна) 2

3. Найти сумму десяти слагаемых, если а) S 10 = 3 + 3/22 + … + 3/29 б) S 10 = 1 – 2 + 4 – 8 + 16 – 32 + 64 - … - 512 Решение Применим правило частичных сумм, т. е. разделим ряд так, чтобы первое слагаемое осталось, а из оставшейся суммы вынесем общий множитель: а) S 10 = 3 + ½*(3 + 3/2 + … + 3/28) = 3 + ½* (S 10 -3/28) → S 10 = 3 + 1/2*S 10 - 3/29 или 1. Раскрыли скобки. 2. Переносим S 10 из правой части в левую. 3. Решаем уравнение: ½* S 10 = 3 – 3/29 │ *2 S 10 = 6 – 3/28 (28 = 25 * 23 = 32 * 8 = 256) S 10 = 6 – 3/256 = 5*253/256 Ответ: 5*253/256 В) S 10 = 1 – 2 + 4 – 8 + … - 512 = 1 – 2* (1 – 2 + 4 – 8 + …+ 256) → S 10 = 1 - 2*( S 10 + 512) S 10 = 1 - 2 S 10 – 1024 S 10 = -2 S 10 – 1023 3 S 10 = – 1023 S 10 = – 341 Ответ: -341

Занятие 2 Задача 1. «Купец и прохожий» (№ 524 задачник) Однажды незнакомец постучал в окно к богатому купцу и предложил такую сделку: «я буду ежедневно в течение 30 дней приносить тебе по 100000 рублей. А ты мне в первый день за 100000 р дашь 1 копейку, во второй – 2 коп. и так будешь увеличивать предыдущее число денег. Если тебе выгодна сделка. То с завтрашнего дня начнем…» Купец обрадовался такой удаче. Он подсчитал. Что за 30 дней получит 3000000 (3 млн. р. ) рублей = 3*10 6. на следующий день они пошли к нотариусу и узаконили сделку. Кто в этой ситуации выиграл? Докажите! Решение 229 1 + 2 + 4 + 8 + 16 + … + 2 2 9 = 1 + 2*(1 + 2 2 + … + 2 2 8 ) → S = 1 + 2*(S-2 2 8 ) → S = 1 + 2 S - 2 2 9 → 2 S - S = – 1 → S = 2 2 9 - 1 (искомое количество денег) Ответ: S = 2 3 0 – 1 рублей отдал купец. 100 Задача 2. Легенды об индийском царе Шерами и изобретателе шахмат Сета. Оплата за обучение игре в шахматы: на первую клетку 1 росинку, на вторую – две, на третью – 4 и т. д. Решение а) Л. Н. Толстой решал эту задачу так: 1 клетка – 1 2 клетка – 2 3 клетка – 4 4 клетка – 8 … 33 – 4294967296 34 – 8589934592 35 – 17179869184 36 – 34359738369 … 9223372036854775808 и перевел в пуды: в одном пуде 40000 зерен (1 пуд -16, 4 кг), то на последней клетке вышло 230584300921369 пудов. Общее число зерен 18446744073706551615 штук б) Решение, в общем виде, аналогично решению задачи 1. S = 2 + 2 3 + … + 2 6 3 = 2 6 4 - 1 (решена в 973 – 1050 гг. хорезмским математиком Бируни)

Задача 3 Шел Кондрат в стольный град, а навстречу ему 7 стариков, у каждого по 7 костылей, на каждом костыле по 7 крюков на каждом крюке по 7 суков, на каждом сучке по 7 кошелей, в каждом кошеле по 7 пирогов, в каждом пироге по 7 воробьев. Сколько всего? Решение 7 + 49 + 343 + … и т. д. S = (7 5 -1) * 7/6 = 7/6*(7 5 -1) = 137256 Ответ: 137256 Занятие 3 Тема: «Арифметическая прогрессия» Задание 1 Дано: (а n ) – арифметическая прогрессия, а 1 = 7 а 1 6 = 67 Найти: α Доказать: d = a m - a n m - n

Решение 1 способ: побробный - через формулу а n = a 1 + d(n – 1) 2 способ: d = a 1 6 – a 1 16 – 1 ответ = 67 – 7 = 4 15 4 вывод а m = a 1 + (m – 1)d а n = a 1 + (n – 1)d а m - a n = (m - 1)d - (n – 1)d ↓ а m - a n = d(m – 1 – n + 1) ↓ а m - a n =d(m – n) → d = am - an m – n Задание 2 Доказать а n + a m = a k + a p – верно, если n + m = k + p Задание 3 «Геометрическая прогрессия » Доказать: в m * b n = b k * b p , если m + n = k + p

Занятие 4 Тема: «Решение нетипичных задач» 1. В сутках 24 часа. Часы с «боем» бьют каждый раз столько, сколько показывает часовая стрелка и каждые полчаса. Сколько всего ударов сделают часы (или кукушка). Решение Время от 1 до 12; 24 удара в сутки за каждые 30 минут 1, 2, 3, … 12 – (а n ) – арифметическая прогрессия n = 12, a 1 = 1, a n = 12 S 1 2 = 12 + 1 * 12 = 13*6 = 78 (ударов) – за полусуток 2 78*2 = 156 (ударов) - за сутки (без боя через 30 минут) S = 156 + 24 = 180 ударов за сутки. Ответ: 180 ударов. 2. Из пункта А в пункт В одновременно вышел пешеход и выехал велосипедист. Велосипедист, доехав за 1 час до пункта В возвращается обратно и встречает пешехода через 2/3 часа, затем снова едет до пункта В и, вернувшись обратно, встречает пешехода через 4/9 часа и т. д. он продолжает, пока пешеход не оказался в пункте В. Сколько времени был в пути пешеход? Решение 1 ч 2/3 ч 4/9 ч A B Пешеход 1; 2/3; 4/9; 8/27; … (вn) – геометрическая прогрессия S = 1 + 2/3 + 4/9 + 8/27 + … = 1 + 2/3(1 + 2/3 + 4/9 + 8/27 + …) = 1 + 2/3 S → S = 1 + 2/3 S → 1/3 S = 1 → S = 3 (часа) Ответ: 3 часа Задача 3 Найти сумму: 1 + ½ + ¼ + 1/8 + … Решение S = 1 + ½(1/2 + ¼ + 1/8 + …) = 1 + 1/2 S → S = 1 + 1/2 S → 1/2 S = 1, S = 2 Задача 4 Найти сумму 1 2 + 2² + 3² + … + 20² Ответ: 2870. о решения задачи (упражнение, закрепляющее метод частных сумм: дополнительно: задачник № 519, № 520 страница 108) – игровая ситуация: уйти с занятия, если сделать 1 шаг, полшага, четверть шага и т. д. Ответ: 2.
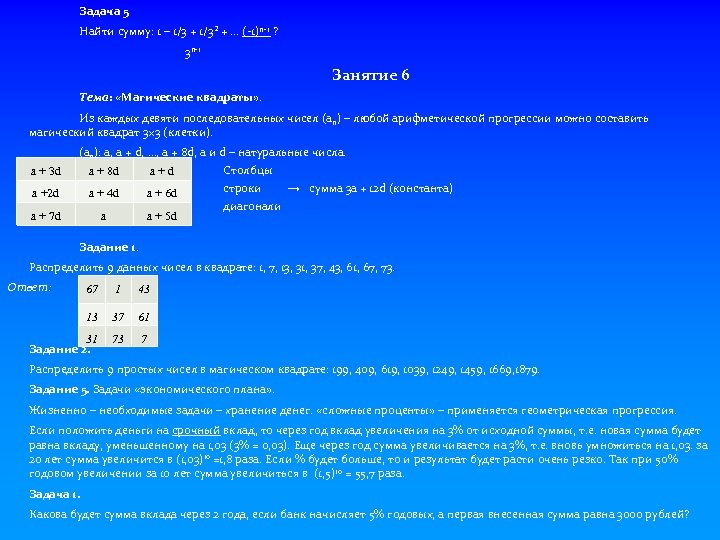
Задача 5 Найти сумму: 1 – 1/3 + 1/3² + … (-1)n-1 ? 3 n-1 Занятие 6 Тема: «Магические квадраты» . Из каждых девяти последовательных чисел (аn) – любой арифметической прогрессии можно составить магический квадрат 3× 3 (клетки). a + 3 d a +2 d a + 7 d (аn): а, а + d, …, a + 8 d, a и d – натуральные числа. Столбцы a + 8 d a + d строки → сумма 3 а + 12 d (константа) a + 4 d a + 6 d диагонали a a + 5 d Задание 1. Распределить 9 данных чисел в квадрате: 1, 7, 13, 31, 37, 43, 61, 67, 73. Ответ: 67 1 43 13 37 61 31 Задание 2. 73 7 Распределить 9 простых чисел в магическом квадрате: 199, 409, 619, 1039, 1249, 1459, 1669, 1879. Задание 5. Задачи «экономического плана» . Жизненно – необходимые задачи – хранение денег. «сложные проценты» – применяется геометрическая прогрессия. Если положить деньги на срочный вклад, то через год вклад увеличения на 3% от исходной суммы, т. е. новая сумма будет равна вкладу, уменьшенному на 1, 03 (3% = 0, 03). Еще через год сумма увеличивается на 3%, т. е. вновь умножиться на 1, 03. за 20 лет сумма увеличится в (1, 03)10 =1, 8 раза. Если % будет больше, то и результат будет расти очень резко. Так при 50% годовом увеличении за 10 лет сумма увеличиться в (1, 5)10 = 55, 7 раза. Задача 1. Какова будет сумма вклада через 2 года, если банк начисляет 5% годовых, а первая внесенная сумма равна 3000 рублей?

Решение (вn) – геометрическая прогрессия, в 1 = 3000, q = 1. 05, n = 2 (0. 05 = 5% - в 1, 05 раза) 1 год × 1, 05 2 год ___ 3000__ 3150, 00 рублей × 3150 ___4, 05___ + 1575 ___ 315_____ 330750 (р) = 3307 р 50 к Сколько належало за 2 года? 307 р 50 к Задача 2. (Задачник № 526, стр. 109) 1 – 10000 р 10% за квартал через год получили деньги с % 2 – 10000 р 45% - ежегодно Кто получил большую прибыль? Ответ: первый.
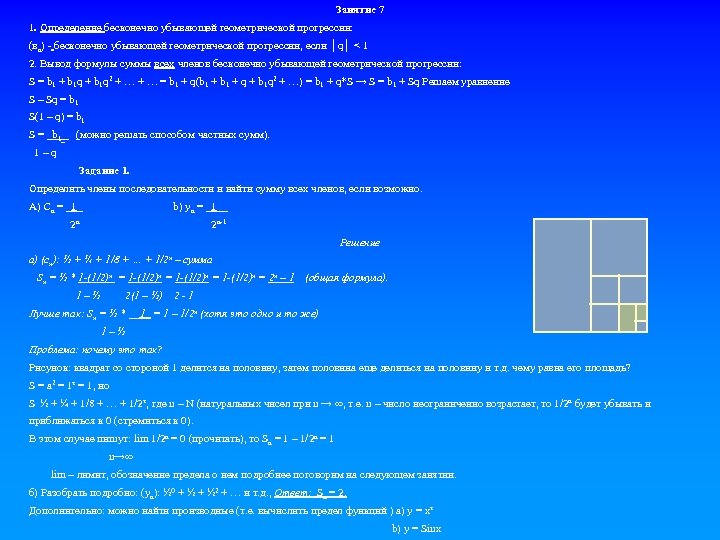
Занятие 7 1. Определение бесконечно убывающей геометрической прогрессии: (вn) - бесконечно убывающей геометрической прогрессии, если │q│ < 1 2. Вывод формулы суммы всех членов бесконечно убывающей геометрической прогрессии: S = b 1 + b 1 q 2 + … = b 1 + q(b 1 + q + b 1 q 2 + …) = b 1 + q*S → S = b 1 + Sq Решаем уравнение S – Sq = b 1 S(1 – q) = b 1 S = _b 1_ (можно решать способом частных сумм). 1 – q Задание 1. Определить члены последовательности и найти сумму всех членов, если возможно. А) Сn = _1_ b) yn = _1__ 2 n-1 Решение а) (сn): ½ + ¼ + 1/8 + … + 1/2 n – сумма Sn = ½ * 1 -(1/2)n = 2 n – 1 1–½ 2(1 – ½) (общая формула). 2 -1 Лучше так: Sn = ½ * __1_ = 1 – 1/2 n (хотя это одно и то же) 1–½ Проблема: почему это так? Рисунок: квадрат со стороной 1 делится на половину, затем половина еще делиться на половину и т. д. чему равна его площадь? S = a 2 = 1² = 1, но S ½ + ¼ + 1/8 + … + 1/2², где n – N (натуральных чисел при n → ∞, т. е. n – число неограниченно возрастает, то 1/2 n будет убывать и приближаться к 0 (стремиться к 0). В этом случае пишут: lim 1/2 n = 0 (прочитать), то Sn = 1 – 1/2 n = 1 n→∞ lim – лимит, обозначение предела о нем подробнее поговорим на следующем занятии. б) Разобрать подробно: (yn): ½ 0 + ½ 2 + … и т. д. , Ответ: Sn = 2. Дополнительно: можно найти производные (т. е. вычислить предел функций ) а) y = x² b) y = Sinx
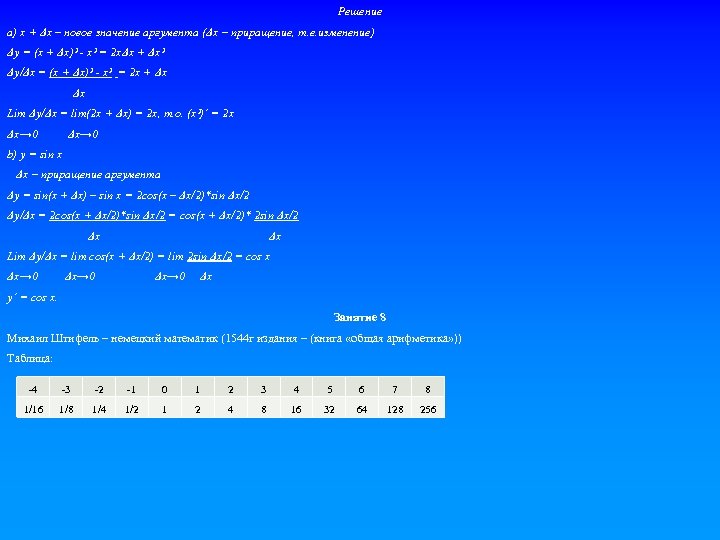
Решение а) x + Δx – новое значение аргумента (Δx – приращение, т. е. изменение) Δу = (x + Δx)² - x² = 2 xΔx + Δx² Δy/Δx = (x + Δx)² - x² = 2 x + Δx Δx Lim Δy/Δx = lim(2 x + Δx) = 2 x, т. о. (x²)´ = 2 x Δx→ 0 b) y = sin x Δx – приращение аргумента Δy = sin(x + Δx) – sin x = 2 cos(x – Δx/2)*sin Δx/2 Δy/Δx = 2 cos(x + Δx/2)*sin Δx/2 = cos(x + Δx/2)* 2 sin Δx/2 Δx Δx Lim Δy/Δx = lim cos(x + Δx/2) = lim 2 sin Δx/2 = cos x Δx→ 0 Δx y´ = cos x. Занятие 8 Михаил Штифель – немецкий математик (1544 г издания – (книга «общая арифметика» )) Таблица: -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 1/16 1/8 1/4 1/2 1 2 4 8 16 32 64 128 256

Задание 1 Определить виды последовательностей и их свойства: Ответ: (1) – (аn) – арифметическая прогрессия, с разностью 1 (2) – (вn) – геометрическая прогрессия со знаменателем 2 Связь между прогрессиями: а) пример 1: умножить ½*128 ½ → -1 (арифметическая прогрессия) -1 + 7 = 6 128 → 7 (геометрическая прогрессия) итог умножения б) пример 2: разделить 32 на 8: 32 → 5 (арифметическая прогрессия) 5 – 3 = 2 8 → 3 (геометрическая прогрессия) Ответ: 2 → 4; примеры легкие, но таблицу учащиеся могут расширить самостоятельно; в) пример 3: возвести в степень 4³ 4 → 2 – геометрическая прогрессия 2 * 3 = 6 против Ответ 6 → 64. Задание 2 Формулы: а) 1² + 2² + 3² + … + n² = n(n + 1)(2 n + 1) – сумма квадратов натуральных чисел, 6 в) Sn = n + 1 * n – сумма n натуральных чисел, 2 в) S 2 n-1 = n² - сумма n последовательных нечетных чисел. Привести примеры для применения формул.
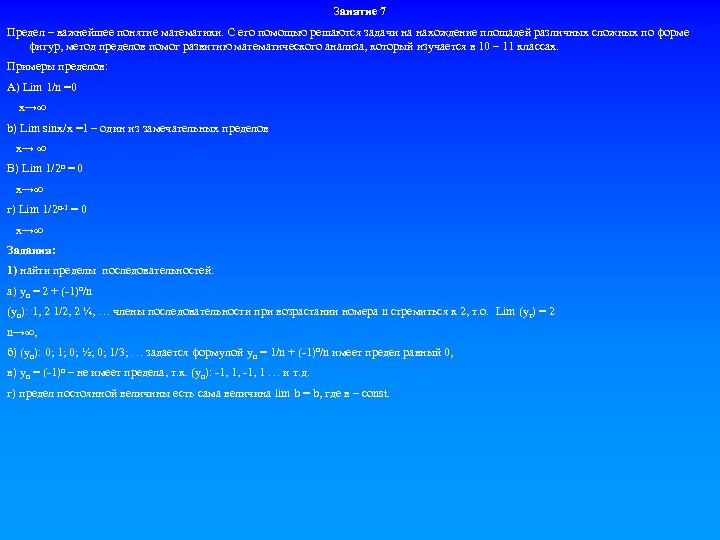
Занятие 7 Предел – важнейшее понятие математики. С его помощью решаются задачи на нахождение площадей различных сложных по форме фигур, метод пределов помог развитию математического анализа, который изучается в 10 – 11 классах. Примеры пределов: А) Lim 1/n =0 x→∞ b) Lim sinx/x =1 – один из замечательных пределов x→ ∞ В) Lim 1/2 n = 0 x→∞ г) Lim 1/2 n-1 = 0 x→∞ Задания: 1) найти пределы последовательностей: а) yn = 2 + (-1)n/n (yn): 1, 2 1/2, 2 ¼, … члены последовательности при возрастании номера n стремиться к 2, т. о. Lim (yт) = 2 n→∞, б) (yn): 0; 1; 0; ½; 0; 1/3; … задается формулой yn = 1/n + (-1)n/n имеет предел равный 0, в) yn = (-1)n – не имеет предела, т. к. (yn): -1, 1, -1, 1 … и т. д. г) предел постоянной величины есть сама величина lim b = b, где в – const.
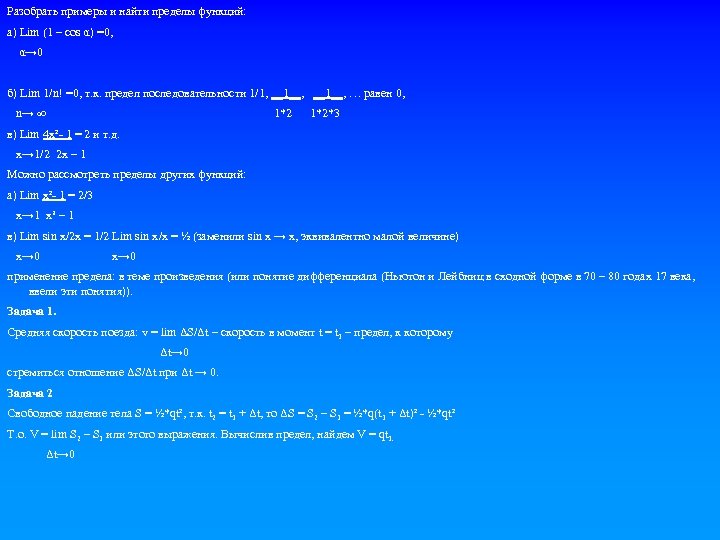
Разобрать примеры и найти пределы функций: а) Lim (1 – cos α) =0, α→ 0 б) Lim 1/n! =0, т. к. предел последовательности 1/1, __1__, … равен 0, n→ ∞ 1*2 1*2*3 в) Lim 4 x²- 1 = 2 и т. д. x→ 1/2 2 x – 1 Можно рассмотреть пределы других функций: а) Lim x²- 1 = 2/3 x→ 1 x³ – 1 в) Lim sin x/2 x = 1/2 Lim sin x/x = ½ (заменили sin x → x, эквивалентно малой величине) x→ 0 применение предела: в теме произведения (или понятие дифференциала (Ньютон и Лейбниц в сходной форме в 70 – 80 годах 17 века, ввели эти понятия)). Задача 1. Средняя скорость поезда: v = lim ΔS/Δt – скорость в момент t = t 1 – предел, к которому Δt→ 0 стремиться отношение ΔS/Δt при Δt → 0. Задача 2 Свободное падение тела S = ½*qt², т. к. t 2 = t 1 + Δt, то ΔS = S 2 – S 1 = ½*q(t 1 + Δt)² - ½*qt² Т. о. V = lim S 2 – S 1 или этого выражения. Вычислив предел, найдем V = qt 1. Δt→ 0

Занятие 9 М. Я. Выгодский, стр. 532 Определение: пусть дана последовательность чисел u 1, u 2, u 3, …, un, …; будем складывать эти числа в данном порядке, получим новую последовательность: S 1, S 2, S 3, … Sт, …, где: S 1 = u 1 S 2 = u 1 + u 2 S 3 = u 1 + u 2 + u 3 ………. Sn = u 1 + u 2 + … +un или u 1 + u 2 + u 3 +… + un + …, - эта сумма называется бесконечным рядом или (короче) рядом, числа u 1, u 2, u 3, …, - члены ряда. Виды рядов: сходящиеся и расходящиеся ряды. Определение: сходящийся ряд – его частичная сумма имеет конечный предел, он называется суммой ряда. Определение: если последовательность частичных сумм не имеет конечного предела, то ряд называется расходящимся. Примеры: а) 1 + ½ + ¼ + 1/8 + … + (1/2)n-1 + …. – сходящийся (его предел = 2), б) 1 + 2 + 3 + 4 + … + n + … - расходящийся, т. к. он имеет бесконечный предел Ряды положительные – все члены положительны, его частные суммы всегда имеют предел – конечный или бесконечный, в первом случае ряд сходится, во втором - расходится. 1 + __1__ + … + ___1__+ … cсходится. 2*5 3*5² n*5 n-1 Ряды знакопеременные: 1 – ½ + 1/3 – ¼ + … его члены стремятся к 0, но убывают не все время, т. е. он расходиться. Ряды можно умножать, интегрировать, дифференцировать. Степенные ряды: Sin x = x - __x³__ + ____x 5____ - _____x 7______ + … 1*2*3*4*5*6*7 cos x = 1 - _x²_ + ____x 4____ - ____x 6_____ + …, где х – радианная мера угла 1*2*3*4*5*6 дополнительные задания к теме: «дополнительные свойства прогрессий» . 1) Дано: (bn) – геометрическая прогрессия, в 2 = -5. Найти: а) в 1*в 3, б) в *в *в

Решение а) в 1*в 2 = в² 2 → в 1*в 2 = 25 → б) в 1*в 2*в 3 = 25*(-5) = -125 Что применили? Как проще? Вm* bn = bk* bp, где m + n = k + p 2) Дано: (вn): 2, 10, … - геометрическая прогрессия Найти: а) в 4*в 6, б) в 2*в 8…. . . , с) (в 5)², т. к. 4 + 6 = 10 2 + 8 = 10 5 * 2 = 10 Решение а 1 = 2, q = 5 a) в 4*в 6 = 2*5³ * 2* 55 = 4*58, b) 4*58, c) 4*58, почему? Ответ: Вm* bn = bm-1* bm+1, где n >0.
26d80a0d4f5b043c562a6982b1e2d000.ppt