Multiple variables regression.ppt
- Количество слайдов: 11

Multiple variables regression Множественная регрессия

The general purpose of multiple regression (the term was first used by Pearson, 1908) is to learn more about the relationship between several independent or predictor variables and a dependent or criterion variable. For example, a real estate agent might record for each listing the size of the house (in square feet), the number of bedrooms, the average income in the respective neighborhood according to census data, and a subjective rating of appeal of the house. Once this information has been compiled for various houses it would be interesting to see whether and how these measures relate to the price for which a house is sold. For example, you might learn that the number of bedrooms is a better predictor of the price for which a house sells in a particular neighborhood than how "pretty" the house is (subjective rating). You may also detect "outliers, " that is, houses that should really sell for more, given their location and characteristics.

The main formula of multiple regression is Y = a + b 1*X 1 + b 2*X 2 +. . . + bn*Xn And now let’s solve the example of problem. There are data of cars’ costs (resultative var y, th, tg), age of issue (car’s age is x 1 factor) and mileage(x 2 factor, th. km). Имеются данные о стоимости автомобилей (результативная переменная y, тыс. тг. ), о годе выпуска (возраст автомобиля – фактор х1, лет) и о пробеге (фактор х2, тыс. км):
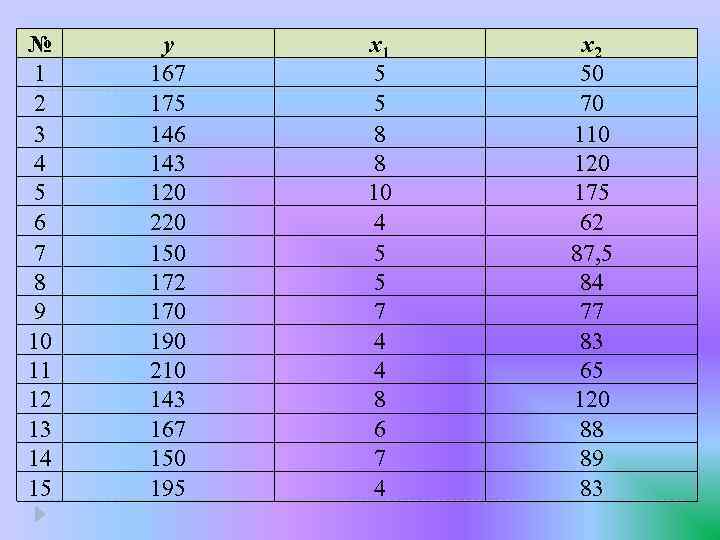
№ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 y 167 175 146 143 120 220 150 172 170 190 210 143 167 150 195 x 1 5 5 8 8 10 4 5 5 7 4 4 8 6 7 4 x 2 50 70 110 120 175 62 87, 5 84 77 83 65 120 88 89 83
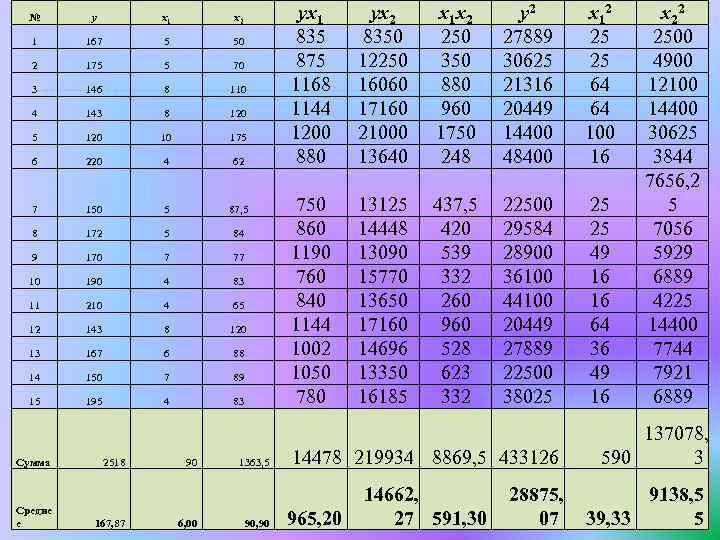
№ y x 1 x 2 1 167 5 50 2 175 5 70 3 146 8 110 4 143 8 120 5 120 10 175 6 220 4 62 7 150 5 87, 5 8 172 5 84 9 170 7 77 10 190 4 83 11 210 4 65 12 143 8 120 13 167 6 88 14 150 7 89 15 195 4 83 Сумма Средне е 2518 167, 87 90 6, 00 yx 1 835 875 1168 1144 1200 880 yx 2 8350 12250 16060 17160 21000 13640 x 1 x 2 250 350 880 960 1750 248 y 2 27889 30625 21316 20449 14400 48400 x 12 25 25 64 64 100 16 750 860 1190 760 840 1144 1002 1050 780 13125 14448 13090 15770 13650 17160 14696 13350 16185 437, 5 420 539 332 260 960 528 623 332 22500 29584 28900 36100 44100 20449 27889 22500 38025 25 25 49 16 16 64 36 49 16 1363, 5 14478 219934 8869, 5 433126 90, 90 14662, 27 591, 30 965, 20 28875, 07 x 22 2500 4900 12100 14400 30625 3844 7656, 2 5 7056 5929 6889 4225 14400 7744 7921 6889 137078, 590 3 9138, 5 39, 33 5

Find the average square deflections: Найдем средние квадратические отклонения переменных:

Find the coefficients of two variables correlation: Найдем коэффициенты парной корреляции:

Стандартизированные β-коэффициенты определим по формулам

Таким образом, уравнение регрессии в стандартизированной форме имеет вид: . Вывод: Сравнение модулей значений стандартизированных коэффициентов регрессии () говорит о том, что на цену автомобиля возраст (фактор х1) оказывает значительно большее влияние, нежели пробег (фактор х2). Рассчитаем естественные коэффициенты регрессии: Получаем уравнение линейной множественной (двухфакторной) регрессии в естественной форме: . Вывод: с увеличением возраста машины на 1 год ее цена уменьшается в среднем на 11, 56 тыс. рублей, а с увеличением пробега на 1 тыс. км цена уменьшается в среднем на 0, 08 тыс. рублей (80 рублей).

Find the coefficients of multiple correlation

Conclusion , Вывод: коэффициенты частной корреляции характеризуют тесноту связи между двумя переменными, исключив влияние третьей переменной. Значит, связь между ценой на автомобиль и годом выпуска при исключении влияния величины пробега обратная и заметная; между ценой автомобиля и пробегом без учета возраста машины – обратная, но слабая; связь между факторами x 1 и x 2 – умеренная. Сравним соответствующие коэффициенты парной и частной корреляции:
Multiple variables regression.ppt