Multiple Sequence Alignment Dynamic Programming Multiple Sequence

Multiple Sequence Alignment Dynamic Programming

Multiple Sequence Alignment VTISCTGSSSNIGAG NHVKWYQQLPG VTISCTGTSSNIGS ITVNWYQQLPG LRLSCSSSGFIFSS YAMYWVRQAPG LSLTCTVSGTSFDD YYSTWVRQPPG PEVTCVVVDVSHEDPQVKFNWYVDG ATLVCLISDFYPGA VTVAWKADS AALGCLVKDYFPEP VTVSWNSG- VSLTCLVKGFYPSD IAVEWESNG- • Goal: Bring the greatest number of similar characters into the same column of the alignment • Similar to alignment of two sequences.

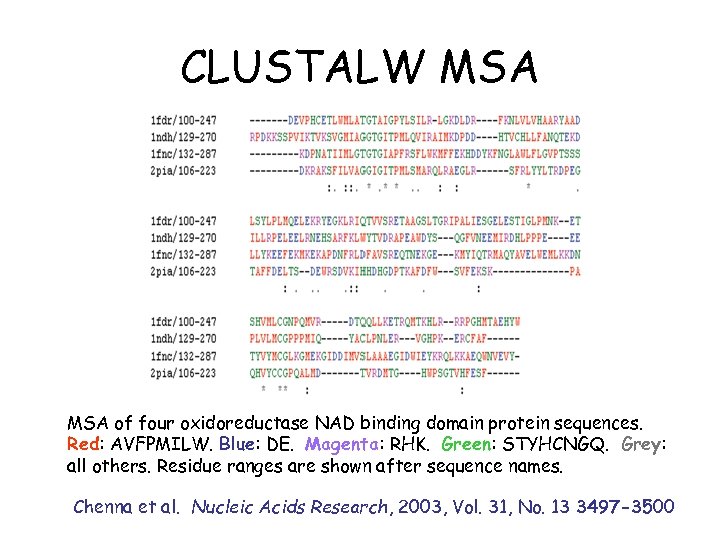CLUSTALW MSA of four oxidoreductase NAD binding domain protein sequences. Red: AVFPMILW. Blue: DE. Magenta: RHK. Green: STYHCNGQ. Grey: all others. Residue ranges are shown after sequence names. Chenna et al. Nucleic Acids Research, 2003, Vol. 31, No. 13 3497 -3500

Multiple Sequence Alignment: Motivation • Correspondence. Find out which parts “do the same thing” – Similar genes are conserved across widely divergent species, often performing similar functions • Structure prediction – Use knowledge of structure of one or more members of a protein MSA to predict structure of other members – Structure is more conserved than sequence • Create “profiles” for protein families – Allow us to search for other members of the family • Genome assembly: Automated reconstruction of “contig” maps of genomic fragments such as ESTs • MSA is the starting point for phylogenetic analysis

Multiple Sequence Alignment: Approaches • Optimal Global Alignments -Dynamic programming – Generalization of Needleman-Wunsch – Find alignment that maximizes a score function – Computationally expensive: Time grows as product of sequence lengths • Global Progressive Alignments - Match closelyrelated sequences first using a guide tree • Global Iterative Alignments - Multiple re-building attempts to find best alignment • Local alignments – Profiles, Blocks, Patterns

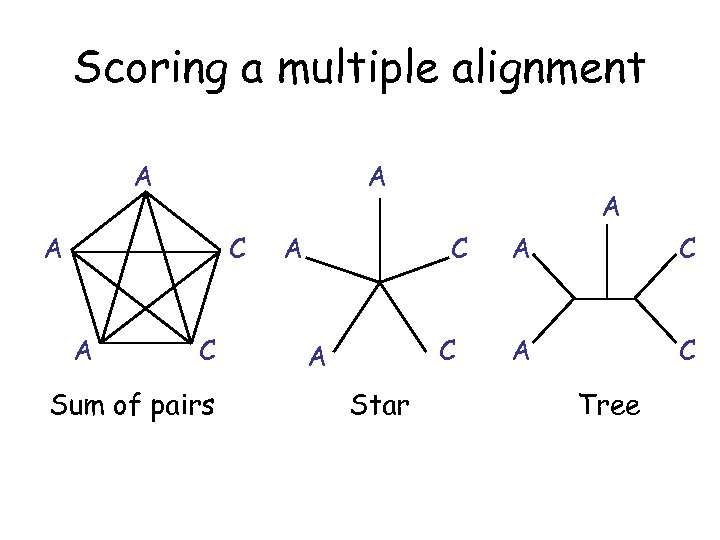Scoring a multiple alignment A A A C Sum of pairs A A C C A Star A C Tree

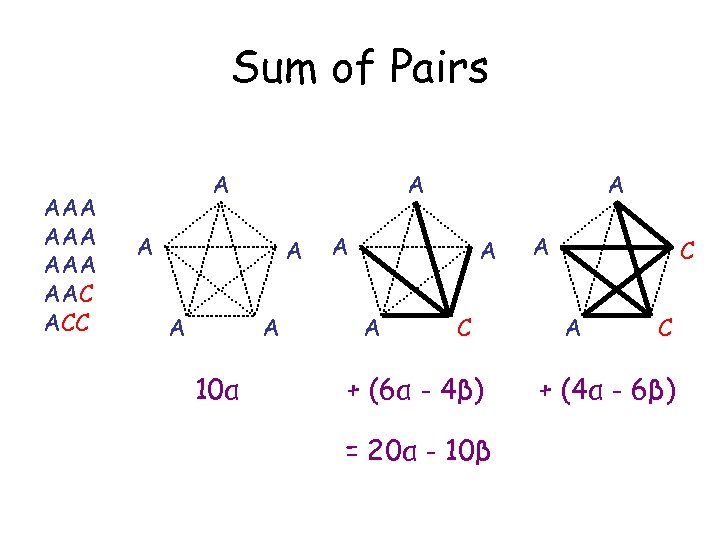Sum of Pairs AAA AAA AAC ACC A A A 10α A A C + (6α - 4β) = 20α - 10β A C + (4α - 6β)

Sum-of-Pairs Scoring Function Score of multiple alignment = ∑i

Induced Pairwise Alignment S 1 S 2 S 3 S - T I S C T G - S - N I L - T I – C N G S S - N I L R T I S C S G F S Q N I Induced pairwise alignment of S 1, S 2: S 1 S 2 S T I S C T G - S N I L T I – C N G S S N I

MSA: Dynamic Programming • The two-sequence alignment algorithm can be generalized to any number of sequences. • E. g. , for three sequences X, Y, W define C[i, j, k] = score of optimum alignment among X[1. . i], Y[1. . j], W[1. . k] • As for two sequences, divide possible alignments into different classes, depending on how they end. – Use to devise recurrence relations for C[i, j, k] – C[i, j, k] is the maximum out of all possibilities

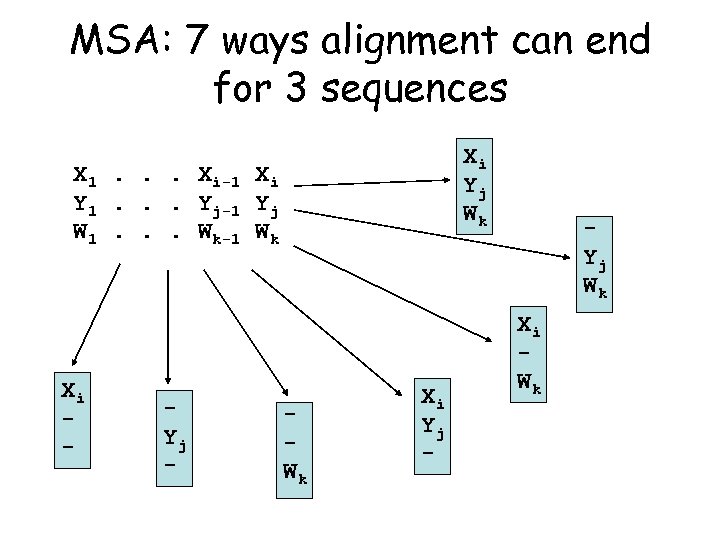MSA: 7 ways alignment can end for 3 sequences Xi Yj Wk X 1. . . Xi-1 Xi Y 1. . . Yj-1 Yj W 1. . . Wk-1 Wk Xi - Yj - Wk Xi Yj - Yj Wk Xi Wk

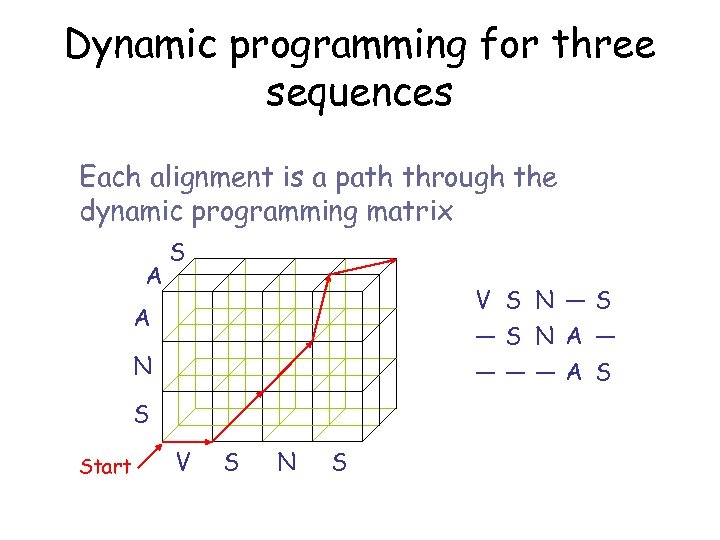Dynamic programming for three sequences Each alignment is a path through the dynamic programming matrix A S V S N —S —S N A — ———A S A N S Start V S N S

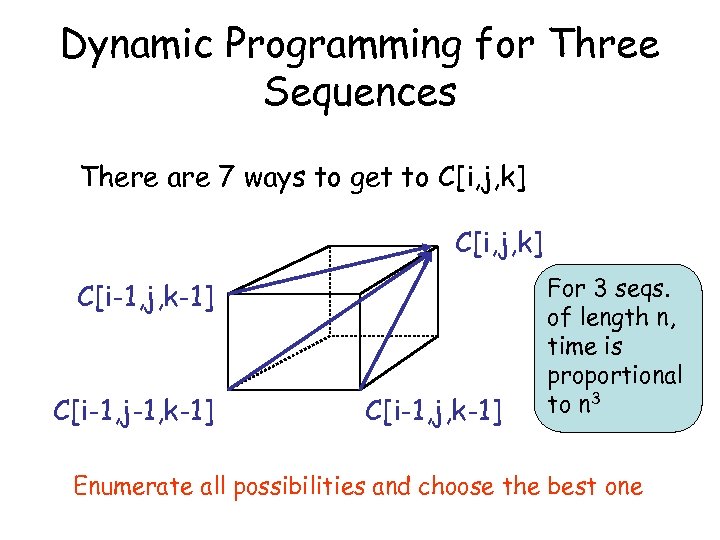Dynamic Programming for Three Sequences There are 7 ways to get to C[i, j, k] C[i-1, j, k-1] C[i-1, j-1, k-1] C[i-1, j, k-1] For 3 seqs. of length n, time is proportional to n 3 Enumerate all possibilities and choose the best one

Dynamic Programming MSA: General Case • For k sequences of length n, dynamic programming algorithm does (2 k-1) nk operations – Example: 6 sequences of length 100 require 6. 4 X 1013 calculations • Space for table is nk • Implementations (e. g. , Wash. U MSA 2. 1) use tricks and only search subset of dynamic programming table – Even this is expensive. E. g. , Baylor CM Search launcher limits MSA to 8 sequences of 800 characters and 10 minutes processing time

Problems with SP scoring • Pair-wise comparisons can over-score evolutionarily distant pairs. • Reason: For 3 or more sequences, SP scoring does not correspond to any evolutionary tree But not:

Overcoming problems with SP scoring • Use weights to incorporate evolution in sum of pairs scoring: – Some pair-wise alignments are more important than others • E. g. , more important to have a good alignment between mouse and human sequences than mouse and bird – Assign different weights to different pair-wise alignments. • Weight decreases with evolutionary distance. • Use star tree approach – one sequence is assigned as the ancestor and all others are contrasted it.

Star Alignments • Construct multiple alignments using pair-wise alignment relative to a fixed sequence • Out of a set S = {S 1, S 2, . . . , Sr} of sequences, pick sequence Sc that maximizes star_score(c) = ∑ {sim(Sc, Si) : 1 ≤ i ≤ r, i ≠ c} where sim(Si, Sj) is the optimal score of a pair-wise alignment between Si and Sj

Algorithm 1. Compute sim(Si, Sj) for every pair (i, j) 2. Compute star_score(i) for every i 3. Choose the index c that minimizes star_score(c) and make it the center of the star 4. Produce a multiple alignment M such that, for every i, the induced pairwise alignment of Sc and Si is the same as the optimum alignment of Sc and Si.

Step 4: Detail Sc AA--CCTT Sc A-ACC-TT S 1 AATGCC-- S 2 AGACCGT- Sc A-A--CC-TT S 1 A-ATGCC--- S 2 AGA--CCGT-