Multiple Regression 6 Sociology 5811 Lecture 27 Copyright

Multiple Regression 6 Sociology 5811 Lecture 27 Copyright © 2005 by Evan Schofer Do not copy or distribute without permission

Announcements • Final paper due now!!! • Course Evaluations • Wrap up multiple regression • Discuss issues of causality, if time remains.

Review: Outliers • Strategy for identifying outliers: • 1. Look at scatterplots or regression partial plots for extreme values • Easiest. A minimum for final projects • 2. Ask SPSS to compute outlier diagnostic statistics – Examples: “Leverage”, Cook’s D, DFBETA, residuals, standardized residuals.

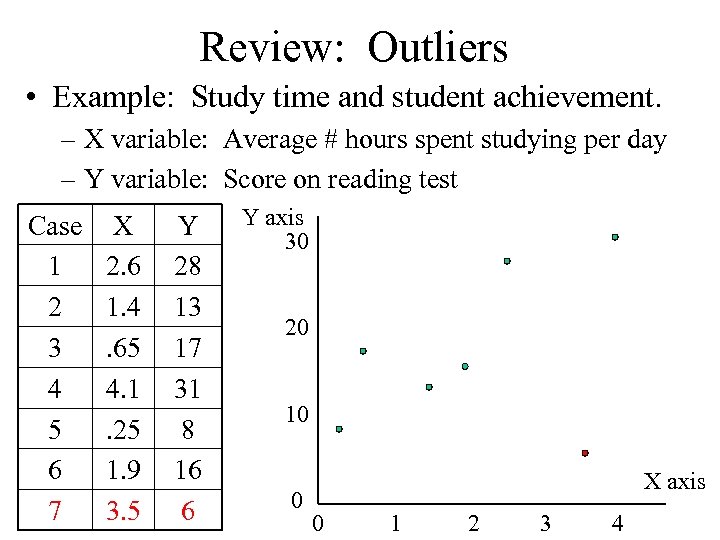Review: Outliers • Example: Study time and student achievement. – X variable: Average # hours spent studying per day – Y variable: Score on reading test Case 1 2 3 4 5 6 7 X 2. 6 1. 4. 65 4. 1. 25 1. 9 3. 5 Y 28 13 17 31 8 16 6 Y axis 30 20 10 0 X axis 0 1 2 3 4

Review: Outliers • Cook’s D: Identifies cases that are strongly influencing the regression line – SPSS calculates a value for each case • Go to “Save” menu, click on Cook’s D • How large of a Cook’s D is a problem? – Rule of thumb: Values greater than: 4 / (n – k – 1) – Example: N=7, K = 1: Cut-off = 4/5 =. 80 – Cases with higher values should be examined • Big residuals also can indicate outliers.

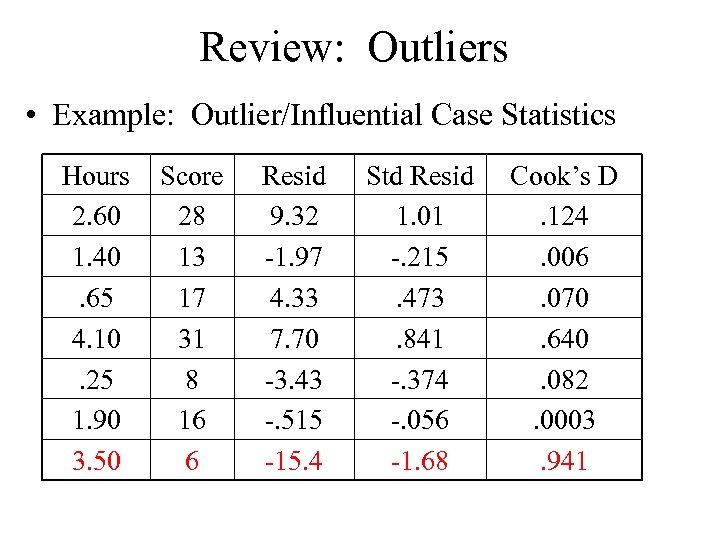Review: Outliers • Example: Outlier/Influential Case Statistics Hours 2. 60 1. 40. 65 4. 10. 25 1. 90 3. 50 Score 28 13 17 31 8 16 6 Resid 9. 32 -1. 97 4. 33 7. 70 -3. 43 -. 515 -15. 4 Std Resid 1. 01 -. 215. 473. 841 -. 374 -. 056 -1. 68 Cook’s D. 124. 006. 070. 640. 082. 0003. 941

Review: Outliers • Question: Should you drop “outlier” cases? – Obviously, you should drop cases that are incorrectly coded or erroneous – But, you should be cautious about throwing out cases • If you throw out enough cases, you can produce any result that you want! So, be judicious when destroying data • When in doubt: Present results both with and without outliers – Or present one set of results, but mention how results differ depending on how outliers were handled.

Multicollinearity • Another common regression problem: Multicollinearity • Definition: collinear = highly correlated – Multicollinearity = inclusion of highly correlated independent variables in a single regression model • Recall: High correlation of X variables causes problems for estimation of slopes (b’s) – Recall: variable denominators approach zero, coefficients may wrong/too large.

Multicollinearity • Multicollinearity symptoms: • Unusually large standard errors and betas • Compared to if both collinear variables aren’t included • Betas often exceed 1. 0 • Two variables have the same large effect when included separately… but… – When put together the effects of both variables shrink – Or, one remains positive and the other flips sign • Note: Not all “sign flips” are due to multicollinearity!

Multicollinearity • What does multicollinearity do to models? – Note: It does not violate regression assumptions • But, it can mess things up anyway • 1. Multicollinearity can inflate standard error estimates – Large standard errors = small t-values = no rejected null hypotheses – Note: Only collinear variables are effected. The rest of the model results are OK.

Multicollinearity • What does multicollinearity do? • 2. It leads to instability of coefficient estimates – Variable coefficients may fluctuate wildly when a collinear variable is added – These fluctuations may not be “real”, but may just reflect amplification of “noise” and “error” • One variable may only be slightly better at predicting Y… but SPSS will give it a MUCH higher coefficient – Note: These only affect variables that are highly correlated. The rest of the model is OK.

Multicollinearity • Diagnosing multicollinearity: • 1. Look at correlations of all independent vars – Correlation of. 7 is a concern, . 8> is often a problem – But, sometimes problems aren’t always bivariate… and don’t show up in bivariate correlations • Ex: If you forget to omit a dummy variable • 2. Watch out for the “symptoms” • 3. Compute diagnostic statistics • Tolerances, VIF (Variance Inflation Factor).

Multicollinearity • Multicollinearity diagnostic statistics: • “Tolerance”: Easily computed in SPSS – Low values indicate possible multicollinearity • Start to pay attention at. 4; Below. 2 is very likely to be a problem – Tolerance is computed for each independent variable by regressing it on other independent variables.

Multicollinearity • If you have 3 independent variables: X 1, X 2, X 3… – Tolerance is based on doing a regression: X 1 is dependent; X 2 and X 3 are independent. • Tolerance for X 1 is simply 1 minus regression R-square. • If a variable (X 1) is highly correlated with all the others (X 2, X 3) then they will do a good job of predicting it in a regression • Result: Regression r-square will be high… 1 minus rsquare will be low… indicating a problem.

Multicollinearity • Variance Inflation Factor (VIF) is the reciprocal of tolerance: 1/tolerance • High VIF indicates multicollinearity – Gives an indication of how much the Standard Error of a variable grows due to presence of other variables.

Multicollinearity • Solutions to multcollinearity – It can be difficult if a fully specified model requires several collinear variables • 1. Drop unnecessary variables • 2. If two collinear variables are really measuring the same thing, drop one or make an index – Example: Attitudes toward recycling; attitude toward pollution. Perhaps they reflect “environmental views” • 3. Advanced techniques: e. g. , Ridge regression • Uses a more efficient estimator (but not BLUE – may introduce bias).

Nested Models • It is common to conduct a series of multiple regressions – Adding new variables or sets of variables to a model • Example: Student achievement in school • Suppose you are interested in effects of neighborhood – You might first look at all demographic effects… – Then add neighborhood variables as a group • Hopefully to show that they improve the model.

Nested Models • Question: Do the new variables substantially improve the model? • Idea #1: See if your variables are significant • Idea #2: See if there is an increase in the adjusted R-Square • Idea #3: Conduct an F-test – A formal test to see if the group of variables improves the model as a whole (increases the R-square) – Recall that F-tests allow comparisons of variance (e. g. , SSbetween to SSwithin).

Nested Models • F-tests require “nested models” – Models are the same, except for addition of new variables – You can’t compare totally different models this way • Tests following Hypotheses: • H 0: Two models have the same R-square • H 1: Two models have different R-square

Nested Models • SPSS can conduct an F-test between two regression models • A significant F-test indicates: • The second model (with additional variables) is a significant improvement (in R-square) compared to the first.

Extensions of Regression • The multivariate regression model has been altered and extended in many ways – Many techniques are “regression analogues” – Often, they address shortcomings of regression • Problem: Regression requires that the dependent variable is interval • Solution: Logistic Regression (also Probit, others) – Allows analysis dichotomous dependent variable

Extensions of Regression • Problem: Many variables are “counts” – Example: Number of crimes committed – Counts = non-negative integers; often highly skewed • Solution: Poisson Regression and Negative Binomial Regression – These models use a non-linear approach to model counts.

Extensions of Regression • Problem: Sometimes we want to measure cases at multiple points in time – Example: economic data for companies – Cases are not independent, errors may be correlated • Solution: Time-series procedures: – ARIMA; Prais-Winston; Newey West, and others – All different ways to address serial correlation of errors.

Extensions of Regression • Problem: Sometimes cases are not independent because they are part of larger groups – Example: Research on students in several schools – Cases within each school share certain similarities (e. g. , neighborhood). They are not independent. • Solution: Hierarchical Linear Models (HLM).

Extensions of Regression • Problem: Severe measurement error • Solution: Structural equation models with latent variables • Uses multiple indicators to estimate a better model • Problem: Sample selection issues • Solution: Heckman sample selection model • AND: there are many more… • Event history analysis • Fixed and random effects models for pooled time series • Etc. etc. , etc…

Models and “Causality” • Issue: People often use statistics to support theories or claims regarding causality – They hope to “explain” some phenomena • What factors make kids drop out of school • Whether or not discrimination leads to wage differences • What factors make corporations earn higher profits • Statistics provide information about association • Always remember: Association (e. g. , correlation) is not causation! • The old aphorism is absolutely right • Association can always be spurious

Models and “Causality” • How do we determine causality? • The randomized experiment is held up as the ideal way to determine causality • Example: Does drug X cure cancer? • We could look for association between receiving drug X and cancer survival in a sample of people • But: Association does not demonstrate causation; Effect could be spurious • Example: Perhaps rich people have better access to drug X; and rich people have more skilled doctors! • Can you think of other possible spurious processes?

Models and “Causality” • In a randomized experiment, people are assigned randomly to take drug X (or not) • Thus, taking drug X is totally random and totally uncorrelated with any other factor (such as wealth, gender, access to high quality doctors, etc) • As a result, the association between drug X and cancer survival cannot be affected by any spurious factor • Nor can “reverse causality” be a problem • SO: We can make strong inferences about causality!

Models and “Causality” • Unfortunately, randomized experiments are impractical (or unethical) in many cases • Example: Consequences of high-school dropout, national democracy, or impact of homelessness • Plan B: Try to “control” for spurious effects: • Option 1: Create homogenous sub-groups – Effects of Drug X: If there is a spurious relationship with wealth, compare people with comparable wealth • Ex: Look at effect of drug X on cancer survivors among people of constant wealth… eliminating spurious effect.

Models and “Causality” • Option 2: Use multivariate model to “control” for spurious effects • Examine effect of key variable “net” of other relationships – Ex: Look at effect of Drug X, while also including a variable for wealth • Result: Coefficients for Drug X represent effect net of wealth, avoiding spuriousness.

Models and “Causality” • Limitations of “controls” to address spuriousness • 1. The “homogenous sub-groups” reduces N • To control for many possible spurious effects, you’ll throw away lots of data • 2. You have to control for all possible spurious effects • If you overlook any important variable, your results could be biased… leading to incorrect conclusions about causality • First: It is hard to measure and control for everything • Second: Someone can always think up another thing you should have controlled for, undermining your causal claims.

Models and “Causality” • Under what conditions can a multivariate model support statements about causality? • In theory: A multivariate model support claims about causality… IF: • The sample is unbiased • The measurement is accurate • The model includes controls for every major possible spurious effect • The possibility of reverse causality can be ruled out • And, the model is executed well: assumptions, outliers, multicollinearity, etc. are all OK.

Models and “Causality” • In Practice: Scholars commonly make tentative assertions about causality… IF: • The data set is of high quality; sample is either random or arguably not seriously biased • Measures are high quality by the standards of the literature • The model includes controls for major possible spurious effects discussed in the prior literature • The possibility of reverse causality is arguably unlikely • And, the model is executed well: assumptions, outliers, multicollinearity, etc. are all acceptable… (OR, the author uses variants of regression necessary to address problems).

Models and “Causality” • In sum: Multivariate analysis is not the ideal tool to determine causality • If you can run an experiment, do it • But: Multivariate models are usually the best tool that we have! • Advice: Multivariate models are a terrific way to explore your data • Don’t forget: “correlation is not causation” • The models aren’t magic; they simply sort out correlation • But, if used thoughtfully, they can provide hints into likely causal processes!