Скачать презентацию Мультимедийные лекции по физике Магнетизм Тема 3. Скачать презентацию Мультимедийные лекции по физике Магнетизм Тема 3.

Эл. лек. Магнетизм 3.ppt

  • Количество слайдов: 61

Мультимедийные лекции по физике Магнетизм Мультимедийные лекции по физике Магнетизм

Тема 3. Силы магнитного поля План лекции 3. 1. Сила Ампера. 3. 2. Сила Тема 3. Силы магнитного поля План лекции 3. 1. Сила Ампера. 3. 2. Сила взаимодействия параллельных токов. 3. 3. Сила Лоренца. 3. 4. Движение заряженных частиц в магнитном поле. 3. 5. Ускорители заряженных частиц. 3. 6. Работа сил магнитного поля.

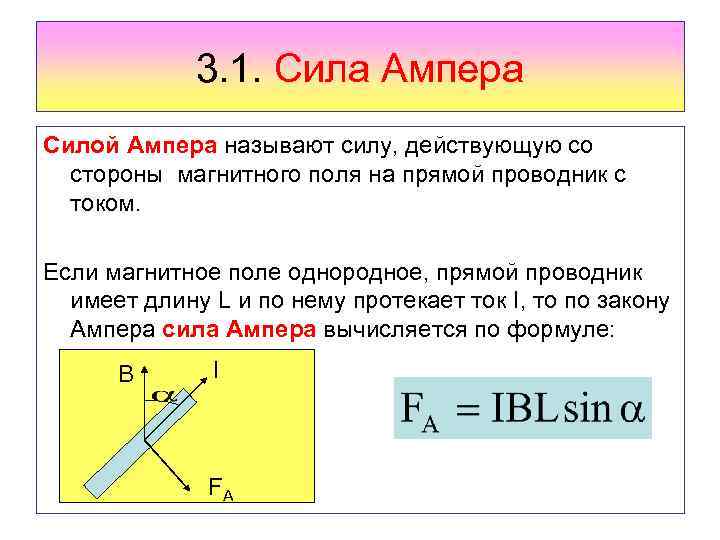3. 1. Сила Ампера Силой Ампера называют силу, действующую со стороны магнитного поля на 3. 1. Сила Ампера Силой Ампера называют силу, действующую со стороны магнитного поля на прямой проводник с током. Если магнитное поле однородное, прямой проводник имеет длину L и по нему протекает ток I, то по закону Ампера сила Ампера вычисляется по формуле: В I FA

Сила Ампера Сила Ампера

Сила Ампера, действующая на элемент тока , запишется как - угол между направлением Сила Ампера, действующая на элемент тока , запишется как - угол между направлением силы тока в проводнике и вектором магнитной индукции. Если этот угол равен 90 О, то направление силы Ампера определяется по правилу левой руки.

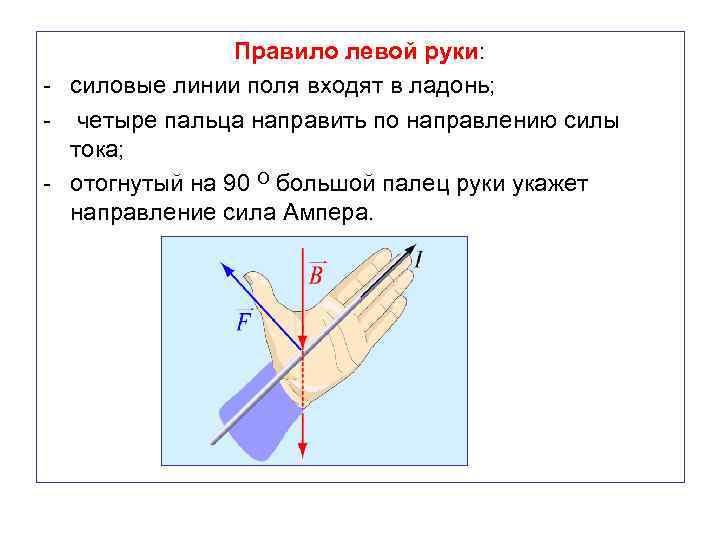Правило левой руки: - силовые линии поля входят в ладонь; - четыре пальца направить Правило левой руки: - силовые линии поля входят в ладонь; - четыре пальца направить по направлению силы тока; - отогнутый на 90 О большой палец руки укажет направление сила Ампера.

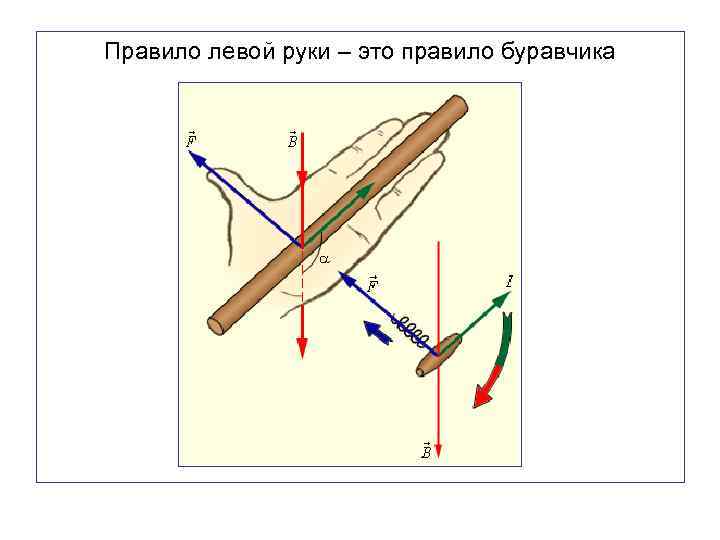Правило левой руки – это правило буравчика Правило левой руки – это правило буравчика

Второе определение магнитной индукции: магнитная индукция равна максимальной силе Ампера, действующей на проводник единичной Второе определение магнитной индукции: магнитная индукция равна максимальной силе Ампера, действующей на проводник единичной длины с единичной силой тока.

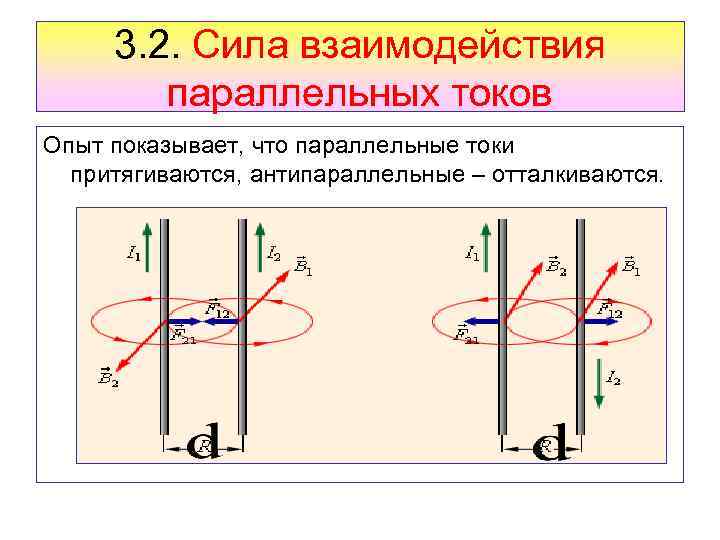3. 2. Сила взаимодействия параллельных токов Опыт показывает, что параллельные токи притягиваются, антипараллельные – 3. 2. Сила взаимодействия параллельных токов Опыт показывает, что параллельные токи притягиваются, антипараллельные – отталкиваются.

Иллюстрация магнитных сил притяжения и отталкивания Иллюстрация магнитных сил притяжения и отталкивания

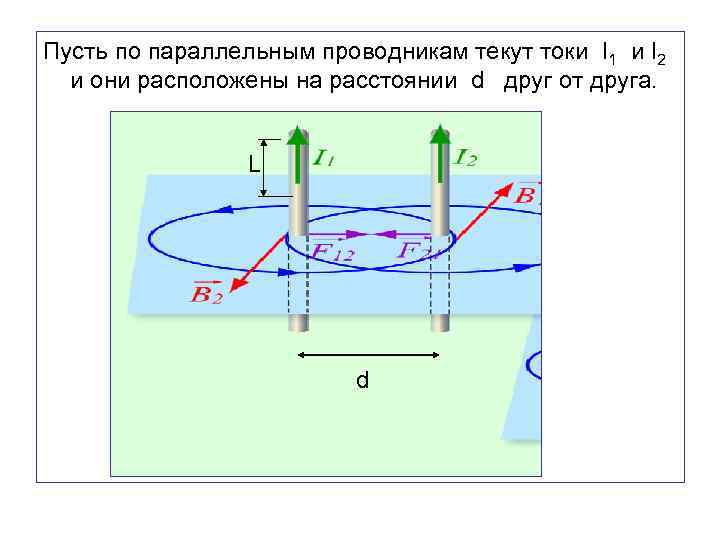Пусть по параллельным проводникам текут токи I 1 и I 2 и они расположены Пусть по параллельным проводникам текут токи I 1 и I 2 и они расположены на расстоянии d друг от друга. L d

Будем считать, что ток I 1 создаёт магнитное поле. Тогда на расстоянии d от Будем считать, что ток I 1 создаёт магнитное поле. Тогда на расстоянии d от проводника вектор магнитной индукции направлен от нас по касательной к силовой линии, направление которой определяется правилом буравчика. Модуль вектора : Магнитное поле первого тока действует на второй ток с силой Ампера:

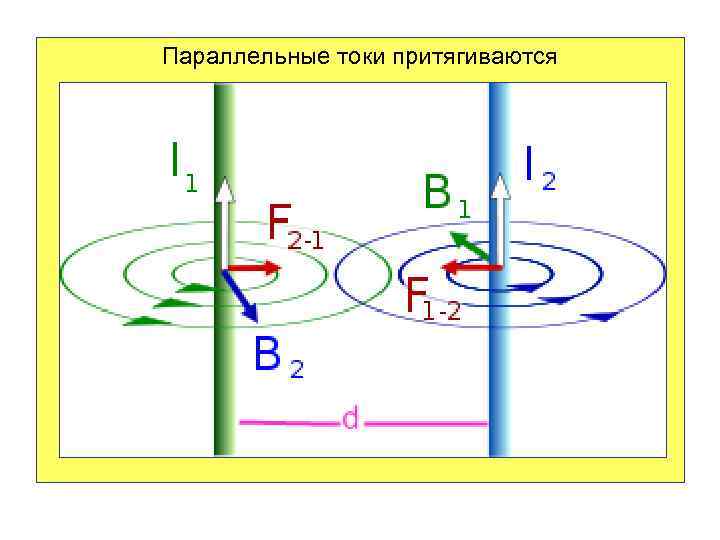Параллельные токи притягиваются Параллельные токи притягиваются

Совместная подстановка формул определяет закон взаимодействия параллельных токов: L – длина взаимодействующих частей проводников. Совместная подстановка формул определяет закон взаимодействия параллельных токов: L – длина взаимодействующих частей проводников. Формулировка закона: Сила взаимодействия параллельных токов прямо пропорциональна произведению силы токов в проводниках, длине проводников и обратно пропорциональна расстоянию между ними.

Из формулы следуют два понятия. 1. 1 ампер – сила такого постоянного тока, который, Из формулы следуют два понятия. 1. 1 ампер – сила такого постоянного тока, который, проходя по двум бесконечно длинным проводникам малого сечения, расположенным в вакууме на расстоянии 1 м, создаёт силу взаимодействия, равную 2 10 -7 Н на каждый метр длины проводника. 2. Величина магнитной постоянной:

3. 3. Сила Лоренца Магнитное поле на элемент тока действует с силой Ампера. Ток 3. 3. Сила Лоренца Магнитное поле на элемент тока действует с силой Ампера. Ток – направленное движение зарядов. Значит магнитное поле действует на каждый отдельный заряд. Эту силу, имеющей название силы Лоренца, можно определить, поделив силу Ампера на количество зарядов в элементе тока: FЛ = FA/N.

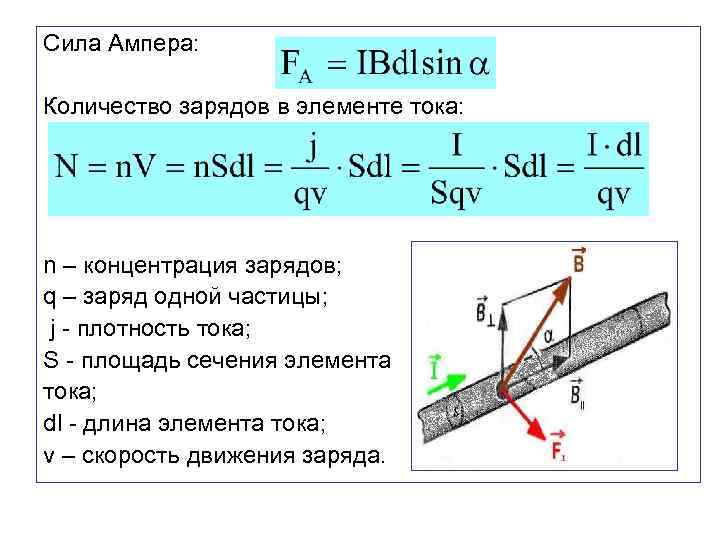Сила Ампера: Количество зарядов в элементе тока: n – концентрация зарядов; q – заряд Сила Ампера: Количество зарядов в элементе тока: n – концентрация зарядов; q – заряд одной частицы; j - плотность тока; S - площадь сечения элемента тока; dl - длина элемента тока; v – скорость движения заряда.

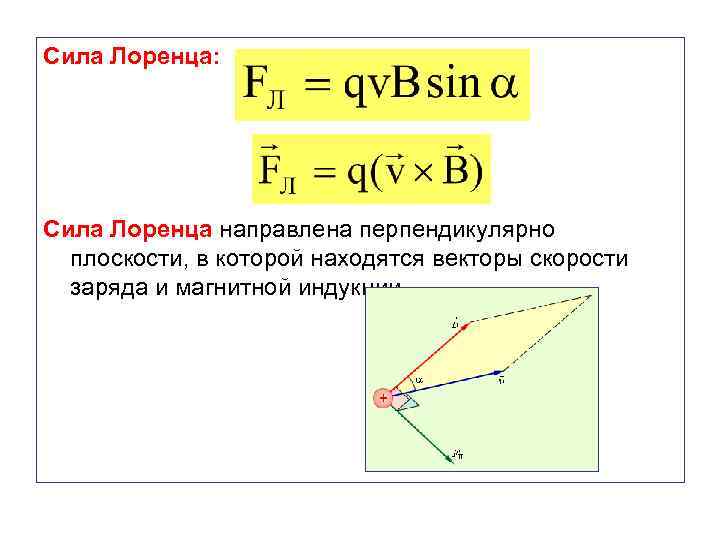Сила Лоренца: Сила Лоренца направлена перпендикулярно плоскости, в которой находятся векторы скорости заряда и Сила Лоренца: Сила Лоренца направлена перпендикулярно плоскости, в которой находятся векторы скорости заряда и магнитной индукции.

- угол между направлениями векторов скорости и магнитной индукции. Если угол , то - угол между направлениями векторов скорости и магнитной индукции. Если угол , то направление силы Лоренца определяют по правилу левой руки для положительно заряженных частиц. Правило левой руки: - магнитная индукция входит в ладонь; - четыре пальца направить по вектору скорости положительно заряженной частицы; - отогнутый на 90 О большой палец руки укажет направление силы Лоренца.

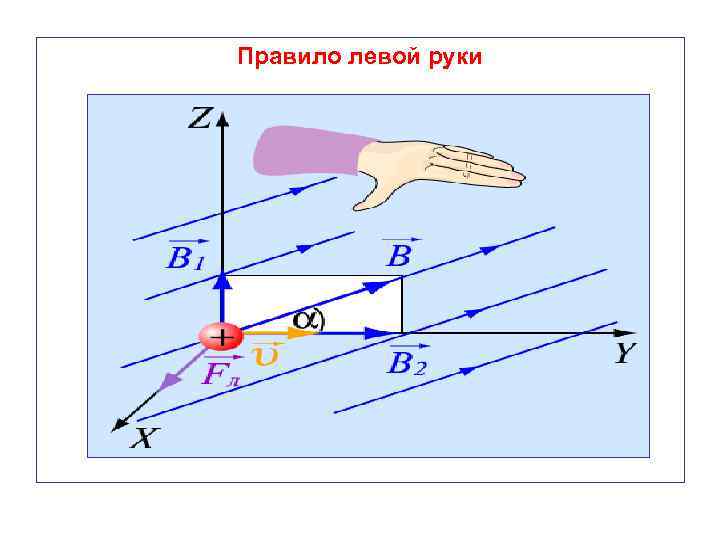Правило левой руки Правило левой руки

3. 4. Движение заряженных частиц в магнитном поле Траектория движения заряженных частиц в магнитном 3. 4. Движение заряженных частиц в магнитном поле Траектория движения заряженных частиц в магнитном поле будет зависеть от угла между направлением скорости движения частицы и направлением магнитной индукции. 1. Если , то сила Лоренца . Частица не испытывает действия магнитного поля и будет двигаться равномерно и прямолинейно вдоль силовых линий поля.

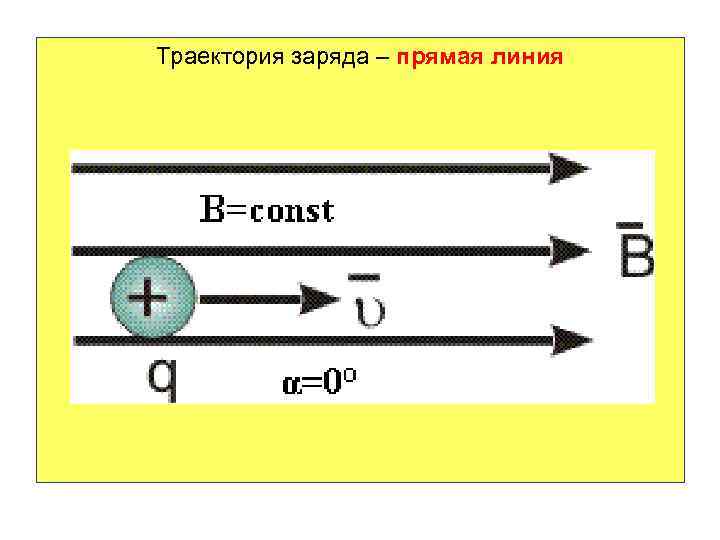Траектория заряда – прямая линия Траектория заряда – прямая линия

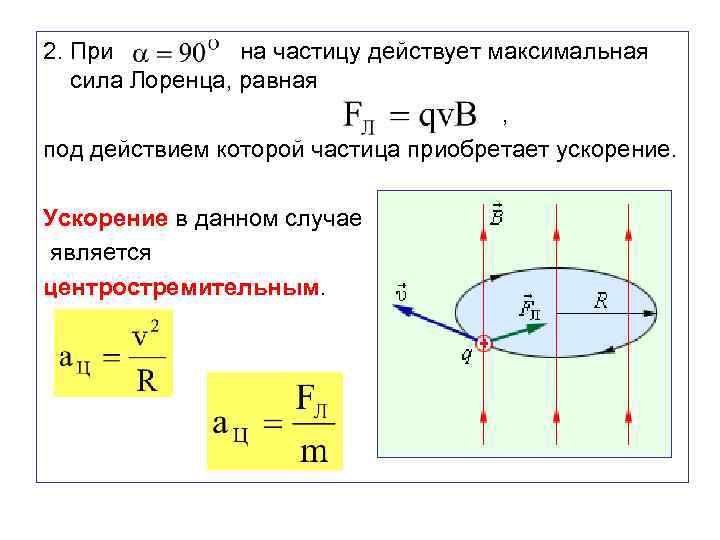2. При на частицу действует максимальная сила Лоренца, равная , под действием которой частица 2. При на частицу действует максимальная сила Лоренца, равная , под действием которой частица приобретает ускорение. Ускорение в данном случае является центростремительным.

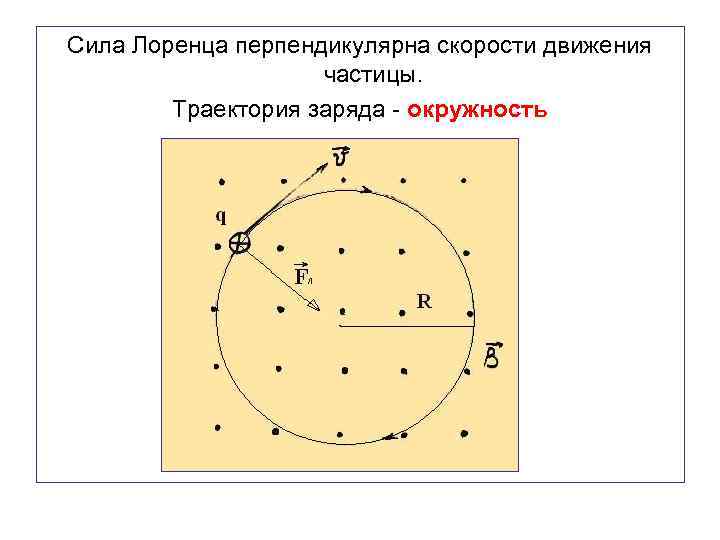Сила Лоренца перпендикулярна скорости движения частицы. Траектория заряда - окружность Сила Лоренца перпендикулярна скорости движения частицы. Траектория заряда - окружность

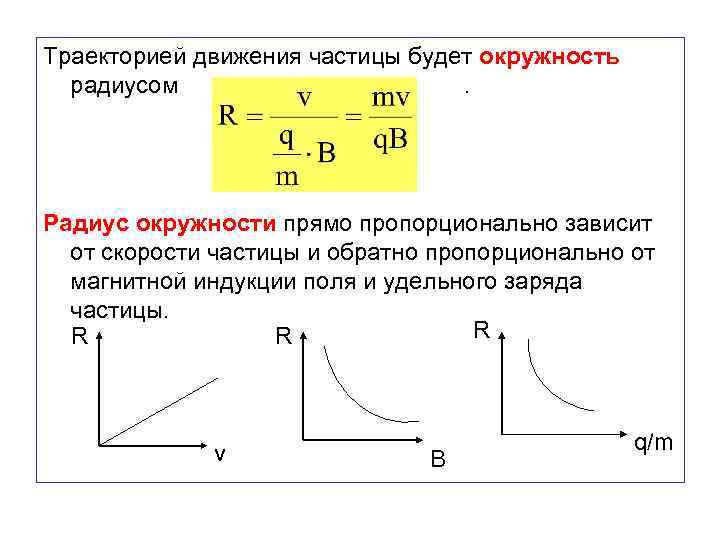Траекторией движения частицы будет окружность радиусом . Радиус окружности прямо пропорционально зависит от скорости Траекторией движения частицы будет окружность радиусом . Радиус окружности прямо пропорционально зависит от скорости частицы и обратно пропорционально от магнитной индукции поля и удельного заряда частицы. R R R v B q/m

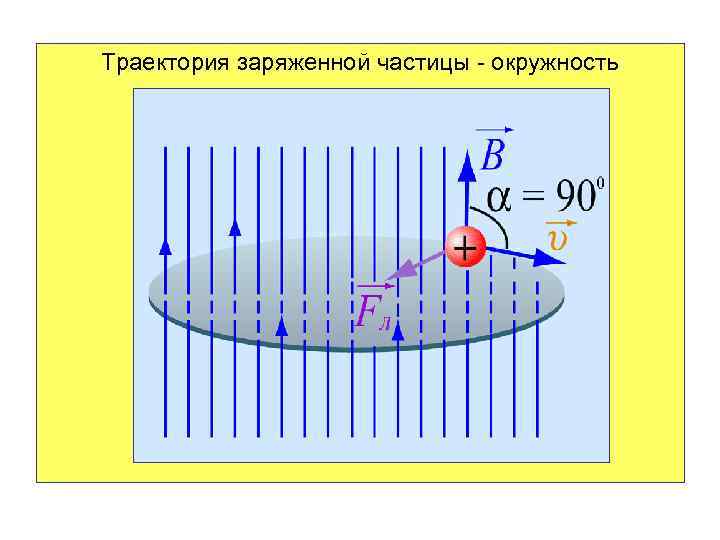Траектория заряженной частицы - окружность Траектория заряженной частицы - окружность

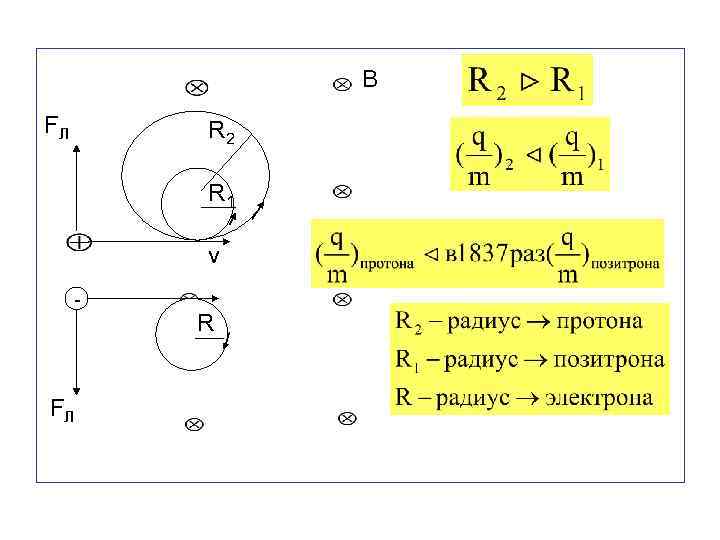
Правило левой руки для силы Лоренца Зависимость радиуса окружности от удельного заряда частицы позволяет Правило левой руки для силы Лоренца Зависимость радиуса окружности от удельного заряда частицы позволяет различить заряженные частицы друг от друга. Для этого поток частиц «впрыскивают» в перпендикулярное скорости частицы магнитное поле. Частицы с разным удельным зарядом, но одинаковые по знаку, будут двигаться по окружностям разного радиуса. Частицы противоположного знака заряда будут заворачиваться в разные стороны.

B FЛ R 2 R 1 v - R FЛ B FЛ R 2 R 1 v - R FЛ

Период и частота обращения по окружности не зависит от скорости движения частицы: Угловая скорость Период и частота обращения по окружности не зависит от скорости движения частицы: Угловая скорость движения заряженной частицы по круговой траектории называется циклотронной частотой. Независимость циклотронной частоты от скорости частицы используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов).

3. Если частица влетает в магнитное поле под любым углом , кроме 0 О 3. Если частица влетает в магнитное поле под любым углом , кроме 0 О и 90 О, то траекторией движения будет являться винтовая линия с шагом h и и радиусом R. В этом случае скорость раскладывают на две составляющие: параллельную направлению магнитной индукции и перпендикулярную к ней . v B=const

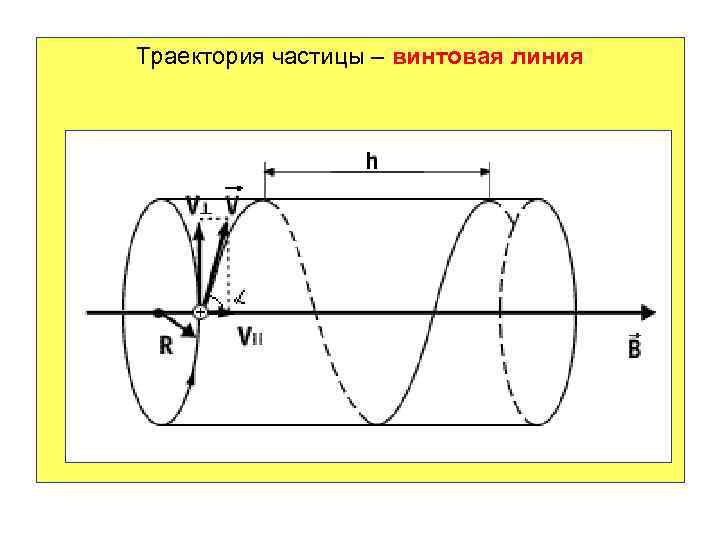Траектория частицы – винтовая линия Траектория частицы – винтовая линия

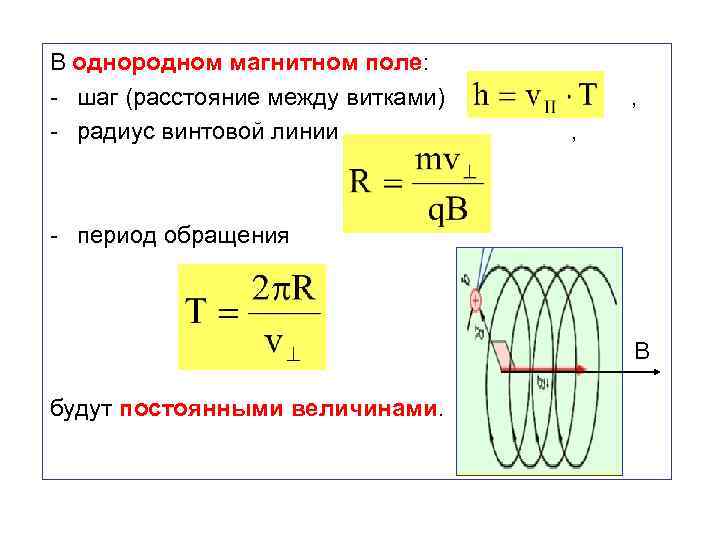В однородном магнитном поле: - шаг (расстояние между витками) , - радиус винтовой линии В однородном магнитном поле: - шаг (расстояние между витками) , - радиус винтовой линии , - период обращения В будут постоянными величинами.

В случае неоднородного поля винтовая линия будет видоизменяться. Если вдоль движения частицы магнитное поле В случае неоднородного поля винтовая линия будет видоизменяться. Если вдоль движения частицы магнитное поле будет возрастать, то: - радиус винтовой линии будет уменьшаться, - период будет уменьшаться, - шаг между витками также будет уменьшаться. В целом винтовая линия будет сжиматься. По такой траектории движутся частицы, летящие из космоса и попадающие в магнитное поле Земли.

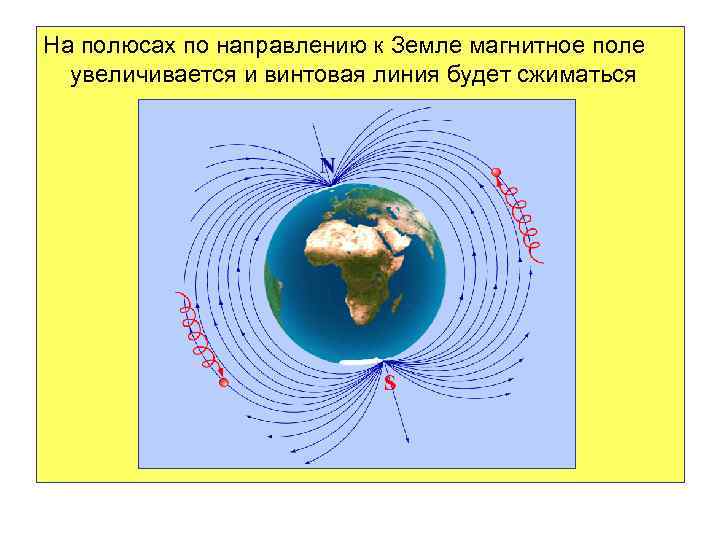На полюсах по направлению к Земле магнитное поле увеличивается и винтовая линия будет сжиматься На полюсах по направлению к Земле магнитное поле увеличивается и винтовая линия будет сжиматься

Движение заряженной частицы по винтовой линии, когда траектория частицы как бы навивается на линии Движение заряженной частицы по винтовой линии, когда траектория частицы как бы навивается на линии магнитной индукции используется в технике для магнитной термоизоляции высокотемпературной плазмы. Плазма - это полностью ионизированный газ при температуре порядка 106 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации.

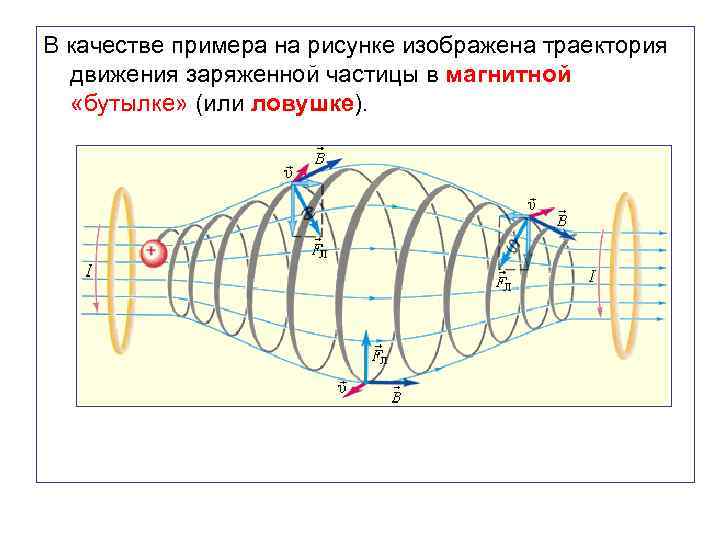В качестве примера на рисунке изображена траектория движения заряженной частицы в магнитной «бутылке» (или В качестве примера на рисунке изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке).

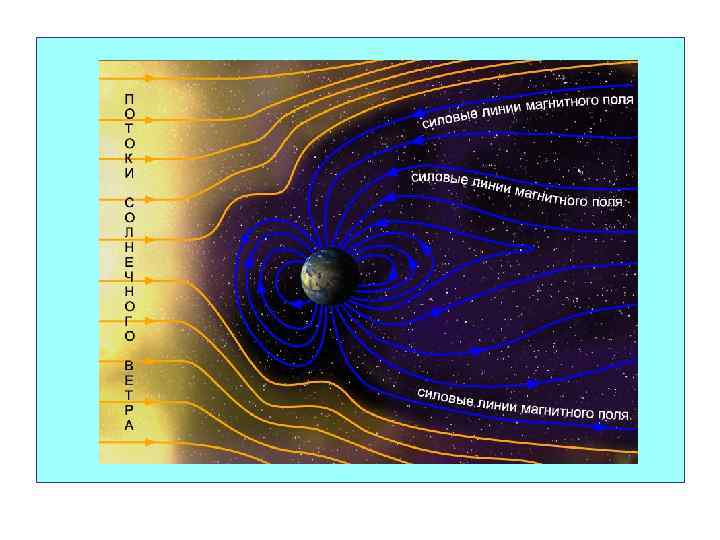
Магнитные ловушки наблюдаются и в магнитном поле Земли. Летящие из космоса быстрые заряженные частицы Магнитные ловушки наблюдаются и в магнитном поле Земли. Летящие из космоса быстрые заряженные частицы «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса. В радиационных поясах, как в магнитных ловушках, частицы перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды.

Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Магнитное поле Земли является защитой для всего живого от потоков заряженных частиц из космического пространства.

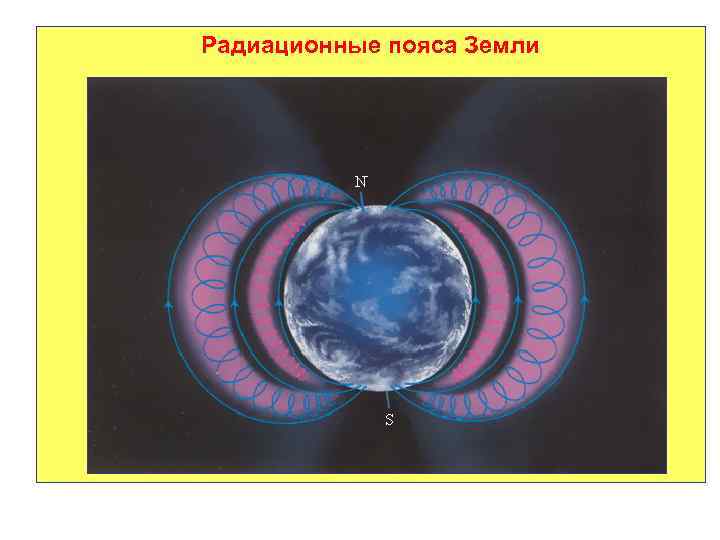Радиационные пояса Земли Радиационные пояса Земли

3. 5. Ускорители заряженных частиц: - устройства, в которых под действием электрических и магнитных 3. 5. Ускорители заряженных частиц: - устройства, в которых под действием электрических и магнитных полей создаются и управляются пучки заряженных частиц; Ускорители заряженных частиц характеризуются: - типом ускоряемых частиц: электронов, протонов, мезонов и др. ; - энергией, сообщаемой частицам: а именно «разбросом» частиц по энергиям и интенсивностью пучка.

Ускорители заряженных частиц делятся на: - непрерывные (из них выходит равномерный по времени поток Ускорители заряженных частиц делятся на: - непрерывные (из них выходит равномерный по времени поток частиц); - импульсные ( из н их частицы вылетают порциями – импульсами). Ускорители заряженных частиц по форме траектории и механизму ускорения частиц делятся на: - линейные; - циклические; - индукционные.

В линейных ускорителях траектории движения частиц близки к прямым линиям. В циклических и индукционных В линейных ускорителях траектории движения частиц близки к прямым линиям. В циклических и индукционных ускорителях – траекториями являются окружности или винтовые линии (спирали). Независимость циклотронной частоты от скорости частицы используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов).

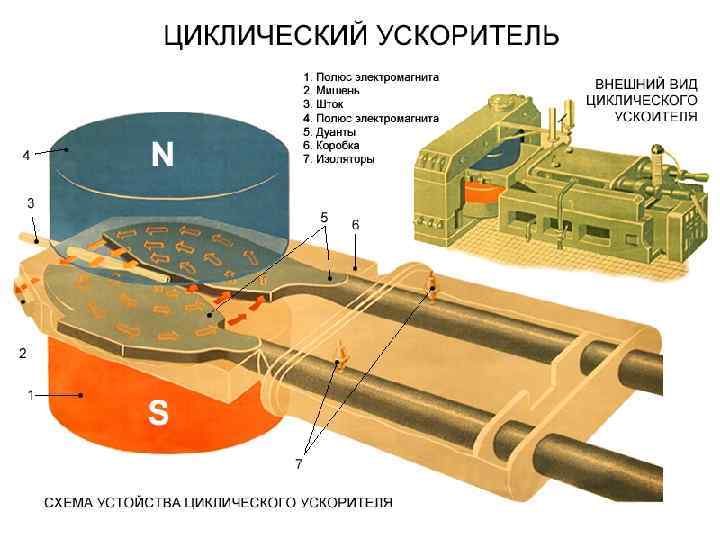
Циклотрон был разработан в 1932 г. Лоуренсом для ускорения протонов и ионов. Такие частицы Циклотрон был разработан в 1932 г. Лоуренсом для ускорения протонов и ионов. Такие частицы можно было использовать для столкновений с атомными ядрами. В результате была получена богатая информация об атомных ядрах и элементарных частицах. Циклотрон состоит из двух D-образных полых металлических электродов (дуантов), внутри которых на частицы действует магнитное поле, перпендикулярное их движению.

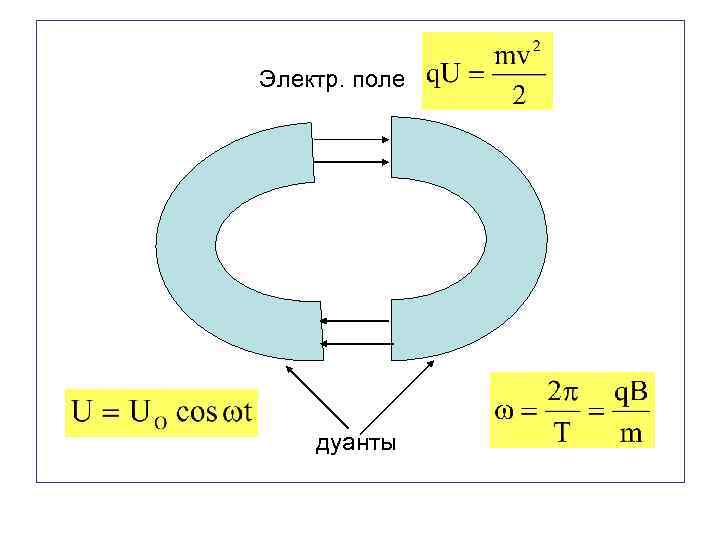Электр. поле дуанты Электр. поле дуанты

Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Всякий раз, когда частицы попадают в промежуток между дуантами (зазор), к электродам прикладывается ускоряющее электрическое напряжение. В свою очередь, ускоряющее напряжение приводит к увеличение скорости частиц, следовательно, радиуса их траектории.

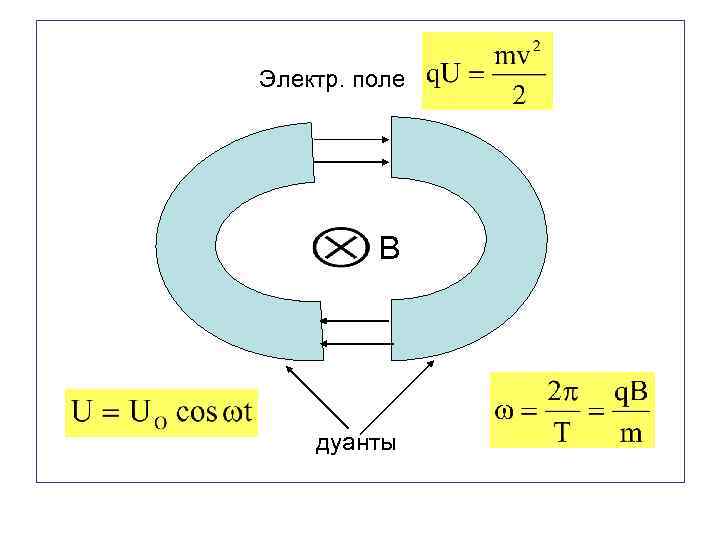Электр. поле В дуанты Электр. поле В дуанты

После большого числа оборотов частицы приобретают значительную кинетическую энергию и достигают периферии циклотрона. В После большого числа оборотов частицы приобретают значительную кинетическую энергию и достигают периферии циклотрона. В конце концов частицы попадают на мишень, установленную внутри циклотрона, или выводятся из циклотрона на внешнюю мишень. Приложенное к дуантам ускоряющее напряжение должно быть переменным. Частота приложенного напряжения должна быть равна циклотронной частоте вращения частиц, которая не зависит от радиуса круговой траектории.

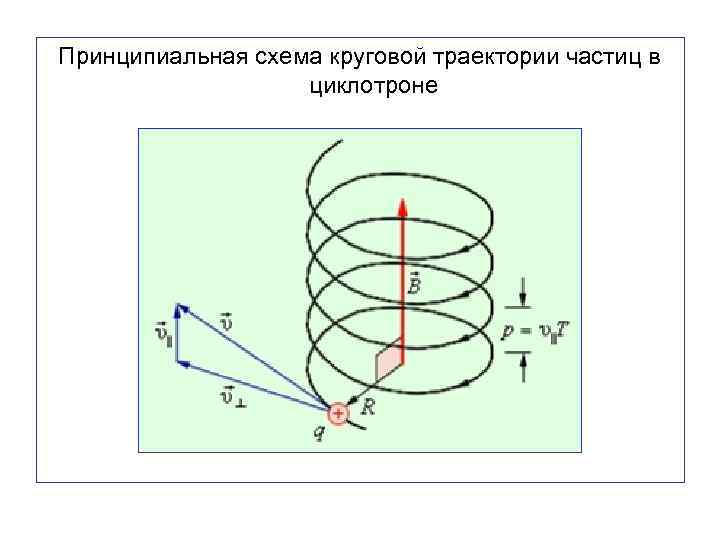Принципиальная схема круговой траектории частиц в циклотроне Принципиальная схема круговой траектории частиц в циклотроне

Таким образом, в циклотроне заряженная частица: - ускоряется электрическим полем; - удерживается на траектории Таким образом, в циклотроне заряженная частица: - ускоряется электрическим полем; - удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 Мэ. В (1 э. В = 1, 6 10 -19 Дж). При большой скорости частиц масса частиц начинает возрастать с увеличением скорости:

Циклотронная частота при этом начинает уменьшаться. Вслед за ней нужно уменьшать частоту переменного ускоряющего Циклотронная частота при этом начинает уменьшаться. Вслед за ней нужно уменьшать частоту переменного ускоряющего напряжения. Для этого созданы сложные электронные устройства, которые уменьшают частоту переменного напряжения по мере того, как скорость пучка заряженных частиц нарастает. Такой усовершенствованный циклотрон называется синхроциклотроном или просто фазотроном.

В синхрофазотронах используется способ «борьбы» с возрастание массы частиц по мере увеличения их скорости, В синхрофазотронах используется способ «борьбы» с возрастание массы частиц по мере увеличения их скорости, основанный на увеличении магнитной индукции по мере ускорения частиц. Частицы предварительно ускоряют в небольшом ускорителе. Затем постепенно увеличивают магнитное поле по мере их дальнейшего ускорения в гигантском синхрофазотроне. В синхрофазотроне частицы движутся по орбите постоянного радиуса порядка 1 км. Протоны ускоряются до энергий 1000 Мэ. В.

3. 6. Работа сил магнитного поля 1. Рассмотрим перемещение прямого проводника с током длины 3. 6. Работа сил магнитного поля 1. Рассмотрим перемещение прямого проводника с током длины L в магнитном поле, силовые линии которого направлены к нам. Если проводник не закреплён, то под действием силы Ампера он переместится в магнитном поле на расстояние dx. При этом сила Ампера совершит элементарную работу:

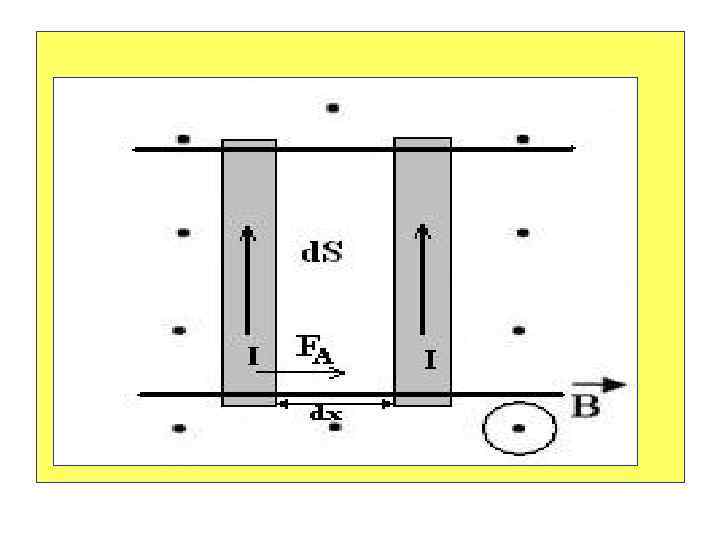
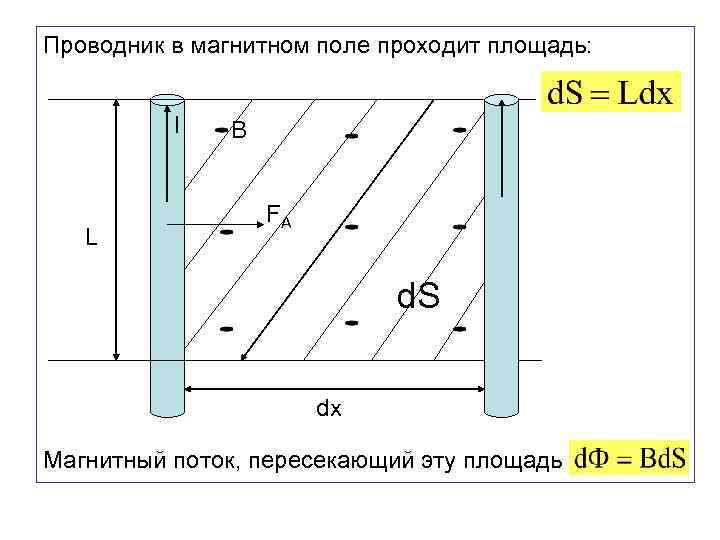Проводник в магнитном поле проходит площадь: I L B FA d. S dx Магнитный Проводник в магнитном поле проходит площадь: I L B FA d. S dx Магнитный поток, пересекающий эту площадь

Тогда элементарная работа . Полная работа на конечном перемещении: Ф – магнитный поток через Тогда элементарная работа . Полная работа на конечном перемещении: Ф – магнитный поток через всю площадь, пересекаемую проводником в магнитном поле. Работа магнитных сил по перемещению прямого проводника с током равна произведению силы тока на магнитный поток через площадь, пересекаемую проводником в магнитном поле.

2. Рассмотрим перемещение замкнутого контура с током, который изменяет свою конфигурацию в магнитном поле. 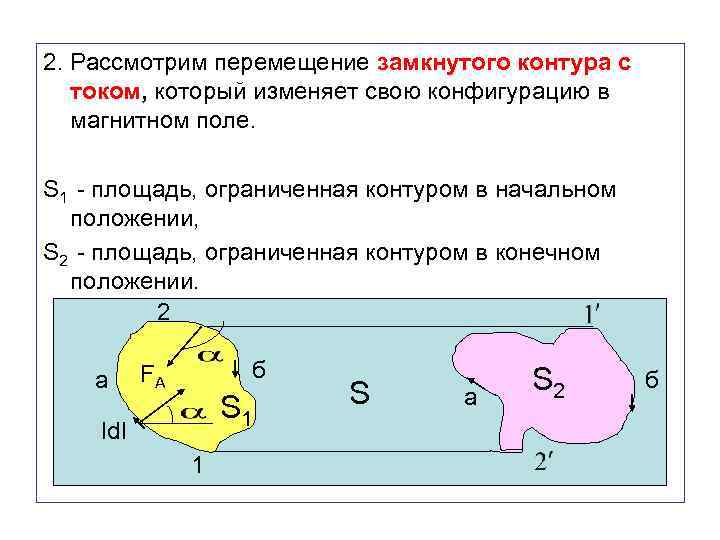2. Рассмотрим перемещение замкнутого контура с током, который изменяет свою конфигурацию в магнитном поле. S 1 - площадь, ограниченная контуром в начальном положении, S 2 - площадь, ограниченная контуром в конечном положении. 2 a б FA S 1 Idl 1 S а S 2 б

Разобьём замкнутый контур на две части: 1 а 2 и 2 б 1. На Разобьём замкнутый контур на две части: 1 а 2 и 2 б 1. На элементы тока участка контура 1 а 2 действует сила Ампера, направленная под острым углом к вектору элементарного перемещения. Работа этой силы по перемещению всего участка 1 а 2 будет положительной и равной: Ф 1 – магнитный поток через площадь контура S 1 , Ф – магнитный поток через площадь S, заключённую между начальным и конечным положениями контура.

На элементы участка контура 2 б 1 действует сила Ампера, направленная под тупым углом На элементы участка контура 2 б 1 действует сила Ампера, направленная под тупым углом к вектору элементарного перемещения. Работа силы Ампера по перемещению всего участка 2 б 1 будет отрицательной и равной: Ф 2 – магнитный поток через площадь S 2. Полная работа:

Окончательно Работа сил магнитного поля по перемещению замкнутого контура с током в магнитном поле Окончательно Работа сил магнитного поля по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока на изменение магнитного потока через площадь, ограниченную контуром в начальном и конечном положениях.