Multigrid Eigensolvers for Image Segmentation Andrew Knyazev Supported

Multigrid Eigensolvers for Image Segmentation Andrew Knyazev Supported by NSF DMS 0612751. This presentation is at http: //math. ucdenver. edu/~aknyazev/research/conf/. 1

2 Eigensolvers for image segmentation: Image Segmentation – the definition Image Segmentation as Clustering: how? Spectral clustering and partitioning Partitioning as image segmentation Eigensolvers for spectral clustering Multi-resolution image segmentation References Conclusions

3 Image Segmentation – the definition Wikipedia: In computer vision, segmentation refers to the process of partitioning a digital image into multiple segments (sets of pixels). Image segmentation is the process of assigning a label to every pixel in an image such that pixels with the same label (i. e. in the same segment) share certain visual characteristics. All pixels in a segment are similar with respect to some characteristic or computed properties, such as color, intensity, or texture. Adjacent segments are significantly different with respect to the same characteristic(s).

4 Image Segmentation as Clustering A specific case of general Data Clustering, where data points are the image pixels Geometric location of each pixel within the image is KNOWN a priori The similarity among the (typically only neighborhood) pixels is calculated using some function which for every two (neighborhood) pixels i and j determines a number a_ij between 0 and 1. If a_ij = 0, there is no similarity between the two pixels. On the other extreme, if a_ij = 1, the two pixels are “the same. ” Weighted graph: vertices-pixels, edges-a_ij

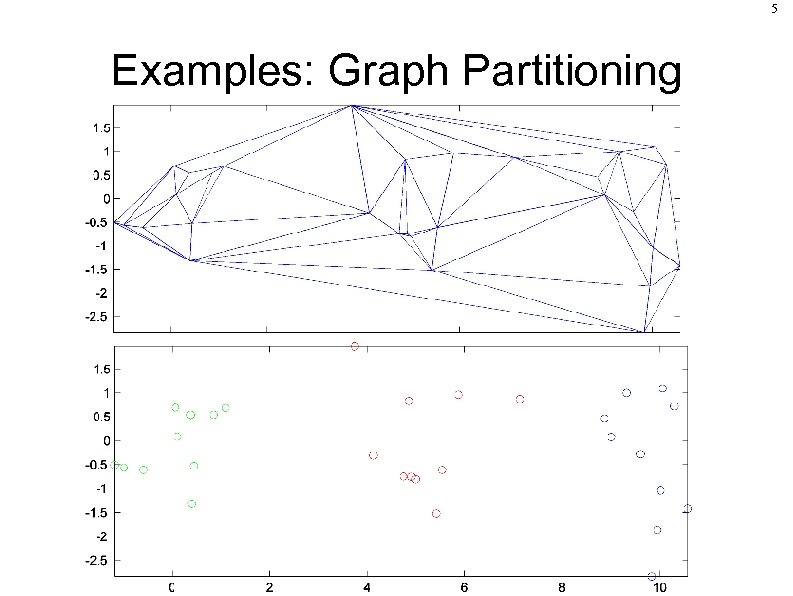5 Examples: Graph Partitioning

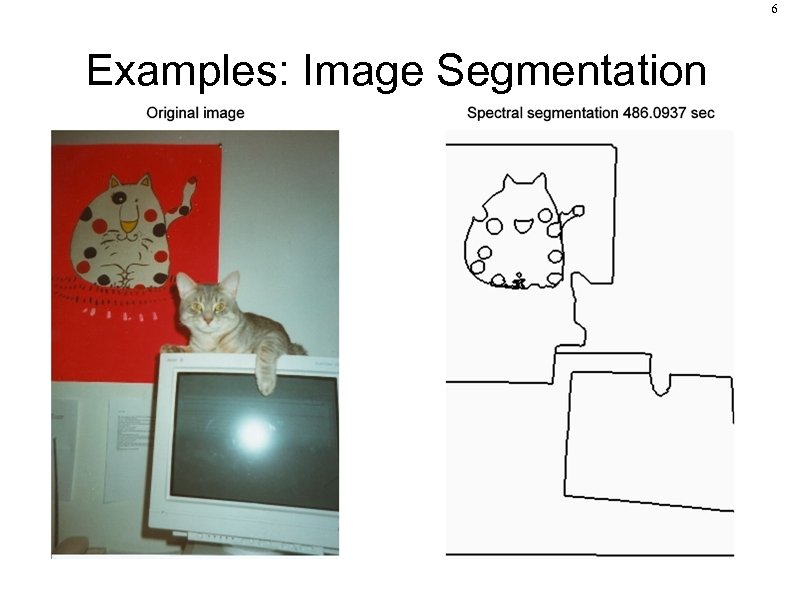6 Examples: Image Segmentation

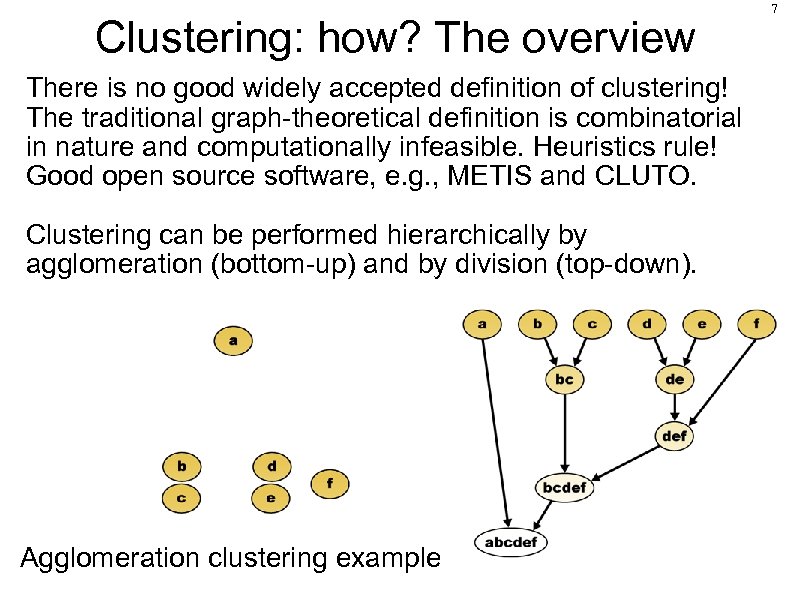Clustering: how? The overview There is no good widely accepted definition of clustering! The traditional graph-theoretical definition is combinatorial in nature and computationally infeasible. Heuristics rule! Good open source software, e. g. , METIS and CLUTO. Clustering can be performed hierarchically by agglomeration (bottom-up) and by division (top-down). Agglomeration clustering example 7

8 Clustering: how? Algorithms Partitioning means determining clusters. Partitioning can be used recursively for hierarchical division (top-down). Many partitioning methods are known. Here we cover: K-means (centroids) Spectral partitioning using Fiedler vectors = Principal Components Analysis (PCA) PCA/spectral partitioning is known to produce high quality clusters, but is considered to be expensive as solution of large-scale eigenproblems is required. Our expertise in eigensolvers comes to the rescue!

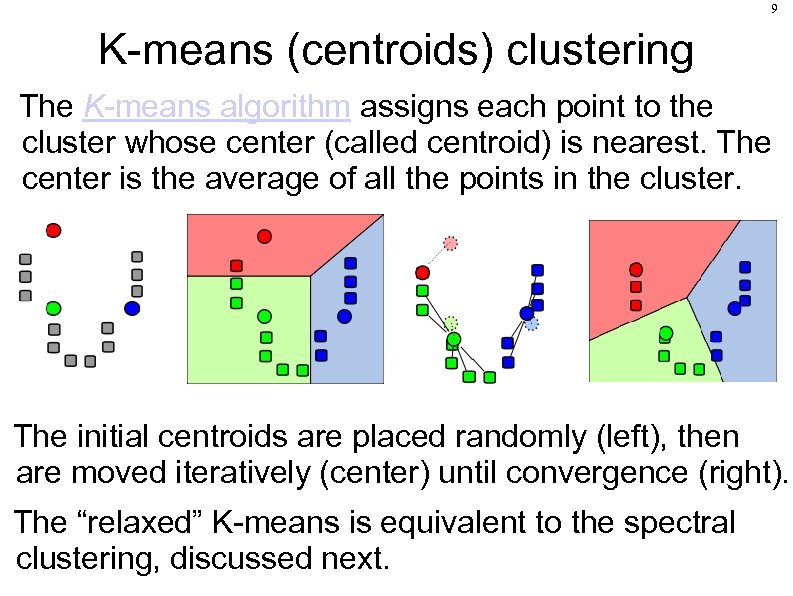9 K-means (centroids) clustering The K-means algorithm assigns each point to the cluster whose center (called centroid) is nearest. The center is the average of all the points in the cluster. The initial centroids are placed randomly (left), then are moved iteratively (center) until convergence (right). The “relaxed” K-means is equivalent to the spectral clustering, discussed next.

10 Eigenproblems in mechanical vibrations Free transversal vibration without damping of the mass-spring system is described by the ODE system Standing wave assumption leads to the eigenproblem Component xi describes the up-down movement of mass i. Images courtesy http: //www. gps. caltech. edu/~edwin/Molecule. HTML/Au. Cl 4_html/Au. Cl 4_page. html

Spectral clustering in mechanics The main idea comes from mechanical vibrations and is intuitive: in the spring-mass system the masses which are tightly connected will have the tendency to move together synchronically in low-frequency free vibrations. Analysing the signs of the components corresponding to different masses of the low-frequency vibration modes of the system allows us to determine the clusters of the masses! A 4 -degree-of-freedom system has 4 modes of vibration and 4 natural frequencies: partition into 2 clusters using the second eigenvector: Images Courtesy: Russell, Ketteriung U. 11

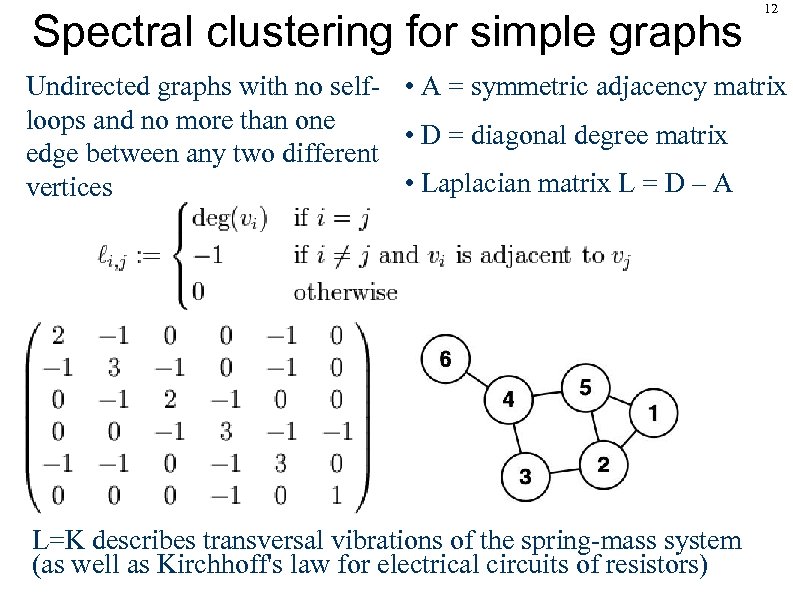Spectral clustering for simple graphs 12 Undirected graphs with no self- • A = symmetric adjacency matrix loops and no more than one • D = diagonal degree matrix edge between any two different • Laplacian matrix L = D – A vertices L=K describes transversal vibrations of the spring-mass system (as well as Kirchhoff's law for electrical circuits of resistors)

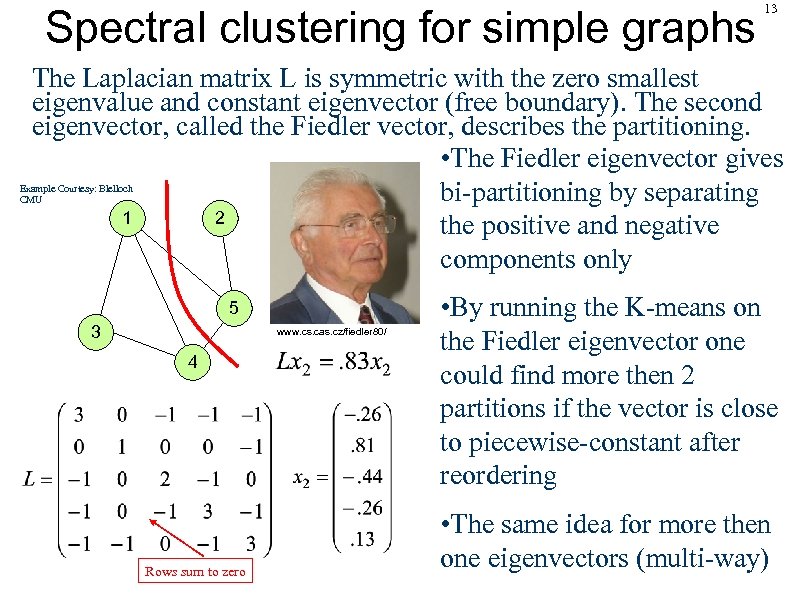Spectral clustering for simple graphs 13 The Laplacian matrix L is symmetric with the zero smallest eigenvalue and constant eigenvector (free boundary). The second eigenvector, called the Fiedler vector, describes the partitioning. • The Fiedler eigenvector gives bi-partitioning by separating 1 2 the positive and negative components only Example Courtesy: Blelloch CMU 5 3 www. cs. cas. cz/fiedler 80/ 4 Rows sum to zero • By running the K-means on the Fiedler eigenvector one could find more then 2 partitions if the vector is close to piecewise-constant after reordering • The same idea for more then one eigenvectors (multi-way)

14 PCA clustering for simple graphs • The Fiedler vector is an eigenvector of Lx=λx, in the springmass system this corresponds to the stiffness matrix K=L and to the mass matrix M=I (identity) • Should not the masses with a larger adjacency degree be heavier? Let us take the mass matrix M=D -the degree matrix • So-called N-cut smallest eigenvectors of Lx=λDx are the largest for Ax=µDx with µ=1 -λ since L=D-A • PCA for D-1 A computes the largest eigenvectors, which then can be used for clustering by the K-means • D-1 A is row-stochastic and describes the Markov random walk probabilities on the simple graph

15 Partitioning as image segmentation Image pixels serve as graph vertices. We generate a sparse Laplacian, by comparing neighboring only 5 or 9 pixels here when calculating the weights for the edges by comparing pixel colors. Here is an example displaying on the right 4 Fiedler vectors of an image on the left. The actual values of vectors’ components are shown at every pixel.

16 Eigensolvers for spectral clustering Our BLOPEX-LOBPCG software has proved to be efficient for large-scale eigenproblems for Laplacians from PDE's and for image segmentation using multiscale preconditioning of hypre The LOBPCG for massively parallel computers is available in our Block Locally Optimal Preconditioned Eigenvalue Xolvers (BLOPEX) package BLOPEX is built-in in http: //www. llnl. gov/CASC/hypre/ and is included as an external package in PETSc, see http: //www-unix. mcs. anl. gov/petsc/ On Blue. Gene/L 1024 CPU we can compute the Fiedler vector of a 24 megapixel image in seconds (including the hypre algebraic multigrid setup).

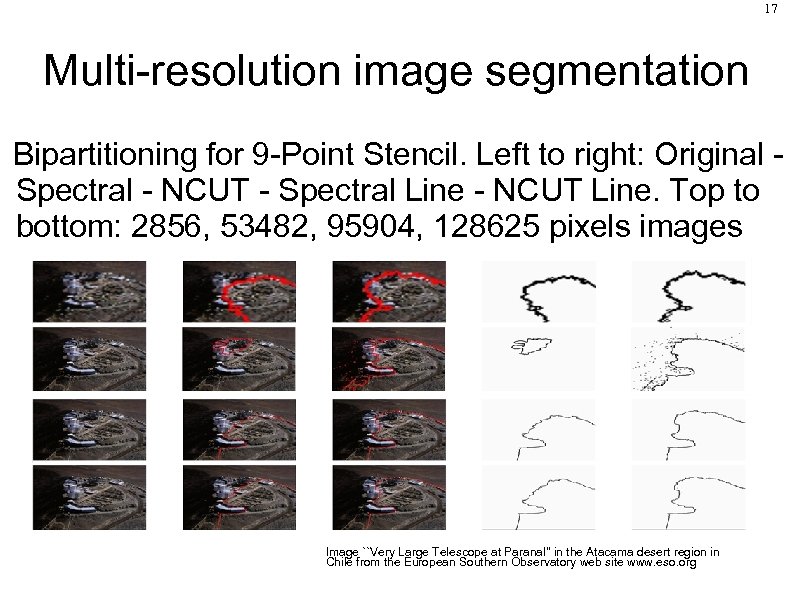17 Multi-resolution image segmentation Bipartitioning for 9 -Point Stencil. Left to right: Original Spectral - NCUT - Spectral Line - NCUT Line. Top to bottom: 2856, 53482, 95904, 128625 pixels images Image ``Very Large Telescope at Paranal'' in the Atacama desert region in Chile from the European Southern Observatory web site www. eso. org

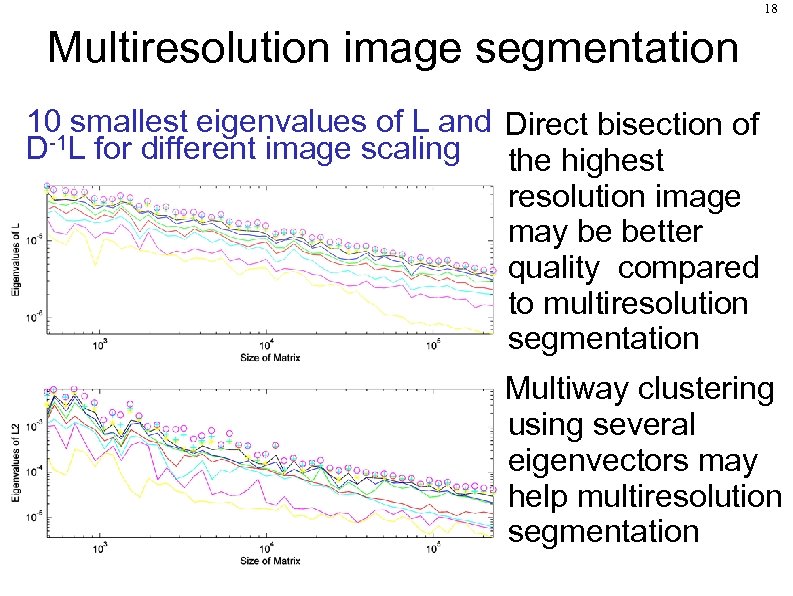18 Multiresolution image segmentation 10 smallest eigenvalues of L and Direct bisection of D-1 L for different image scaling the highest resolution image may be better quality compared to multiresolution segmentation Multiway clustering using several eigenvectors may help multiresolution segmentation

19 References AK, Toward the Optimal Preconditioned Eigensolver: Locally Optimal Block Preconditioned Conjugate Gradient Method. SISC 23 (2001), 517 -541. AK and K. Neymeyr, Efficient solution of symmetric eigenvalue problems using multigrid preconditioners in the locally optimal block conjugate gradient method. ETNA, 15 (2003), 38 -55. AK, I. Lashuk, M. E. Argentati, and E. Ovchinnikov, Block Locally Optimal Preconditioned Eigenvalue Xolvers (BLOPEX) in hypre and PETSc. SISC. 25(2007), 2224 -2239.

20 Recommended general reading Internet search for Spectral Clustering, Graph Partitioning, Image Segmentation, Normalized Cuts Spectral Clustering, Ordering and Ranking: Statistical Learning with Matrix Factorizations by Chris Ding and Hongyuan Zha, Springer, In Press. ISBN-13: 978 -0387304489 These slides and other similar talks on my Web at http: //math. ucdenver. edu/~aknyazev/research/conf/

21 Possible Future Work Code a similar driver using Hypre geometric multigrid preconditioner rather than algebraic Develop and code in-house geometric multigrid specifically for image segmentation purposes No need for double precision: code a single precision driver In a dedicated image segmentation package, all calculations must be performed using a precision that matches the image format (great for GPUs!) Crucial mathematical issues not discussed here

22 Conclusions Spectral Clustering is an intuitive and powerful tool for image segmentation. Our eigenxolvers efficiently perform image segmentation using Hypre’s algebraic multigrid preconditioning on parallel computers. Segmentation using smaller resolutions of the same image, e. g. , to construct initial approximations for higher resolutions, could accelerate the process, but requires multi-way computations involving several eigenvectors.