Multicell Squall-Line Structure as a Manifestation of Vertically

Multicell Squall-Line Structure as a Manifestation of Vertically Trapped Gravity Waves Ming-Jen Yang and Robert A. House Jr. Mon. Wea. Rev. , 123, 641 -661 Hsiao-Ling Huang 2003/12/29

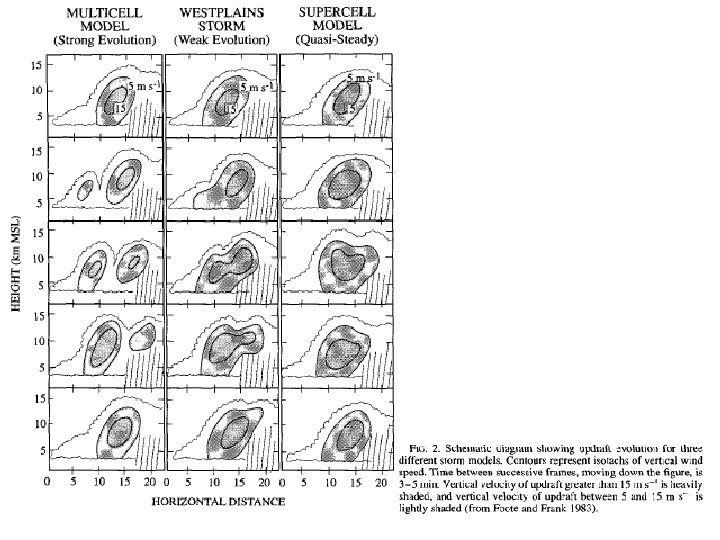
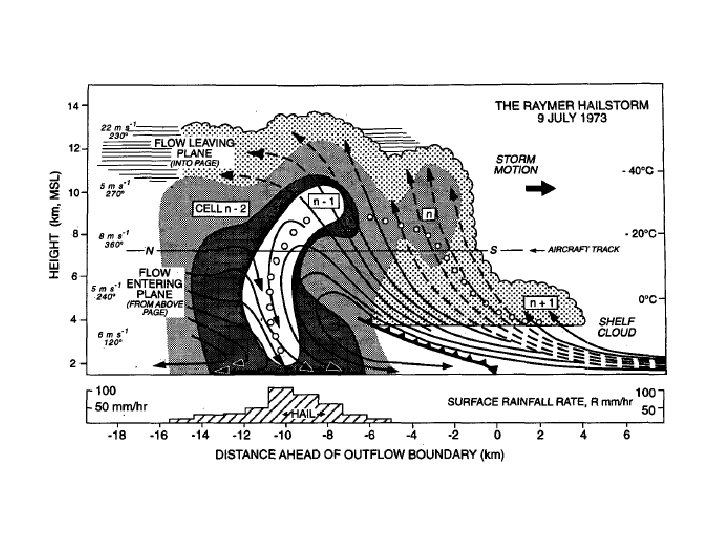
Introduction • Byers and Braham(1949) identified three stages in the evolution of an ordinary cell: the cumulus stage (updraft alone), the mature stage (updraft and downdraft), and the dissipating stage (downdraft alone). • Fovell and Ogura(1988): individual cells moved rearward relative to the gust front as they aged, transporting hydrometeors in their updrafts into the trailing portion of the storm, and the new cells cutting off the moisture supply of the older cells. • The gravity wave structure excited by convection of the squall line system(1985/06/10~11), which is the focus of this study.

Numerical model and initial conditions Numerical model • Compressible nonhydrostatic cloud model, microphysical bulk parameterization, ice-phase microphysics is included. • Both 2 D and 3 Dversions of the model. • 2 D simulation: grid points: 455 (H) × 62 (V) Δ z = 550 m domain: 4814 km(H)× 21. 7 km(V) Fine mesh=1 km Stretch grid is 1. 075: 1 2250 km 314 km 2250 km Δ z = 140 m

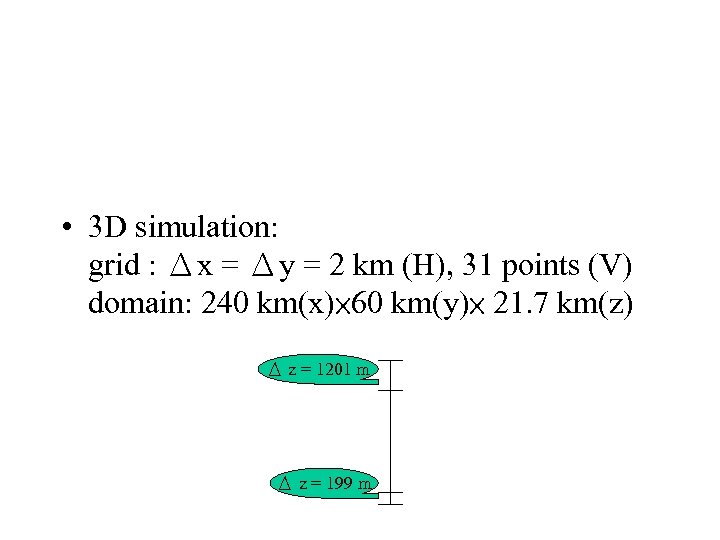• 3 D simulation: grid : Δx = Δy = 2 km (H), 31 points (V) domain: 240 km(x)× 60 km(y)× 21. 7 km(z) Δ z = 1201 m Δ z = 199 m

Initial conditions 1985/06/10/2331 UTC [Enid(END), Oklahoma]. T, TD, u, v 1985/06/10/2330 UTC [Pratt(PTT), Kansas]. Low-level moisture 1985/06/10~11

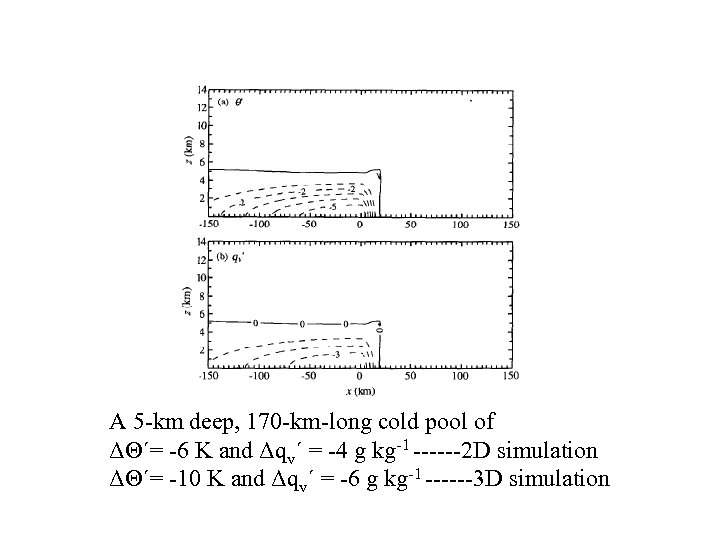A 5 -km deep, 170 -km-long cold pool of ΔΘ´= -6 K and Δqv´ = -4 g kg-1 ------2 D simulation ΔΘ´= -10 K and Δqv´ = -6 g kg-1 ------3 D simulation

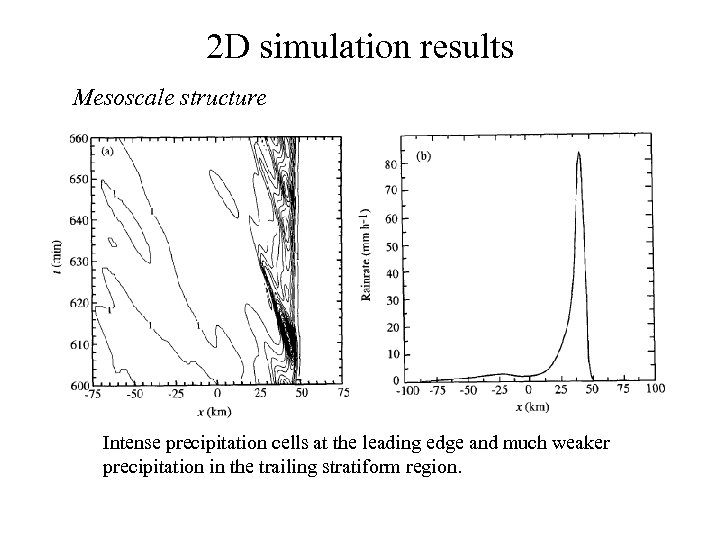2 D simulation results Mesoscale structure Intense precipitation cells at the leading edge and much weaker precipitation in the trailing stratiform region.

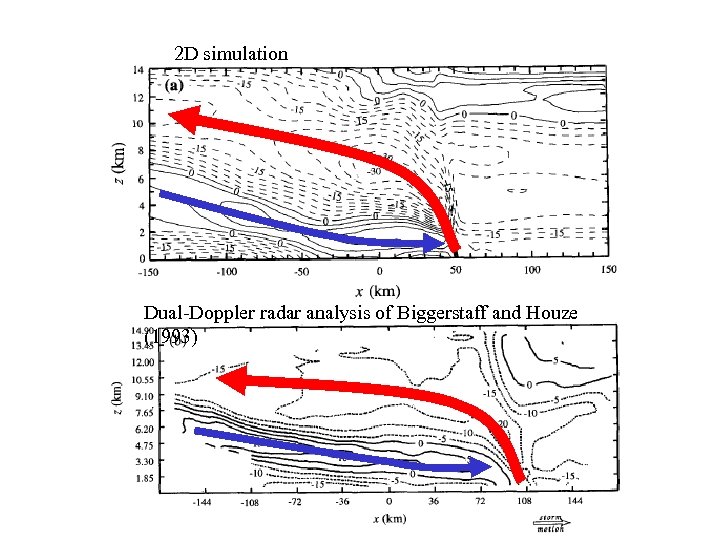2 D simulation Dual-Doppler radar analysis of Biggerstaff and Houze (1993)

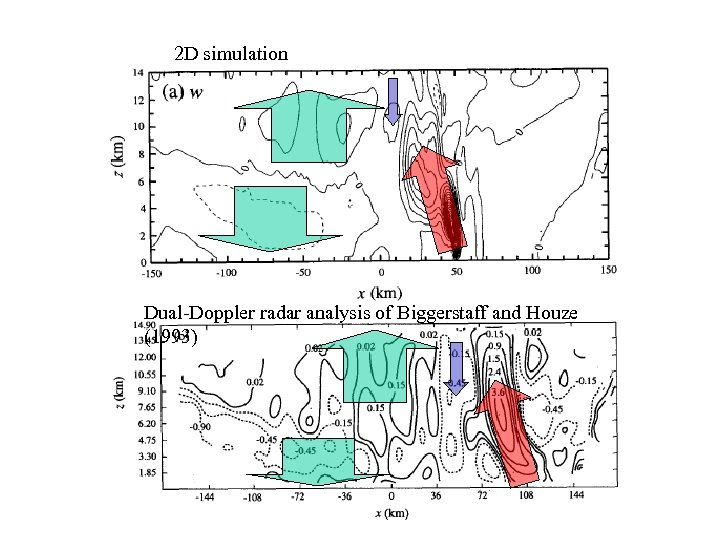2 D simulation Dual-Doppler radar analysis of Biggerstaff and Houze (1993)

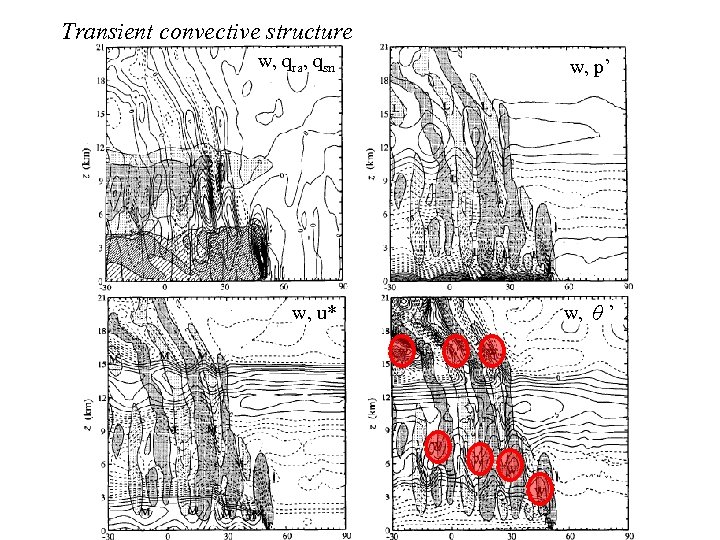Transient convective structure w, qra, qsn w, p’ w, u* w, θ’

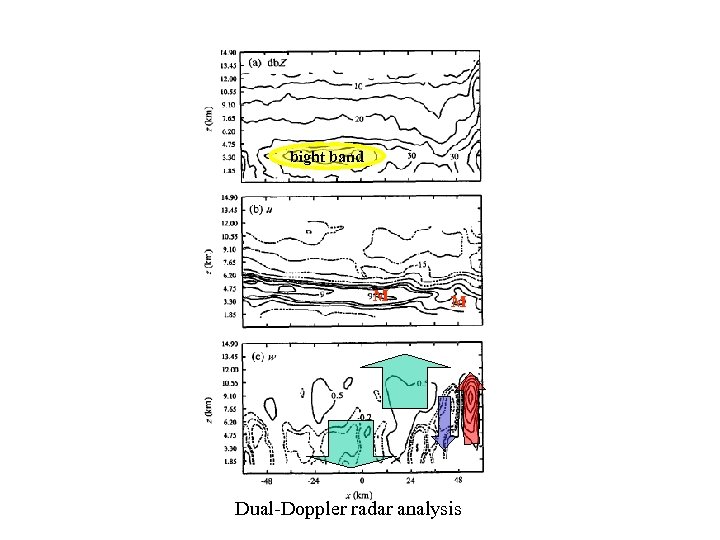bight band M M Dual-Doppler radar analysis

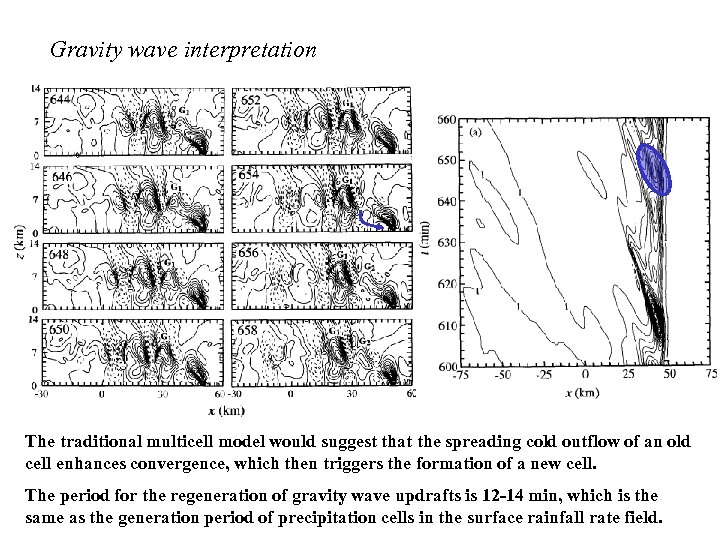Gravity wave interpretation The traditional multicell model would suggest that the spreading cold outflow of an old cell enhances convergence, which then triggers the formation of a new cell. The period for the regeneration of gravity wave updrafts is 12 -14 min, which is the same as the generation period of precipitation cells in the surface rainfall rate field.

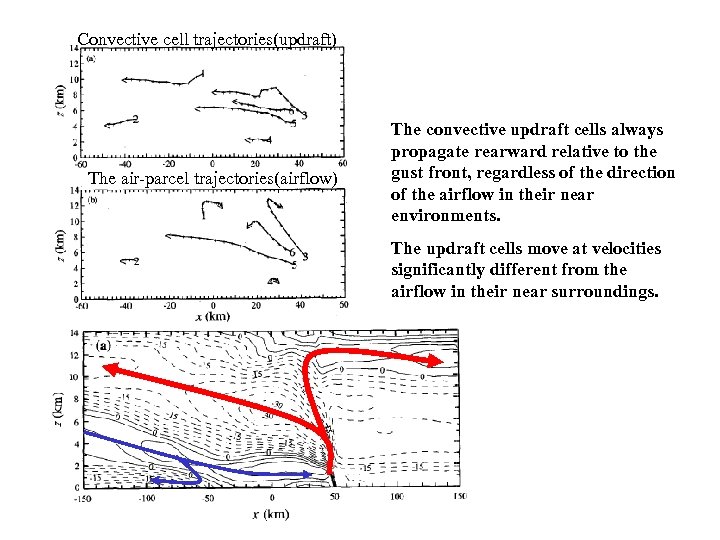Convective cell trajectories(updraft) The air-parcel trajectories(airflow) The convective updraft cells always propagate rearward relative to the gust front, regardless of the direction of the airflow in their near environments. The updraft cells move at velocities significantly different from the airflow in their near surroundings.

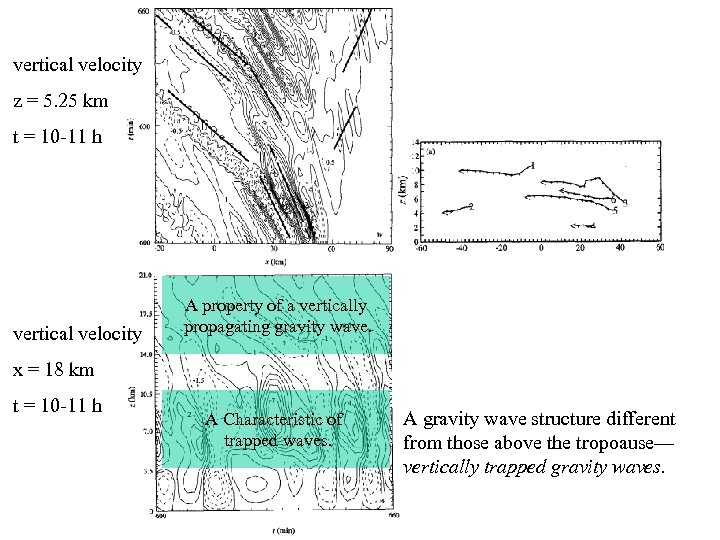vertical velocity z = 5. 25 km t = 10 -11 h vertical velocity A property of a vertically propagating gravity wave. x = 18 km t = 10 -11 h A Characteristic of trapped waves. A gravity wave structure different from those above the tropoause— vertically trapped gravity waves.

Three-dimensional simulation results 3 D, Z = 6. 3 km , t = 5 h 2 D, t = 11 h w, qra, qsn The heavy line is the surface gust front determined by the θ’ = -1

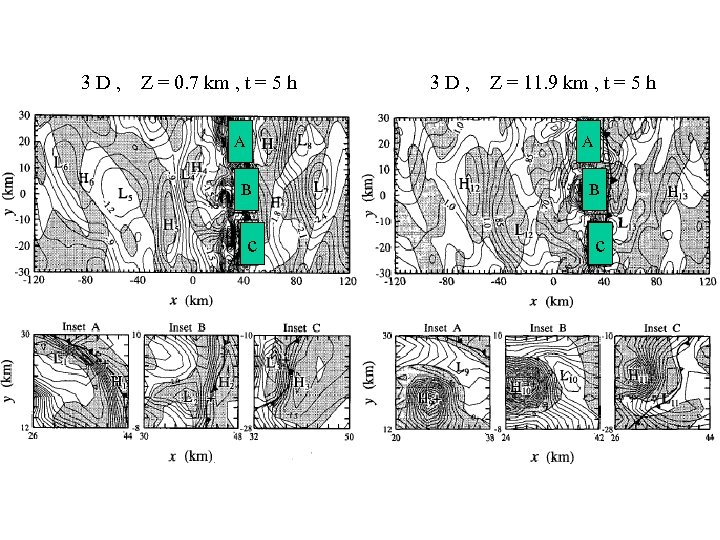3 D, Z = 0. 7 km , t = 5 h A 3 D, Z = 11. 9 km , t = 5 h A B c

Linear theory presentation of model gravity waves π : nondimensional pressure N : Brunt-Väisälä(bouyancy) frequency cs : basic-state sound speed are functions of z Q : the latent heating produced by convection.

To remove the effect of the decrease in density with height by defining new variables (Bretherton 1966):

when cs →∞, then (10) can be written in a simpler form, and eliminate A 1 A 2

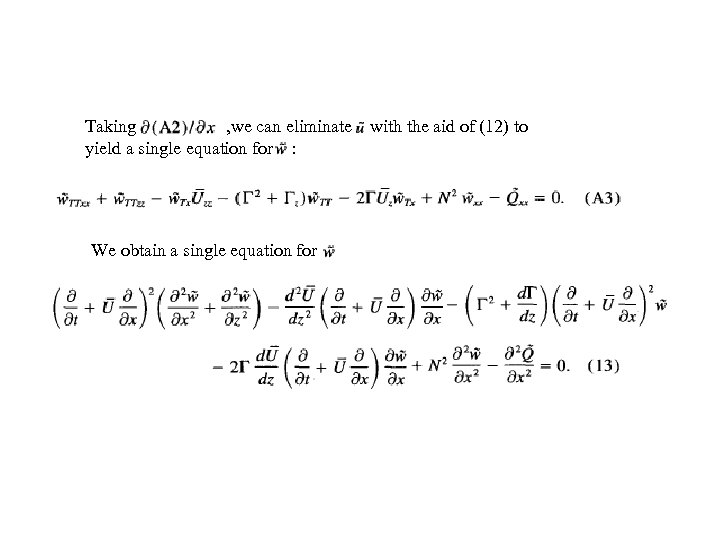Taking , we can eliminate yield a single equation for : We obtain a single equation for with the aid of (12) to

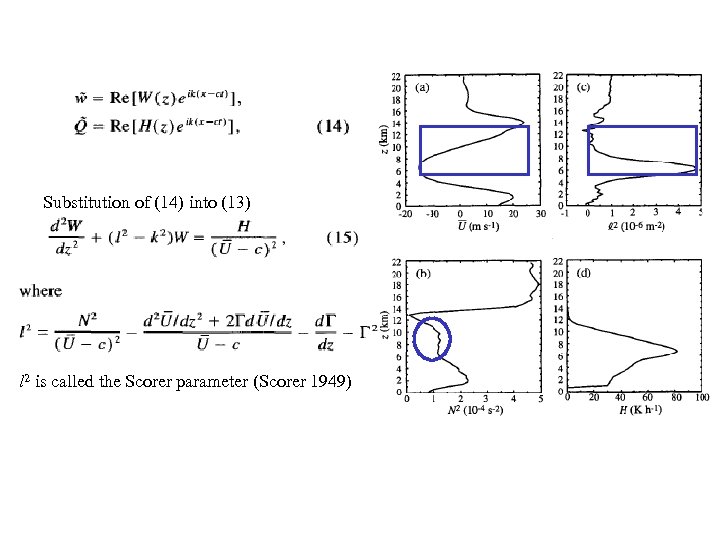Substitution of (14) into (13) l 2 is called the Scorer parameter (Scorer 1949)

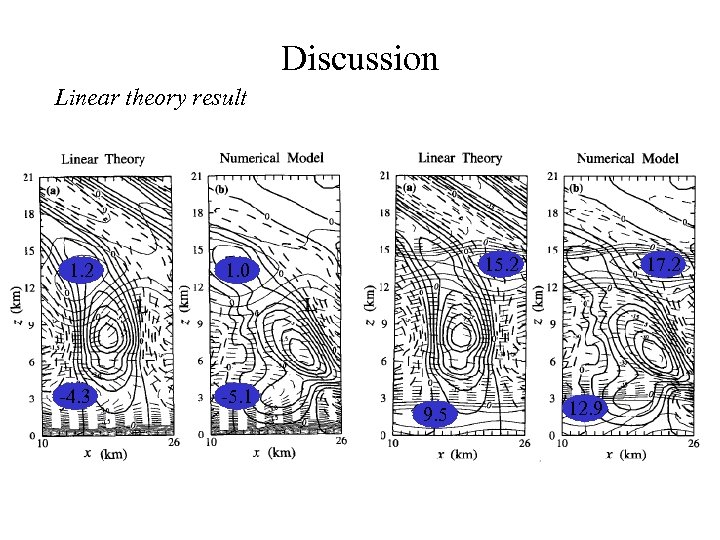Discussion Linear theory result 1. 2 -4. 3 -5. 1 15. 2 1. 0 9. 5 17. 2 12. 9

Characteristics of trapped waves in the simulated squall line The leading portion of the simulated squall line: horizontal wavelengths λ = 16 ~ 20 km, storm-relative phase speeds c = -20 ~ -25 ms-1, the main gravity wave periods T = λ/c =10. 7 ~ 16. 7 min. The trailing stratiform region(with weaker amplitudes): horizontal wavelengths λ = 25 ~ 35 km, storm-relative phase speeds c = -30 ~ -40 ms-1. The period of convective cells are the same as the gravity wave periods.

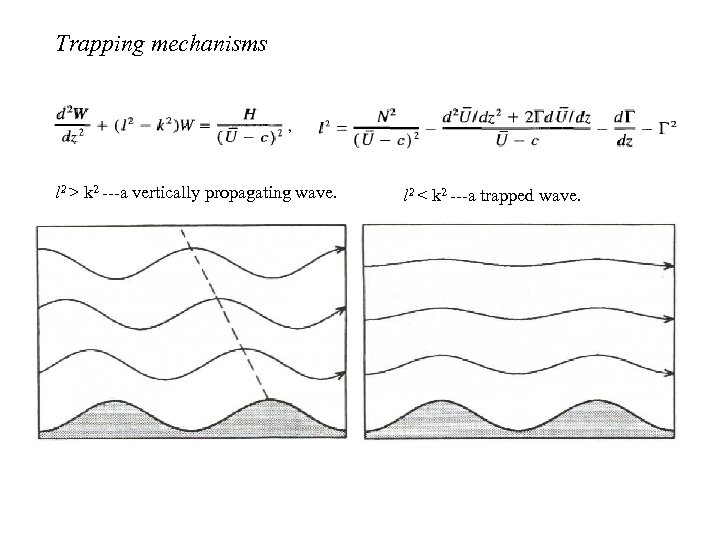Trapping mechanisms l 2 > k 2 ---a vertically propagating wave. l 2 < k 2 ---a trapped wave.

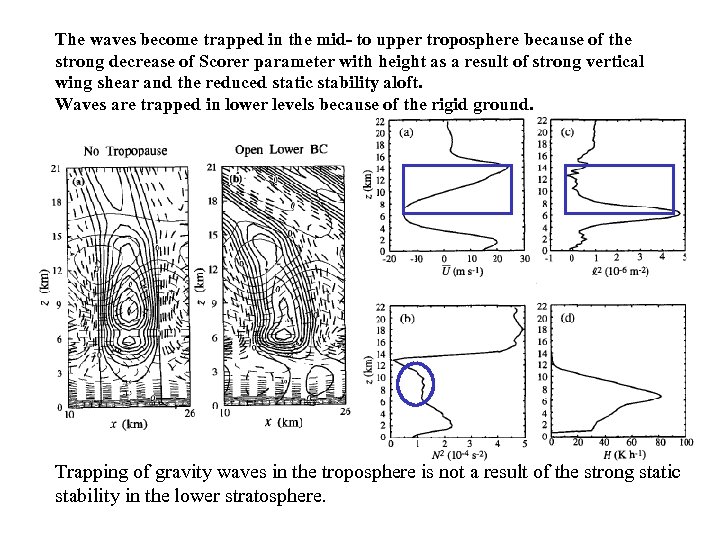The waves become trapped in the mid- to upper troposphere because of the strong decrease of Scorer parameter with height as a result of strong vertical wing shear and the reduced static stability aloft. Waves are trapped in lower levels because of the rigid ground. Trapping of gravity waves in the troposphere is not a result of the strong static stability in the lower stratosphere.

Conclusion • The old cell dissipates when a new cell appears ahead if it along the gust front and “cuts off” the old cell’s supply of moisture and buoyant air. • The convectional interpretation of the cutoff process is actually a gravity wave phenomenon. Updraft cells behind this low-level leading edge updraft are transient gravity wave features. • Convective cells in the troposphere exhibit a quadrature relationship between the w and p’ (or u*) fields that indicates they are vertically trapped gravity waves(mid- to upper-troposphere).

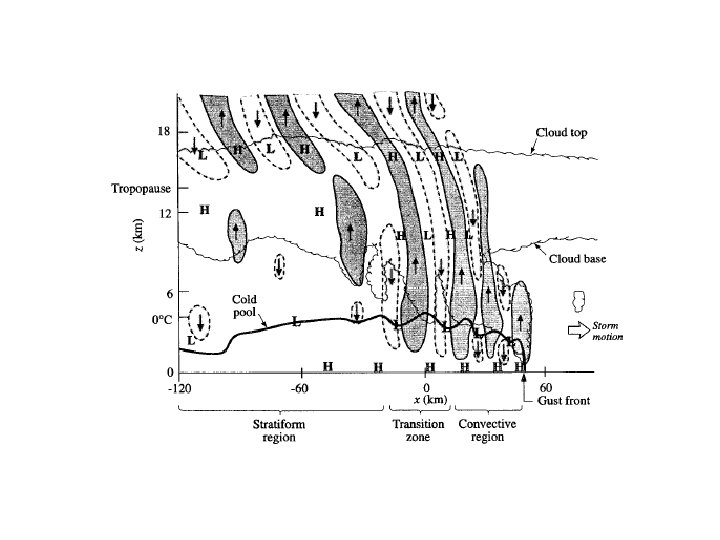
• In the trailing stratiform region, the amplitudes of these gravity waves become weaker, but their wavelengths become longer with faster phase speeds. • The gravity wave explanation for the multicellular structure of thunderstorms and squall lines may lead to a new understanding of convective momentum transport.