Multi-way Anova Identifying and quantifying sources of

Multi-way Anova • Identifying and quantifying sources of variation • Ability to "factor out" certain sources - ("adjusting") • For the beginning, we will reproduce paired t-test results by assuming that arrays are one of the factors in a Two-way ANOVA • Second, adjusting for the dye effects in a Three-way ANOVA • Third, four and more - way ANOVA when having multiple factors of interest 1 -20 -05 1

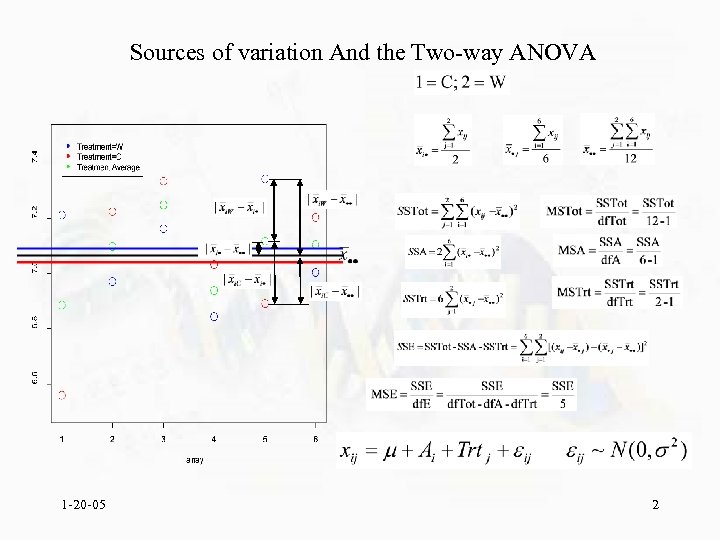Sources of variation And the Two-way ANOVA 1 -20 -05 2

Statistical Inference in Two-way ANOVA Statistical Model Parameter Estimates Null Hypotheses Null Distributions 1 -20 -05 3

Alternative Formulations of the Two-way ANOVA No-intercept Model Null Hypotheses Null Distributions Parameter Estimates • Gets complicated • Regardless of how the model is parametrized certain parameters remain unchanged (Trt 2 -Trt 1) • In this sense all formulations are equivalent 1 -20 -05 4

Re-organizing data for ANOVA > DAnova<-NNBLimmadata. C > DAnova$weights<-cbind(DAnova$weights, DAnova$weights) > DAnova$M<-cbind((DAnova$A+DAnova$M/2), DAnova$A-(DAnova$M/2)) > DAnova$A<-cbind(DAnova$A, DAnova$A) > attributes(DAnova) $names [1] "weights" "targets" "genes" "printer" "M" "A" $class [1] "MAList" attr(, "package") [1] "limma" > NNBLimmadata. C$M[1, ] 51 -C 1 -3 -vs-W 1 -5 60 -W 2 -3 -vs-C 2 -5 72 -C 3 -3 -vs-W 3 -5 79 -W 4 -3 -vs-C 4 -5 82 -C 5 -3 -vs-W 5 -5 97 -W 6 -3 -vs-C 6 -5 -0. 05280598 -0. 15767422 0. 40130216 -0. 35292771 -0. 22061576 -0. 21653047 > NNBLimmadata. C$A[1, ] 51 -C 1 -3 -vs-W 1 -5 60 -W 2 -3 -vs-C 2 -5 72 -C 3 -3 -vs-W 3 -5 79 -W 4 -3 -vs-C 4 -5 82 -C 5 -3 -vs-W 5 -5 97 -W 6 -3 -vs-C 6 -5 6. 289658 6. 129577 6. 483613 6. 452317 6. 510143 7. 106134 > DAnova$M[1, ] 51 -C 1 -3 -vs-W 1 -5 60 -W 2 -3 -vs-C 2 -5 72 -C 3 -3 -vs-W 3 -5 79 -W 4 -3 -vs-C 4 -5 82 -C 5 -3 -vs-W 5 -5 97 -W 6 -3 -vs-C 6 -5 6. 263255 6. 050740 6. 684264 6. 275853 6. 399835 6. 997869 51 -C 1 -3 -vs-W 1 -5 60 -W 2 -3 -vs-C 2 -5 72 -C 3 -3 -vs-W 3 -5 79 -W 4 -3 -vs-C 4 -5 82 -C 5 -3 -vs-W 5 -5 97 -W 6 -3 -vs-C 6 -5 6. 316061 6. 208414 6. 282962 6. 628781 6. 620451 7. 214399 1 -20 -05 5

Setting-up the design matrix for limma > targets Slide. Number 51 -C 1 -3 -vs-W 1 -5 60 -W 2 -3 -vs-C 2 -5 72 -C 3 -3 -vs-W 3 -5 79 -W 4 -3 -vs-C 4 -5 82 -C 5 -3 -vs-W 5 -5 97 -W 6 -3 -vs-C 6 -5 File. Name Cy 3 Cy 5 51 51 -C 1 -3 -vs-W 1 -5. gpr 60 60 -W 2 -3 -vs-C 2 -5. gpr 72 72 -C 3 -3 -vs-W 3 -5. gpr 79 79 -W 4 -3 -vs-C 4 -5. gpr 82 82 -C 5 -3 -vs-W 5 -5. gpr 97 97 -W 6 -3 -vs-C 6 -5. gpr Date C W 11/8/2004 W C 11/8/2004 > trt<-c(targets$Cy 5, targets$Cy 3) > trt [1] "W" "C" "W" "C" "W" > array<-c(1: 6, 1: 6) > array [1] 1 2 3 4 5 6 1 -20 -05 6

Setting-up the design matrix for limma > designa<-model. matrix(~-1+factor(array)+factor(trt)) > designa factor(array)1 factor(array)2 factor(array)3 factor(array)4 factor(array)5 factor(array)6 factor(trt)W 1 1 0 0 0 1 2 0 1 0 0 0 3 0 0 1 0 0 0 1 4 0 0 0 1 0 0 0 5 0 0 1 0 1 6 0 0 0 1 0 7 1 0 0 0 8 0 1 0 0 1 9 0 0 10 0 1 11 0 0 12 0 0 0 1 1 attr(, "assign") [1] 1 1 1 2 attr(, "contrasts")$"factor(array)" [1] "contr. treatment" attr(, "contrasts")$"factor(trt)" [1] "contr. treatment" 1 -20 -05 7

designa" src="https://present5.com/presentation/777583256f3e4a245c0ee3b7918f1fbe/image-8.jpg" alt="Setting-up the design matrix for limma > colnames(designa)<-c(paste("A", 1: 6, sep=""), "W") > designa" /> Setting-up the design matrix for limma > colnames(designa)<-c(paste("A", 1: 6, sep=""), "W") > designa A 1 A 2 A 3 A 4 A 5 A 6 W 1 1 0 0 01 2 0 1 0 00 3 0 0 1 0 0 01 4 0 0 0 1 0 00 5 0 0 1 01 6 0 0 0 10 7 1 0 0 00 8 0 1 0 01 9 0 0 1 0 0 00 10 0 1 11 0 0 12 0 0 0 1 1 attr(, "assign") [1] 1 1 1 2 attr(, "contrasts")$"factor(array)" [1] "contr. treatment" attr(, "contrasts")$"factor(trt)" [1] "contr. treatment" 1 -20 -05 8

Comparing to paired t-test > Anova<-lm. Fit(DAnova, designa) > > Anova$coefficients[2, ] A 1 A 2 A 3 A 4 A 5 A 6 W 8. 36197475 9. 90627295 11. 34002704 10. 77586480 9. 35096212 9. 92299117 -0. 03068036 > Limma. PTT$coefficients[2] [1] -0. 03068036 > Anova$coefficients[1, ] A 1 A 2 A 3 A 4 A 5 A 6 W NA NA 6. 3898451 6. 3585492 6. 4163747 7. 0123661 0. 1875361 > Limma. PTT$coefficients[1] 0. 1875361 > 1 -20 -05 9

plot(Anova$sigma, Limma. PTT$sigma) >" src="https://present5.com/presentation/777583256f3e4a245c0ee3b7918f1fbe/image-10.jpg" alt="Comparing to paired t-test > plot(Anova$coefficients[, "W"], Limma. PTT$coefficients) > plot(Anova$sigma, Limma. PTT$sigma) >" /> Comparing to paired t-test > plot(Anova$coefficients[, "W"], Limma. PTT$coefficients) > plot(Anova$sigma, Limma. PTT$sigma) > plot(Anova$stdev. unscaled[, "W"], Limma. PTT$stdev. unscaled) > plot(Anova$sigma*Anova$stdev. unscaled[, "W"], Limma. PTT$sigma*Limma. PTT$stdev. unscaled) > plot(Anova$df. residual, Limma. PTT$df. residual) 1 -20 -05 10

" src="https://present5.com/presentation/777583256f3e4a245c0ee3b7918f1fbe/image-11.jpg" alt="Adjusting for Dye - Three-way ANOVA > dye<-c(rep("Cy 5", 6), rep("Cy 3", 6)) >" /> Adjusting for Dye - Three-way ANOVA > dye<-c(rep("Cy 5", 6), rep("Cy 3", 6)) > > designad<-model. matrix(~-1+factor(array)+factor(dye)+factor(trt)) > #designad > colnames(designad)<-c(paste("A", 1: 6, sep=""), "Cy 5", "W") > designad A 1 A 2 A 3 A 4 A 5 A 6 Cy 5 W 1 1 0 0 0 11 2 0 1 0 0 10 3 0 0 1 0 0 0 11 4 0 0 0 10 5 0 0 1 0 11 6 0 0 0 1 10 7 1 0 0 00 8 0 1 0 0 01 9 0 0 1 0 00 10 0 1 0 0 0 1 11 0 0 0 12 0 0 0 1 attr(, "assign") [1] 1 1 1 2 3 attr(, "contrasts")$"factor(array)" [1] "contr. treatment" attr(, "contrasts")$"factor(dye)" [1] "contr. treatment" attr(, "contrasts")$"factor(trt)" [1] "contr. treatment" 1 -20 -05 11

Adjusting for Dye - Three-way ANOVA >Anovad<-lm. Fit(DAnova, designad) > > Anova$coefficients[2, ] A 1 A 2 A 3 A 4 A 5 A 6 W 8. 36197475 9. 90627295 11. 34002704 10. 77586480 9. 35096212 9. 92299117 -0. 03068036 > Limma. PTT$coefficients[2] [1] -0. 03068036 > Anovad$coefficients[2, ] A 1 A 2 A 3 A 4 A 5 A 6 Cy 5 W 8. 38440701 9. 92870520 11. 36245930 10. 79829705 9. 37339438 9. 94542342 -0. 04486451 -0. 03068036 > Anova$coefficients[1, ] A 1 A 2 A 3 A 4 A 5 A 6 W NA NA 6. 3898451 6. 3585492 6. 4163747 7. 0123661 0. 1875361 > Limma. PTT$coefficients[1] 0. 1875361 > Anovad$coefficients[1, ] A 1 A 2 A 3 A 4 A 5 A 6 Cy 5 W NA NA 6. 43844153 6. 40714571 6. 46497115 7. 06096259 -0. 09719295 0. 18753615 > 1 -20 -05 12

plot(Anovad$sigma, Limma. PTT$sigma) >" src="https://present5.com/presentation/777583256f3e4a245c0ee3b7918f1fbe/image-13.jpg" alt="Comparing to paired t-test > plot(Anovad$coefficients[, "W"], Limma. PTT$coefficients) > plot(Anovad$sigma, Limma. PTT$sigma) >" /> Comparing to paired t-test > plot(Anovad$coefficients[, "W"], Limma. PTT$coefficients) > plot(Anovad$sigma, Limma. PTT$sigma) > plot(Anovad$stdev. unscaled[, "W"], Limma. PTT$stdev. unscaled) > plot(Anovad$sigma*Anova$stdev. unscaled[, "W"], Limma. PTT$sigma*Limma. PTT$stdev. unscaled) > plot(Anovad$df. residual, Limma. PTT$df. residual) 1 -20 -05 13

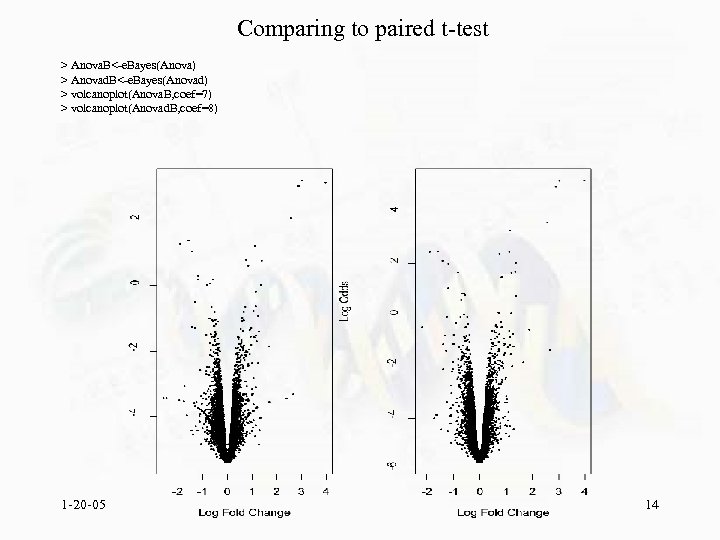Comparing to paired t-test > Anova. B<-e. Bayes(Anova) > Anovad. B<-e. Bayes(Anovad) > volcanoplot(Anova. B, coef=7) > volcanoplot(Anovad. B, coef=8) 1 -20 -05 14