c8f055263859bbe3f2111f03f15df4d2.ppt
- Количество слайдов: 48
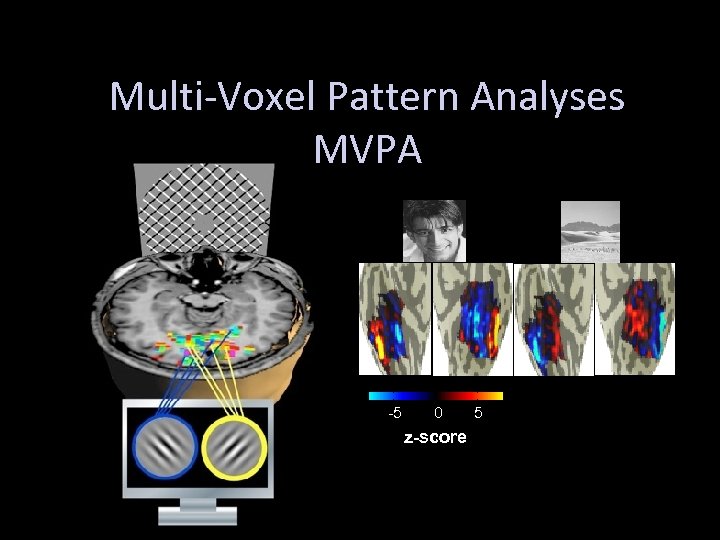 Multi-Voxel Pattern Analyses MVPA -5 0 z-score 5
Multi-Voxel Pattern Analyses MVPA -5 0 z-score 5
 What Information Can You Infer from Multivoxel Patterns (MVP)?
What Information Can You Infer from Multivoxel Patterns (MVP)?
 What Information Can You Infer from Multivoxel Patterns (MVP)? • In traditional f. MRI analyses, we average across the voxels within an area, but what if the voxels are not homogeneous in their response properties? Distributed activations across voxels may contain valuable information.
What Information Can You Infer from Multivoxel Patterns (MVP)? • In traditional f. MRI analyses, we average across the voxels within an area, but what if the voxels are not homogeneous in their response properties? Distributed activations across voxels may contain valuable information.
 What Information Can You Infer from Multivoxel Patterns (MVP)? • In traditional f. MRI analyses, we average across the voxels within an area, but what if the voxels are not homogeneous in their response properties? Distributed activations across voxels may contain valuable information. • In traditional f. MRI analyses, we assume that an area encodes a stimulus if it responds more to it than others. However, encoding may depend on the distributed pattern of both high and low activations.
What Information Can You Infer from Multivoxel Patterns (MVP)? • In traditional f. MRI analyses, we average across the voxels within an area, but what if the voxels are not homogeneous in their response properties? Distributed activations across voxels may contain valuable information. • In traditional f. MRI analyses, we assume that an area encodes a stimulus if it responds more to it than others. However, encoding may depend on the distributed pattern of both high and low activations.
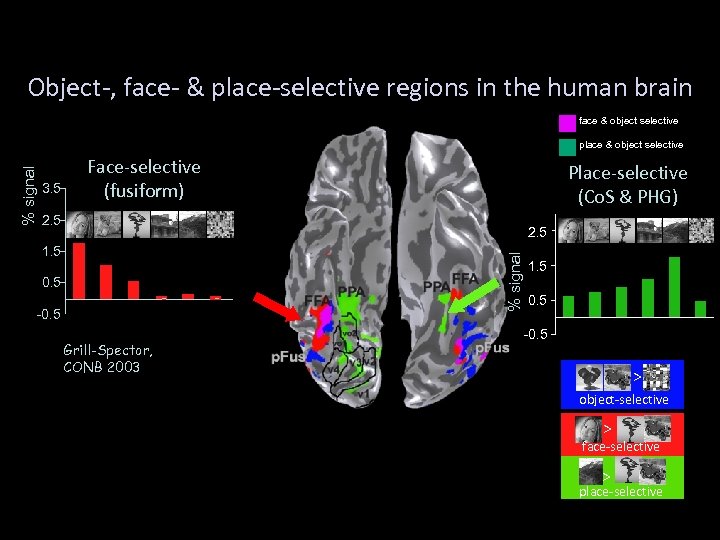 Object-, face- & place-selective regions in the human brain face & object selective 3. 5 Face-selective (fusiform) Place-selective (Co. S & PHG) 2. 5 1. 5 0. 5 FUS houses -0. 5 houses % signal place & object selective 1. 5 FUS 0. 5 faces Grill-Spector, CONB 2003 animals novel houses -0. 5 > object-selective > lateral view face-selective > lateral view place-selective emptyscene text
Object-, face- & place-selective regions in the human brain face & object selective 3. 5 Face-selective (fusiform) Place-selective (Co. S & PHG) 2. 5 1. 5 0. 5 FUS houses -0. 5 houses % signal place & object selective 1. 5 FUS 0. 5 faces Grill-Spector, CONB 2003 animals novel houses -0. 5 > object-selective > lateral view face-selective > lateral view place-selective emptyscene text
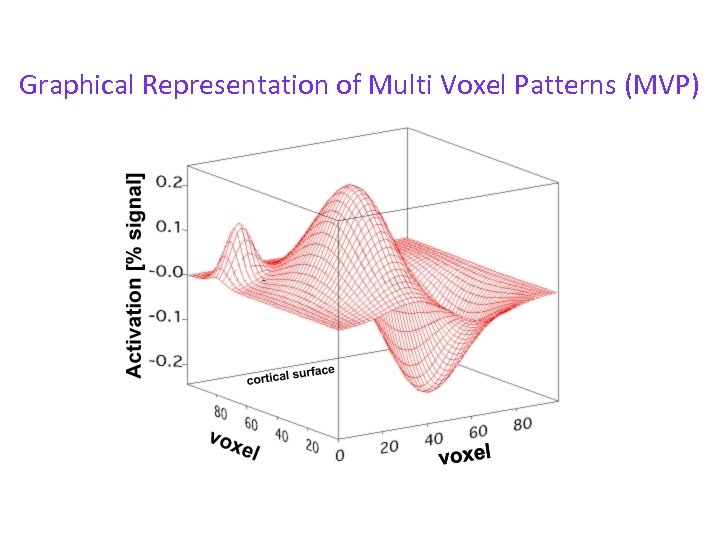 Graphical Representation of Multi Voxel Patterns (MVP)
Graphical Representation of Multi Voxel Patterns (MVP)
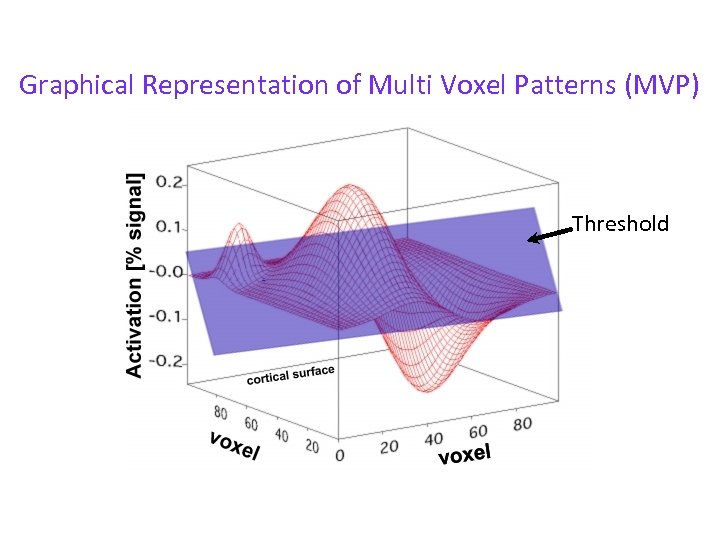 Graphical Representation of Multi Voxel Patterns (MVP) Threshold
Graphical Representation of Multi Voxel Patterns (MVP) Threshold
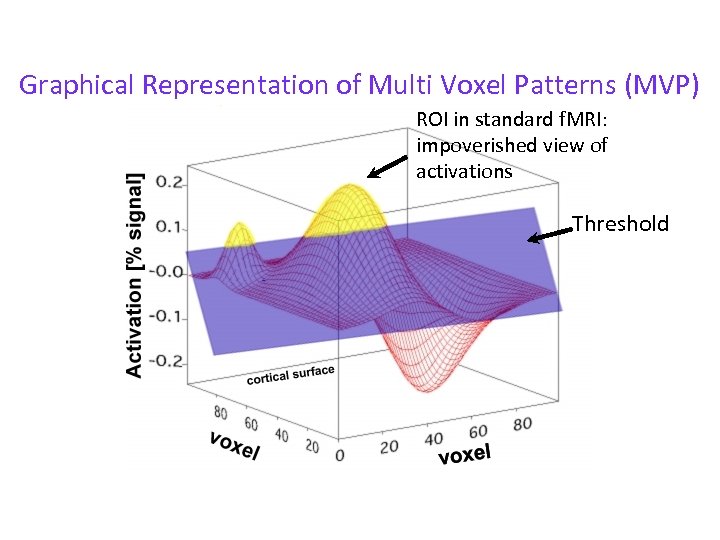 Graphical Representation of Multi Voxel Patterns (MVP) ROI in standard f. MRI: impoverished view of activations Threshold
Graphical Representation of Multi Voxel Patterns (MVP) ROI in standard f. MRI: impoverished view of activations Threshold
 Problem: Is there an area in the brain for every object category? Hypothesis: Distributed activation patterns across the ventral stream (rather than areas) code object categories. Haxby et al. Science 2001
Problem: Is there an area in the brain for every object category? Hypothesis: Distributed activation patterns across the ventral stream (rather than areas) code object categories. Haxby et al. Science 2001
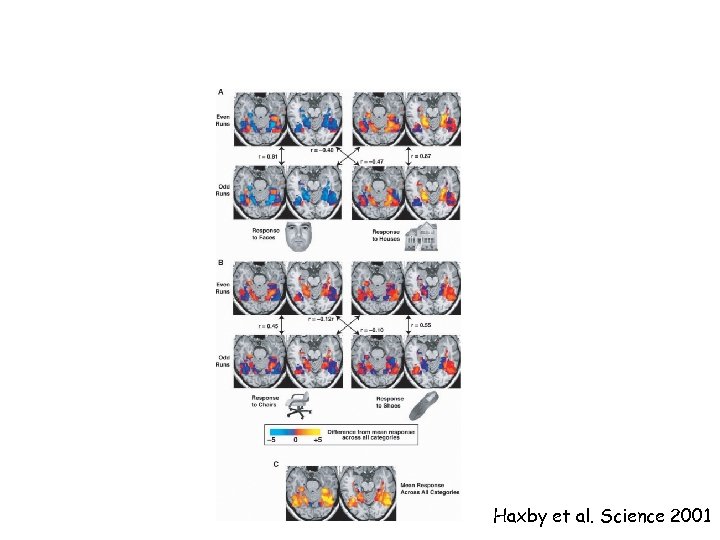 Haxby et al. Science 2001
Haxby et al. Science 2001
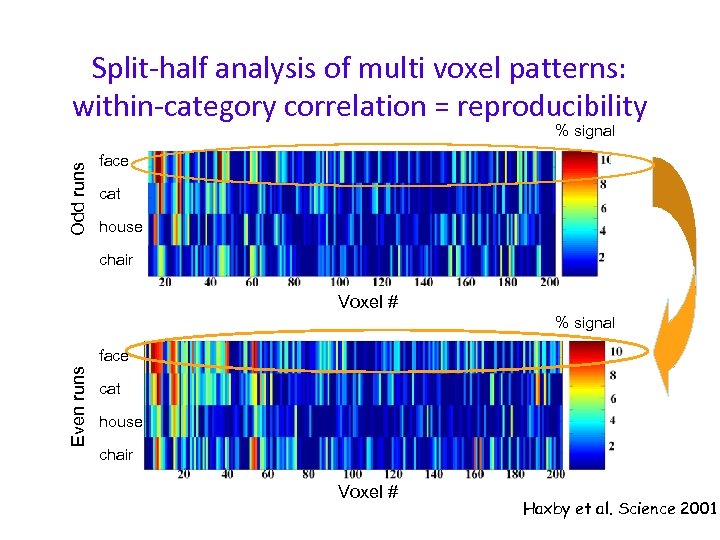 Split-half analysis of multi voxel patterns: within-category correlation = reproducibility Odd runs % signal face cat house chair Voxel # % signal Even runs face cat house chair Voxel # Haxby et al. Science 2001
Split-half analysis of multi voxel patterns: within-category correlation = reproducibility Odd runs % signal face cat house chair Voxel # % signal Even runs face cat house chair Voxel # Haxby et al. Science 2001
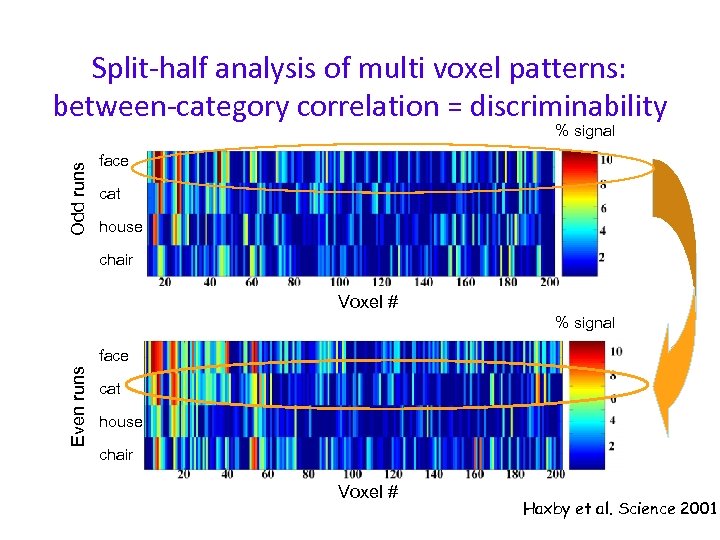 Split-half analysis of multi voxel patterns: between-category correlation = discriminability Odd runs % signal face cat house chair Voxel # % signal Even runs face cat house chair Voxel # Haxby et al. Science 2001
Split-half analysis of multi voxel patterns: between-category correlation = discriminability Odd runs % signal face cat house chair Voxel # % signal Even runs face cat house chair Voxel # Haxby et al. Science 2001
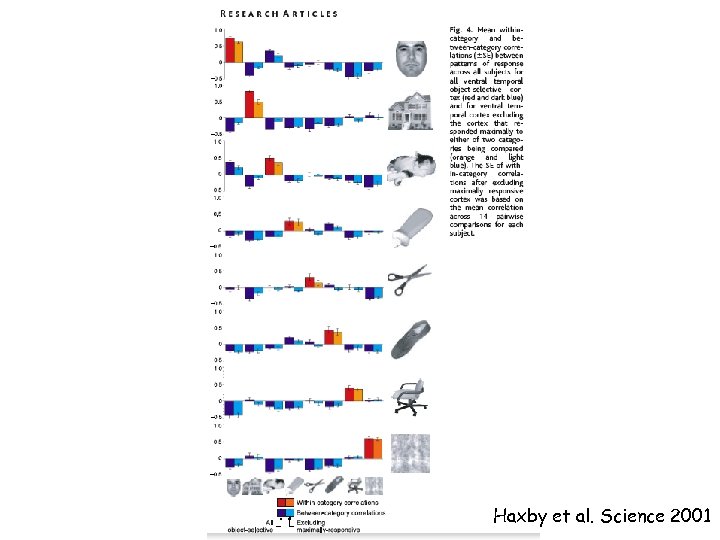 Haxby et al. Science 2001
Haxby et al. Science 2001
 Simple Correlation Analysis • Measure within-category correlations – within faces (F 1: F 2) – within cats (C 1: C 2) • Measure between-category correlations – Between faces: cats (F 1: C 2; F 2: C 1) • If within-category correlations > between-category correlations, conclude that area encodes different stimuli face cat house chair
Simple Correlation Analysis • Measure within-category correlations – within faces (F 1: F 2) – within cats (C 1: C 2) • Measure between-category correlations – Between faces: cats (F 1: C 2; F 2: C 1) • If within-category correlations > between-category correlations, conclude that area encodes different stimuli face cat house chair
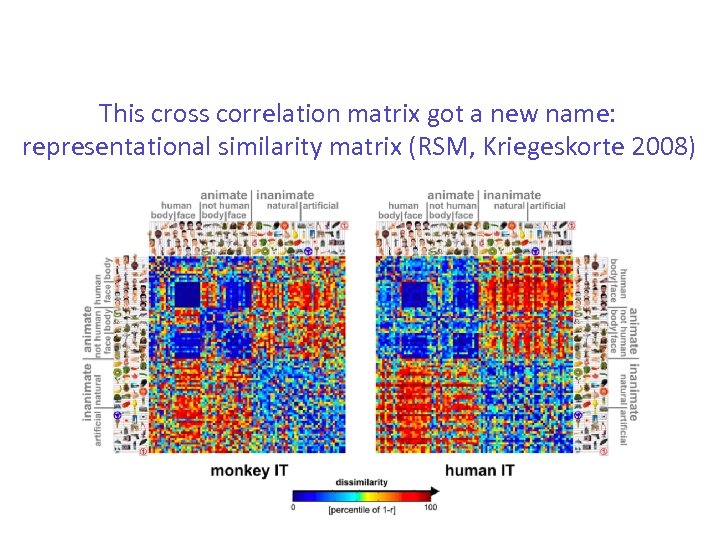 This cross correlation matrix got a new name: representational similarity matrix (RSM, Kriegeskorte 2008)
This cross correlation matrix got a new name: representational similarity matrix (RSM, Kriegeskorte 2008)
 What values do you include to represent multivoxel patterns? • • Beta values/raw amplitudes Subtracted betas T-values Z-scores
What values do you include to represent multivoxel patterns? • • Beta values/raw amplitudes Subtracted betas T-values Z-scores
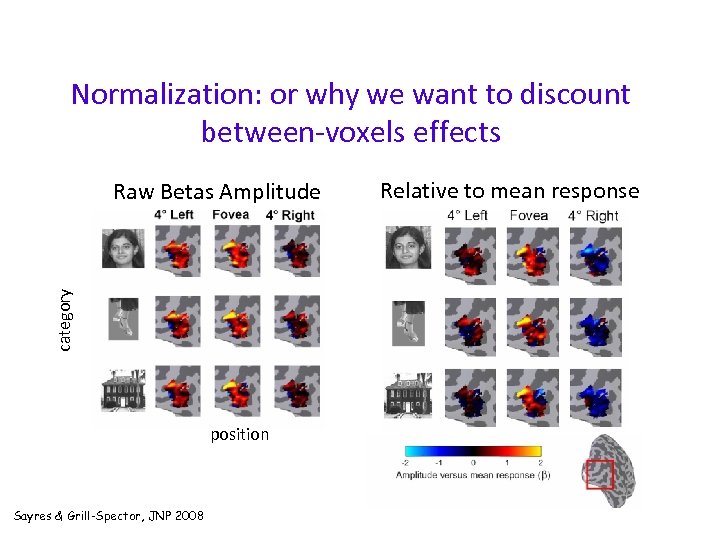 Normalization: or why we want to discount between-voxels effects category Raw Betas Amplitude position Sayres & Grill-Spector, JNP 2008 Relative to mean response
Normalization: or why we want to discount between-voxels effects category Raw Betas Amplitude position Sayres & Grill-Spector, JNP 2008 Relative to mean response
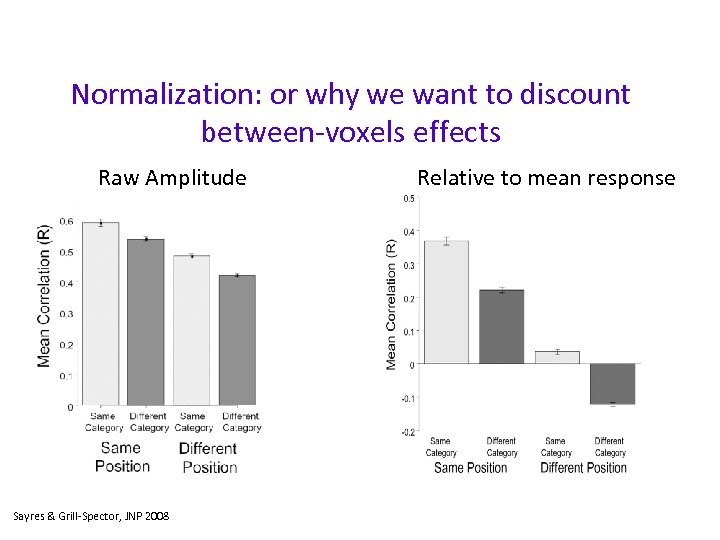 Normalization: or why we want to discount between-voxels effects Raw Amplitude Sayres & Grill-Spector, JNP 2008 Relative to mean response
Normalization: or why we want to discount between-voxels effects Raw Amplitude Sayres & Grill-Spector, JNP 2008 Relative to mean response
 Decoding: Can you classify what category the subject saw from brain MVPs?
Decoding: Can you classify what category the subject saw from brain MVPs?
 Classification • Training set: example multivoxel patterns (vectors which dimensionality is the number of voxels) that are labeled to classes.
Classification • Training set: example multivoxel patterns (vectors which dimensionality is the number of voxels) that are labeled to classes.
 Classification • Training set: example multivoxel patterns (vectors which dimensionality is the number of voxels) that are labeled to classes. • Find a rule that separates the classes
Classification • Training set: example multivoxel patterns (vectors which dimensionality is the number of voxels) that are labeled to classes. • Find a rule that separates the classes
 Classification • Training set: example multivoxel patterns (vectors which dimensionality is the number of voxels) that are labeled to classes. • Find a rule that separates the classes • Testing set: new multivoxel patterns. For each pattern determine to which class it belongs
Classification • Training set: example multivoxel patterns (vectors which dimensionality is the number of voxels) that are labeled to classes. • Find a rule that separates the classes • Testing set: new multivoxel patterns. For each pattern determine to which class it belongs
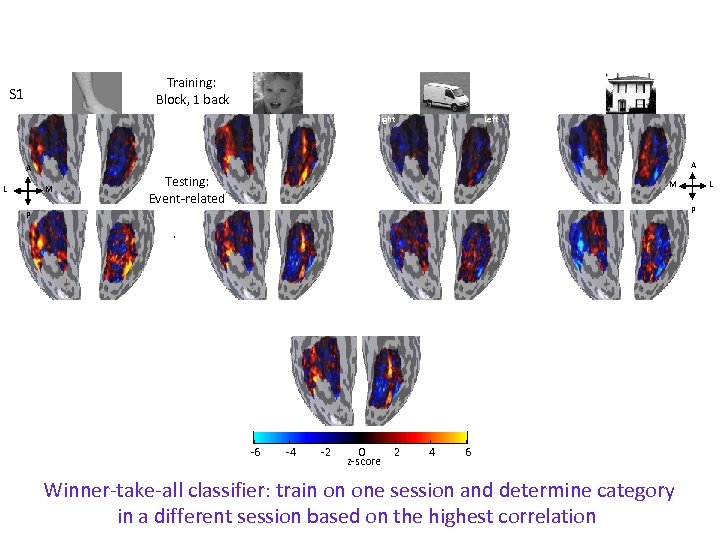 Training: Block, 1 back S 1 Right A A L Left M Testing: Event-related M L P P -6 -4 -2 0 z-score 2 4 6 Winner-take-all classifier: train on one session and determine category in a different session based on the highest correlation
Training: Block, 1 back S 1 Right A A L Left M Testing: Event-related M L P P -6 -4 -2 0 z-score 2 4 6 Winner-take-all classifier: train on one session and determine category in a different session based on the highest correlation
![Classifier [% correct] Winner-take-all classifier successfully decodes object category from distributed responses across ventral Classifier [% correct] Winner-take-all classifier successfully decodes object category from distributed responses across ventral](https://present5.com/presentation/c8f055263859bbe3f2111f03f15df4d2/image-24.jpg) Classifier [% correct] Winner-take-all classifier successfully decodes object category from distributed responses across ventral stream, but not for V 1 or control ROI 100 (n=7) 80 * 60 * * Anatomical VTC Control ROI * OTS 40 20 chance level 0 Control ROI V 1 Lateral VTC Co. S Medial VTC Medial Lateral Whole VTC VTC * significantly > chance, P < 0. 05 Weiner & Grill-Spector, Neuro. Image 2010
Classifier [% correct] Winner-take-all classifier successfully decodes object category from distributed responses across ventral stream, but not for V 1 or control ROI 100 (n=7) 80 * 60 * * Anatomical VTC Control ROI * OTS 40 20 chance level 0 Control ROI V 1 Lateral VTC Co. S Medial VTC Medial Lateral Whole VTC VTC * significantly > chance, P < 0. 05 Weiner & Grill-Spector, Neuro. Image 2010
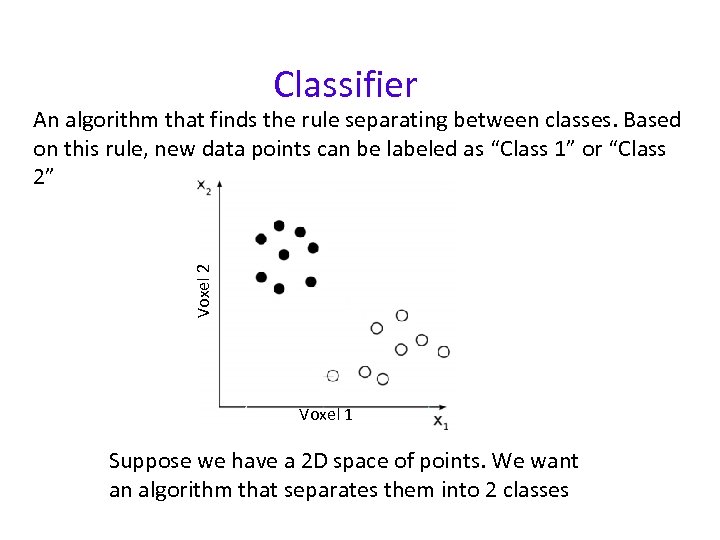 Classifier Voxel 2 An algorithm that finds the rule separating between classes. Based on this rule, new data points can be labeled as “Class 1” or “Class 2” Voxel 1 Suppose we have a 2 D space of points. We want an algorithm that separates them into 2 classes
Classifier Voxel 2 An algorithm that finds the rule separating between classes. Based on this rule, new data points can be labeled as “Class 1” or “Class 2” Voxel 1 Suppose we have a 2 D space of points. We want an algorithm that separates them into 2 classes
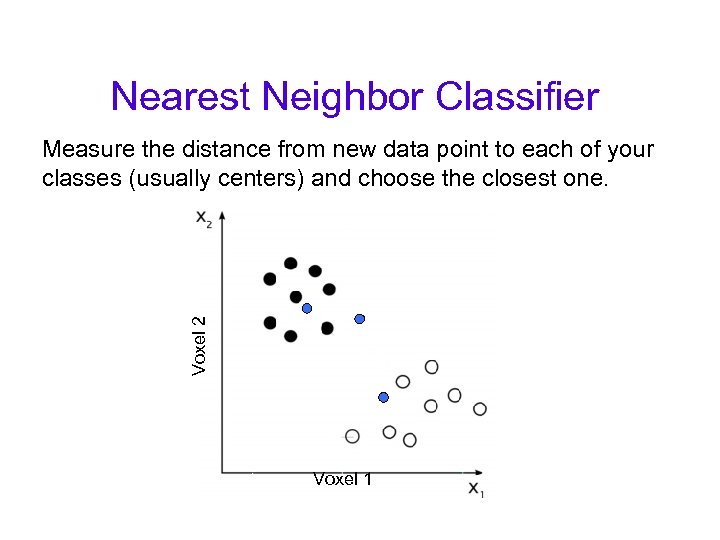 Nearest Neighbor Classifier Voxel 2 Measure the distance from new data point to each of your classes (usually centers) and choose the closest one. Voxel 1
Nearest Neighbor Classifier Voxel 2 Measure the distance from new data point to each of your classes (usually centers) and choose the closest one. Voxel 1
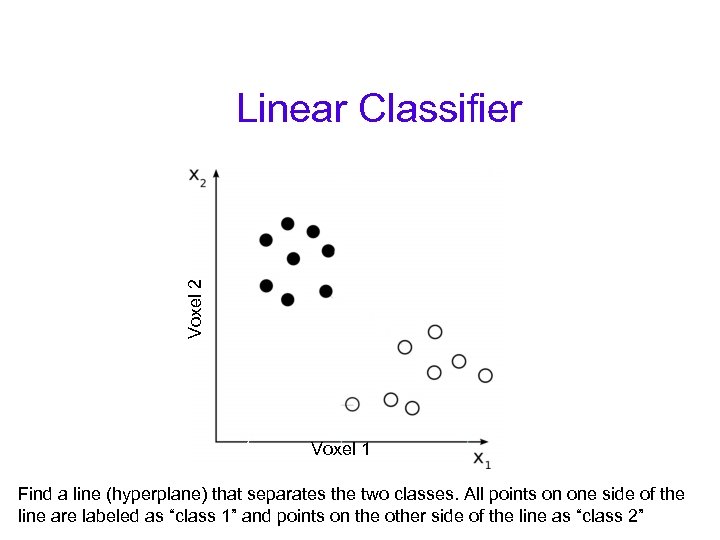 Voxel 2 Linear Classifier Voxel 1 Find a line (hyperplane) that separates the two classes. All points on one side of the line are labeled as “class 1” and points on the other side of the line as “class 2”
Voxel 2 Linear Classifier Voxel 1 Find a line (hyperplane) that separates the two classes. All points on one side of the line are labeled as “class 1” and points on the other side of the line as “class 2”
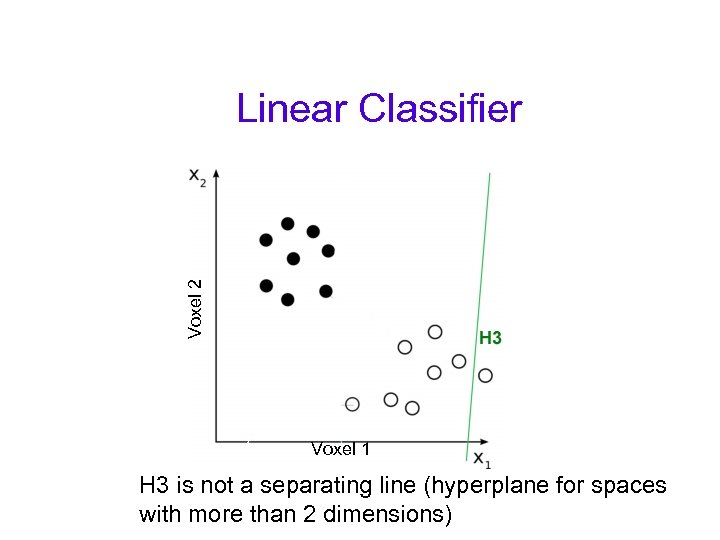 Voxel 2 Linear Classifier Voxel 1 H 3 is not a separating line (hyperplane for spaces with more than 2 dimensions)
Voxel 2 Linear Classifier Voxel 1 H 3 is not a separating line (hyperplane for spaces with more than 2 dimensions)
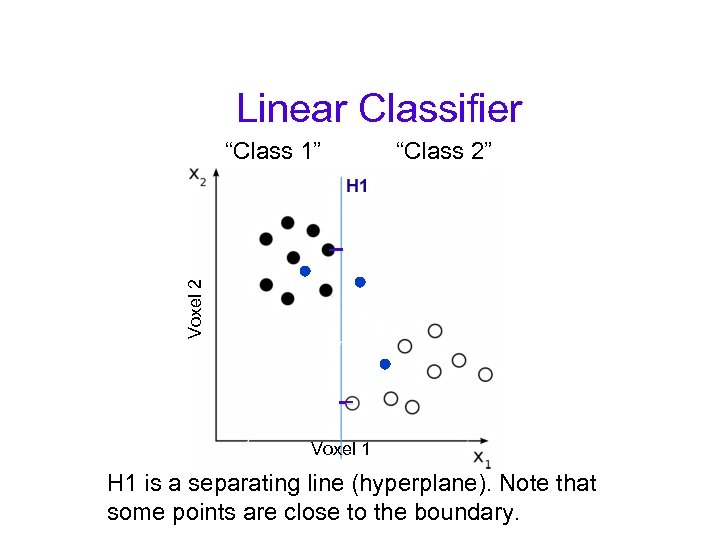 Linear Classifier “Class 2” Voxel 2 “Class 1” Voxel 1 H 1 is a separating line (hyperplane). Note that some points are close to the boundary.
Linear Classifier “Class 2” Voxel 2 “Class 1” Voxel 1 H 1 is a separating line (hyperplane). Note that some points are close to the boundary.
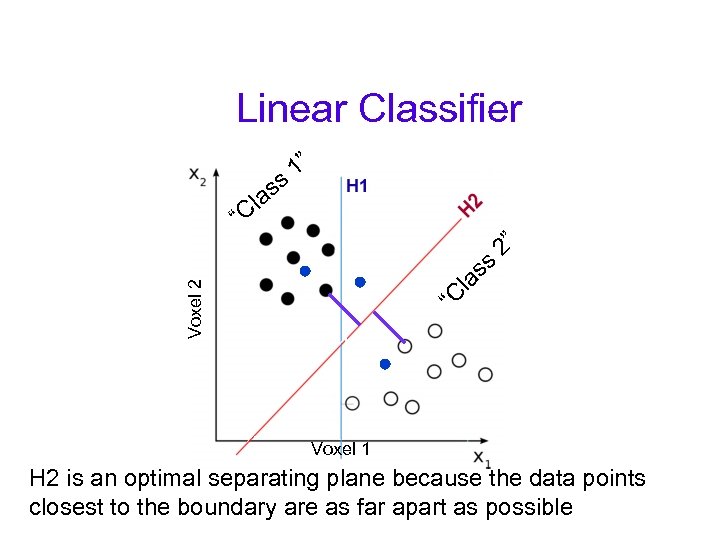 Linear Classifier “C Voxel 2 la ss 2” “ ss la C 1” Voxel 1 H 2 is an optimal separating plane because the data points closest to the boundary are as far apart as possible
Linear Classifier “C Voxel 2 la ss 2” “ ss la C 1” Voxel 1 H 2 is an optimal separating plane because the data points closest to the boundary are as far apart as possible
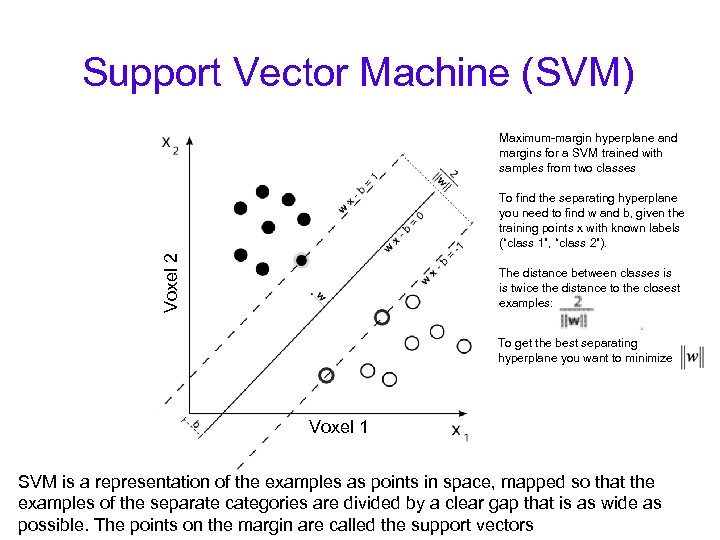 Support Vector Machine (SVM) Maximum-margin hyperplane and margins for a SVM trained with samples from two classes Voxel 2 To find the separating hyperplane you need to find w and b, given the training points x with known labels (“class 1”, “class 2”). The distance between classes is is twice the distance to the closest examples: To get the best separating hyperplane you want to minimize Voxel 1 SVM is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. The points on the margin are called the support vectors
Support Vector Machine (SVM) Maximum-margin hyperplane and margins for a SVM trained with samples from two classes Voxel 2 To find the separating hyperplane you need to find w and b, given the training points x with known labels (“class 1”, “class 2”). The distance between classes is is twice the distance to the closest examples: To get the best separating hyperplane you want to minimize Voxel 1 SVM is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. The points on the margin are called the support vectors
 Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification.
Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification.
 Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • sup
Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • sup
 Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. sup
Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. sup
 Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. • New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall on. The separating plane between the two categories is called a hyperplane. • sup
Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. • New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall on. The separating plane between the two categories is called a hyperplane. • sup
 Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. • New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall on. The separating plane between the two categories is called a hyperplane. • Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training datapoints of any class (socalled functional margin), since in general the larger the margin the lower the generalization error of the classifier. • Training samples on the margin are called the support vectors.
Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. • New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall on. The separating plane between the two categories is called a hyperplane. • Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training datapoints of any class (socalled functional margin), since in general the larger the margin the lower the generalization error of the classifier. • Training samples on the margin are called the support vectors.
 Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. • New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall on. The separating plane between the two categories is called a hyperplane. • Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training datapoints of any class (socalled functional margin), since in general the larger the margin the lower the generalization error of the classifier. • Training samples on the margin are called the support vectors.
Support Vector Machine (SVM) • Support vector machines (SVMs) are a set of supervised learning methods used for classification. • Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that predicts whether a new example falls into one category or the other. • An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. • New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall on. The separating plane between the two categories is called a hyperplane. • Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training datapoints of any class (socalled functional margin), since in general the larger the margin the lower the generalization error of the classifier. • Training samples on the margin are called the support vectors.
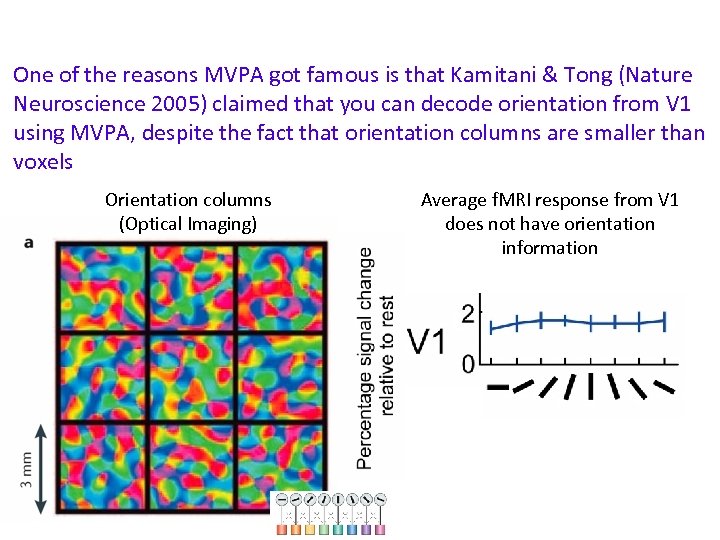 One of the reasons MVPA got famous is that Kamitani & Tong (Nature Neuroscience 2005) claimed that you can decode orientation from V 1 using MVPA, despite the fact that orientation columns are smaller than voxels Orientation columns (Optical Imaging) Average f. MRI response from V 1 does not have orientation information
One of the reasons MVPA got famous is that Kamitani & Tong (Nature Neuroscience 2005) claimed that you can decode orientation from V 1 using MVPA, despite the fact that orientation columns are smaller than voxels Orientation columns (Optical Imaging) Average f. MRI response from V 1 does not have orientation information
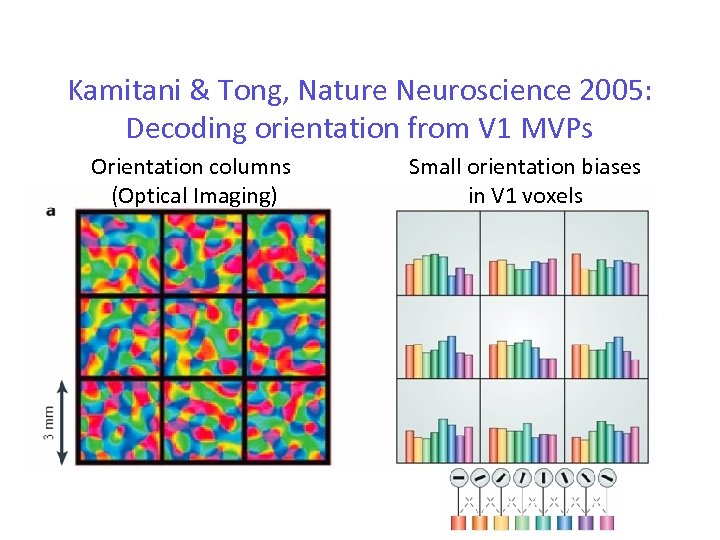 Kamitani & Tong, Nature Neuroscience 2005: Decoding orientation from V 1 MVPs Orientation columns (Optical Imaging) Small orientation biases in V 1 voxels
Kamitani & Tong, Nature Neuroscience 2005: Decoding orientation from V 1 MVPs Orientation columns (Optical Imaging) Small orientation biases in V 1 voxels
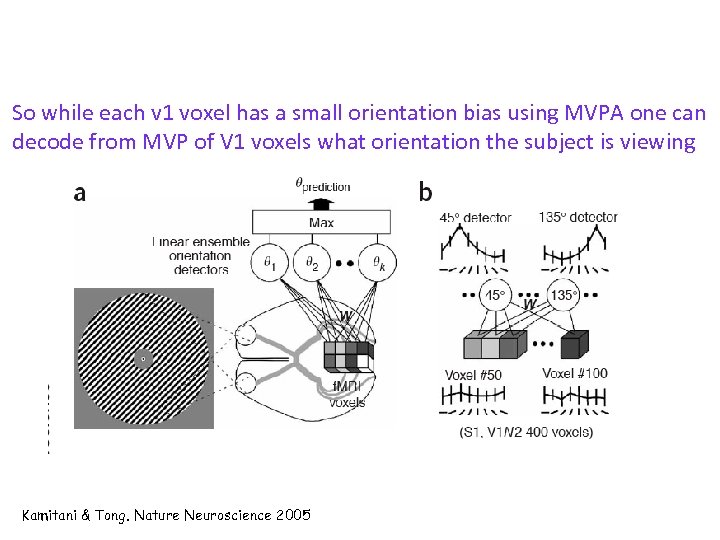 So while each v 1 voxel has a small orientation bias using MVPA one can decode from MVP of V 1 voxels what orientation the subject is viewing Kamitani & Tong. Nature Neuroscience 2005
So while each v 1 voxel has a small orientation bias using MVPA one can decode from MVP of V 1 voxels what orientation the subject is viewing Kamitani & Tong. Nature Neuroscience 2005
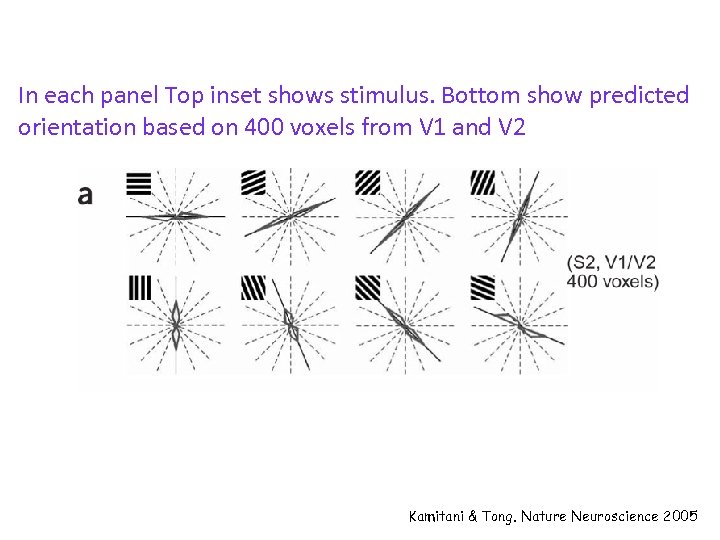 In each panel Top inset shows stimulus. Bottom show predicted orientation based on 400 voxels from V 1 and V 2 Kamitani & Tong. Nature Neuroscience 2005
In each panel Top inset shows stimulus. Bottom show predicted orientation based on 400 voxels from V 1 and V 2 Kamitani & Tong. Nature Neuroscience 2005
 Orientation and angular-position topographic maps for a single subject shown on a flattened representation of the occipital lobe. However, Jeremy Freemen, David Heeger and Elias Miriam are pushing back on the interpretation that MVPA gives you subvoxel resolution. In fact they show that what is being picked up in MVPA is between voxel patterns (or maps) rather than within voxel biases Freeman J et al. J. Neurosci. 2011; 31: 4792 -4804 © 2011 by Society for Neuroscience
Orientation and angular-position topographic maps for a single subject shown on a flattened representation of the occipital lobe. However, Jeremy Freemen, David Heeger and Elias Miriam are pushing back on the interpretation that MVPA gives you subvoxel resolution. In fact they show that what is being picked up in MVPA is between voxel patterns (or maps) rather than within voxel biases Freeman J et al. J. Neurosci. 2011; 31: 4792 -4804 © 2011 by Society for Neuroscience
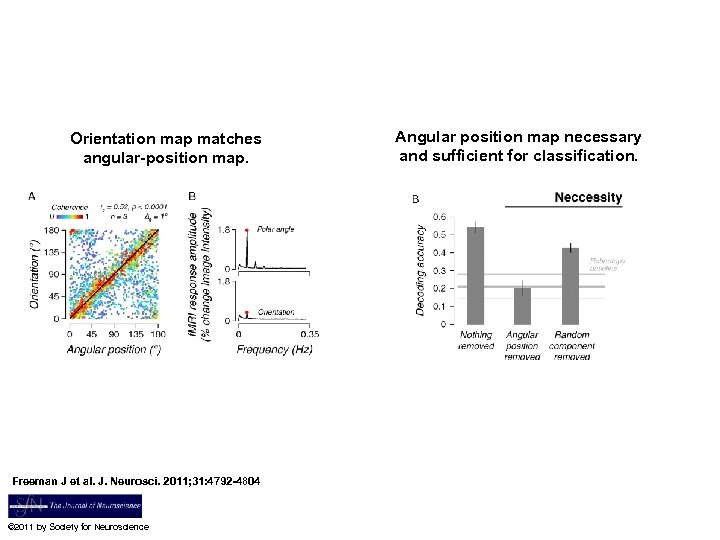 Orientation map matches angular-position map. Freeman J et al. J. Neurosci. 2011; 31: 4792 -4804 © 2011 by Society for Neuroscience Angular position map necessary and sufficient for classification.
Orientation map matches angular-position map. Freeman J et al. J. Neurosci. 2011; 31: 4792 -4804 © 2011 by Society for Neuroscience Angular position map necessary and sufficient for classification.
 Limitations of decoding MVPs • Limited by voxels “biases” at the resolution you measure – These biases need to be reproducible
Limitations of decoding MVPs • Limited by voxels “biases” at the resolution you measure – These biases need to be reproducible
 Limitations of decoding MVPs • Limited by voxels “biases” at the resolution you measure – These biases need to be reproducible • Useful for applications like prosthetics, mind reading, but does it tell us how the brain works? – Need generative/encoding models of the brain (e. g. , Kay et al, Nature, 2008)
Limitations of decoding MVPs • Limited by voxels “biases” at the resolution you measure – These biases need to be reproducible • Useful for applications like prosthetics, mind reading, but does it tell us how the brain works? – Need generative/encoding models of the brain (e. g. , Kay et al, Nature, 2008)
 Limitations of decoding MVPs • Limited by voxels “biases” at the resolution you measure – These biases need to be reproducible • Useful for applications like prosthetics, mind reading, but does it tell us how the brain works? – Need generative/encoding models of the brain (e. g. , Kay et al, Nature, 2008) • A brain area may contain distributed information, but the brain may not use this information as a classifier does? – In other words, does the brain operate like a classifier? SVM? What about non-linear classifiers?
Limitations of decoding MVPs • Limited by voxels “biases” at the resolution you measure – These biases need to be reproducible • Useful for applications like prosthetics, mind reading, but does it tell us how the brain works? – Need generative/encoding models of the brain (e. g. , Kay et al, Nature, 2008) • A brain area may contain distributed information, but the brain may not use this information as a classifier does? – In other words, does the brain operate like a classifier? SVM? What about non-linear classifiers?
 Neural responses to visual scenes reveals inconsistencies between f. MRI adaptation and multivoxel pattern analysis. Epstein RA, Morgan LK. Neuropsychologia. 2012 Mar; 50(4): 530 -43.
Neural responses to visual scenes reveals inconsistencies between f. MRI adaptation and multivoxel pattern analysis. Epstein RA, Morgan LK. Neuropsychologia. 2012 Mar; 50(4): 530 -43.
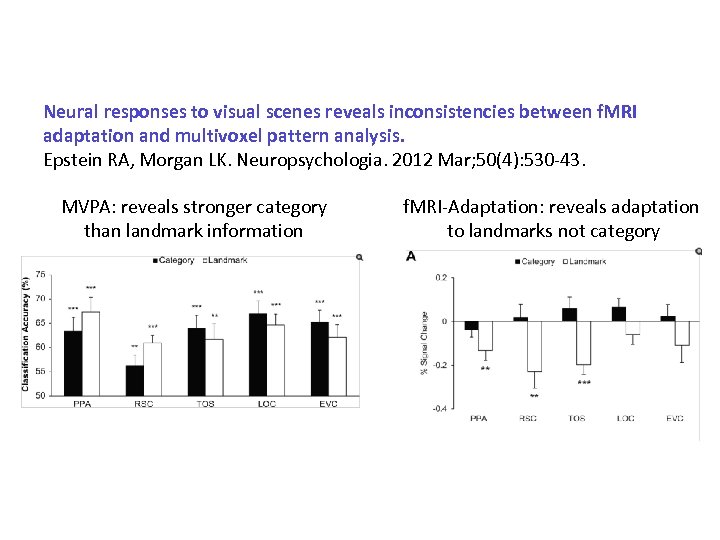 Neural responses to visual scenes reveals inconsistencies between f. MRI adaptation and multivoxel pattern analysis. Epstein RA, Morgan LK. Neuropsychologia. 2012 Mar; 50(4): 530 -43. MVPA: reveals stronger category than landmark information f. MRI-Adaptation: reveals adaptation to landmarks not category
Neural responses to visual scenes reveals inconsistencies between f. MRI adaptation and multivoxel pattern analysis. Epstein RA, Morgan LK. Neuropsychologia. 2012 Mar; 50(4): 530 -43. MVPA: reveals stronger category than landmark information f. MRI-Adaptation: reveals adaptation to landmarks not category


