Multi Layer Perceptron Threshold Logic Unit TLU

Multi Layer Perceptron

Threshold Logic Unit (TLU) inputs x 1 x 2 . . . xn w 1 w 2 wn weights output activation a= i=1 n wi xi y= { q 1 if a q 0 if a < q y

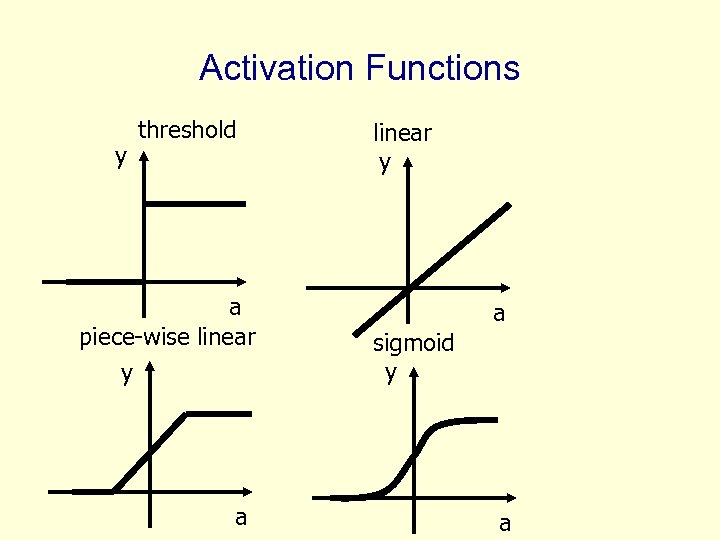Activation Functions y threshold a piece-wise linear y a sigmoid y a

Decision Surface of a TLU 1 w 1 x 2 1 Decision line w 1 x 1 + w 2 x 2 = q 0 0 0 1 0 0 x 1

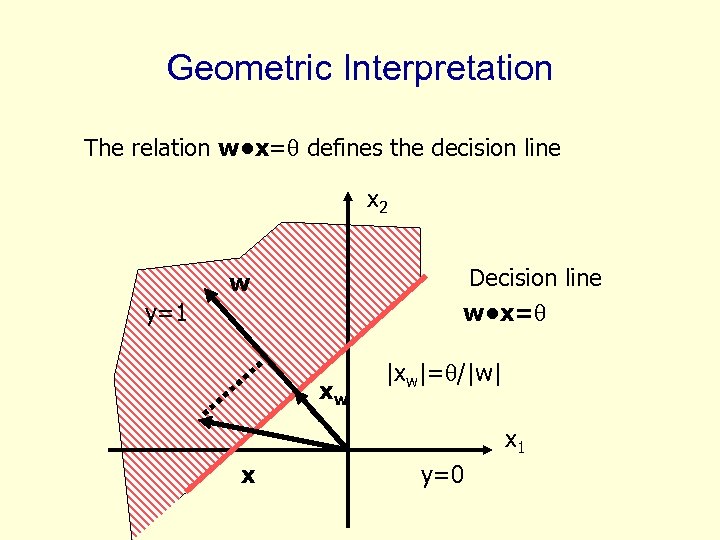Geometric Interpretation The relation w • x=q defines the decision line x 2 Decision line w • x=q w y=1 xw |xw|=q/|w| x 1 x y=0

Geometric Interpretation • In n dimensions the relation w • x=q defines a n 1 dimensional hyper-plane, which is perpendicular to the weight vector w. • On one side of the hyper-plane (w • x>q) all patterns are classified by the TLU as “ 1”, while those that get classified as “ 0” lie on the other side of the hyperplane. • If patterns can be not separated by a hyper-plane then they cannot be correctly classified with a TLU.

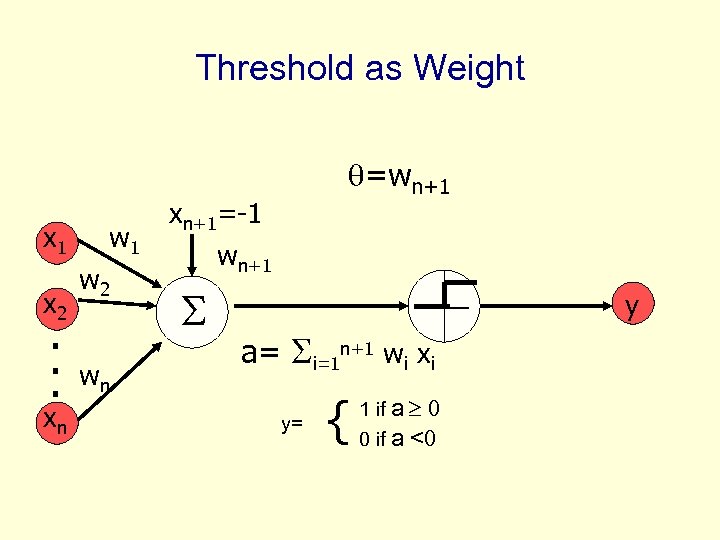Threshold as Weight x 1 x 2 . . . xn w 1 w 2 wn q=wn+1 xn+1=-1 wn+1 y a= i=1 n+1 wi xi y= { 1 if a 0 0 if a <0

Training ANNs • Training set S of examples {x, t} – x is an input vector and – t the desired target vector – Example: Logical And S = {(0, 0), 0}, {(0, 1), 0}, {(1, 0), 0}, {(1, 1), 1} • Iterative process – Present a training example x , compute network output y , compare output y with target t, adjust weights and thresholds • Learning rule – Specifies how to change the weights w and thresholds q of the network as a function of the inputs x, output y and target t.

Perceptron Learning Rule • w’=w + (t-y) x Or in components • w’i = wi + wi = wi + (t-y) xi (i=1. . n+1) With wn+1 = q and xn+1=-1 • The parameter is called the learning rate. It determines the magnitude of weight updates wi. • If the output is correct (t=y) the weights are not changed ( wi =0). • If the output is incorrect (t y) the weights wi are changed such that the output of the TLU for the new weights w’i is closer/further to the input xi.

Perceptron Training Algorithm Repeat for each training vector pair (x, t) evaluate the output y when x is the input if y t then form a new weight vector w’ according to w’=w + (t-y) x else do nothing end if end for Until y=t for all training vector pairs

Perceptron Convergence Theorem The algorithm converges to the correct classification – if the training data is linearly separable – and is sufficiently small • If two classes of vectors X 1 and X 2 are linearly separable, the application of the perceptron training algorithm will eventually result in a weight vector w 0, such that w 0 defines a TLU whose decision hyper-plane separates X 1 and X 2 (Rosenblatt 1962). • Solution w 0 is not unique, since if w 0 x =0 defines a hyper-plane, so does w’ 0 = k w 0.

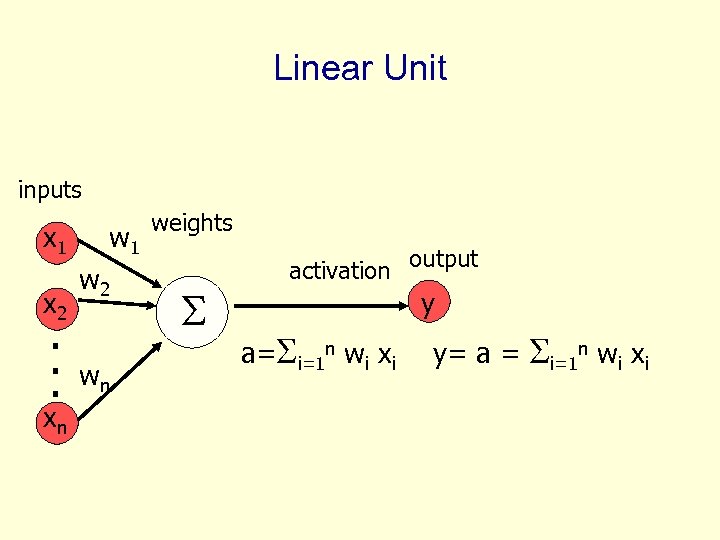Linear Unit inputs x 1 x 2 . . . xn w 1 w 2 wn weights activation output y a= i=1 n wi xi y= a = i=1 n wi xi

Gradient Descent Learning Rule • Consider linear unit without threshold and continuous output o (not just – 1, 1) – o=w 0 + w 1 x 1 + … + wn xn • Train the wi’s such that they minimize the squared error – E[w 1, …, wn] = ½ d D (td-od)2 where D is the set of training examples

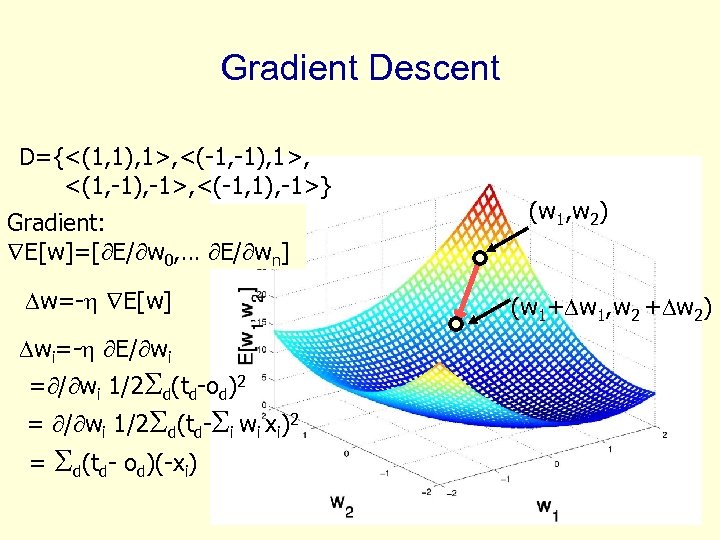Gradient Descent D={<(1, 1), 1>, <(-1, -1), 1>, <(1, -1), -1>, <(-1, 1), -1>} Gradient: E[w]=[ E/ w 0, … E/ wn] w=- E[w] wi=- E/ wi = / wi 1/2 d(td-od)2 = / wi 1/2 d(td- i wi xi)2 = d(td- od)(-xi) (w 1, w 2) (w 1+ w 1, w 2 + w 2)

Incremental Stochastic Gradient Descent • Batch mode : gradient descent w=w - ED[w] over the entire data D ED[w]=1/2 d(td-od)2 • Incremental mode: gradient descent w=w - Ed[w] over individual training examples d Ed[w]=1/2 (td-od)2 Incremental Gradient Descent can approximate Batch Gradient Descent arbitrarily closely if is small enough

Perceptron vs. Gradient Descent Rule • perceptron rule w’i = wi + (tp-yp) xip derived from manipulation of decision surface. • gradient descent rule w’i = wi + (tp-yp) xip derived from minimization of error function E[w 1, …, wn] = ½ p (tp-yp)2 by means of gradient descent. Where is the big difference?

Perceptron vs. Gradient Descent Rule Perceptron learning rule guaranteed to succeed if • Training examples are linearly separable • Sufficiently small learning rate Linear unit training rules uses gradient descent • Guaranteed to converge to hypothesis with minimum squared error • Given sufficiently small learning rate • Even when training data contains noise • Even when training data not separable by H

Presentation of Training Examples • Presenting all training examples once to the ANN is called an epoch. • In incremental stochastic gradient descent training examples can be presented in – Fixed order (1, 2, 3…, M) – Randomly permutated order (5, 2, 7, …, 3) – Completely random (4, 1, 7, 1, 5, 4, ……)

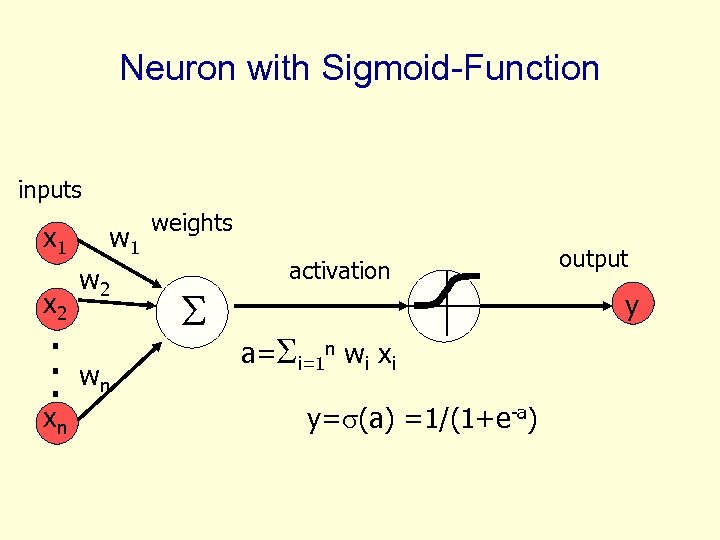Neuron with Sigmoid-Function inputs x 1 x 2 . . . xn w 1 w 2 wn weights activation output y a= i=1 n wi xi y= (a) =1/(1+e-a)

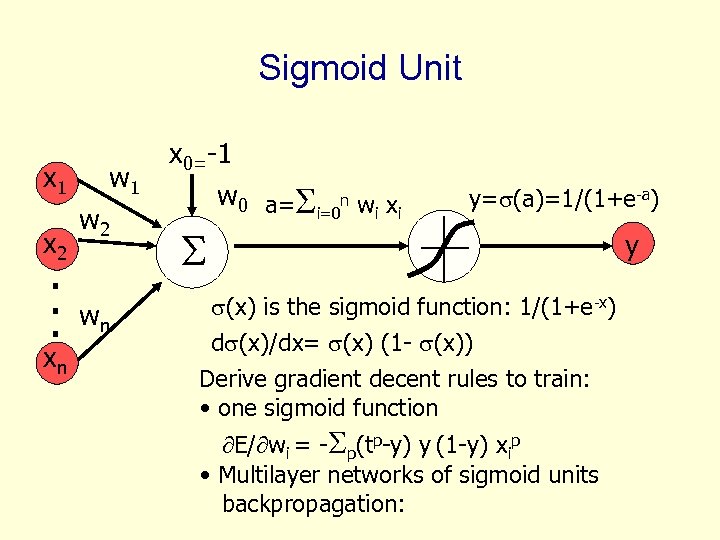Sigmoid Unit x 1 x 2 . . . xn w 1 w 2 wn x 0=-1 w 0 a= i=0 n wi xi y= (a)=1/(1+e-a) y (x) is the sigmoid function: 1/(1+e-x) d (x)/dx= (x) (1 - (x)) Derive gradient decent rules to train: • one sigmoid function E/ wi = - p(tp-y) y (1 -y) xip • Multilayer networks of sigmoid units backpropagation:

Gradient Descent Rule for Sigmoid Output Function sigmoid Ep[w 1, …, wn] = ½ (tp-yp)2 Ep/ wi = / wi ½ (tp-yp)2 a ’ a = / wi ½ (tp- ( i wi xip))2 = (tp-yp) ‘( i wi xip) (-xip) for y= (a) = 1/(1+e-a) ’(a)= e-a/(1+e-a)2= (a) (1 - (a)) w’i= wi + wi = wi + y(1 -y)(tp-yp) xip

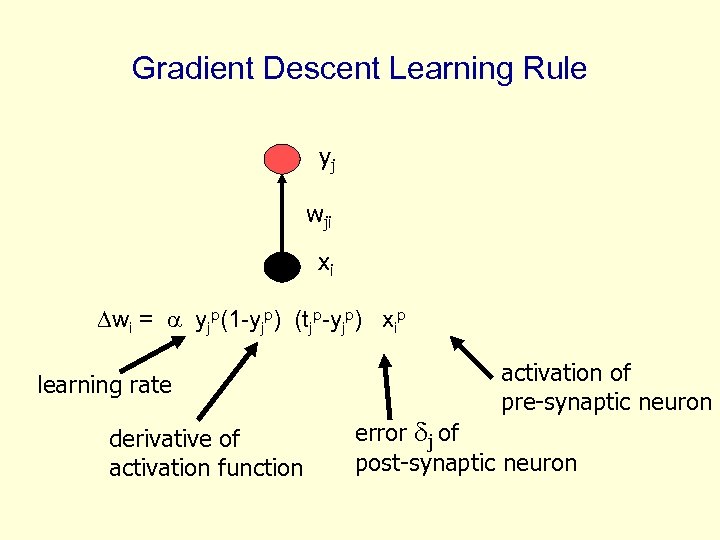Gradient Descent Learning Rule yj wji xi wi = yjp(1 -yjp) (tjp-yjp) xip learning rate derivative of activation function activation of pre-synaptic neuron error j of post-synaptic neuron

Learning with hidden units • Networks without hidden units are very limited in the input-output mappings they can model. – More layers of linear units do not help. Its still linear. – Fixed output non-linearities are not enough • We need multiple layers of adaptive non-linear hidden units. This gives us a universal approximator. But how can we train such nets? – We need an efficient way of adapting all the weights, not just the last layer. This is hard. Learning the weights going into hidden units is equivalent to learning features. – Nobody is telling us directly what hidden units should do.

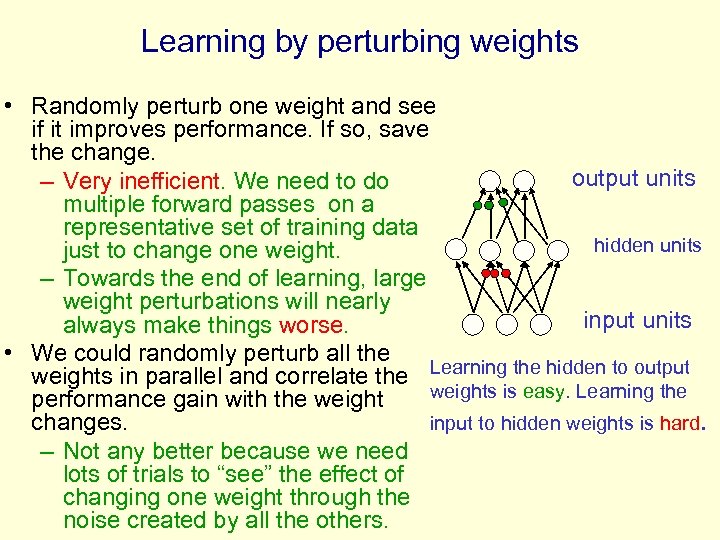Learning by perturbing weights • Randomly perturb one weight and see if it improves performance. If so, save the change. output units – Very inefficient. We need to do multiple forward passes on a representative set of training data hidden units just to change one weight. – Towards the end of learning, large weight perturbations will nearly input units always make things worse. • We could randomly perturb all the weights in parallel and correlate the Learning the hidden to output weights is easy. Learning the performance gain with the weight input to hidden weights is hard. changes. – Not any better because we need lots of trials to “see” the effect of changing one weight through the noise created by all the others.

The idea behind backpropagation • We don’t know what the hidden units ought to do, but we can compute how fast the error changes as we change a hidden activity. – Instead of using desired activities to train the hidden units, use error derivatives w. r. t. hidden activities. – Each hidden activity can affect many output units and can therefore have many separate effects on the error. These effects must be combined. – We can compute error derivatives for all the hidden units efficiently. – Once we have the error derivatives for the hidden activities, its easy to get the error derivatives for the weights going into a hidden unit.

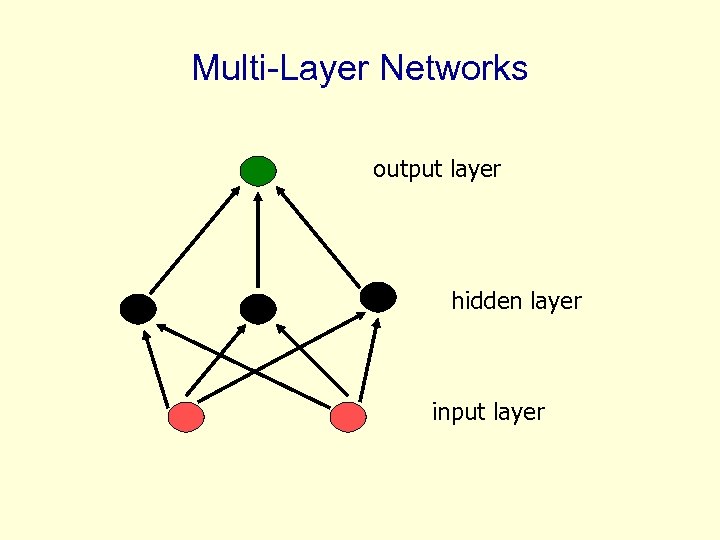Multi-Layer Networks output layer hidden layer input layer

Training-Rule for Weights to the Output Layer yj wji xi Ep[wij] = ½ j (tjp-yjp)2 Ep/ wji = / wji ½ j (tjp-yjp)2 =… = - yjp(1 -ypj)(tpj-ypj) xip wji = yjp(1 -yjp) (tpj-yjp) xip = j p x i p with jp : = yjp(1 -yjp) (tpj-yjp)

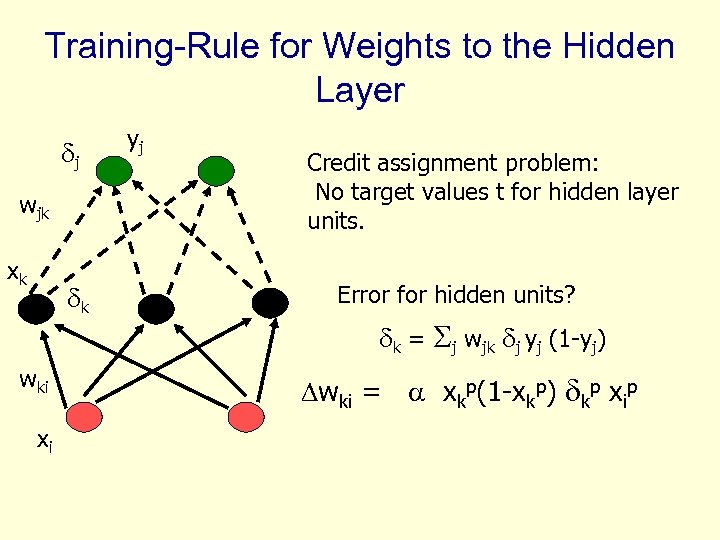Training-Rule for Weights to the Hidden Layer j wjk xk k wki xi yj Credit assignment problem: No target values t for hidden layer units. Error for hidden units? k = j wjk j yj (1 -yj) wki = xkp(1 -xkp) kp xip

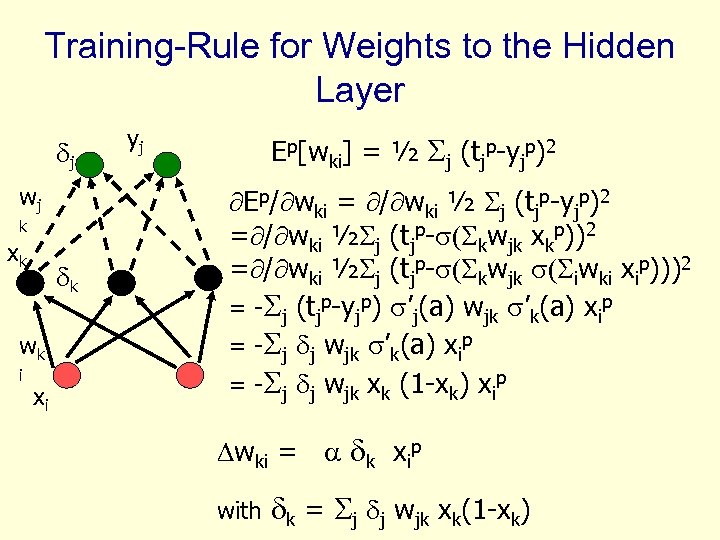Training-Rule for Weights to the Hidden Layer j wj k xk k wk i xi yj Ep[wki] = ½ j (tjp-yjp)2 Ep/ wki = / wki ½ j (tjp-yjp)2 = / wki ½ j (tjp- ( kwjk xkp))2 = / wki ½ j (tjp- ( kwjk ( iwki xip)))2 = - j (tjp-yjp) ’j(a) wjk ’k(a) xip = - j j wjk xk (1 -xk) xip wki = k xip with k = j j wjk xk(1 -xk)

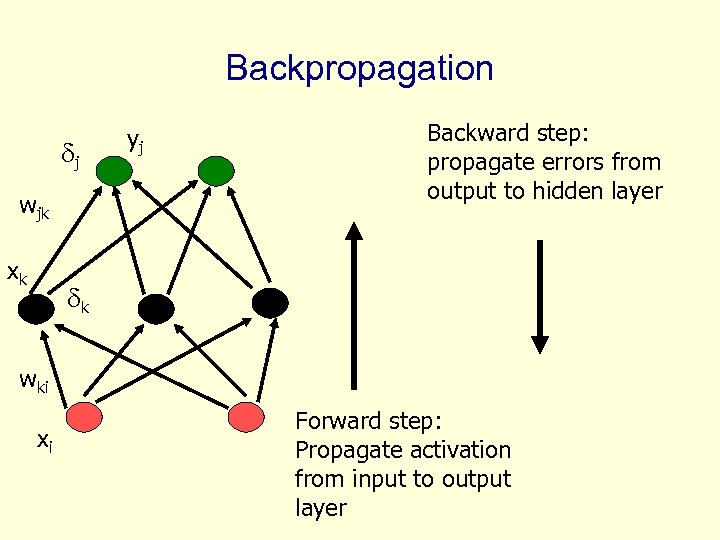Backpropagation j wjk xk yj Backward step: propagate errors from output to hidden layer k wki xi Forward step: Propagate activation from input to output layer

Backpropagation Algorithm • Initialize each wi to some small random value • Until the termination condition is met, Do – For each training example <(x 1, …xn), t> Do • Input the instance (x 1, …, xn) to the network and compute the network outputs yk • For each output unit k – k=yk(1 -yk)(tk-yk) • For each hidden unit h – h=yh(1 -yh) k wh, k k • For each network weight wi, j Do • wi, j=wi, j+ wi, j where wi, j= j xi, j

Backpropagation • Gradient descent over entire network weight vector • Easily generalized to arbitrary directed graphs • Will find a local, not necessarily global error minimum -in practice often works well (can be invoked multiple times with different initial weights) • Often include weight momentum term wi, j(n)= j xi, j + wi, j (n-1) • Minimizes error training examples – Will it generalize well to unseen instances (overfitting)? • Training can be slow typical 1000 -10000 iterations (use Levenberg-Marquardt instead of gradient descent) • Using network after training is fast

Convergence of Backprop Gradient descent to some local minimum perhaps not global minimum • Add momentum term: wki(n) – wki(n) = k(n) xi (n) + l wki(n-1) with l [0, 1] • Stochastic gradient descent • Train multiple nets with different initial weights Nature of convergence • Initialize weights near zero • Therefore, initial networks near-linear • Increasingly non-linear functions possible as training progresses

Optimization Methods • There are other more efficient (faster convergence) optimization methods than gradient descent – Newton’s method uses a quadratic approximation (2 nd order Taylor expansion) – F(x+ x) = F(x) + F(x) x + x 2 F(x) x + … – Conjugate gradients – Levenberg-Marquardt algorithm

NN: Universal Approximator? • Kolmogorov proved that any continuous function g(x) defined on the unit hypercube In can be represented as for properly chosen and . (A. N. Kolmogorov. On the representation of continuous functions of several variables by superposition of continuous functions of one variable and addition. Doklady Akademiia Nauk SSSR, 114(5): 953 -956, 1957)

Universal Approximation Property of ANN Boolean functions • Every boolean function can be represented by network with single hidden layer • But might require exponential (in number of inputs) hidden units Continuous functions • Every bounded continuous function can be approximated with arbitrarily small error, by network with one hidden layer [Cybenko 1989, Hornik 1989] • Any function can be approximated to arbitrary accuracy by a network with two hidden layers [Cybenko 1988]

Ways to use weight derivatives • How often to update – after each training case? – after a full sweep through the training data? • How much to update – Use a fixed learning rate? – Adapt the learning rate? – Add momentum? – Don’t use steepest descent?

Applications of neural networks • Alvinn (the neural network that learns to drive a van from camera inputs). • NETtalk: a network that learns to pronounce English text. • Recognizing hand-written zip codes. • Lots of applications in financial time series analysis.

NETtalk (Sejnowski & Rosenberg, 1987) • The task is to learn to pronounce English text from examples. • Training data is 1024 words from a side-by-side English/phoneme source. • Input: 7 consecutive characters from written text presented in a moving window that scans text. • Output: phoneme code giving the pronunciation of the letter at the center of the input window. • Network topology: 7 x 29 inputs (26 chars + punctuation marks), 80 hidden units and 26 output units (phoneme code). Sigmoid units in hidden and output layer.

NETtalk (contd. ) • Training protocol: 95% accuracy on training set after 50 epochs of training by full gradient descent. 78% accuracy on a set-aside test set. • Comparison against Dectalk (a rule based expert system): Dectalk performs better; it represents a decade of analysis by linguists. NETtalk learns from examples alone and was constructed with little knowledge of the task.

Overfitting • The training data contains information about the regularities in the mapping from input to output. But it also contains noise – The target values may be unreliable. – There is sampling error. There will be accidental regularities just because of the particular training cases that were chosen. • When we fit the model, it cannot tell which regularities are real and which are caused by sampling error. – So it fits both kinds of regularity. – If the model is very flexible it can model the sampling error really well. This is a disaster.

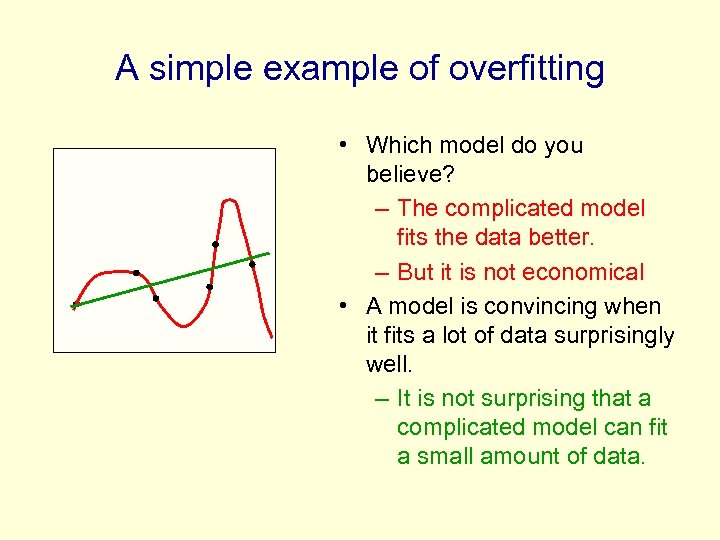A simple example of overfitting • Which model do you believe? – The complicated model fits the data better. – But it is not economical • A model is convincing when it fits a lot of data surprisingly well. – It is not surprising that a complicated model can fit a small amount of data.

Generalization • The objective of learning is to achieve good generalization to new cases, otherwise just use a look-up table. • Generalization can be defined as a mathematical interpolation or regression over a set of training points: f(x) x

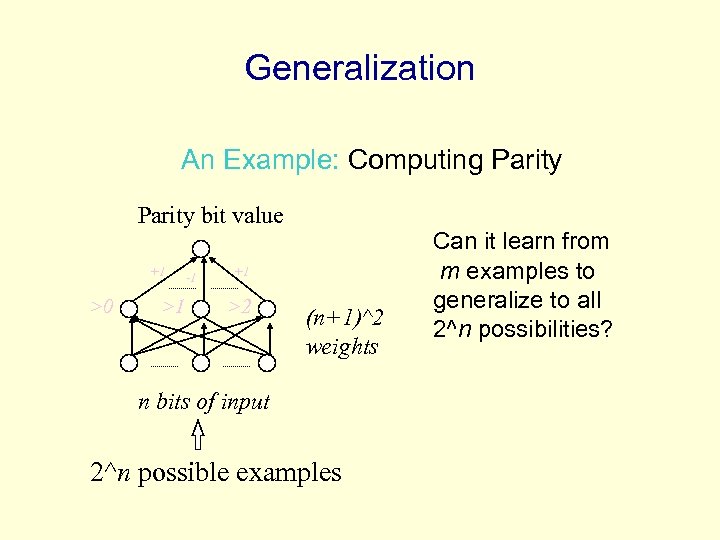Generalization An Example: Computing Parity bit value +1 >0 >1 -1 +1 >2 (n+1)^2 weights n bits of input 2^n possible examples Can it learn from m examples to generalize to all 2^n possibilities?

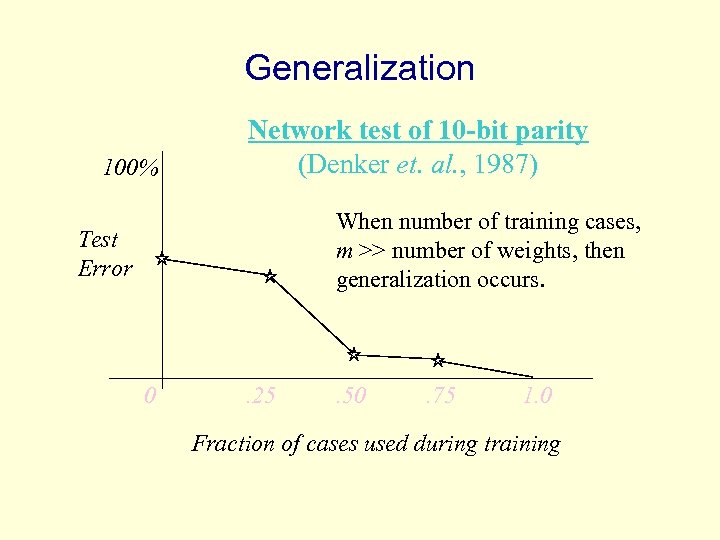Generalization 100% Network test of 10 -bit parity (Denker et. al. , 1987) When number of training cases, m >> number of weights, then generalization occurs. Test Error 0 . 25 . 50 . 75 1. 0 Fraction of cases used during training

Generalization A Probabilistic Guarantee N = # hidden nodes m = # training cases W = # weights = error tolerance (< 1/8) Network will generalize with 95% confidence if: 1. Error on training set < 2. Based on PAC theory => provides a good rule of practice.

Generalization • The objective of learning is to achieve good generalization to new cases, otherwise just use a look-up table. • Generalization can be defined as a mathematical interpolation or regression over a set of training points: f(x) x

Generalization Over-Training • Is the equivalent of over-fitting a set of data points to a curve which is too complex • Occam’s Razor (1300 s) : “plurality should not be assumed without necessity” • The simplest model which explains the majority of the data is usually the best

Generalization Preventing Over-training: • Use a separate test or tuning set of examples • Monitor error on the test set as network trains • Stop network training just prior to over-fit error occurring - early stopping or tuning • Number of effective weights is reduced • Most new systems have automated early stopping methods

Generalization Weight Decay: an automated method of effective weight control • Adjust the bp error function to penalize the growth of unnecessary weights: where: = weight -cost parameter is decayed by an amount proportional to its magnitude; those not reinforced => 0

Network Design & Training Issues Design: • Architecture of network • Structure of artificial neurons • Learning rules Training: • • Ensuring optimum training Learning parameters Data preparation and more. .

Network Design Architecture of the network: How many nodes? • Determines number of network weights • How many layers? • How many nodes per layer? Input Layer Hidden Layer Output Layer • Automated methods: – augmentation (cascade correlation) – weight pruning and elimination

Network Design Architecture of the network: Connectivity? • Concept of model or hypothesis space • Constraining the number of hypotheses: – selective connectivity – shared weights – recursive connections

Network Design Structure of artificial neuron nodes • Choice of input integration: – summed, squared and summed – multiplied • Choice of activation (transfer) function: – sigmoid (logistic) – hyperbolic tangent – Guassian – linear – soft-max

Network Design Selecting a Learning Rule • • Generalized delta rule (steepest descent) Momentum descent Advanced weight space search techniques Global Error function can also vary - normal - quadratic - cubic

Network Training How do you ensure that a network has been well trained? • Objective: To achieve good generalization accuracy on new examples/cases • Establish a maximum acceptable error rate • Train the network using a validation test set to tune it • Validate the trained network against a separate test set which is usually referred to as a production test set

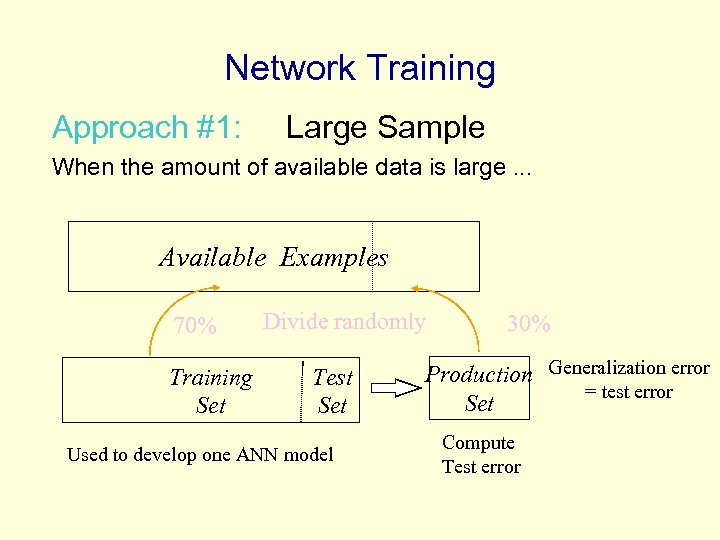Network Training Approach #1: Large Sample When the amount of available data is large. . . Available Examples 70% Training Set Divide randomly Test Set Used to develop one ANN model 30% Production Generalization error = test error Set Compute Test error

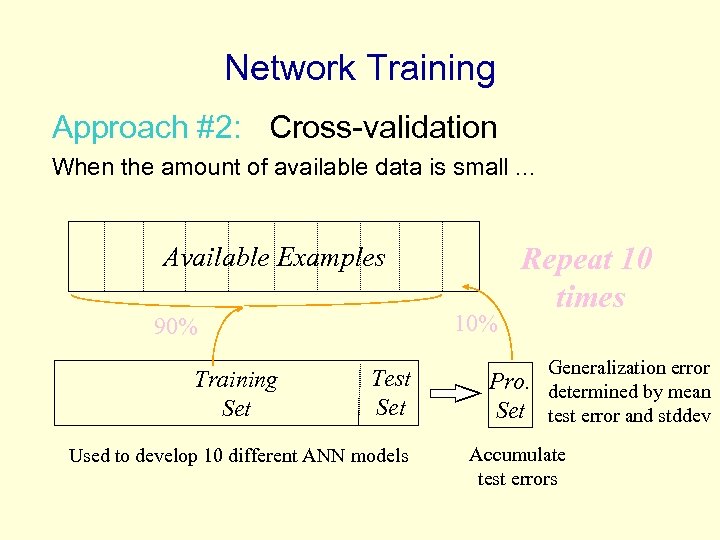Network Training Approach #2: Cross-validation When the amount of available data is small. . . Available Examples 10% 90% Training Set Test Set Used to develop 10 different ANN models Repeat 10 times Pro. Set Generalization error determined by mean test error and stddev Accumulate test errors

Network Training How do you select between two ANN designs ? • A statistical test of hypothesis is required to ensure that a significant difference exists between the error rates of two ANN models • If Large Sample method has been used then apply Mc. Nemar’s test* • If Cross-validation then use a paired t test for difference of two proportions *We assume a classification problem, if this is function approximation then use paired t test for difference of means

Network Training Mastering ANN Parameters Typical learning rate momentum weight-cost - Range 0. 1 0. 01 - 0. 99 0. 8 0. 1 - 0. 9 0. 1 0. 001 - 0. 5 Fine tuning : - adjust individual parameters at each node and/or connection weight – automatic adjustment during training

Network Training Network weight initialization • Random initial values +/- some range • Smaller weight values for nodes with many incoming connections • Rule of thumb: initial weight range should be approximately coming into a node

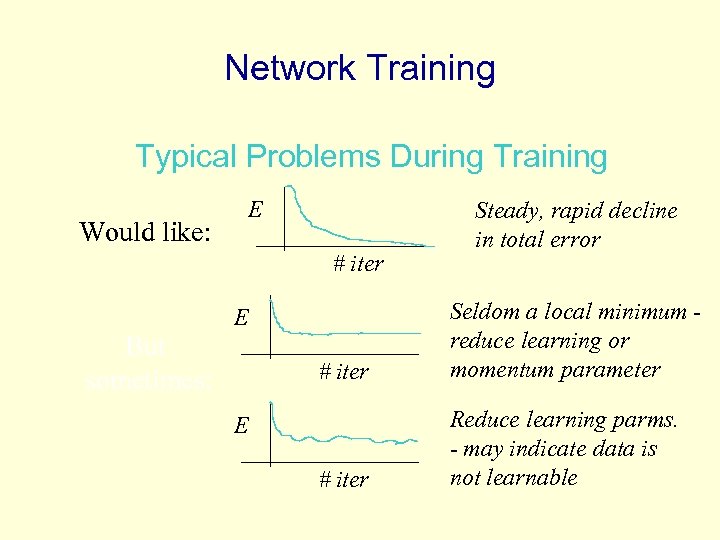Network Training Typical Problems During Training E Would like: # iter Steady, rapid decline in total error # iter Seldom a local minimum reduce learning or momentum parameter # iter Reduce learning parms. - may indicate data is not learnable E But sometimes: E

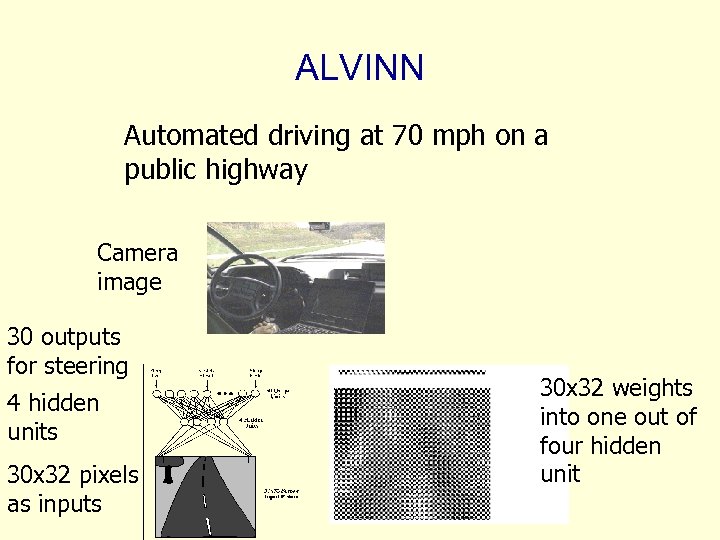ALVINN Automated driving at 70 mph on a public highway Camera image 30 outputs for steering 4 hidden units 30 x 32 pixels as inputs 30 x 32 weights into one out of four hidden unit

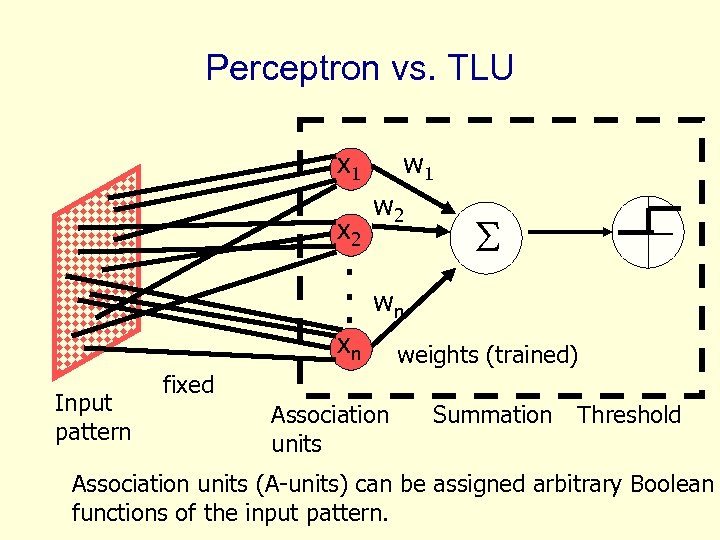Perceptron vs. TLU w 1 x 2 . . . w 2 wn xn Input pattern weights (trained) fixed Association units Summation Threshold Association units (A-units) can be assigned arbitrary Boolean functions of the input pattern.

Gradient Descent Learning Rule • Consider linear unit without threshold and continuous output o (not just – 1, 1) – o=w 0 + w 1 x 1 + … + wn xn • Train the wi’s such that they minimize the squared error – E[w 1, …, wn] = ½ d D (td-od)2 where D is the set of training examples

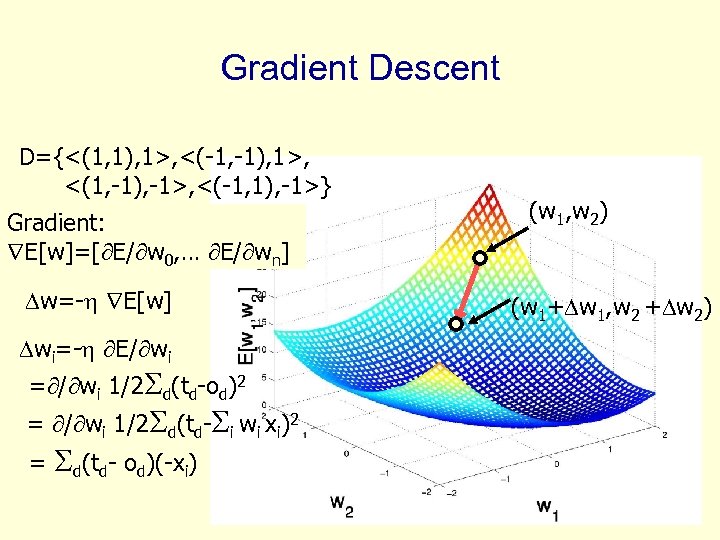Gradient Descent D={<(1, 1), 1>, <(-1, -1), 1>, <(1, -1), -1>, <(-1, 1), -1>} Gradient: E[w]=[ E/ w 0, … E/ wn] w=- E[w] wi=- E/ wi = / wi 1/2 d(td-od)2 = / wi 1/2 d(td- i wi xi)2 = d(td- od)(-xi) (w 1, w 2) (w 1+ w 1, w 2 + w 2)

Gradient Descent Gradient-Descent(training_examples, ) Each training example is a pair of the form <(x 1, …xn), t> where (x 1, …, xn) is the vector of input values, and t is the target output value, is the learning rate (e. g. 0. 1) • Initialize each wi to some small random value • Until the termination condition is met, Do – Initialize each wi to zero – For each <(x 1, …xn), t> in training_examples Do • Input the instance (x 1, …, xn) to the linear unit and compute the output o • For each linear unit weight wi Do – wi= wi + (t-o) xi – For each linear unit weight wi Do • wi=wi+ wi

Literature • Neural Networks – A Comprehensive Foundation, Simon Haykin, Prentice-Hall, 1999 • Networks for Pattern Recognition”, C. M. Bishop, Oxford University Press, 1996 • ”Neural Network Design”, M. Hagan et al, PWS, 1995 • Perceptrons: An Introduction to Computational Geometry, Minsky, Papert, 1969

Software • Neural Networks for Face Recognition http: //www. cs. cmu. edu/afs/cs. cmu. edu/user/mitchell/ftp/faces. html • SNNS Stuttgart Neural Networks Simulator http: //www-ra. informatik. uni-tuebingen. de/SNNS • Neural Networks at your fingertips http: //www. geocities. com/Cape. Canaveral/1624/ • Neural Network Design Demonstrations http: //ee. okstate. edu/mhagan/nndesign_5. ZIP • Bishop’s network toolbox • Matlab Neural Network toolbox

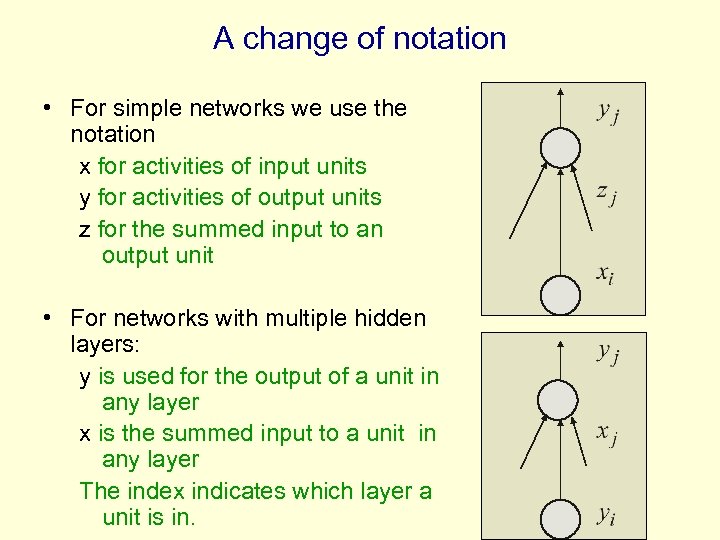A change of notation • For simple networks we use the notation x for activities of input units y for activities of output units z for the summed input to an output unit • For networks with multiple hidden layers: y is used for the output of a unit in any layer x is the summed input to a unit in any layer The index indicates which layer a unit is in.

Non-linear neurons with smooth derivatives • For backpropagation, we need neurons that have well-behaved derivatives. – Typically they use the logistic function – The output is a smooth function of the inputs and the weights. 1 0. 5 0 0 Its odd to express it in terms of y.

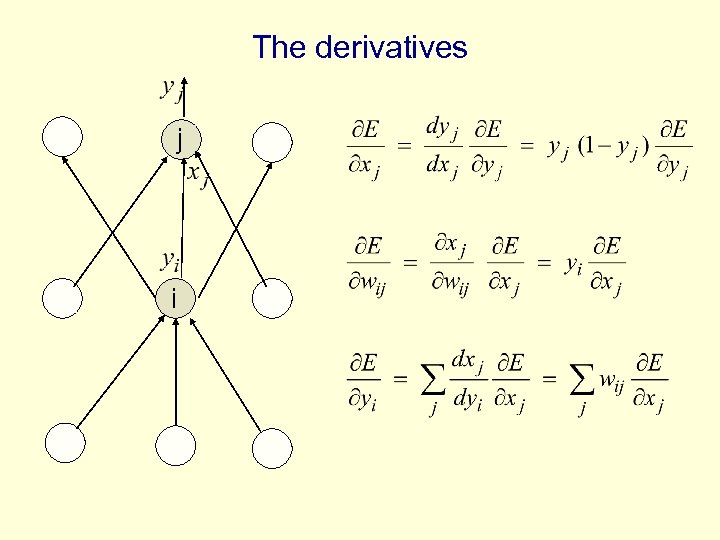
Sketch of the backpropagation algorithm on a single training case • First convert the discrepancy between each output and its target value into an error derivative. • Then compute error derivatives in each hidden layer from error derivatives in the layer above. • Then use error derivatives w. r. t. activities to get error derivatives w. r. t. the weights.

The derivatives j i

Momentum • Sometimes we add to ΔWji a momentum factor α. This allows us to use a high learning rate, but prevent the oscillatory behavior that can sometimes result from a high learning rate. Add to this a momentum α times the weight update from the last iteration, i. e. , add α times the previous value of where and often α = 0. 9 Momentum keeps it going in the same direction.

More on backpropagation • Performs gradient descent over the entire network weight vector. • Will find a local, not necessarily global, error minimum. • Minimizes error over training set; need to guard against overfitting just as with decision tree learning. • Training takes thousands of iterations (epochs) --- slow!

Network topology • Designing network topology is an art. • We can learn the network topology using genetic algorithms. But using GAs is very cpu-intensive. An alternative that people use is hill-climbing.

First MLP Exercise (Due June 19) • Become familiar with the Neural Network Toolbox in Matlab • Construct a single hidden layer, feed forward network with sigmoidal units. to output. The network should have n hidden units n=3 to 6. • Construct two more networks of same nature with n-1 and n+1 hidden units respectively. • Initial random weights are from ~ N(µ, σ2) • The dimensionality of the input data is d

First MLP Exercise (Cntd) • Constructing the a train and test set of size M • For simplicity, choose two distributions N(-1, σ2) and N(1, σ2). Choose M/2 samples of d dimensions from the first distribution and M/2 from the second. This way you get a set of M vectors in d dimensions. Give the first set a class label of 0 and the second set a class label of 1. • Repeat this again for the construction of the test set.

Actual Training • Train 5 networks with the same training data (each network has different initial conditions) • Construct a classification error graph for both train and test data taken at different time steps (mean and std over 5 nets) • Repeat for n=3 -6 using both n+1 and n-1 • Discuss the results, justify with graphs and provide clear understanding • (you may try other setups to test your understanding) • Consider momentum and weight deca

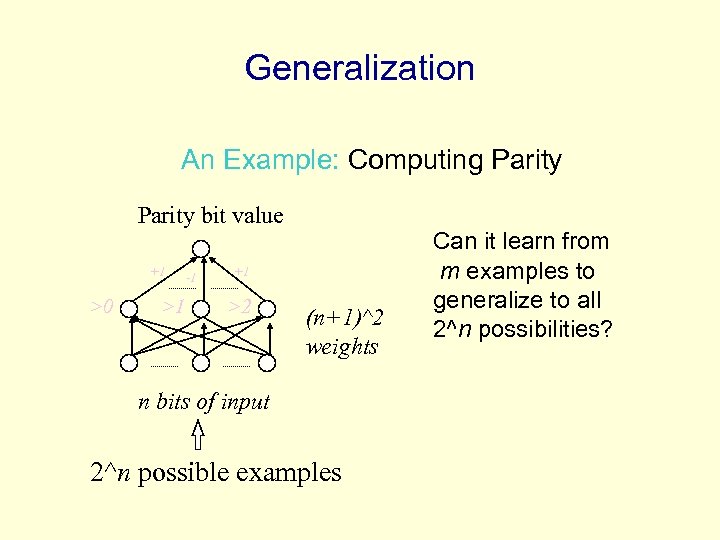Generalization An Example: Computing Parity bit value +1 >0 >1 -1 +1 >2 (n+1)^2 weights n bits of input 2^n possible examples Can it learn from m examples to generalize to all 2^n possibilities?

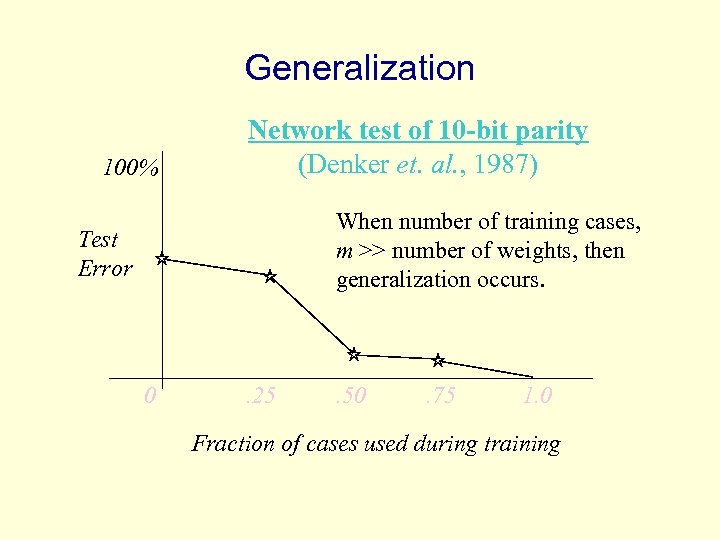Generalization 100% Network test of 10 -bit parity (Denker et. al. , 1987) When number of training cases, m >> number of weights, then generalization occurs. Test Error 0 . 25 . 50 . 75 1. 0 Fraction of cases used during training

Generalization Consider 20 -bit parity problem: • 20 -20 -1 net has 441 weights • For 95% confidence that net will predict with , we need training examples • Not bad considering

Generalization Training Sample & Network Complexity Based on : W - to reduced size of training sample W - to supply freedom Optimum W=> Optimum # Hidden Nodes to construct desired function

Generalization How can we control number of effective weights? • Manually or automatically select optimum number of hidden nodes and connections • Prevent over-fitting = over-training • Add a weight-cost term to the bp error equation

Generalization Consider 20 -bit parity problem: • 20 -20 -1 net has 441 weights • For 95% confidence that net will predict with , we need training examples • Not bad considering