МОУ лицей 1 г Иркутска Подготовка к

МОУ лицей № 1 г. Иркутска Подготовка к ЕГЭ Мельникова М. И. 1

МОУ лицей № 1 г. Иркутска • Повторить основные группы задач, связанных с целыми числами 2

МОУ лицей № 1 г. Иркутска • Усвоение методов и стиля, свойственных математике • Обеспечение уровневого подхода к организации повторения • Подготовка к ЕГЭ 3

Нейман, 2011, С 6, Вариант 1 Для изготовления изделий двух видов имеется 100 кг металла. На изготовление изделия 1 -го вида расходуется 2 кг металла, а изделия 2 -го вида – 4 кг. Какую наибольшую прибыль (в рублях) может получить предприятие от продажи изделий, если отпускная способность изделия 1 -го вида составляет 300 руб. , а 2 -го – 200 руб. , причем изделий первого вида нужно изготовить не более 40, а 2 -го – не более 200?

Предлагаемое авторское решение 5

Другое решение Математическая модель: х – у – единиц продукции 1 -го вида изготовит предприятие единиц продукции 2 -го вида изготовит предприятие По условию: х ≤ 40 у ≤ 20 Понадобится металла: 2 х + 4 у (кг) 2 х + 4 у 100 Прибыль предприятия: P(x; y) = 300 x + 200 y

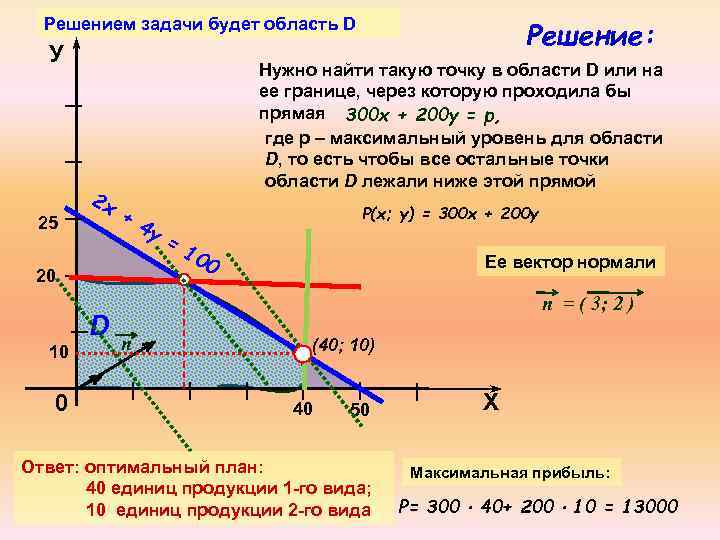Решением задачи будет область D У 25 2 х Нужно найти такую точку в области D или на ее границе, через которую проходила бы прямая 300 x + 200 y = р, где р – максимальный уровень для области D, то есть чтобы все остальные точки области D лежали ниже этой прямой + 20 D 10 0 Решение: 4 у P(x; y) = 300 x + 200 y = 10 0 Ее вектор нормали n = ( 3; 2 ) n (40; 10) 40 50 Ответ: оптимальный план: 40 единиц продукции 1 -го вида; 10 единиц продукции 2 -го вида Х Максимальная прибыль: P= 300 40+ 200 10 = 13000

Можно воспользоваться тем, что свои наибольшее и наименьшее значения линейная функция достигает в вершинах многоугольника ограничений Это свойство является основным в задачах оптимизации

Для изготовления изделия А нужно затратить 20 часов работы токарного станка и 30 ч работы фрезерного станка. Для изготовления изделия В нужно затратить 10 часов работы токарного станка и 40 ч работы фрезерного станка. Ресурсы времени работы токарных станков равны 2000 станкочасов. Ресурсы времени работы фрезерных станков равны 4800 станкочасов. Прибыль от реализации 1 единицы изделия А или изделия В составляет 400 денежных единиц. Составить оптимальный план выпуска изделий А и В из условия максимума прибыли.

Математическая модель: х – количество изделий А у – количество изделий В По условию: х 0 у 0 Работа токарных станков: 20 х + 10 у (ч) 20 х + 10 у 2000 Работа фрезерных станков: 30 х + 40 у (ч) 30 х + 40 у 4800 Прибыль цеха: P(x; y) = 400 x + 400 y

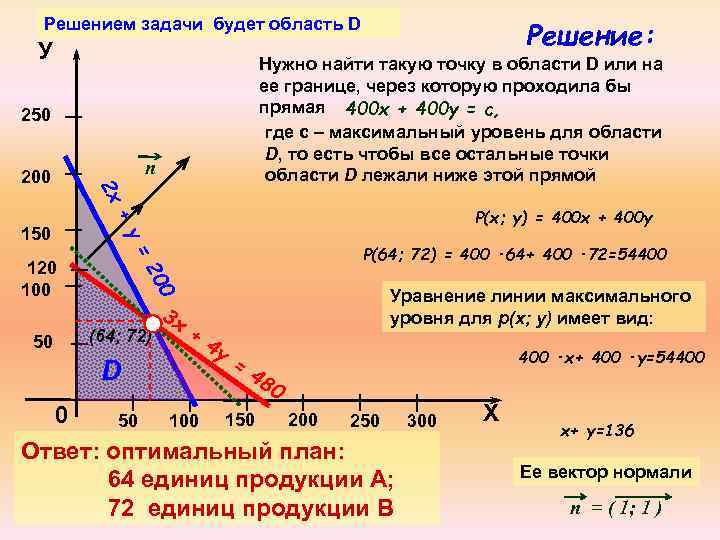Решением задачи будет область D У Нужно найти такую точку в области D или на ее границе, через которую проходила бы прямая 400 x + 400 y = c, где с – максимальный уровень для области D, то есть чтобы все остальные точки области D лежали ниже этой прямой 250 n 2 х 200 Решение: + P(x; y) = 400 x + 400 y Уравнение линии максимального уровня для р(х; у) имеет вид: 0 50 Р(64; 72) = 400 ∙ 64+ 400 ∙ 72=54400 20 100 у= 150 (64; 72) D 3 х + 4 у = 400 ∙х+ 400 ∙у=54400 48 0 0 200 50 100 150 250 Ответ: оптимальный план: 64 единиц продукции А; 72 единиц продукции В 300 Х х+ у=136 Ее вектор нормали n = ( 1; 1 )

Секреты успешного решения конкурсных задач Каждый ученик умеет решать задачи, необходимо только систематизировать знания учащегося. Необходимо выработать систему подготовки учащихся к экзаменам. Наши ученики умные, талантливые ребята, нестандартно мыслящие, им нужна педагогическая помощь, я хочу дать толчок учащимся на дальнейшее развитие. Я не верю, что человек может быть не способен к математике. Чтобы заинтересовать ученика, надо самому любить свой предмет. И верить в учеников своих. Каждый ребенок талантлив. Он таким родился. Надо просто помочь ребенку раскрыть его. И не нужно бояться, что он не справится… 12