МОУ «Гимназия № 12» Преобразование подобия Выполнила: ученица 11 б класса Филиппова Анна 2011
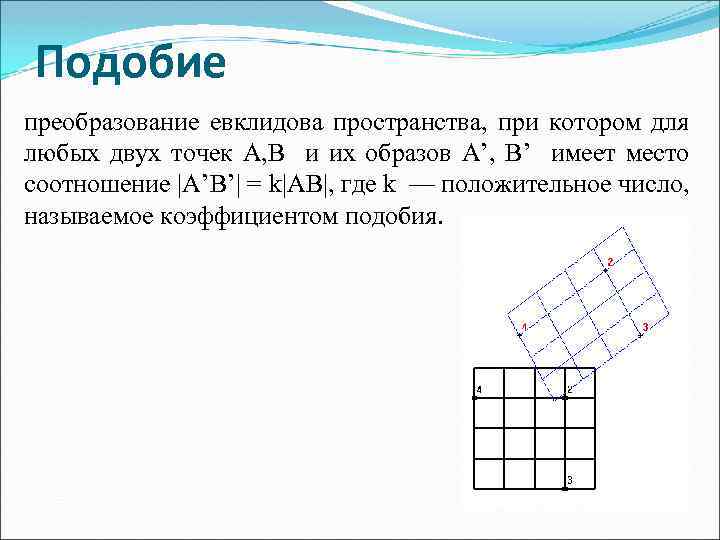
Подобие преобразование евклидова пространства, при котором для любых двух точек А, В и их образов А’, B’ имеет место соотношение |A’B’| = k|AB|, где k — положительное число, называемое коэффициентом подобия.
Примеры Каждая гомотетия является подобием. Каждое движение (в том числе и тождественное) также можно рассматривать как преобразование подобия с коэффициентом k=1. Если преобразовании фигуры F в фигуру F` расстояние между точками изменяется в одно и тоже число раз, то такое преобразование называется преобразованием подобия. Т. е. произвольные точки AB фигуры F переходят в точки A`B` фигуры F`, так что A`B` =k*AB. Число k – это коэффициент подобия.
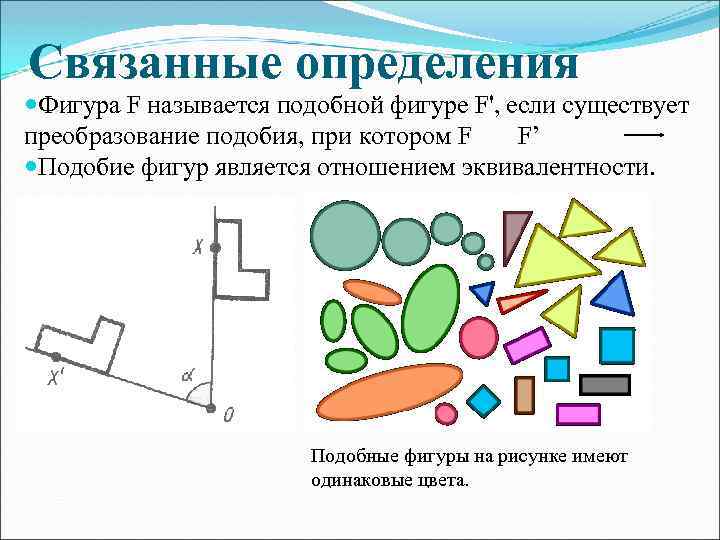
Связанные определения Фигура F называется подобной фигуре F', если существует преобразование подобия, при котором F F’ Подобие фигур является отношением эквивалентности. Подобные фигуры на рисунке имеют одинаковые цвета.
Свойства Подобие есть взаимно однозначное отображение евклидова пространства на себя. Подобие сохраняет порядок точек на прямой, то есть если точка B лежит между точками A, C и B’, A’, C’ — соответствующие их образы при некотором подобии, то B’ также лежит между точками A’ и C’. Точки, не лежащие на прямой, при любом подобии переходят в точки, не лежащие на одной прямой. Подобие преобразует прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность. При подобии угол сохраняет величину. Подобие с коэффициентом k≠ 1, преобразующее каждую прямую в параллельную ей прямую, является гомотетией с коэффициентом k или -k.
Каждое подобие можно рассматривать как композицию движения D и некоторой гомотетии Γ с положительным коэффициентом. Подобие называется собственным (несобственным), если движение D является собственным (несобственным). Собственное подобие сохраняет ориентацию фигур, а несобственное — изменяет ориентацию на противоположную. Два треугольника являются подобными, если: Ø их соответственные углы равны, или Ø стороны пропорциональны. См. также Признаки подобия треугольников. Площади подобных фигур пропорциональны квадратам их сходственных линий (например, сторон). Так, площади кругов пропорциональны отношению квадратов их диаметров (или радиусов).
Обобщения Аналогично определяется подобие (с сохранением указанных выше свойств) в 3 -мерном евклидовом пространстве, а также в nмерном евклидовом и псевдоевклидовом пространствах. В метрических пространствах так же, как в n-мерных римановых, псевдоримановых и финслеровых пространствах подобие определяется как преобразование, переводящее метрику пространства в себя с точностью до постоянного множителя. Совокупность всех подобий n-мерного евклидова, псевдоевклидова, риманова, псевдориманова или финслерова пространства составляет r-членную группу преобразований Ли, называемой группой подобных (гомотетических) преобразований соответствующего пространства. В каждом из пространств указанных типов r -членная группа подобных преобразований Ли содержит (r-1) -членную нормальную подгруппу движений.
Спасибо за внимание!
Гомотетия (от др. -греч. ὁμός — «одинаковый» и θετος — «расположенный» ) — один из видов преобразований подобия. Гомотетией c центром O и коэффициентом k (k≠ 0) называют преобразование плоскости (или пространства), переводящее точку X в точку X', обладающую тем свойством, что. Гомотетию с центром O и коэффициентом k часто обозначают через.
Изометрия (математика) Изометрия, или движение, или (реже) наложение — биекция (преобразование), которая сохраняет расстояние между соответствующими точками, то есть если A' и B' — образы точек A и B, то | A'B' | = | AB |. Термин «изометрия» более распространён в метрической геометрии, в частности, в римановой геометрии. В общем случае метрического пространства (например, для неплоского риманова многообразия) движения могут существовать далеко не всегда. Термин «движение» более распространён в евклидовой геометрии и смежных областях.
Скачать презентацию МОУ Гимназия 12 Преобразование подобия Выполнила ученица
Преобразование подобия)1.ppt