Motor cortex Somatosensory cortex Sensory associative cortex Pars

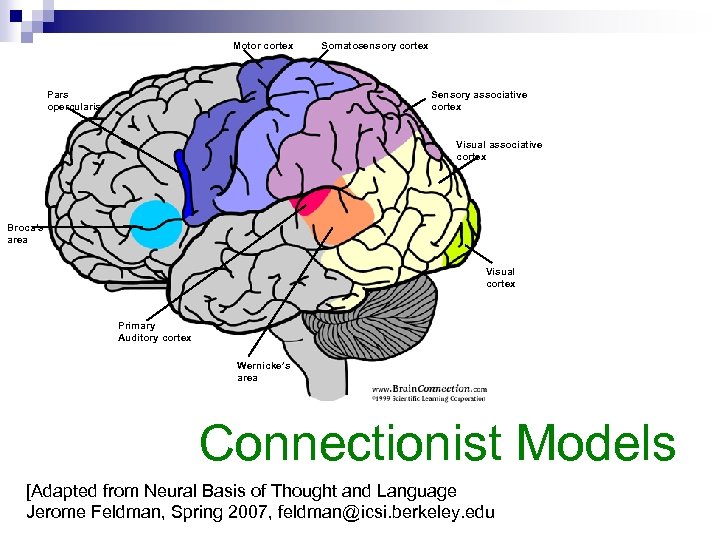Motor cortex Somatosensory cortex Sensory associative cortex Pars opercularis Visual associative cortex Broca’s area Visual cortex Primary Auditory cortex Wernicke’s area Connectionist Models [Adapted from Neural Basis of Thought and Language Jerome Feldman, Spring 2007, feldman@icsi. berkeley. edu

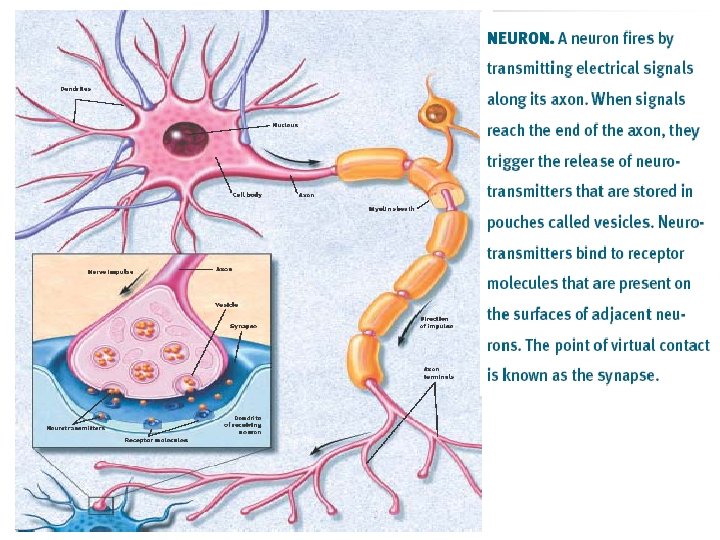
Neural networks abstract from the details of real neurons n n Conductivity delays are neglected An output signal is either discrete (e. g. , 0 or 1) or it is a real-valued number (e. g. , between 0 and 1) Net input is calculated as the weighted sum of the input signals Net input is transformed into an output signal via a simple function (e. g. , a threshold function)

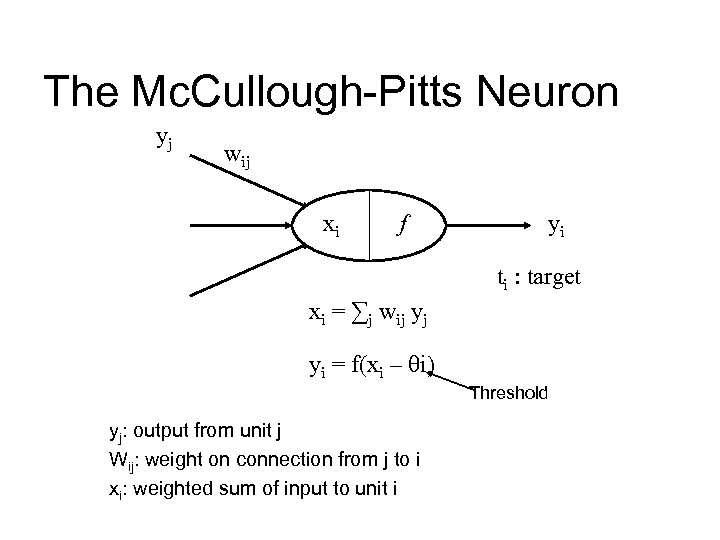The Mc. Cullough-Pitts Neuron yj wij xi f yi ti : target xi = ∑j wij yj yi = f(xi – qi) Threshold yj: output from unit j Wij: weight on connection from j to i xi: weighted sum of input to unit i

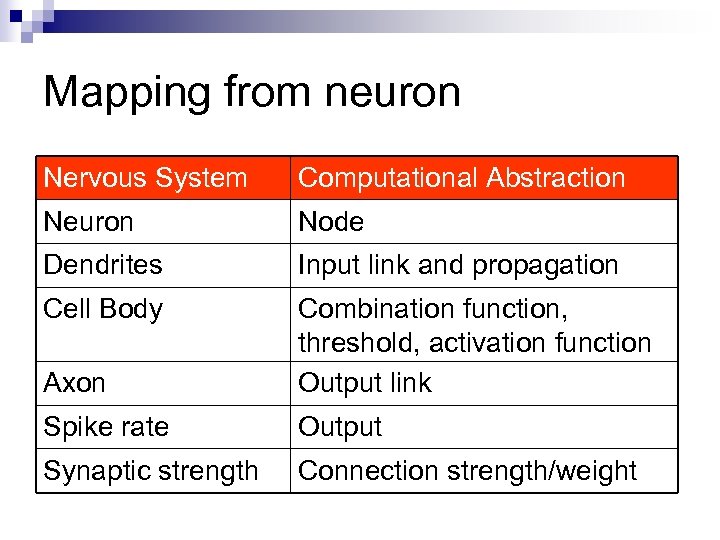Mapping from neuron Nervous System Computational Abstraction Neuron Node Dendrites Input link and propagation Cell Body Axon Combination function, threshold, activation function Output link Spike rate Output Synaptic strength Connection strength/weight

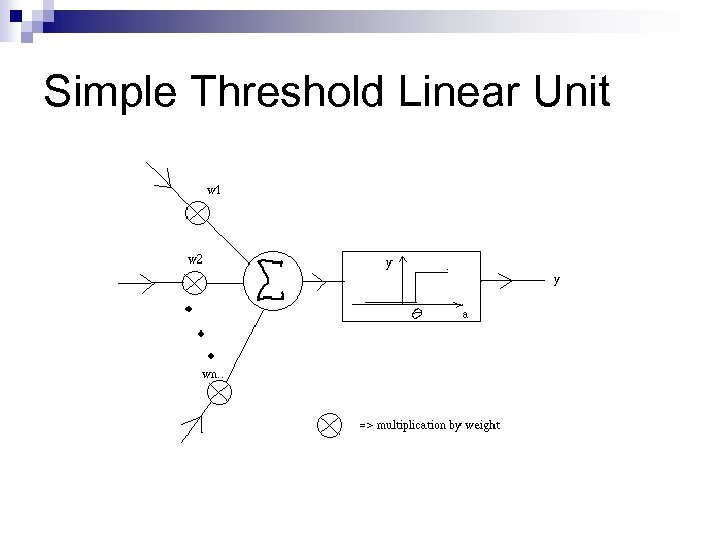Simple Threshold Linear Unit

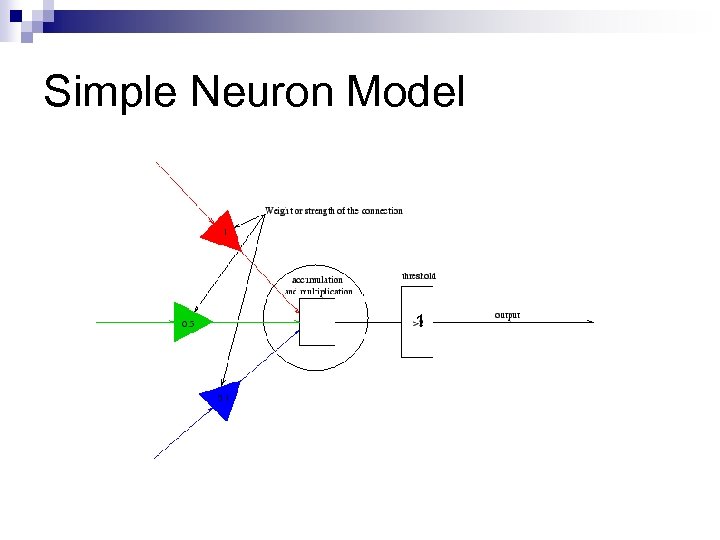Simple Neuron Model 1

A Simple Example a = x 1 w 1+x 2 w 2+x 3 w 3. . . +xnwn. a= 1*x 1 + 0. 5*x 2 +0. 1*x 3 x 1 =0, x 2 = 1, x 3 =0 Net(input) = f = 0. 5 Threshold bias = 1 Net(input) – threshold bias< 0 Output = 0

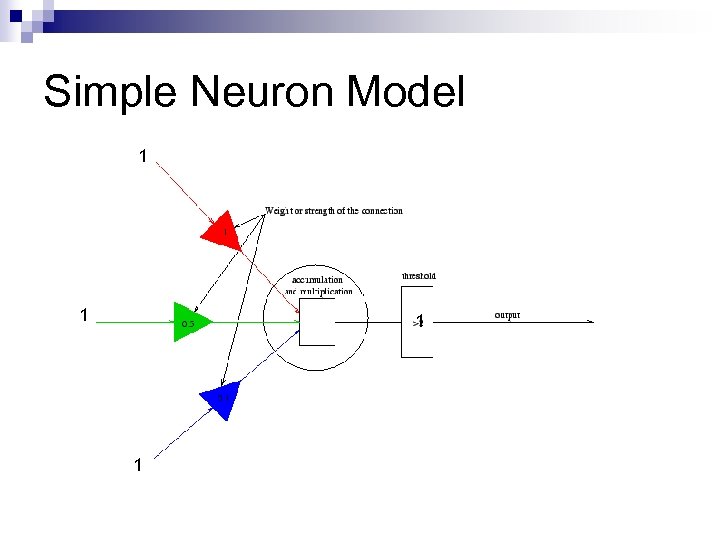Simple Neuron Model 1 1

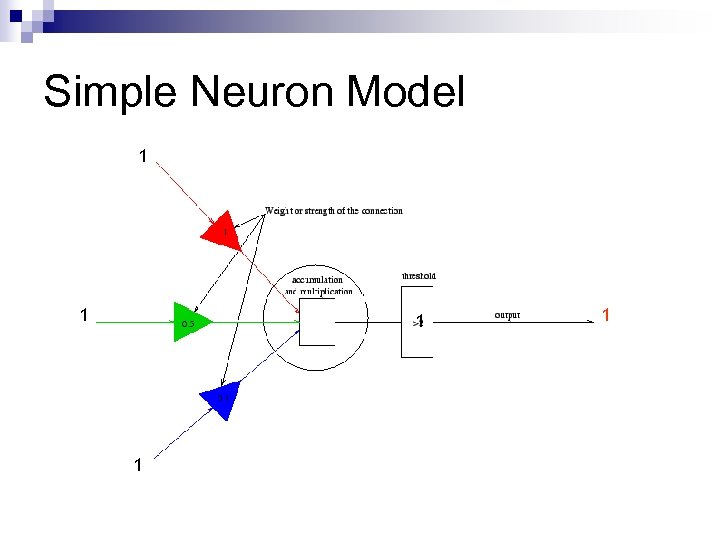Simple Neuron Model 1 1 1

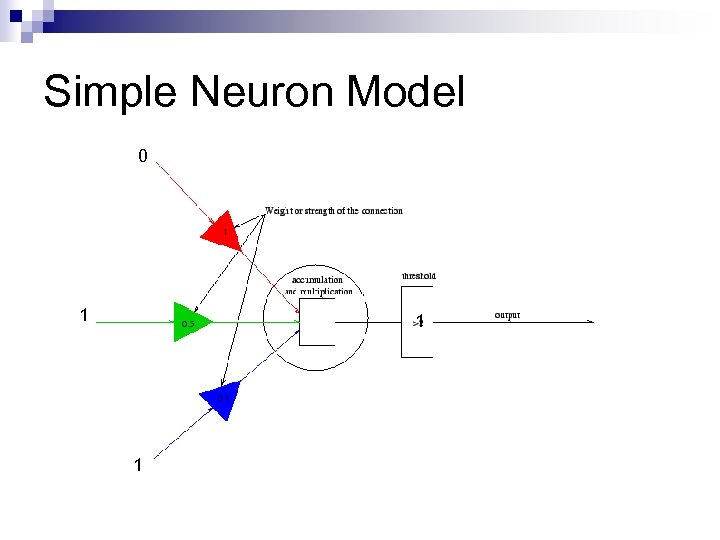Simple Neuron Model 0 1 1 1

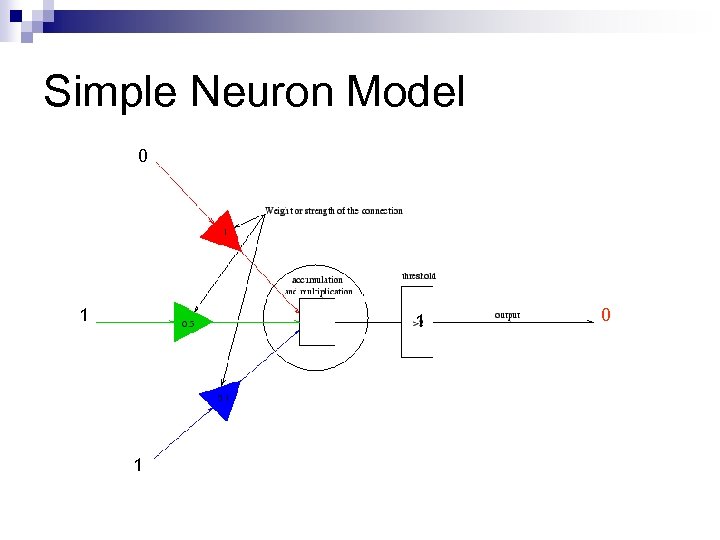Simple Neuron Model 0 1 1 1 0

Different Activation Functions BIAS UNIT With X 0 = 1 Threshold Activation Function (step) n Piecewise Linear Activation Function n Sigmoid Activation Funtion n Gaussian Activation Function n ¨ Radial Basis Function

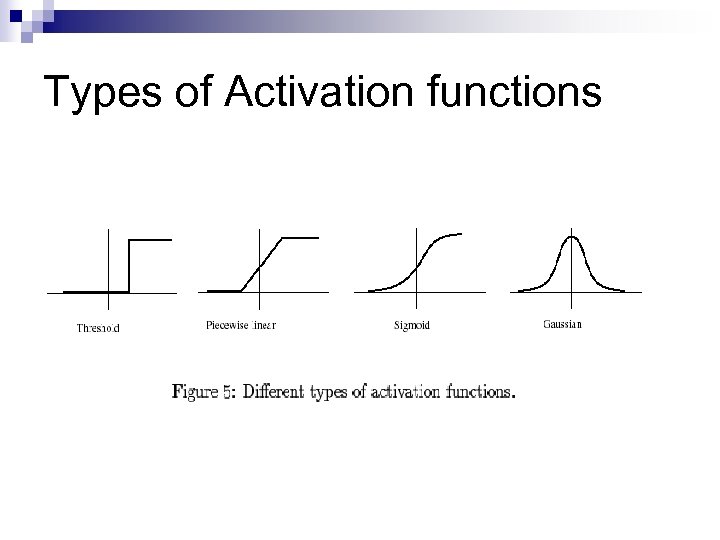Types of Activation functions

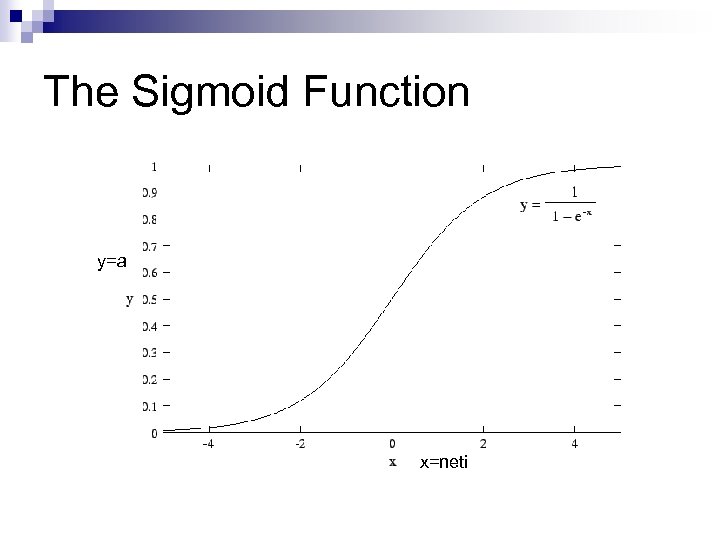The Sigmoid Function y=a x=neti

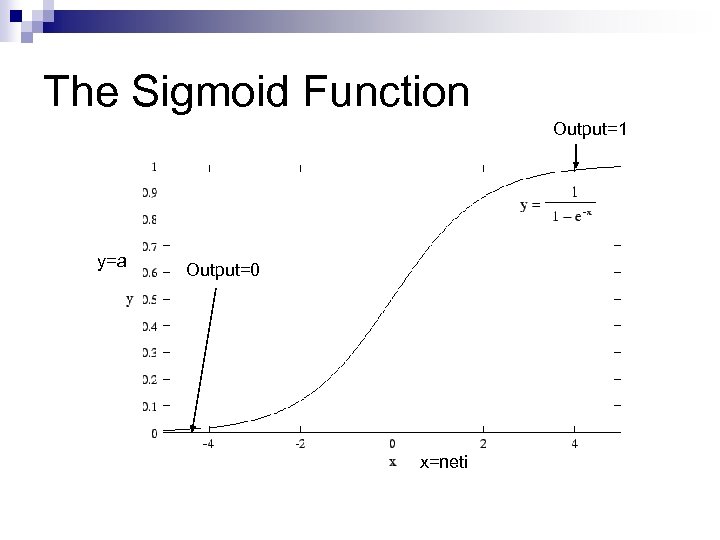The Sigmoid Function Output=1 y=a Output=0 x=neti

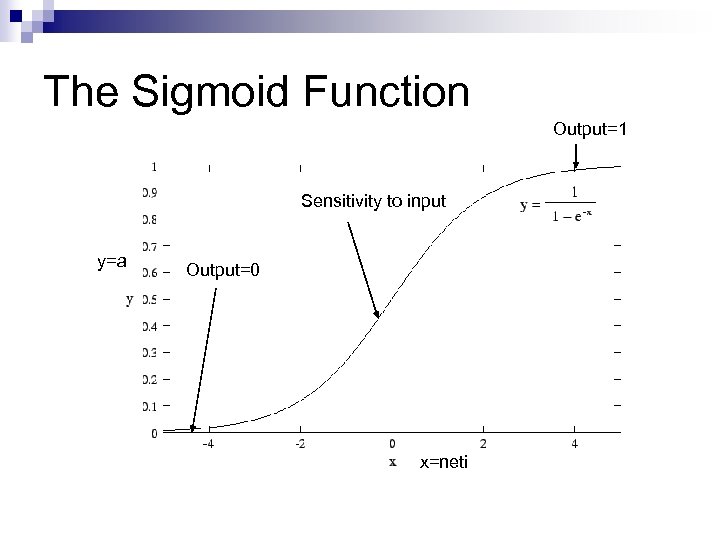The Sigmoid Function Output=1 Sensitivity to input y=a Output=0 x=neti

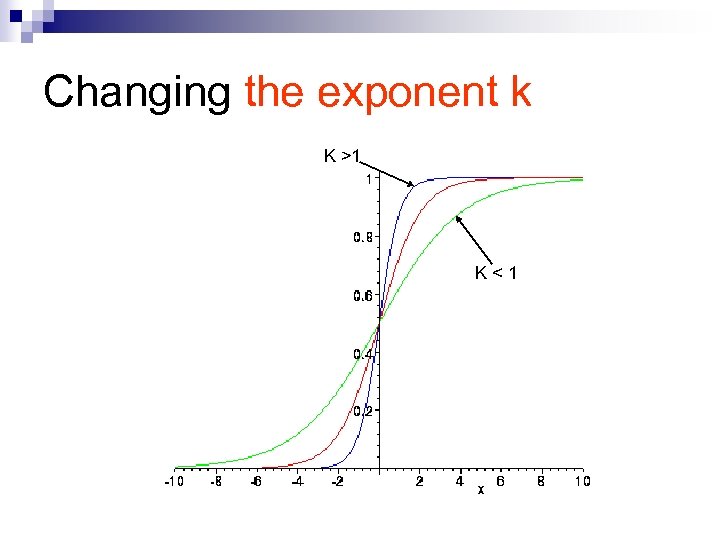Changing the exponent k K >1 K < 1

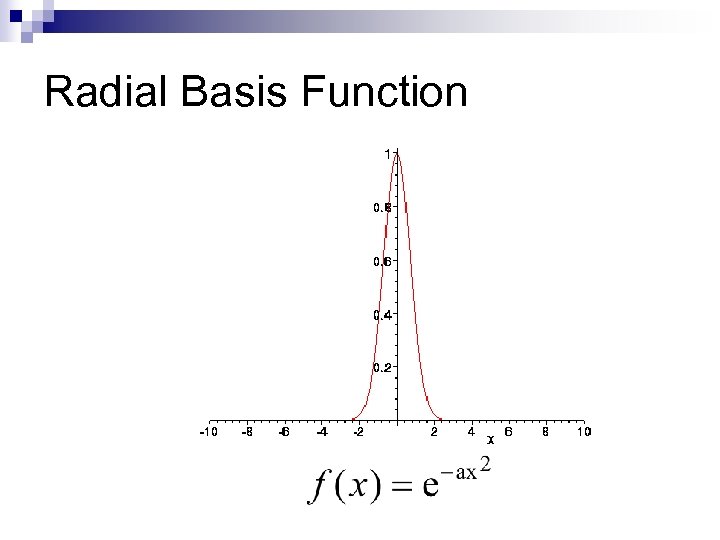Radial Basis Function

Stochastic units n Replace the binary threshold units by binary stochastic units that make biased random decisions. ¨ The “temperature” controls the amount of noise temperature

Types of Neuron parameters n n The form of the input function - e. g. linear, sigma-pi (multiplicative), cubic. The activation-output relation - linear, hardlimiter, or sigmoidal. The nature of the signals used to communicate between nodes - analog or boolean. The dynamics of the node - deterministic or stochastic.

Computing various functions n Mc. Collough-Pitts Neurons can compute logical functions. ¨ AND, NOT, OR

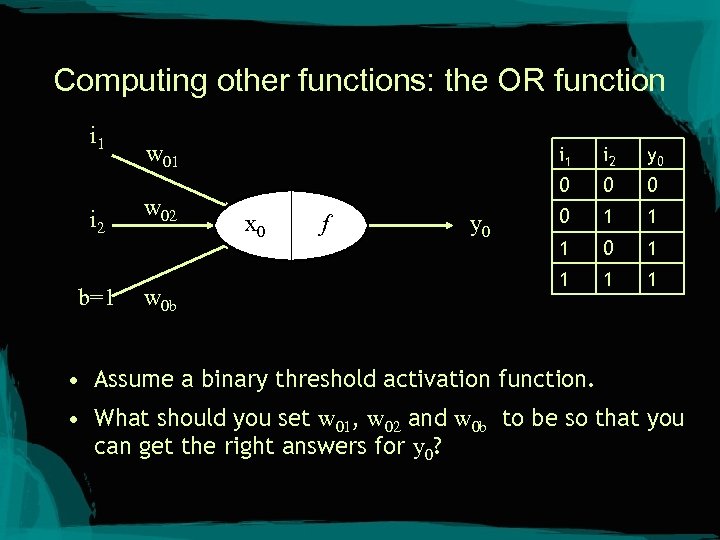Computing other functions: the OR function i 1 i 2 b=1 w 02 w 0 b i 1 f y 0 0 x 0 i 2 0 0 0 1 1 1 1 • Assume a binary threshold activation function. • What should you set w 01, w 02 and w 0 b to be so that you can get the right answers for y 0?

Many answers would work y = f (w 01 i 1 + w 02 i 2 + w 0 bb) i 2 recall the threshold function the separation happens when w 01 i 1 + w 02 i 2 + w 0 bb = 0 i 1 move things around and you get i 2 = - (w 01/w 02)i 1 - (w 0 bb/w 02)

Decision Hyperplane n n The two classes are therefore separated by the `decision' line which is defined by putting the activation equal to the threshold. It turns out that it is possible to generalise this result to TLUs with n inputs. In 3 -D the two classes are separated by a decision-plane. In n-D this becomes a decision-hyperplane.

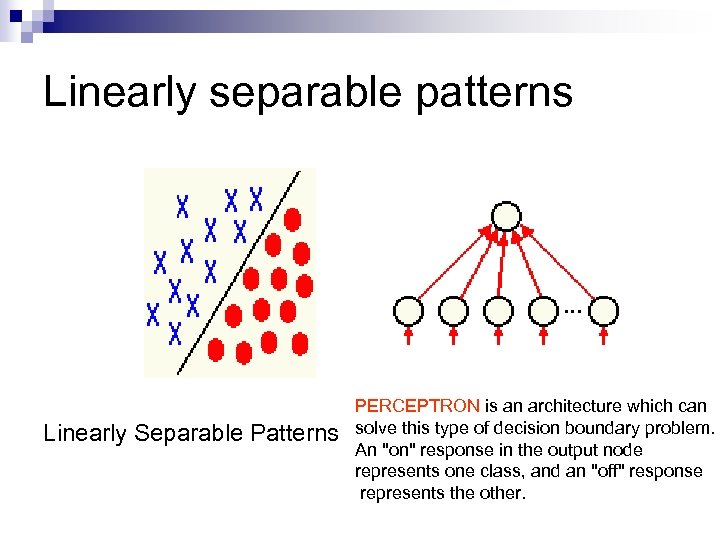Linearly separable patterns Linearly Separable Patterns PERCEPTRON is an architecture which can solve this type of decision boundary problem. An "on" response in the output node represents one class, and an "off" response represents the other.

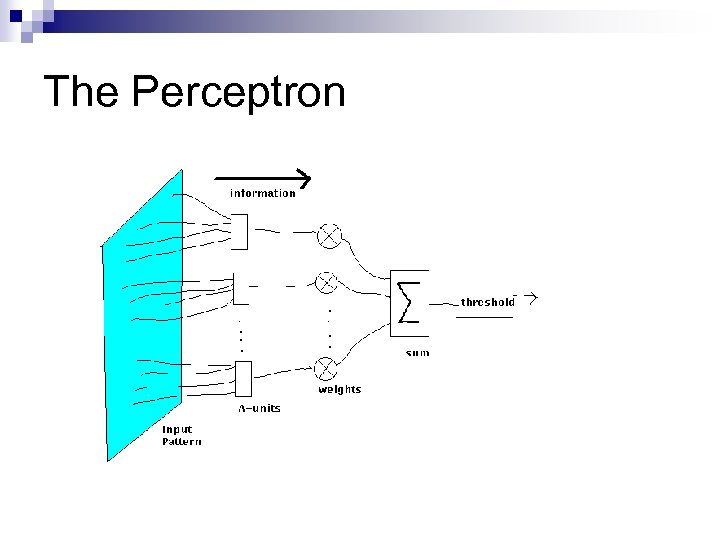The Perceptron

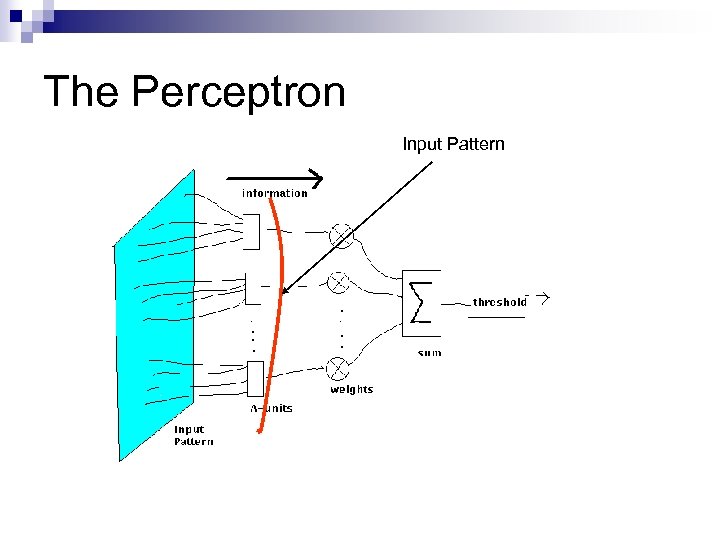The Perceptron Input Pattern

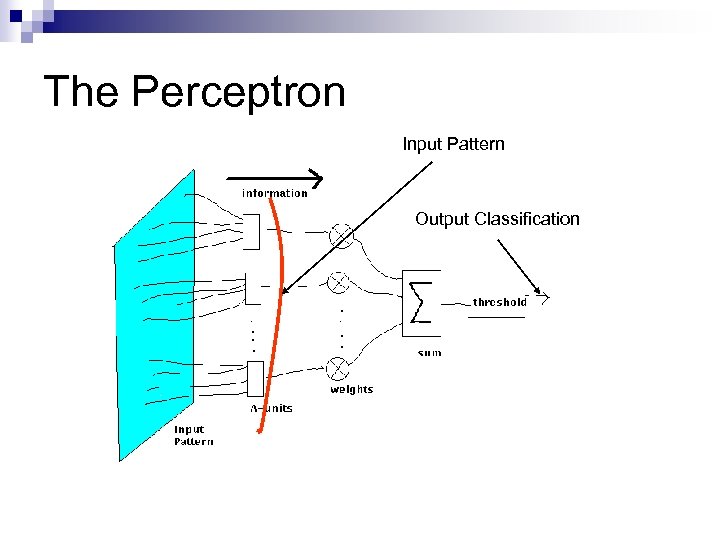The Perceptron Input Pattern Output Classification

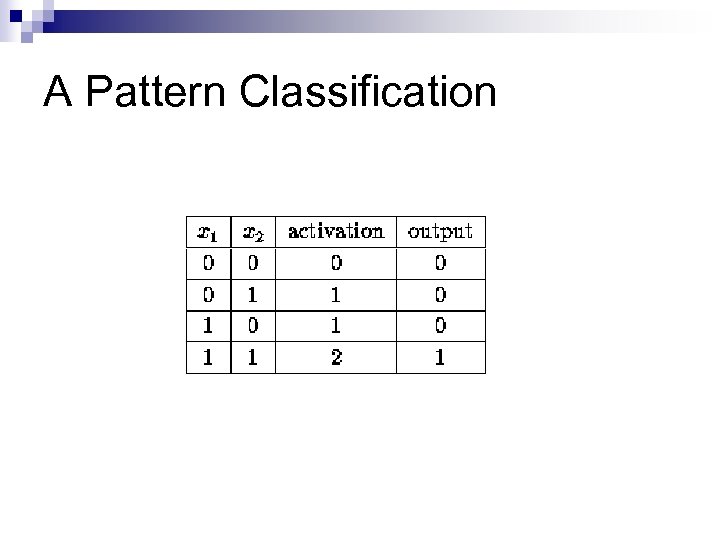A Pattern Classification

Pattern Space § The space in which the inputs reside is referred to as the pattern space. § Each pattern determines a point in the space by using its component values as space-coordinates. § In general, for n-inputs, the pattern space will be n-dimensional.

The XOR Function X 1/X 2 = 0 X 2 = 1 X 1= 0 0 1 X 1 = 1 1 0

The Input Pattern Space

The Decision planes From: S. Harris Computer Cartoons http: //www. sciencecartoonsplus. com/galcomp 2. htm

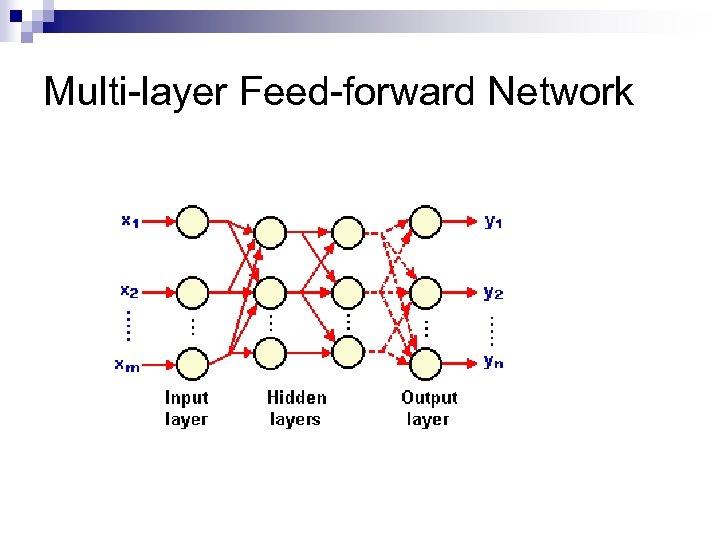Multi-layer Feed-forward Network

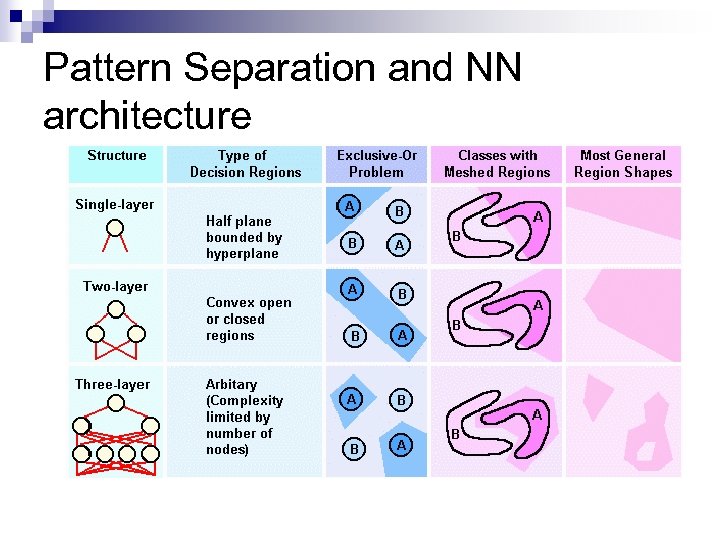Pattern Separation and NN architecture

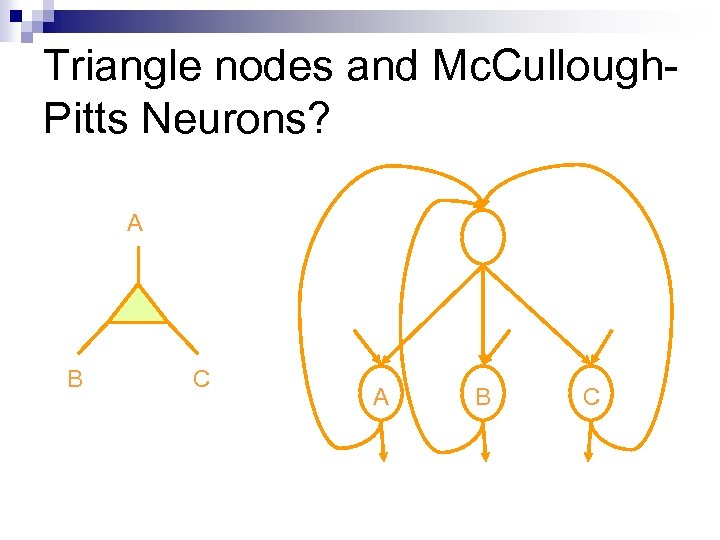Triangle nodes and Mc. Cullough. Pitts Neurons? A B C

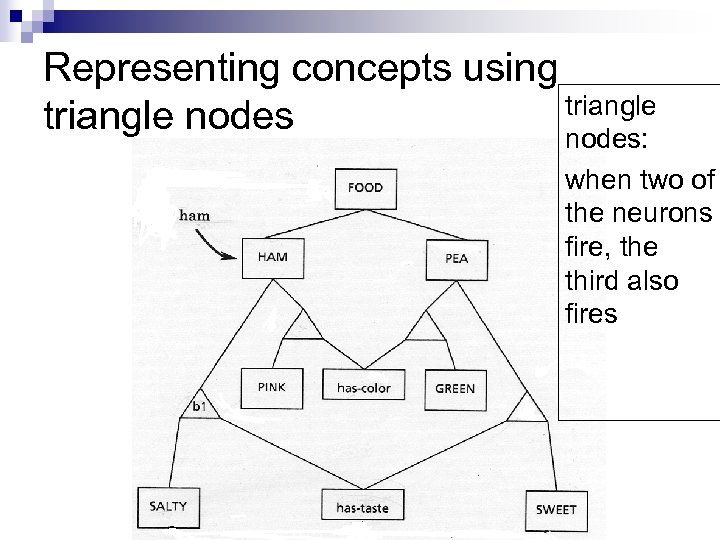Representing concepts using triangle nodes: when two of the neurons fire, the third also fires

Basic Ideas n n n Parallel activation streams. Top down and bottom up activation combine to determine the best matching structure. Triangle nodes bind features of objects to values Mutual inhibition and competition between structures Mental connections are active neural connections

Bottom-up vs. Top-down Processes Bottom-up: When processing is driven by the stimulus n Top-down: When knowledge and context are used to assist and drive processing n Interaction: The stimulus is the basis of processing but almost immediately topdown processes are initiated n

Stroop Effect n Interference between form and meaning

Name the words Book Car Table Box Trash Man Bed Corn Sit Paper Coin Glass House Jar Key Rug Cat Doll Letter Baby Tomato Check Phone Soda Dish Lamp Woman

Name the print color of the words Blue Green Red Yellow Orange Black Red Purple Green Red Blue Yellow Black Red Green White Blue Yellow Red Black Blue White Red Yellow Green Black Purple

Connectionist Model Mc. Clelland & Rumelhart (1981) n Knowledge is distributed and processing occurs in parallel, with bottom-up and top-down influences n This model can explain the Word-Superiority Effect because it can account for context effects

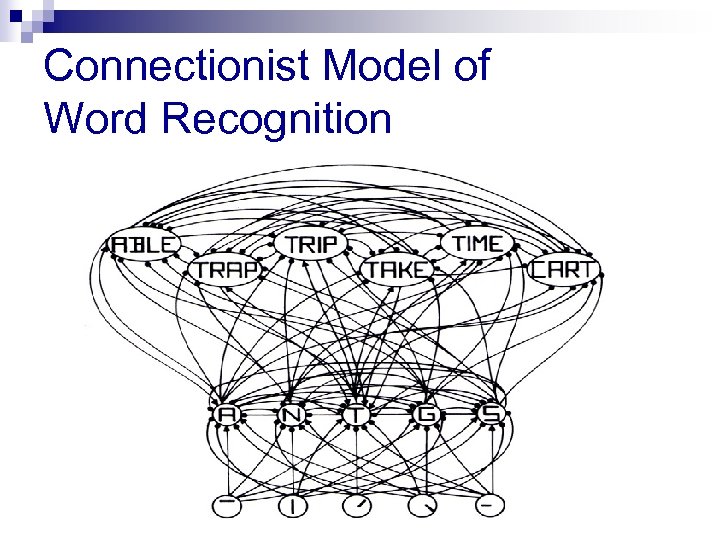Connectionist Model of Word Recognition

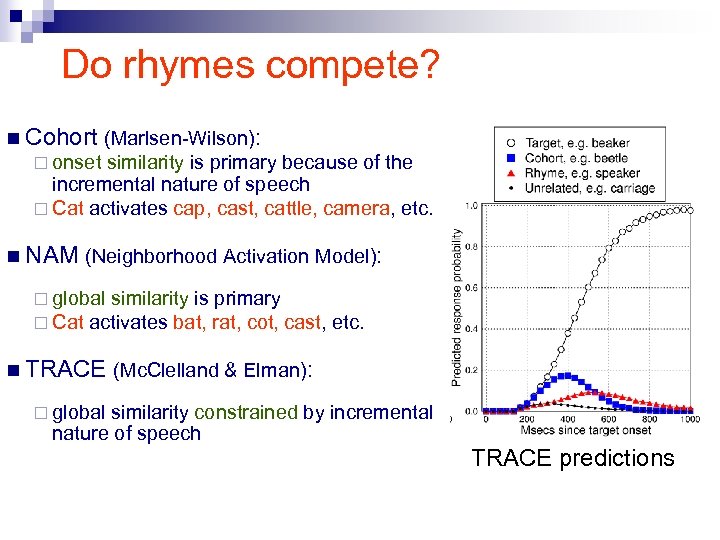Do rhymes compete? n Cohort (Marlsen-Wilson): ¨ onset similarity is primary because of the incremental nature of speech ¨ Cat activates cap, cast, cattle, camera, etc. n NAM (Neighborhood Activation Model): ¨ global similarity is primary ¨ Cat activates bat, rat, cot, cast, etc. n TRACE (Mc. Clelland & Elman): ¨ global similarity constrained by incremental nature of speech TRACE predictions

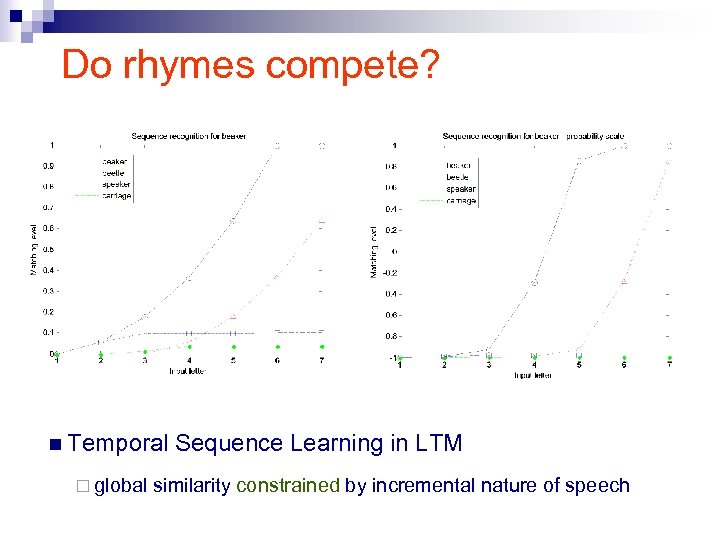Do rhymes compete? n Temporal Sequence Learning in LTM ¨ global similarity constrained by incremental nature of speech

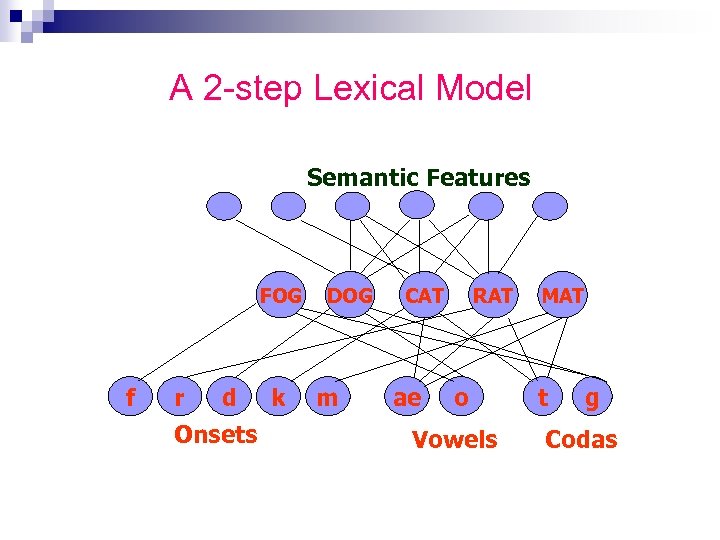A 2 -step Lexical Model Semantic Features FOG f r d Onsets k DOG m CAT ae RAT o Vowels MAT t g Codas

Linking memory and tasks From: S. Harris Computer Cartoons http: //www. sciencecartoonsplus. com/galcomp 2. htm

Distributed vs Local Representation John 0 0 John 1 0 0 1 1 0 Paul 0 1 0 0 George 0 0 1 1 George 0 0 1 0 Ringo n 1 Paul n 1 1 0 0 1 Ringo 0 0 0 1 What happens if you want to represent a group? How many persons can you represent with n bits? 2^n n n What happens if one neuron dies? How many persons can you represent with n bits? n

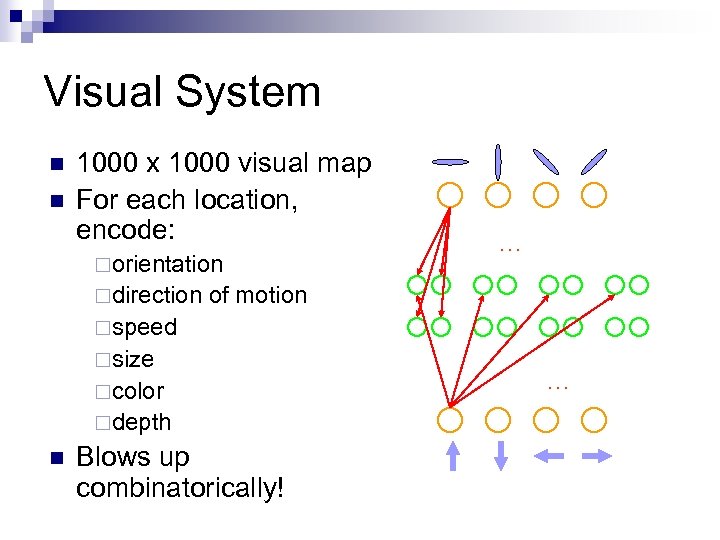Visual System n n 1000 x 1000 visual map For each location, encode: ¨orientation … ¨direction of motion ¨speed ¨size ¨color ¨depth n Blows up combinatorically! …

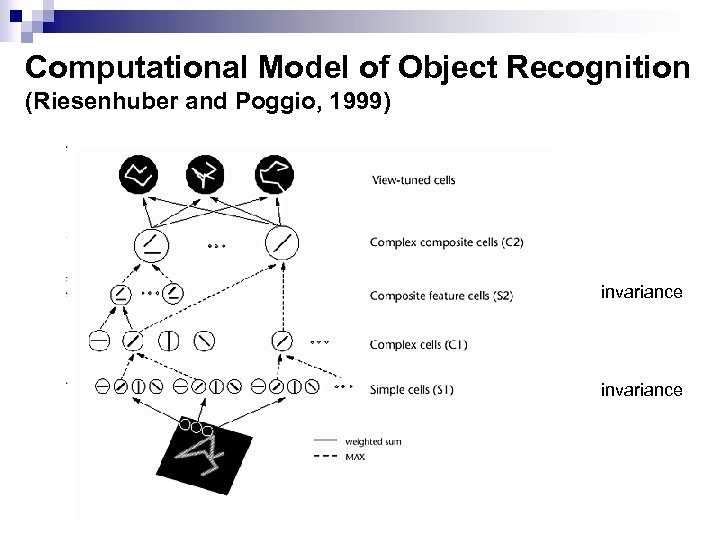Computational Model of Object Recognition (Riesenhuber and Poggio, 1999) invariance

Eye Movements: Beyond Feedforward Processing 1) Examine scene freely 2) estimaterial circumstances of family 3) give ages of the people 4) surmise what family has been doing before arrival of “unexpected visitor” 5) remember clothes worn by the people 6) remember position of people and objects 7) estimate how long the “unexpected visitor” has been away from family

How does activity lead to structural change? n n The brain (pre-natal, post-natal, and adult) exhibits a surprising degree of activity dependent tuning and plasticity. To understand the nature and limits of the tuning and plasticity mechanisms we study ¨ n How activity is converted to structural changes (say the ocular dominance column formation) It is centrally important to understand these mechanisms to arrive at biological accounts of perceptual, motor, cognitive and language learning ¨ Biological Learning is concerned with this topic.