33b4b23271bf7b4b8e9c04eab62f32d6.ppt
- Количество слайдов: 77
Motion Table of Contents Describing and Measuring Motion Slow Motion on Planet Earth Acceleration

Motion Learning Objectives 1. Determine when an object is in motion. • Key terms: reference point, relative motion, displacement 2. Calculate an object’s speed and velocity. • Key terms: average speed, instant speed, speed & direction, velocity 3. Demonstrate how to graph motion. • Key terms: slope = rise/run = rise divided by run = vertical movement divided by horizontal movement on a graph
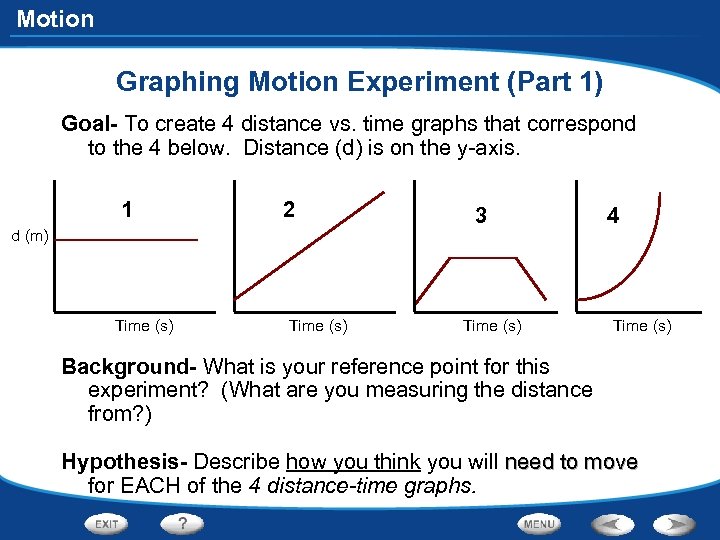
Motion Graphing Motion Experiment (Part 1) Goal- To create 4 distance vs. time graphs that correspond to the 4 below. Distance (d) is on the y-axis. 1 2 d (m) Time (s) 3 Time (s) 4 Time (s) Background- What is your reference point for this experiment? (What are you measuring the distance from? ) Hypothesis- Describe how you think you will need to move for EACH of the 4 distance-time graphs.

Motion Graphing Motion Experiment (Part 1) Results- Sketch your distance-time graphs and describe how you moved for each line segment of the graph. Conclusion- In complete sentences and using the motion sensor as your reference point, describe how you would move (or not move) for… 1. A horizontal line on a distance-time graph. 2. A slanted line going down and to the right on a distance-time graph. 3. A curved line curving up and to the right on a distance-time graph. 4. What happens to the slope of the graph if a person moves faster? 5. What does the graph look like if a person is moving at a constant rate or speed?

Motion Learning Objectives 1. Determine when an object is in motion. • Key terms: reference point, relative motion, displacement 2. Calculate an object’s speed and velocity. • Key terms: average speed, instant speed, speed & direction, velocity 3. Demonstrate how to graph motion and how to interpret the graph. • Key terms: slope = rise/run = rise divided by run = vertical movement divided by horizontal movement on a graph

Motion - Describing and Measuring Motion Determining When an Object is in Motion Have you ever watched a large truck pass you on the highway and felt like you were going backwards? Whether or not an object is in motion depends on the reference point you choose & if the distance between the object and the reference point is changing. Figure 2 - Page 8

Motion Negative Distance & Football Question: Can a distance be negative in relationship to a reference point? Football Example: Reference point in football (below), positive play (right), negative play- sacked for a loss (bottom right)

Motion Which of the following is true if you are riding your bike past the middle school? A. You are moving relative to the bike, but not the school. B. You are not moving relative to the school or the bike. C. You are moving relative to the school, but not relative to the bike. D. You are moving relative to the bike and the school.

Motion Suppose you are driving, and you are pulled over by a cop. The cop explains that his radar gun measured you as going 30 mph in a 65 mph zone. He also tells you that he used his radar gun while driving down the highway. Using physics, how do you get out of getting a ticket for driving too slowly? A. Explain that he graduated from Penns Valley. B. Explain that since he was moving, your speed is relative to his speed. This makes it seem like you were driving slowly. C. Explain that since he was moving, your speed is relative to his speed. This makes seem like you were driving fast. D. Explain that you never drive slowly. You always drive fast.

Motion How would a position-time graph appear for an object at that is not moving? A. B. C. D. A straight horizontal line A slanted line moving up and to the right. A curved line curving up and to the right. A slanted line moving down and to the left.
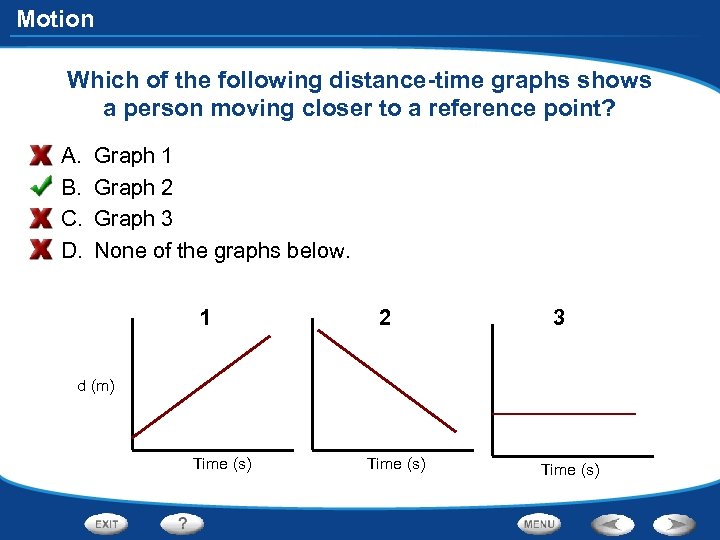
Motion Which of the following distance-time graphs shows a person moving closer to a reference point? A. B. C. D. Graph 1 Graph 2 Graph 3 None of the graphs below. 1 2 3 d (m) Time (s)
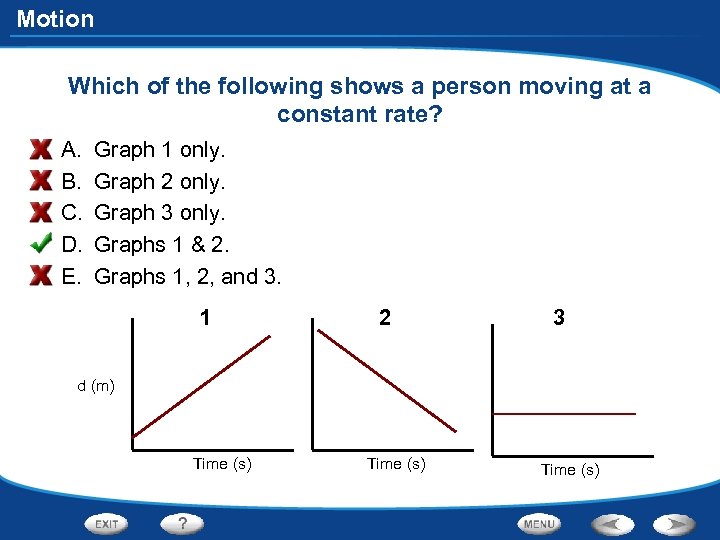
Motion Which of the following shows a person moving at a constant rate? A. B. C. D. E. Graph 1 only. Graph 2 only. Graph 3 only. Graphs 1 & 2. Graphs 1, 2, and 3. 1 2 3 d (m) Time (s)
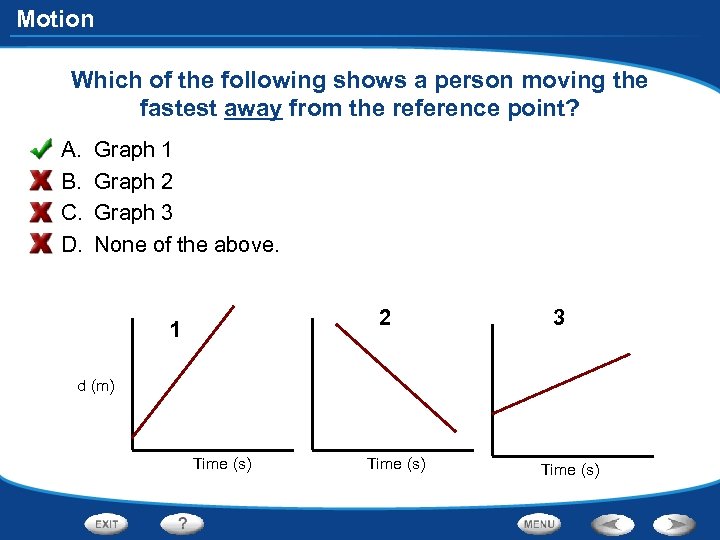
Motion Which of the following shows a person moving the fastest away from the reference point? A. B. C. D. Graph 1 Graph 2 Graph 3 None of the above. 2 1 3 d (m) Time (s)

Motion - Describing and Measuring Motion Calculating Speed What is an example of a speed that a fast car can go? So, how can you calculate speed? If you travel 45 km in 3 hours, what is your average speed? Speed = change in distance/change in time Instant speed is your speed at a certain time. Average speed is your averaged speed for the ENTIRE trial, event, or race. Avg. speed = change in distance/change in time

Motion Speed vs. Velocity Experiment Scenario (do not need to write): Markie is jogging at 6. 0 mph, while Suzy is also jogging at 6. 0 mph. However, Markie’s velocity is -6. 0 mph while Suzy’s is 6. 0 mph. Why are their speeds the same, but their velocities are different? Goal: Determine the difference between SPEED and VELOCITY. Hypothesis: What do you think is the difference between speed and velocity? General Procedure (Handheld procedure done as a group beforehand): 1. Using the velocity-time graph’s (x, y) coordinates at the top of the graph screen, determine each person’s VELOCITY while moving away from the motion sensor. Be sure to check if the velocity is positive or negative. 2. Using the velocity-time graph’s (x, y) coordinates at the top of the graph screen, determine each person’s VELOCITY when moving back toward the motion sensor. Be sure to check if the velocity is positive or negative. 3. Results: Organize the VELOCITIES FOR EACH PERSON in a DATA TABLE.

Motion Speed vs. Velocity Experiment Conclusion (answer in complete sentences): • Were there any negative velocities? Why is the case? Is velocity just speed? If not, what else is factored in to velocity? Hint- Think about when your velocity was negative relative to the motion sensor, and keep in mind that speed is NEVER negative. Scenario: Markie is jogging at a speed of 6. 0 mph, while Suzy is also jogging at a speed of 6. 0 mph. However, Markie’s velocity is -6. 0 mph while Suzy’s is 6. 0 mph. Why are their speeds the same, but their velocities are different? Velocity = speed + direction relative to a reference point So, Markie was going just as fast as Suzy, but in the opposite direction. Peregrine Falcons can dive at speeds up to 242 mph.
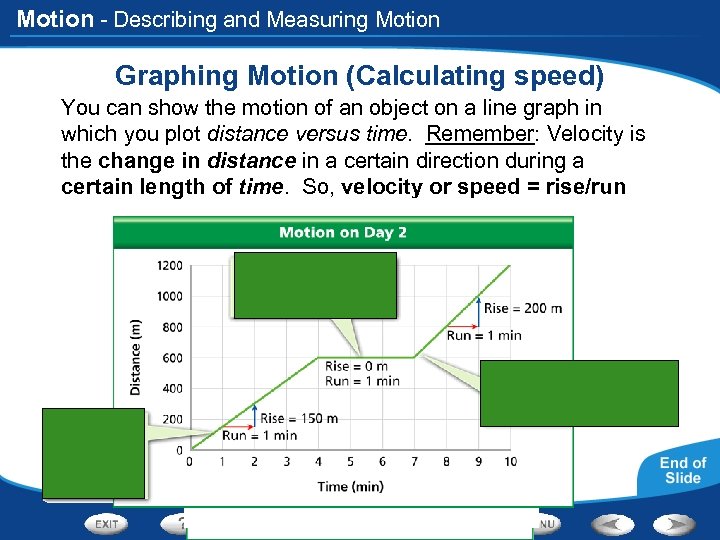
Motion - Describing and Measuring Motion Graphing Motion (Calculating speed) You can show the motion of an object on a line graph in which you plot distance versus time. Remember: Velocity is the change in distance in a certain direction during a certain length of time. So, velocity or speed = rise/run

Motion Graphing Motion Experiment (Part 2) In your lab notebook, match up each of the 4 distance-time graphs with one of the velocity graphs below. Sketch each of the graphs below and designate which velocity-time graph corresponds to which distance-time graph. Use your descriptions of speed or rate from Graphing Motion (Part 1) for help. BE SURE TO CAREFULLY ANALYZE WHAT HAPPENED TO DISTANCE & DIRECTION AND WHAT IS HAPPENING TO VELOCITY FOR THE DURATION OF DATA COLLECTION TIME FRAME! V = velocity A B C V (m/s) Time (s) D*
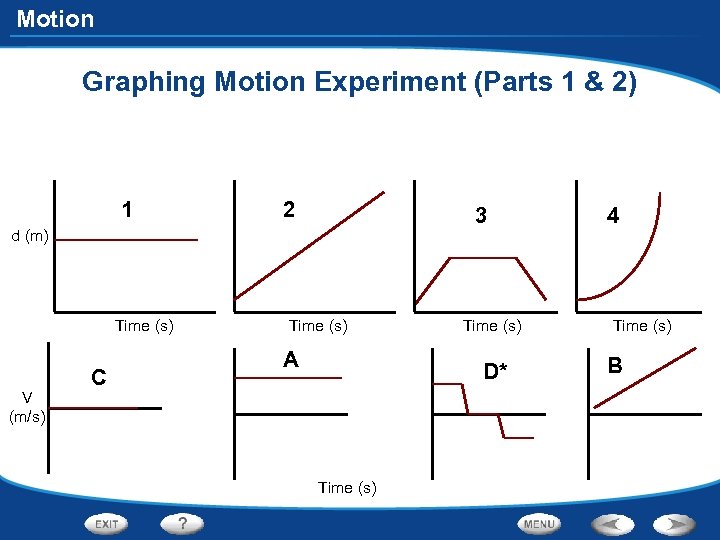
Motion Graphing Motion Experiment (Parts 1 & 2) 1 2 3 d (m) Time (s) V (m/s) C Time (s) A Time (s) D* Time (s) 4 Time (s) B

Motion Distance Determination (from a Speed-Time Graph) SPEED 5 m/s (m/s) 1 s 2 s Time (s) How far will the object have gone in 2 seconds? 10 meters (5 m/s x 2 s) Or Determine the area under the line: Create a rectangle and determine its area (l x w = 2 s x 5 m/s = 10 m)

Motion Jebediah runs 6 miles in 1 hour (60 minutes). His average speed is 6 mph. However, at minute 45, his speed was 4. 5 mph. Which of the following would best explain what happened? A. He was probably running faster at minute 45 than he was for most of the jog. B. He got more energy from drinking 5 Red Bulls before jogging. C. He was running up a hill and had to slow down. D. He wore out his running shoes.

Motion Explain what happened between 0 and 4 minutes in terms of the person’s speed. Keep in mind, the graph is a DISTANCE-TIME graph. A. B. C. D. The person moved at a constant speed The person stopped moving. The person slowed down. The person moved faster.
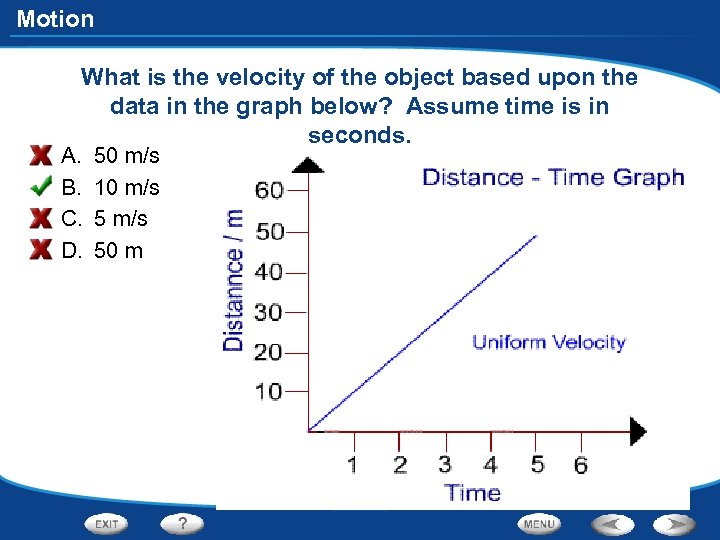
Motion What is the velocity of the object based upon the data in the graph below? Assume time is in seconds. A. B. C. D. 50 m/s 10 m/s 50 m

Motion How is velocity different from speed? A. Velocity involves instant and average speed, so it will be positive. B. Speed involves direction as well, so it can be negative. C. They’re the same. D. Velocity involves direction as well, so it can be negative.

Motion Which of the following may only be a measurement of speed? A. B. C. D. -0. 001 mm/s -2 m/s 27 mph 100 km/h East

Motion Which of the following is a measurement of velocity? A. B. C. D. 32 rpm (revolutions per minute) clockwise 100 km/h Northeast -2. 7 m/s All of the above.

Motion Suzy is moving East at a velocity of 7 mph from her house. Markie moved 14 miles West from Suzy’s house in 2 hours. What is Markie’s velocity? A. B. C. D. 7 mph -7 mph 6 mph East -6 mph

Motion If you are running at 5 mph, then how far will you run in 4 hours at the same pace? A. B. C. D. 25 miles 5 mph 20 miles 15 miles

Motion How far will the object go in 4 seconds (using the graph below)? A. B. C. D. 0 meters 4 meters 8 meters 12 meters SPEED (m/s) 2 m/s 2 s 4 s 6 s Time (s)

Motion Noggin Knockers from p. 15 - 1 a, 1 c, 2 b, 2 c, 3 a, & 3 b 1 c 2 c [9 points- Homework Grade] 1 - (a) Car- not moving (b) Road- not moving since the distance between you and the road is not changing; (c) Stop Sign- moving away or toward it. (1 point per part for 3 points total). 2 - Velocity = speed + direction (2 points) 3 - Slope and Speed = 600 meters/3 minutes = 200 m/min (2 points- 1 point for the correct value, 1 point for the correct units). 4 - Distance = Speed x time = area under the line = 10 m/s x 3 s = 30 m (2 points- 1 point for value, 1 point for correct units)

Motion Softball vs. Baseball Reaction Times Big Question: Is it tougher to hit a baseball than a softball? Baseball data: 95 mph fastball = 139. 33 ft/. sec. Distance from the pitcher’s mound = 60. 5 ft. Time it takes ball to get to the plate (t) = ? Set up a proportion (t = time): 1 sec. / 139. 33 ft. = t / 60. 5 ft. t =. 434 seconds *Note that it is slightly more time than the actual reaction time because the pitcher launches the ball about 5. 5 feet in front of the mound! Once this release point is taken into account, the reaction time is 0. 395 seconds.

Motion Softball vs. Baseball Reaction Times Big Question: Is it tougher to hit a baseball than a softball? Softball data: 72 mph softball = 105. 6 ft/. sec. Distance from the pitcher’s mound = 43 ft. Time it takes ball to get to the plate (t) = ? Set up a proportion (t = time): 1 sec. / 105. 6 ft. = t / 43 ft. t =. 407 seconds *Note that it is slightly more time than the actual reaction time because the pitcher launches the ball about 6 feet in front of the mound! Once this release point is taken into account, the reaction time is 0. 350 seconds.
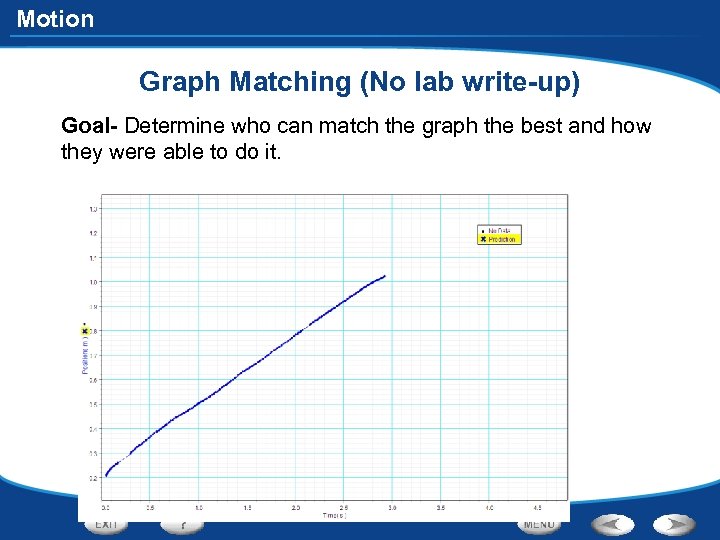
Motion Graph Matching (No lab write-up) Goal- Determine who can match the graph the best and how they were able to do it.

Motion End of Section: Describing and Measuring Motion

Motion - Slow Motion on Planet Earth’s Plates According to theory of plate tectonics, Earth’s landmasses have changed position over time because they are part of plates that are slowly moving.
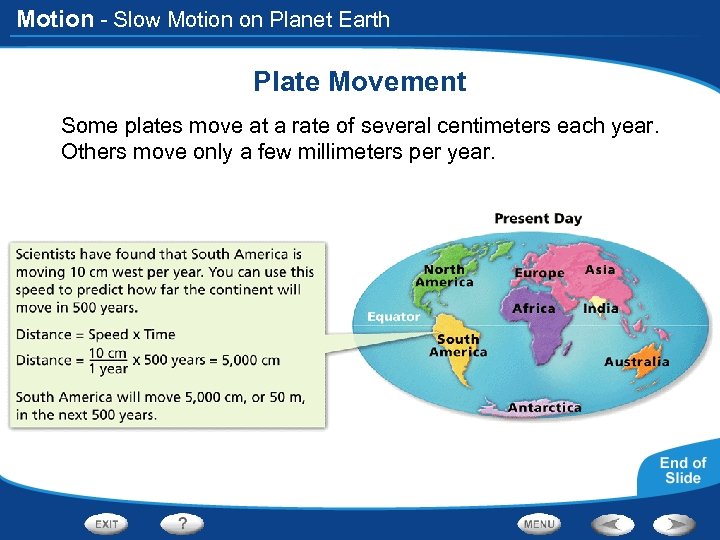
Motion - Slow Motion on Planet Earth Plate Movement Some plates move at a rate of several centimeters each year. Others move only a few millimeters per year.

Motion - Slow Motion on Planet Earth Continental Drift Activity Click the Active Art button to open a browser window and access Active Art about continental drift.

Motion - Slow Motion on Planet Earth Previewing Visuals Before you read, preview Figure 8. Then write two questions that you have about the diagram in a graphic organizer like the one below. As you read, answer your questions. Previewing Figure 8 Q. How have the positions of the continents changed over time? A. The distance between the continents has increased. Q. What causes Earth’s plates to move? A. Slow-moving currents beneath Earth’s outer layer cause the plates to move.

Motion End of Section: Slow Motion on Planet Earth

Motion Learning Objectives 1. Describe the motion of an object as it accelerates. • Key Terms: acceleration, change in velocity over time, increasing vs. decreasing speed, change in direction 2. Calculate acceleration. • Key Terms: change in velocity over time 3. Describe how graphs are used to analyze the motion of an accelerating object. • Key Terms: Velocity vs. Time graph, Distance vs. Time Graph, slope

Motion - Acceleration Calculating Acceleration What does it mean if a car accelerates? Have you ever heard of a car that can go 0 to 60 mph in about 6 seconds? (Just like mine). What about when a car decelerates? To determine the acceleration of an object moving in a straight line, you must calculate the change in velocity per unit of time Average Acceleration = (final velocity – starting velocity)/time
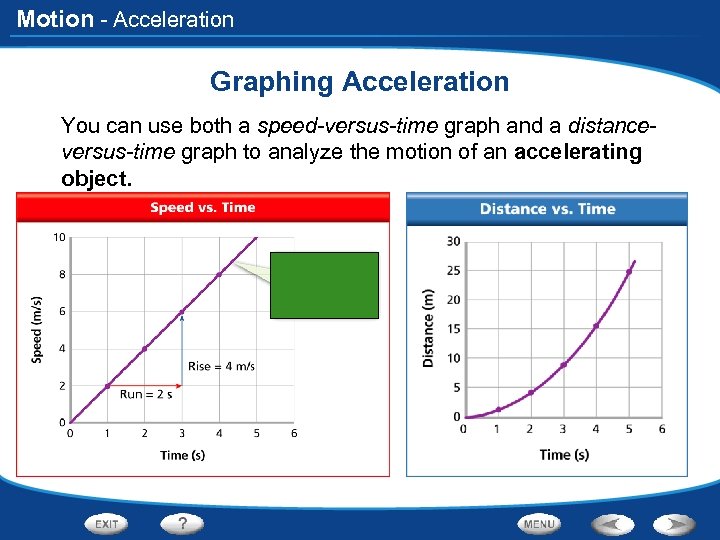
Motion - Acceleration Graphing Acceleration You can use both a speed-versus-time graph and a distanceversus-time graph to analyze the motion of an accelerating object.
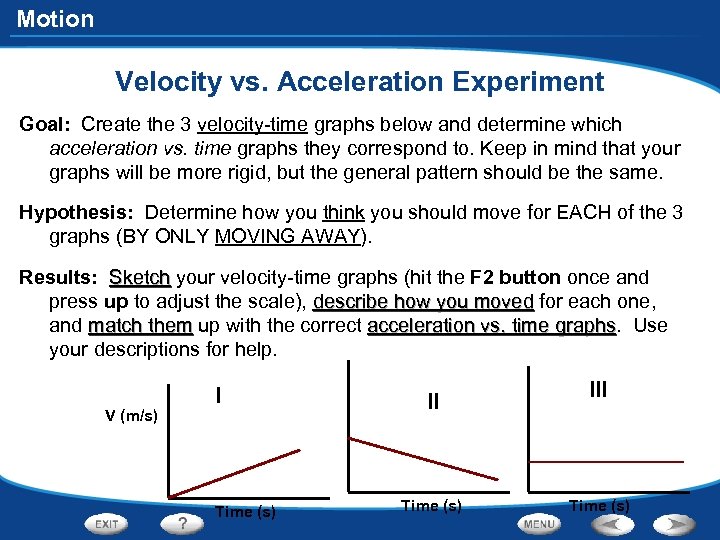
Motion Velocity vs. Acceleration Experiment Goal: Create the 3 velocity-time graphs below and determine which acceleration vs. time graphs they correspond to. Keep in mind that your graphs will be more rigid, but the general pattern should be the same. Hypothesis: Determine how you think you should move for EACH of the 3 graphs (BY ONLY MOVING AWAY). Results: Sketch your velocity-time graphs (hit the F 2 button once and press up to adjust the scale), describe how you moved for each one, and match them up with the correct acceleration vs. time graphs. Use graphs your descriptions for help. V (m/s) I Time (s) III Time (s)

Motion Velocity vs. Acceleration Experiment A (m/s 2) 0 A B 0 C 0 Time (s) Conclusion (answer in complete sentences): 1. How did you move for 0 or no acceleration? 2. How did you move for a constant positive acceleration? 3. How did you move for a constant negative acceleration (or deceleration)? 4. What is the independent or manipulated variable for the graphs above? What is the dependent or responding variable for the graphs above? Also, note which axis (x or y) the variables are on.
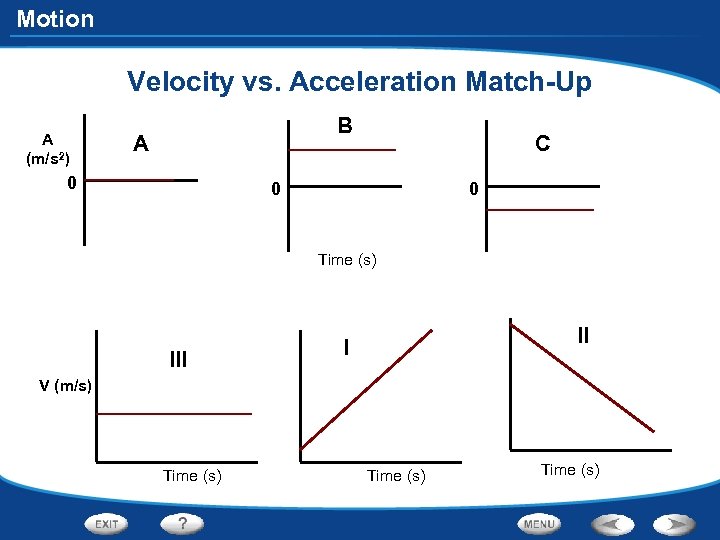
Motion Velocity vs. Acceleration Match-Up A (m/s 2) B A 0 C 0 0 Time (s) III II I V (m/s) Time (s)

Motion Learning Objectives 1. Describe the motion of an object as it accelerates. • Key Terms: acceleration, change in velocity over time, increasing vs. decreasing speed, change in direction 2. Calculate acceleration. • Key Terms: change in velocity over time 3. Describe how graphs are used to analyze the motion of an accelerating object. • Key Terms: Velocity vs. Time graph, Distance vs. Time Graph, slope
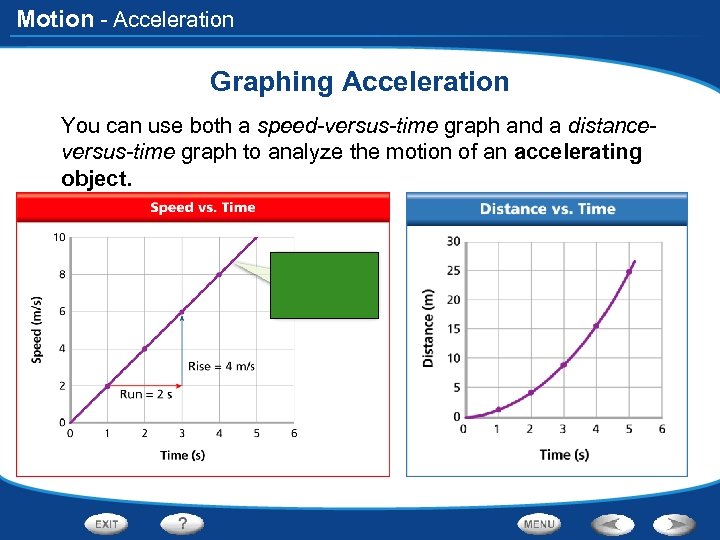
Motion - Acceleration Graphing Acceleration You can use both a speed-versus-time graph and a distanceversus-time graph to analyze the motion of an accelerating object.
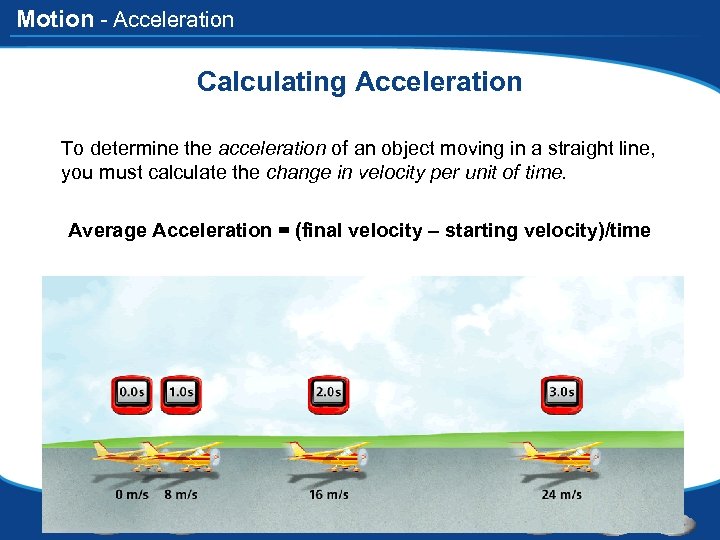
Motion - Acceleration Calculating Acceleration To determine the acceleration of an object moving in a straight line, you must calculate the change in velocity per unit of time. Average Acceleration = (final velocity – starting velocity)/time

Motion - Acceleration Calculating Acceleration As a roller-coaster car starts down a slope, its speed is 4 m/s. But 3 seconds later, at the bottom, its speed is 22 m/s. What is its average acceleration? Read and Understand What information have you been given? Initial speed = 4 m/s Final Speed = 22 m/s Time = 3 s

Motion - Acceleration Calculating Acceleration As a roller-coaster car starts down a slope, its speed is 4 m/s. But 3 seconds later, at the bottom, its speed is 22 m/s. What is its average acceleration? Plan and Solve What quantity are you trying to calculate? The average acceleration of the roller-coaster car = __ What formula contains the given quantities and the unknown quantity? Acceleration = (Final speed – Initial speed)/Time Perform the calculation. Acceleration = (22 m/s – 4 m/s)/3 s = 18 m/s/3 s Acceleration = 6 m/s 2 The roller-coaster car’s average acceleration is 6 m/s 2. This is a positive acceleration (speeding up).

Motion - Acceleration Calculating Acceleration As a roller-coaster car starts down a slope, its speed is 4 m/s. But 3 seconds later, at the bottom, its speed is 22 m/s. What is its average acceleration? Look Back and Check Does your answer make sense? The answer is reasonable. If the car’s speed increases by 6 m/s each second, its speed will be 10 m/s after 1 second, 16 m/s after 2 seconds, and 22 m/s after 3 seconds.

Motion - Acceleration Calculating Acceleration Practice Problem A certain car brakes from 27 m/s to rest in 9 seconds. Find the car’s average acceleration. (0 m/s – 27 m/s ) ÷ 9 s = -27 m/s ÷ 9 s = -3 m/s 2 This is a negative acceleration, which is also called a deceleration (slowing down)

Motion Acceleration Practice Problems: Determine Each Object’s Acceleration 1. A car travels at 28 m/s (a little over 60 mph) and stops at a red light in 4 seconds. 2. A person starts jogging at 6 km/h and ends up jogging at 10 km/h in 30 minutes. You may need to convert units. 3. Your car goes from rest to 30 m/s in half a minute.

Motion Noggin Knockers

Motion Noggin Knockers

Motion Noggin Knockers

Motion Learning Objectives 1. Describe the motion of an object as it accelerates. • Key Terms: acceleration, change in velocity over time, increasing vs. decreasing speed, change in direction 2. Calculate acceleration. • Key Terms: change in velocity over time 3. Describe how graphs are used to analyze the motion of an accelerating object. • Key Terms: Velocity vs. Time graph, Distance vs. Time Graph, slope

Motion Changing Directions When riding in a car, have you ever changed directions by going around a curve or turn in the road at a “high” speed? Did you feel your body push towards the outside of the curve? Another example would be riding on those amusement park rides that spin around quickly. This is an acceleration too (Centripetal Acceleration = the object you’re in is being pulled towards the middle of the circle while you feel pushed toward the outside of the circle).

Motion Which of the following is not an example of a positive or negative acceleration? A. Going from jogging to running during the last 30 seconds of a 5 K race. B. Jebediah rides his horse and buggy at a constant speed of 5 mph for an entire 10 minutes on a straight road. C. A car braking due to traffic. D. A car turning around on the highway.

Motion Which of the following is an example of a positive acceleration? A. A bus coming to a stop. B. A car peeling out of the parking lot like Mr. Snyder on Fridays at 3: 15 PM. C. A rollercoaster braking. D. A person standing still.

Motion Which of the following is an example of a negative acceleration? A. B. C. D. A skateboarder taking off from rest to a speed of 5 m/s. A truck going at a constant speed of 65 mph. A bus coming to a stop after a tractor stops in front of it. A car speeding up in the passing lane.

Motion Which of the following is an example of 0 or no acceleration? A. B. C. D. A bowling ball slowing down when it hits the 10 pins. A car speeding up to pass another vehicle. A bus coming to a stop. A person riding a bike at 15 mph for 2 hours on a straight path because there is nothing better to do in Bald Eagle.
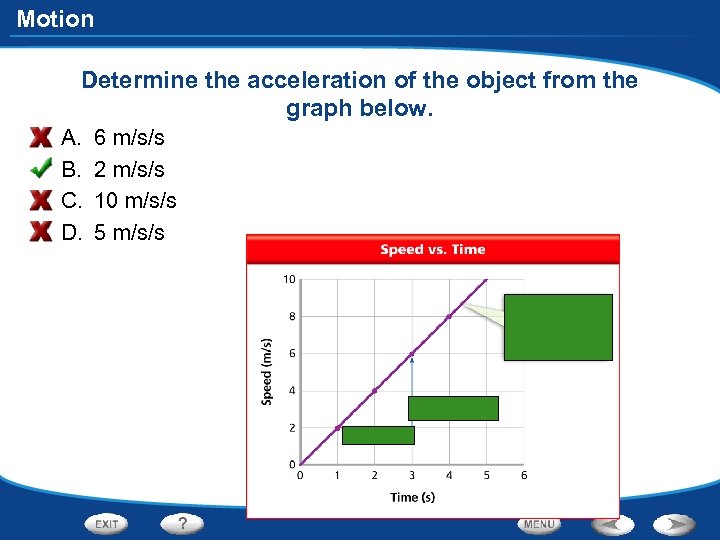
Motion Determine the acceleration of the object from the graph below. A. B. C. D. 6 m/s/s 2 m/s/s 10 m/s/s 5 m/s/s

Motion If you measure velocity in miles per hour and time in hours, then what would be the units for acceleration? A. B. C. D. Miles per hour (Miles/h/h or Miles/hr/hr) Miles per hour (mph) Hours (h or hr) Hours squared per mile (hr 2/mile)

Motion Determine the acceleration if a roller coaster starts from rest and reaches a speed of 27 m/s in 3 seconds. A. B. C. D. 9 m/s or 9 mps -81 m/s/s or -81 m/s 2 9 m/s/s or 9 m/s 2 -9 m/s/s or -9 m/s 2

Motion A roller coaster goes from a speed of 27 m/s to rest in 3 seconds. What is the rollercoaster’s acceleration? A. B. C. D. 9 m/s or 9 mps -81 m/s/s or 81 m/s 2 9 m/s/s or 9 m/s 2 -9 m/s/s or -9 m/s 2

Motion A car is traveling at 20 mph and after 10 seconds, the car is moving at 20 mph. What is its average acceleration? A. B. C. D. -2 m/s/s or -2 m/s 2 2 m/s/s or 2 m/s 2 0 m/s/s or 0 m/s 2 It cannot be calculated.

Motion Markie is riding the Tilt-a-Whirl at an amusement park. He is spinning around at a constant speed of 4 m/s. Which of the following is true? A. He never accelerates during the entire ride. B. His ride car accelerates towards the inside of the circular spin. C. He decelerates as the ride spins around. D. He will get sick while on the ride.

Motion Noggin Knockers (7 points)p. 27: 1 a, 1 c, 2 b, 3 c, 4 1 (2 points)- The skater is accelerating by changing direction/spinning/going in a circular pattern. 2 (2 points)- (15 m/s – 0 m/s)/10 seconds = 1. 5 m/s/s 3 (1 point)- Object is decelerating/negatively accelerating/slowing down 4 (2 points)- (9 m/s – 18 m/s)/3 seconds = -3 m/s/s

Motion Velocity vs. Acceleration Extension Goal- Create the velocity-time graphs below and describe how you moved for each one. Time (s) 0 V (m/s) IV V VI Procedure Help: Switch to Velocity-time graph and use the F 2 and up buttons to “stretch” the graph to the appropriate scale. Conclusion (in complete sentences): What was the main difference with your motion in the creation of the graphs in this experiment compared to the ones in the Velocity vs. Acceleration Experiment?

Motion Practice Test 1. If the distance between that object and the reference pt. is changing. 2. Sidewalk- not moving; tree-moving 3. To be drawn 4. 100 m/20 s = 5 m/s 5. No 6. Speed and direction 7. To be drawn 8. Acceleration 9. Slowing down- running then stopping, approaching a red light, etc.

Motion Practice Test (Continued) 10. Velocity units = m/s, time units = seconds 11. Acceleration 12. Speed or velocity 13. Slowing down 14. 1 minute = 60 seconds; (120 m/s – 60 m/s)/60 s = 1 m/s/s 15. To be drawn 16. Man. /Ind. variable (x-axis) = time; Res. /Dep/ variable (yaxis) = distance 17. Rise/Run, determine the slope of the line 18. 3 m/s x 5 s = 15 meters 19. (0 m/s – 20 m/s)/5 s = -20 m/s divided by 5 s = -4 m/s/s

Motion - Acceleration Identifying Main Ideas As you read the section “What is Acceleration? ”, write the main idea in a graphic organizer like the one below. Then write three supporting details that further explain the main idea. Main Idea In science, acceleration refers to. . . Detail Increasing speed Detail Decreasing speed Detail Changing direction

Motion - Acceleration Links on Acceleration Click the Sci. Links button for links on acceleration.

Motion End of Section: Acceleration
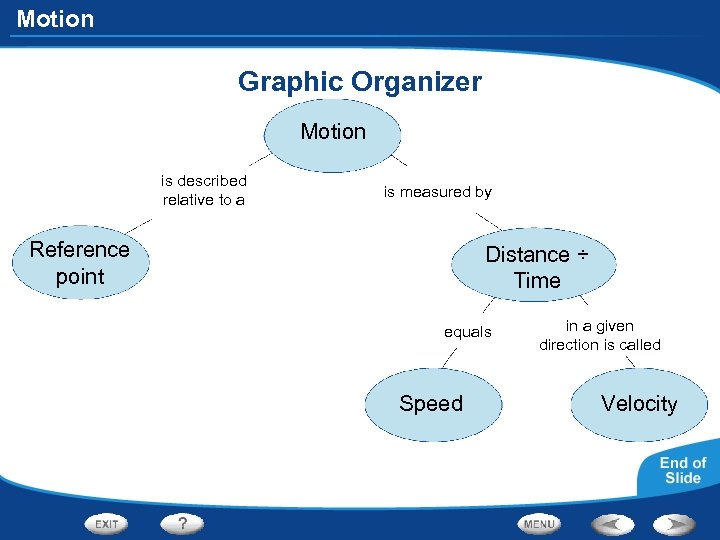
Motion Graphic Organizer Motion is described relative to a is measured by Reference point Distance ÷ Time equals Speed in a given direction is called Velocity

Motion End of Section: Graphic Organizer
33b4b23271bf7b4b8e9c04eab62f32d6.ppt