Московский Физико-Технический Институт Оптимизация методов умножения матриц библиотеки линейной алгебры для ВК “Эльбрус-3 M 1” и “Эльбрус-90 микро” Выполнил: Чернилевский Д. А. Научный руководитель: Логинов В. Е. 2009 г.
Разделы библиотеки EML.
Структура раздела Algebra (библиотека BLAS): l BLAS: y = αx + y l y = αAx + βy l C = αAB + βC A и В – матрицы, х и у – вектора, α и β – числа.
Цель работы l Провести анализ существующей реализации библиотеки EML l Выявить возможные способы оптимизации кода с применением архитектурных особенностей ВК “Эльбрус-90 микро” и “Эльбрус-3 М 1” l Провести оптимизацию функций умножения матриц, основываясь на проведенном анализе
Оптимизации функций умножения матриц для “Эльбрус-90 микро” l Разбиение матриц на блоки l Применение оптимизации unroll к исходным текстам l Устранение зависимостей между итерациями циклов l Использование последовательного чтения/записи из/в память l Вынос нелинейных индексов массивов за пределы цикла
Разбиение матриц на блоки Причины оптимизации: - Отсутствие устройства предподкачки - Размер L 1$: 32 kb Решение: - Поблочное умножение *TRMM – Умножение треуг. матриц, GEMM – Умножение прямоуг. матриц
Применение оптимизации unroll к исходным текстам и последовательное обращение в память Цели: - Устранение зависимостей за счет применения оптимизации unroll к внешнему циклу - Улучшение загрузки конвейера за счет независимости операций в цикле после оптимизации unroll - Уменьшение количества запросов в память за счет многократного использования элементов матрицы - Эффективное использование поблочной загрузки и записи в память for (i = 0; i < M - 3; i += 4) { a 0 = (eml_32 f *) A; b 1 = b 0 + ldb; b 2 = b 1 + ldb; b 3 = b 2 + ldb; for (j = 0; j < N; j++) { t 0 = t 1 = t 2 = t 3 = 0; l = j; #pragma unroll (2) for (; l < K; l++) { t 0 += b 0[l] * a 0[l * lda]; t 1 += b 1[l] * a 0[l * lda]; t 2 += b 2[l] * a 0[l * lda]; t 3 += b 3[l] * a 0[l * lda]; } C[j] += alpha * t 0; C[ldc + j] += alpha * t 1; C[2 * ldc + j] += alpha * t 2; C[3 * ldc + j] += alpha * t 3; a 0 += 1; } C += 4 * ldc; b 0 += 4 * ldb; }
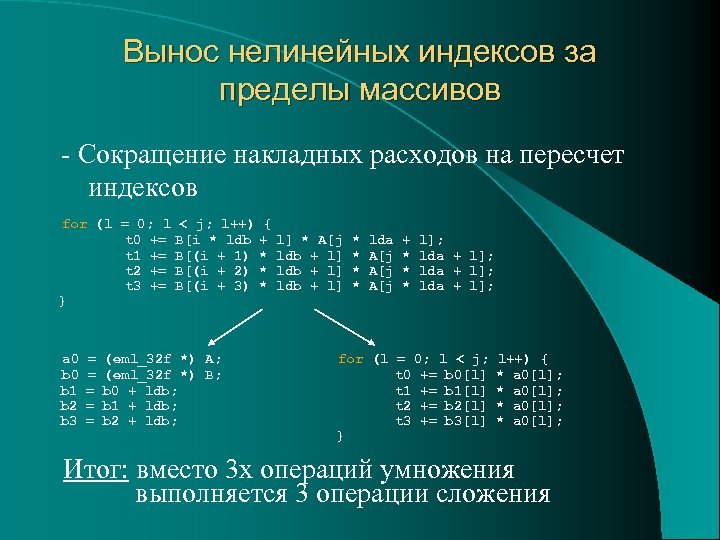
Вынос нелинейных индексов за пределы массивов - Сокращение накладных расходов на пересчет индексов for (l = 0; l < j; l++) { t 0 += B[i * ldb + l] * A[j * lda + l]; t 1 += B[(i + 1) * ldb + l] * A[j * lda + l]; t 2 += B[(i + 2) * ldb + l] * A[j * lda + l]; t 3 += B[(i + 3) * ldb + l] * A[j * lda + l]; } a 0 = (eml_32 f *) A; b 0 = (eml_32 f *) B; b 1 = b 0 + ldb; b 2 = b 1 + ldb; b 3 = b 2 + ldb; for (l = 0; l < j; l++) { t 0 += b 0[l] * a 0[l]; t 1 += b 1[l] * a 0[l]; t 2 += b 2[l] * a 0[l]; t 3 += b 3[l] * a 0[l]; } Итог: вместо 3 х операций умножения выполняется 3 операции сложения
Особенности архитектуры “Эльбрус-3 М 1”, существенные при проведении оптимизаций l Наличие векторных инструкций l Конвейеризация l Асинхронный циклов доступ к массивам (наличие APB) l АЛУ: 2 кластера по 3 канала
Оптимизации функций умножения матриц для “Эльбрус-3 М 1” l Разбиение матриц на блоки – нет необходимости из-за наличия APB l Применение оптимизации unroll к исходным текстам l Устранение зависимостей между итерациями циклов l Использование последовательного чтения/записи из/в память – нет необходимости из-за наличия APB l Использование векторных инструкций l Подбор состава операций для максимальной загрузки АЛУ
Использование векторных инструкций и подбор состава операций Цели: - Обработка нескольких элементов матрицы за такт - Максимальная загрузка АЛУ Проблемы: - Необходимость выравнивания данных в памяти по границе 64 х битных слов … t 10 = alpha * A[(i + 1) * lda + l]; t 11 = alpha * A[(i + 1) * lda + l + 1]; t 12 = alpha * A[(i + 1) * lda + l + 2]; t 13 = alpha * A[(i + 1) * lda + l + 3]; … tmp 10 = e 3 m_pshufh (*((eml_32 s *) & t 10), 0 x 44); tmp 11 = e 3 m_pshufh (*((eml_32 s *) & t 11), 0 x 44); tmp 12 = e 3 m_pshufh (*((eml_32 s *) & t 12), 0 x 44); tmp 13 = e 3 m_pshufh (*((eml_32 s *) & t 13), 0 x 44); for (j = 0; j < N >> 1; j++) { … s. C 1[j] = e 3 m_pfadds (s. C 1[j], e 3 m_pfmuls (tmp 10, s. B 0[j])); s. C 1[j] = e 3 m_pfadds (s. C 1[j], e 3 m_pfmuls (tmp 11, s. B 1[j])); s. C 1[j] = e 3 m_pfadds (s. C 1[j], e 3 m_pfmuls (tmp 12, s. B 2[j])); s. C 1[j] = e 3 m_pfadds (s. C 1[j], e 3 m_pfmuls (tmp 13, s. B 3[j])); … }
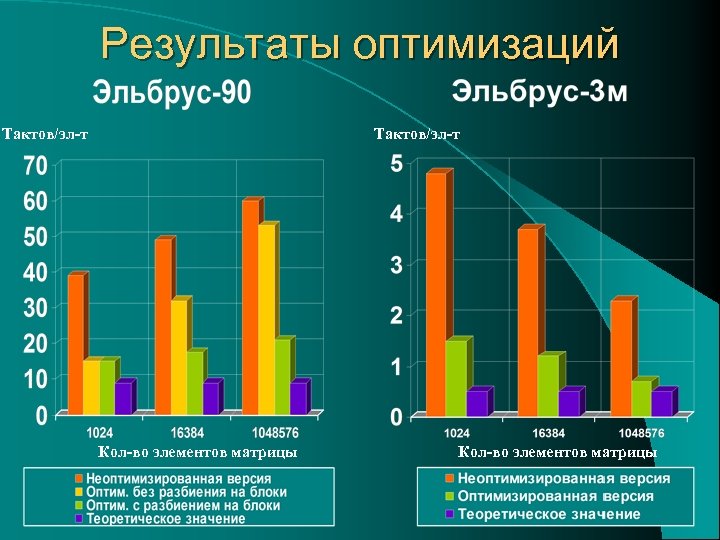
Результаты оптимизаций Тактов/эл-т Кол-во элементов матрицы
Заключение l Оптимизированы функции умножения матриц: умножение треугольных матриц различных конфигураций (слева – справа, верхнетреугольные – нижнетреугольные, транспонированные – не транспонированные) для различных типов данных (32 F, 32 FC, 64 FC). Всего около 60 функций. l Проведено функциональное тестирование l Проведено измерение производительности l Получен прирост производительности в среднем в 2 -4 раза по сравнению с изначальными алгоритмами библиотеки BLAS, не использующими особенности ВК “Эльбрус-90 микро” и “Эльбрус-3 М 1”
Скачать презентацию Московский Физико-Технический Институт Оптимизация методов умножения матриц библиотеки
43dd8a06da9a5c5d09392d65f9e765eb.ppt