Московский энергетический институт Кафедра Вычислительных машин систем и

Московский энергетический институт Кафедра Вычислительных машин систем и сетей Моё направление: «Проблемы организации высокоточных вычислений» Лекция на тему: «Применение модулярной арифметики в высокоточных вычислениях» Москва 2013 г.

Обобщенный модулярный формат представления вещественных чисел Любое вещественное число А в формате с фиксированной точкой можно представить в виде: Пример: или: Модулярный формат представления А имеет вид: где длина целой части числа с фиксированной точкой, длина дробной части числа с фиксированной точкой, порядок А где – целые числа – модули. остаток от деления числа на целое число такое, что … Условие выбора модулей: . t

Правила выполнения арифметических операций в модулярном формате Входные данные: и Сложение Шаг № 1. Вычисляем: Шаг № 2. Порядок результата равен большему порядку чисел Вычитание и Шаг № 1. Вычисляем: Шаг № 2. Порядок результата равен большему порядку чисел и Умножение Шаг № 1. Вычисляем: Шаг № 2. Порядок результата равен сумме порядков чисел. и Достоинством модулярной системы счисления является отсутствие переносов между модулями, что позволяет распараллелить процесс выполнения арифметических операций и ускорить высокоточные вычисления. Недостатком: сложность округления и деление чисел только на константы.

Обобщенное представление комплексных чисел в модулярном формате Любое комплексное число А в формате с фиксированной точкой можно представить в виде: или где целое комплексное число такое, что: Для представления комплексных чисел в модулярной системе счисления должно выполняться неравенство:

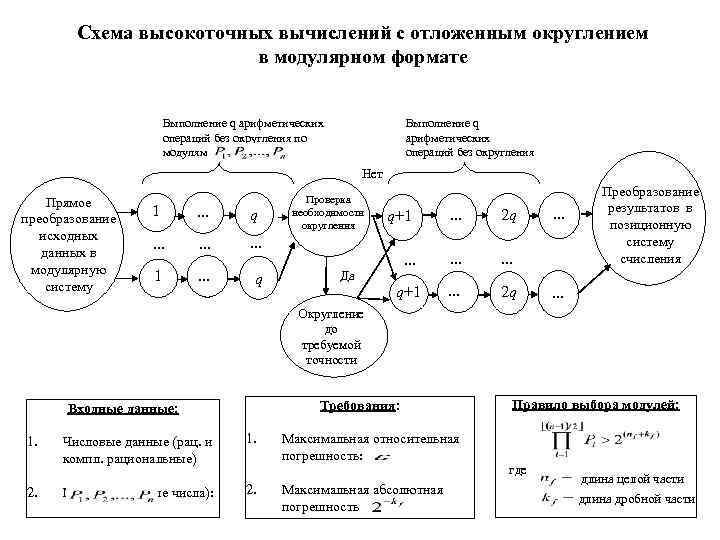Схема высокоточных вычислений с отложенным округлением в модулярном формате Выполнение q арифметических операций без округления по модулям Выполнение q арифметических операций без округления Нет Прямое преобразование исходных данных в модулярную систему 1 . . . q . . 1 . . . q Проверка необходимости округления q+1 . . . 2 q . . . Да Преобразование результатов в позиционную систему счисления . . . Округление до требуемой точности Требования: Входные данные: 1. 2. Числовые данные (рац. и компл. рациональные) 1. Модули (простые числа): 2. Максимальная относительная погрешность: Максимальная абсолютная погрешность Правило выбора модулей: где длина целой части длина дробной части

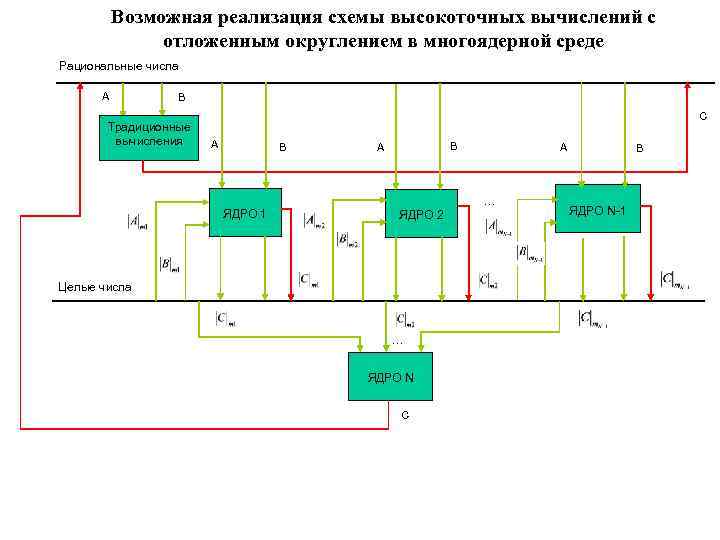Возможная реализация схемы высокоточных вычислений с отложенным округлением в многоядерной среде Рациональные числа A B Традиционные вычисления C A B B A A … ЯДРО 1 ЯДРО 2 Целые числа … ЯДРО N C B ЯДРО N-1

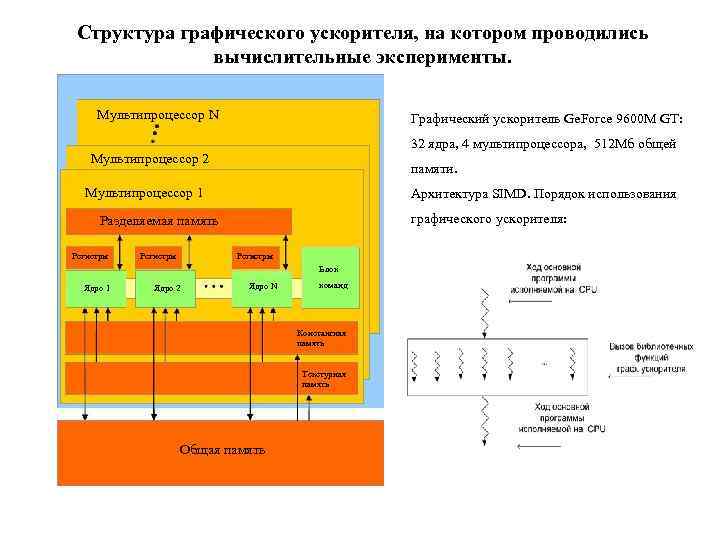Структура графического ускорителя, на котором проводились вычислительные эксперименты. Мультипроцессор N Графический ускоритель Ge. Force 9600 M GT: 32 ядра, 4 мультипроцессора, 512 Мб общей Мультипроцессор 2 памяти. Мультипроцессор 1 Архитектура SIMD. Порядок использования графического ускорителя: Разделяемая память Регистры Блок Ядро 1 Ядро 2 Ядро N команд Константная память Текстурная память Общая память

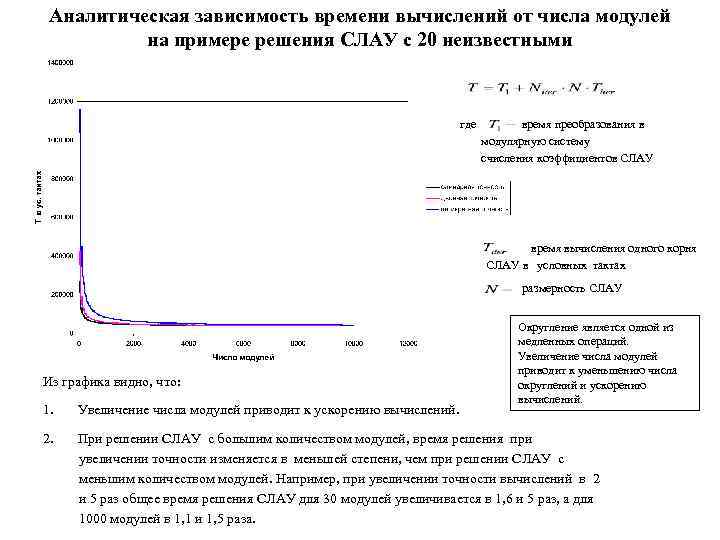Аналитическая зависимость времени вычислений от числа модулей на примере решения СЛАУ с 20 неизвестными где время преобразования в модулярную систему счисления коэффициентов СЛАУ время вычисления одного корня СЛАУ в условных тактах размерность СЛАУ Из графика видно, что: Округление является одной из медленных операций. Увеличение числа модулей приводит к уменьшению числа округлений и ускорению вычислений. 1. Увеличение числа модулей приводит к ускорению вычислений. 2. При решении СЛАУ с большим количеством модулей, время решения при увеличении точности изменяется в меньшей степени, чем при решении СЛАУ с меньшим количеством модулей. Например, при увеличении точности вычислений в 2 и 5 раз общее время решения СЛАУ для 30 модулей увеличивается в 1, 6 и 5 раз, а для 1000 модулей в 1, 1 и 1, 5 раза.

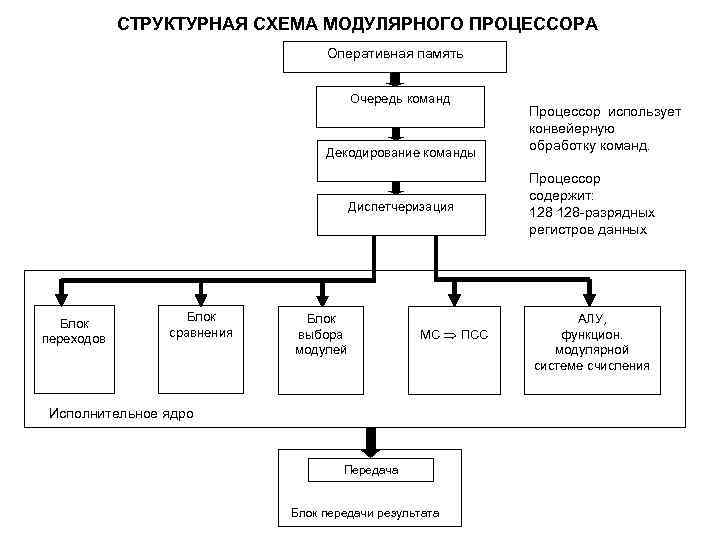СТРУКТУРНАЯ СХЕМА МОДУЛЯРНОГО ПРОЦЕССОРА Оперативная память Очередь команд Декодирование команды Диспетчеризация Блок переходов Блок сравнения Блок выбора модулей МС ПСС Исполнительное ядро Передача Блок передачи результата Процессор использует конвейерную обработку команд. Процессор содержит: 128 -разрядных регистров данных АЛУ, функцион. модулярной системе счисления

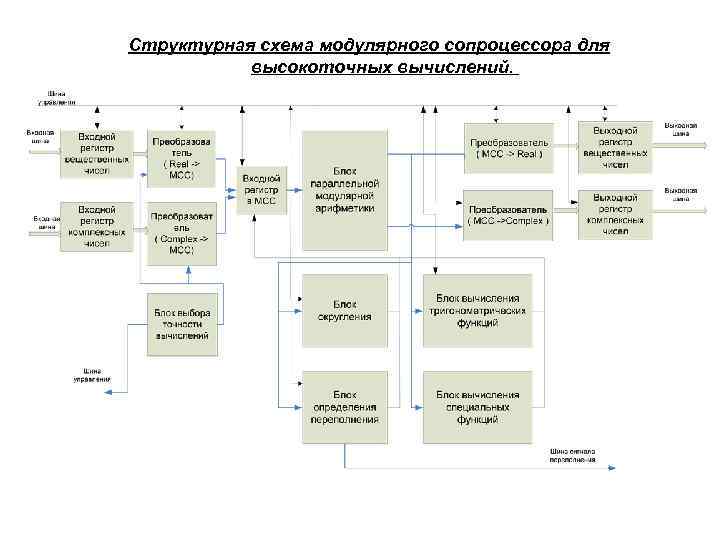Структурная схема модулярного сопроцессора для высокоточных вычислений.

Целесообразность создания сопроцессора ориентированного на вычисления повышенной точности на основе модулярной арифметики. 1. Сложность неограниченного повышения точности вычислений без существенного снижения быстродействия в рамках арифметики с плавающей точкой. 2. Резкая потеря точности компьютерных вычислений как следствие проявления недостатков арифметики с плавающей точкой. 3. Возможность модулярной системы счисления для единообразного представления и обработки целых, дробных и и комплексных чисел. 4. Исключение резкой потери точности выполнения арифметических операций с величинами, сильно отличающимися друг от друга по величине в модулярной системе счисления. 5. Динамическое изменение точности вычислений в широком диапазоне по команде модулярного сопроцессора. 6. Непрерывно растущие требования к точности компьютерных вычислений при решении вычислительных задач большой размерности.

Характеристики модулярного сопроцессора 1. Возможность наращивания точности вычислений за счет использования дополнительных модулей. 2. Одно АЛУ для работы с целыми, дробными, комплексными числами. (В традиционном сопроцессоре отдельные блоки для плавающей и целочисленной арифметики) 3. Аппаратная поддержка третьей формы представления вещественных чисел типа RATIONAL. 4. Одинаковая точность машинного представления всех чисел лежащих внутри допустимого диапазона. (В традиционной арифметике неодинаковая точность машинного представления чисел из-за неравномерного распределения чисел с плавающей точкой) 5. Мультиконвейерная архитектура модулярного сопроцессора.

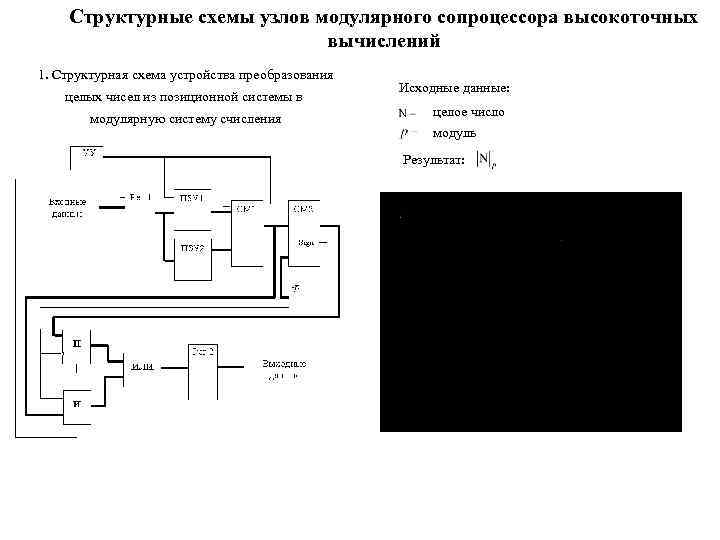Структурные схемы узлов модулярного сопроцессора высокоточных вычислений 1. Структурная схема устройства преобразования целых чисел из позиционной системы в модулярную систему счисления Исходные данные: целое число модуль Результат:

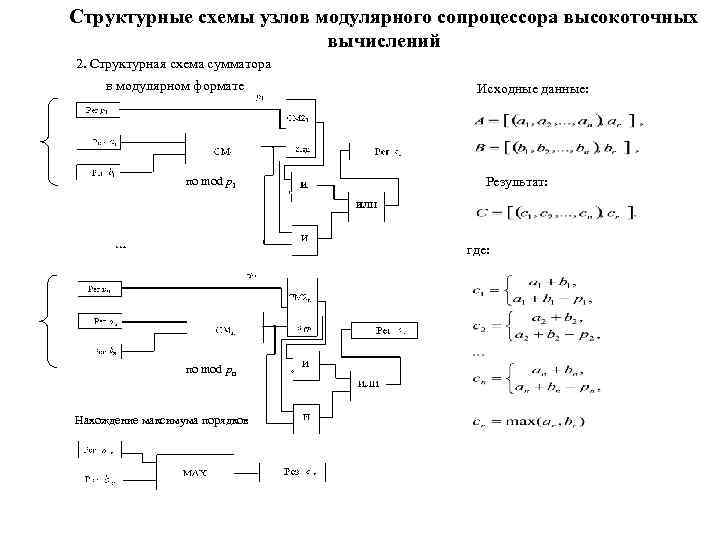Структурные схемы узлов модулярного сопроцессора высокоточных вычислений 2. Структурная схема сумматора в модулярном формате по mod p 1 Исходные данные: Результат: где: по mod pn Нахождение максимума порядков

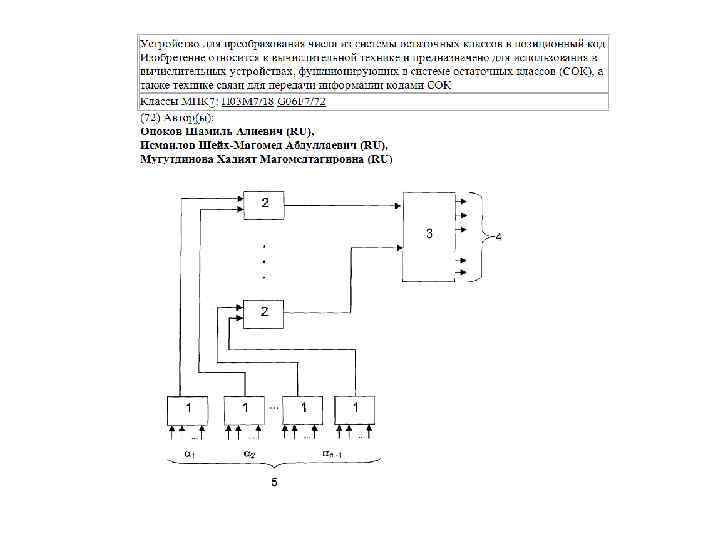
Сводная таблица структурных схем с оценкой временных затрат