Морфологическое описание систем Изучение особенностей информации, содержащейся в

Морфологическое описание систем Изучение особенностей информации, содержащейся в структуре системы, является предметом морфологического (структурного) анализа систем.

Целями структурного анализа являются: - разработка правил символического отображения систем; - оценка качества структуры системы; - изучение структурных свойств системы в целом и ее подсистем; -выработка заключения об оптимальности структуры системы и рекомендаций по дальнейшему ее совершенствованию.

В структурном подходе выделяются два этапа: • определение состава системы; • выяснение связей между ними.

Определение элементного состава • гомогенный (однотипные элементы) – гомогенности, как правило, сопутствует избыточность и наличие скрытых (потенциальных) возможностей; • гетерогенные элементы специализированы, они экономичны и могут быть эффективными в узком диапазоне внешних условий.

Структурные свойства систем Определяются характером и устойчивостью отношений между элементами. По характеру отношений между элементами структуры делятся на: • многосвязные; • иерархические; • смешанные.

Теоретико-множественное морфологическое описание SM={S, V, δ, K} S={Si} – множество элементов и их свойств V={Vj} – множество связей δ- структура К – композиция Все множества конечны

Будем различать в S: Состав: гомогенный гетерогенный смешанный неопределенный Свойства элементов: информационные энергетические информационно-энергетические вещественно-энергетические неопределенные

Будем различать во множестве V: Назначение связей: информационные вещественные энергетические Характер связей: прямые обратные нейтральные

Будем различать в δ: Устойчивость структуры: детерминированная вероятностная хаотическая Построения: иерархические многосвязные смешанные преобразующиеся

Будем различать в множестве К: Композиции: слабые с эффекторными подсистемами с рецепторными подсистемами с рефлексивными подсистемами полные неопределенные

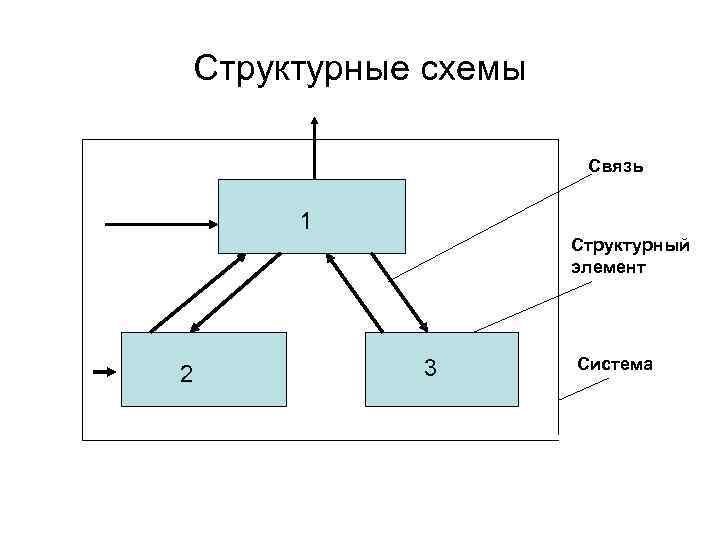
Структурные схемы Связь 1 Структурный элемент 2 3 Система

Графы G=(M, R, P) M – множество вершин, R – множество ребер (или дуг графа), Р – предикат инцидентности вершин и ребер графа P(x, y, r)=1 означает, что вершины x, y€М инцидентны (связаны) ребру графа r€R Граф называется ориентированным, если расположение смежных вершин имеет значение. Неориентированный граф не содержит ориентированных ребер.

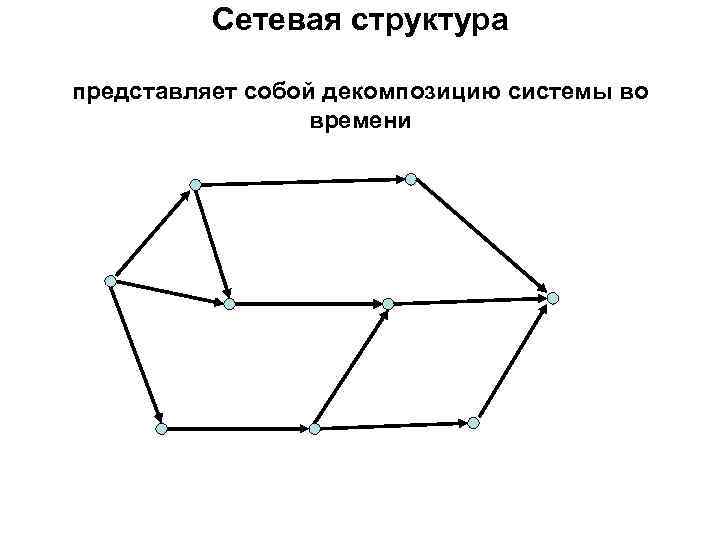
Сетевая структура представляет собой декомпозицию системы во времени

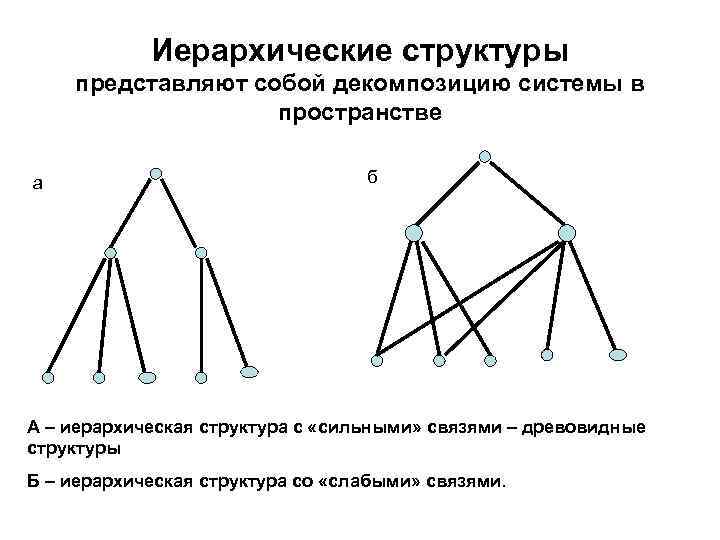
Иерархические структуры представляют собой декомпозицию системы в пространстве а б А – иерархическая структура с «сильными» связями – древовидные структуры Б – иерархическая структура со «слабыми» связями.

Многоуровневые иерархические структуры Общие характеристики всех иерархических систем: • последовательное вертикальное расположение подсистем; • приоритет действия или право вмешательства подсистем верхнего уровня; • зависимость действий подсистем верхнего уровня от фактического исполнения нижними уровнями своих функций. Три понятия уровней: - Уровень описания, или уровень абстрагирования страты. - Уровень сложности принимаемого решения – слои. - Организационный уровень – эшелоны.

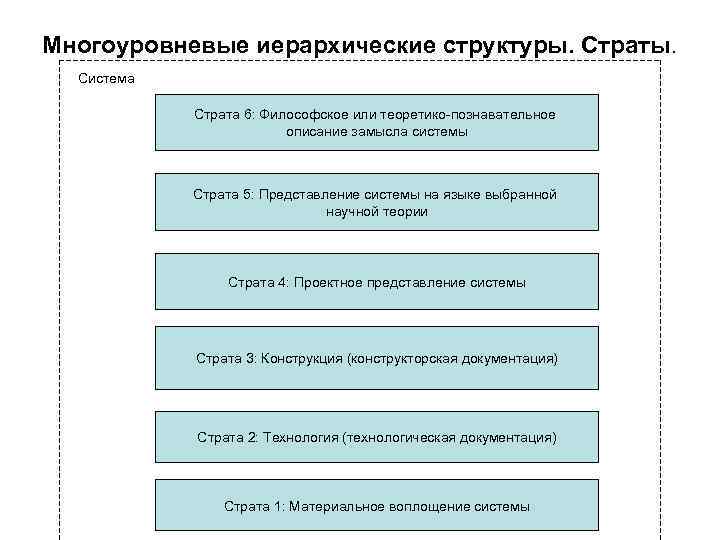
Многоуровневые иерархические структуры. Страты. Система Страта 6: Философское или теоретико-познавательное описание замысла системы Страта 5: Представление системы на языке выбранной научной теории Страта 4: Проектное представление системы Страта 3: Конструкция (конструкторская документация) Страта 2: Технология (технологическая документация) Страта 1: Материальное воплощение системы

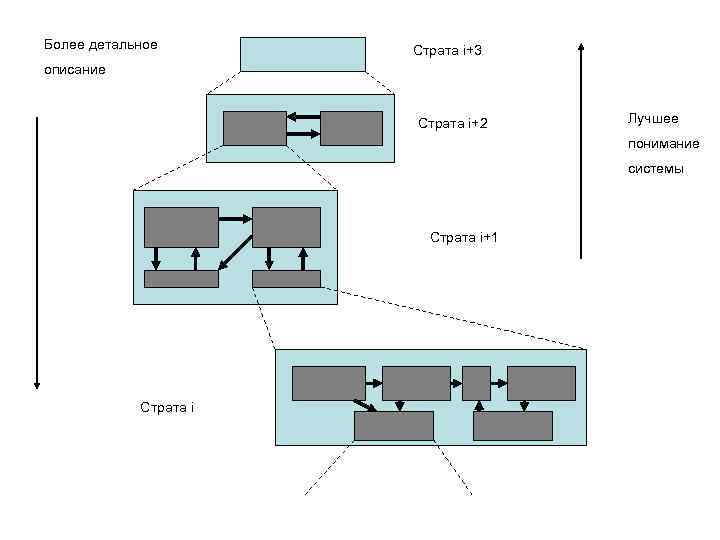
Более детальное Страта i+3 описание Страта i+2 Лучшее понимание системы Страта i+1 Страта i

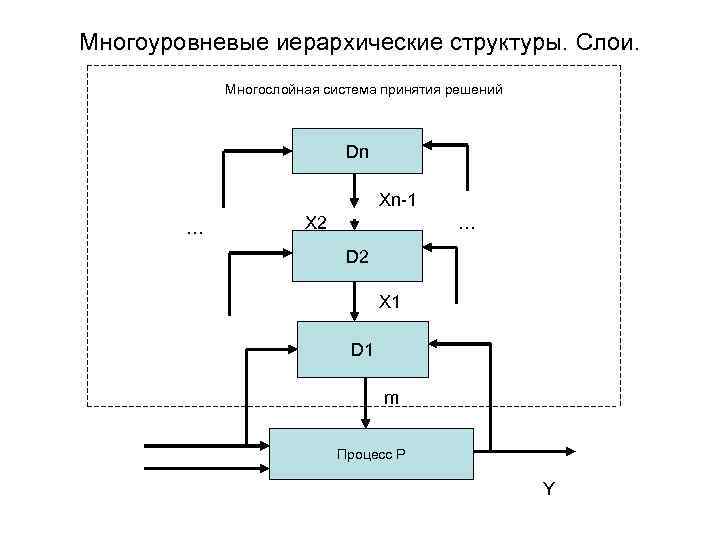
Многоуровневые иерархические структуры. Слои. Многослойная система принятия решений Dn Xn-1 … X 2 … D 2 X 1 D 1 m Процесс Р Y

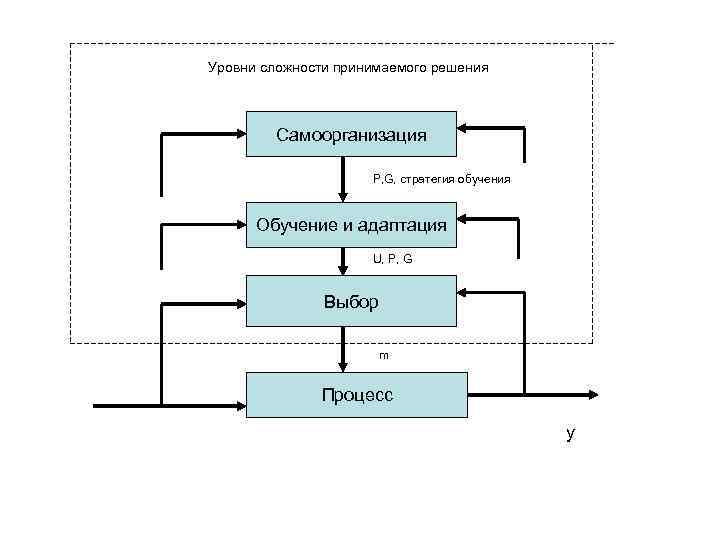
Уровни сложности принимаемого решения Самоорганизация P, G, стратегия обучения Обучение и адаптация U, P, G Выбор m Процесс y

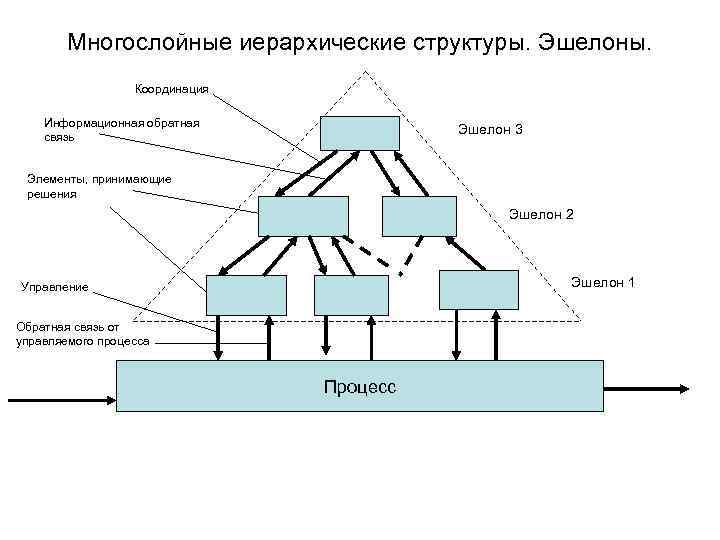
Многослойные иерархические структуры. Эшелоны. Координация Информационная обратная связь Эшелон 3 Элементы, принимающие решения Эшелон 2 Эшелон 1 Управление Обратная связь от управляемого процесса Процесс

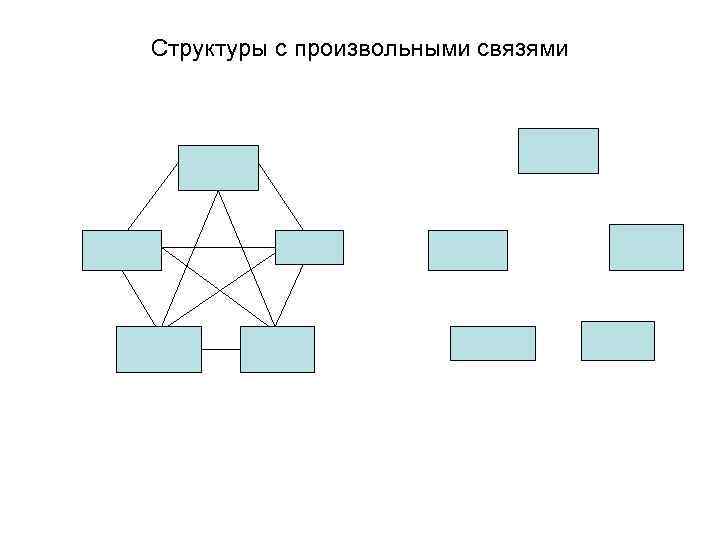
Структуры с произвольными связями

Системная сложность. Предел Бремермана. N=E/ΔE, Е – энергия которой мы располагаем, ΔE – энергетический уровень Принцип Гейзенберга ΔE·Δt>h, где Δt – длительность интервала наблюдения, h=6. 25 10**27 эрг/c – постоянная Планка. N>E Δt/h E=mc**2 (c=3 10**10 см/c) N=mc**2 Δt/h Измеритель массы 1 г за время 1 с может обработать не более N=1, 36 10**47 бит Измеритель массы Земли m=6 10**27 г за время существования Земли 10**19 с смог бы обработать 10**93 бит

Мера сложности системы Различаются две модификации сложности: - аддитивная сложность (сложность целого сводится к сумме свойств составных элементов); - неаддитивная сложность.

Два основных принципа оценки сложности • Первый – оценка объема информации, необходимой для описание системы объекта. • Второй – оценка объема информации, необходимой для разрешения нечеткости (неопределенности) системы.

Дескриптивная сложность (аддитивная) сводится к оценке числа элементов системы, их состояний и отношений между ними. ДМС обеспечивает потребности решения задач, объектом которых являются детерминированные системы. В классе недетерминированных систем ДМС неприемлема, так как она не позволяет учесть сложность, которую вносит нечеткость стохастической системы.

Оценка сложности вероятностных систем на основе статистической меры количества информации (К. Шеннон) Пример 1. Пусть система S содержит N переменных, каждая переменная имеет K состояний. Пусть все состояния равновероятны. У такой системы мощность полного множества состояний равна |C|=K**N, вероятностная функция ограничений имеет вид P={P 1=Pj=1/K**N}. В этом случае энтропия будет равна H=N log. K H(x)=-Σp(i)log 2{1/p(i)}