Monte Carlo Methods Mark A Novotny Random topics

Monte Carlo Methods Mark A. Novotny Random topics about random things for random people Dept. of Physics and Astronomy Mississippi State U. man 40@ra. msstate. edu Supported in part by NSF DMR 0120310 and ITR/AP(MPS)0113049 NIHES EERC Oct. 25, 2002

Where is Monte Carlo? • Europe • Principality of Monaco • Monte Carlo is 1 of 5 regions of Monaco • Monte Carlo founded in 1866 by Prince Charles III • Renowned casino, luxurious hotels, beaches, … NIHES EERC Oct. 25, 2002

What is a Monte Carlo simulation? • In a Monte Carlo simulation we attempt to follow the `time dependence’ of a model for which change, or growth, does not proceed in some rigorously predefined fashion (e. g. according to Newton’s equations of motion) but rather in a stochastic manner which depends on a sequence of random numbers which is generated during the simulation. • Landau and Binder, A Guide to Monte Carlo Simulations in Statistical Physics (Cambridge U. Press, Cambridge U. K. , 2000), p. 1. NIHES EERC Oct. 25, 2002

Birth of the Monte Carlo method • Los Alamos National Laboratory • 1953 Physical Review • Metropolis, Rosenbluth, Teller, and Teller • Conferences/Monte. Carlo. Methods/ “The only good Monte Carlo is a dead Monte Carlo. ” NIHES EERC Oct. 25, 2002 Trotter and Turkey, 1954

OUTLINE • Random numbers • Integrals via Monte Carlo • Importance Sampling Monte Carlo • Dynamic Monte Carlo • Decay of nuclei (birthdeath processes) NIHES EERC Oct. 25, 2002 • Random motion in 1 dimension • Long-time simulations (Monte Carlo with Absorbing Markov Chains, MCAMC) • Parallel dynamic Monte Carlo simulations

(not-really, but almost) • • Random Numbers Uniformly distributed numbers in [0, 1] How good is `good enough’? `religious question’ Linear congruential, R 250, Marsaglia, 4 -tap, R 250 4 -tap system supplied • Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin. • John von Neumann (1951) NIHES EERC Oct. 25, 2002

(not-really, but almost) • • Random Numbers from R 250 Xn = XOR( Xn-p , Xn-q ) XOR(, ) is exclusive OR operator With p 2+q 2+1=prime (p and q are Mersine primes) R 98: p=98, q=27 R 250: p=250, q=103 R 1279: p=1279, q=216 or 418 R 9689: p=9689, q=84, 471, 1836, 2444, or 4187 NIHES EERC Oct. 25, 2002

OUTLINE • Random numbers • Integrals via Monte Carlo • Importance Sampling Monte Carlo • Dynamic Monte Carlo • Decay of nuclei (birthdeath processes) NIHES EERC Oct. 25, 2002 • Random motion in 1 dimension • Long-time simulations (Monte Carlo with Absorbing Markov Chains, MCAMC) • Parallel dynamic Monte Carlo simulations

Calculate p=pi using Monte Carlo • Set Nin=0 • Do N times o o o Calculate 3 random numbers, r 1, r 2, r 3 Let x=r 1 Let y=r 2 Use r 3 to choose quadrant (change signs of x and y) If x 2+y 2. le. 1 set Nin=Nin+1 • Estimate for p=pi = 4 Nin / N NIHES EERC Oct. 25, 2002

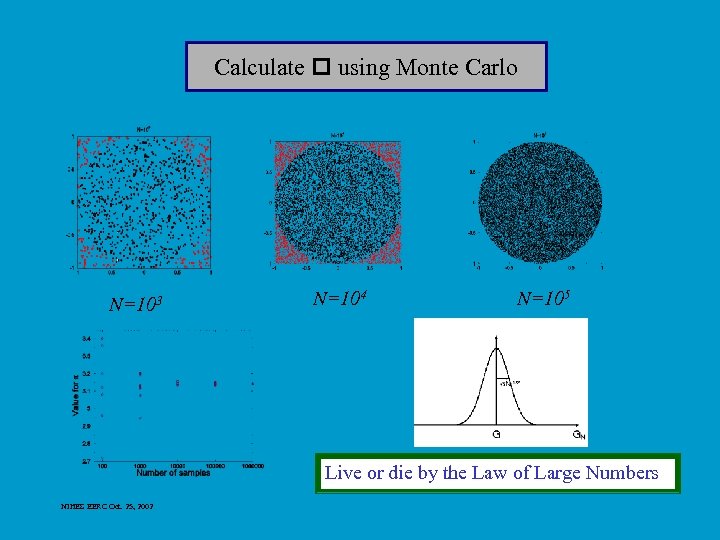Calculate p using Monte Carlo N=103 N=104 N=105 Live or die by the Law of Large Numbers NIHES EERC Oct. 25, 2002

OUTLINE • Random numbers • Integrals via Monte Carlo • Importance Sampling Monte Carlo • Dynamic Monte Carlo • Decay of nuclei (birthdeath processes) NIHES EERC Oct. 25, 2002 • Random motion in 1 dimension • Long-time simulations (Monte Carlo with Absorbing Markov Chains, MCAMC) • Parallel dynamic Monte Carlo simulations

Importance Sampling Monte Carlo • Old way: choose points with equal probability from rectangle with a

OUTLINE • Random numbers • Integrals via Monte Carlo • Importance Sampling Monte Carlo • Dynamic Monte Carlo • Decay of nuclei (birthdeath processes) NIHES EERC Oct. 25, 2002 • Random motion in 1 dimension • Long-time simulations (Monte Carlo with Absorbing Markov Chains, MCAMC) • Parallel dynamic Monte Carlo simulations

Dynamic Monte Carlo • For Static Monte Carlo the order of generation of points does not matter (like finding the integrals) • For Dynamic Monte Carlo the order does matter • This gives a Markov chain method, governed by the Master Equation NIHES EERC Oct. 25, 2002

OUTLINE • Random numbers • Integrals via Monte Carlo • Importance Sampling Monte Carlo • Dynamic Monte Carlo • Decay of nuclei (birthdeath processes) NIHES EERC Oct. 25, 2002 • Random motion in 1 dimension • Long-time simulations (Monte Carlo with Absorbing Markov Chains, MCAMC) • Parallel dynamic Monte Carlo simulations

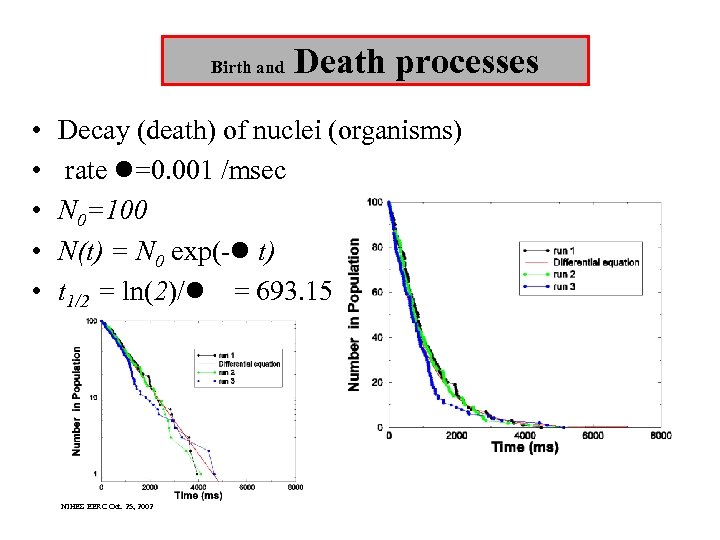Birth and • • • Death processes Decay (death) of nuclei (organisms) rate l=0. 001 /msec N 0=100 N(t) = N 0 exp(-l t) t 1/2 = ln(2)/l = 693. 15 NIHES EERC Oct. 25, 2002

Birth and • • Death processes Start with N=N 0 individuals Start time t=0 Assume that decay (death) constant l<1 For each nucleus which has not yet decayed u. Generate a random number 0

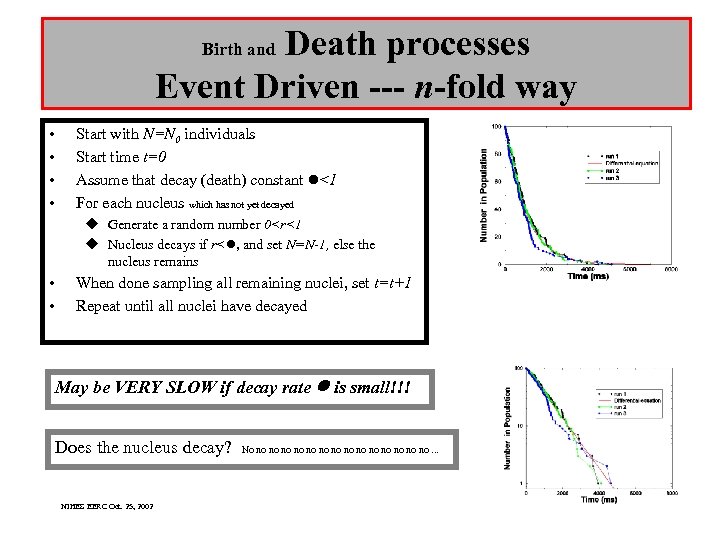Death processes Event Driven --- n-fold way Birth and • • Start with N=N 0 individuals Start time t=0 Assume that decay (death) constant l<1 For each nucleus which has not yet decayed u Generate a random number 0

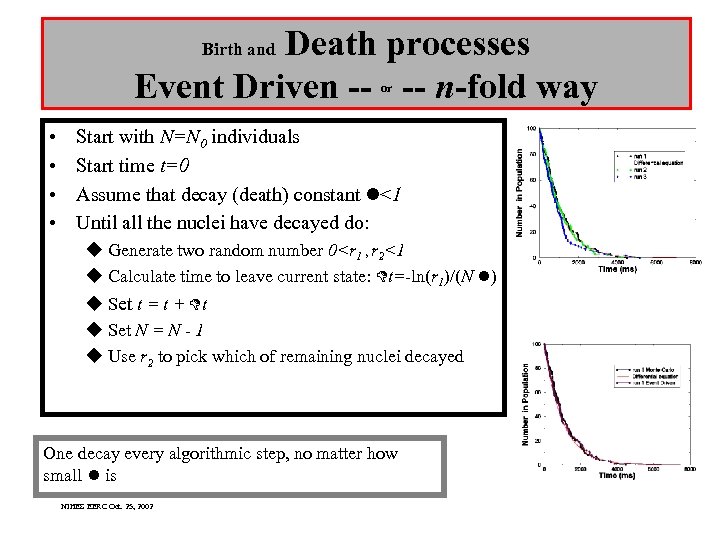Death processes Event Driven -- -- n-fold way Birth and or • • Start with N=N 0 individuals Start time t=0 Assume that decay (death) constant l<1 Until all the nuclei have decayed do: u Generate two random number 0

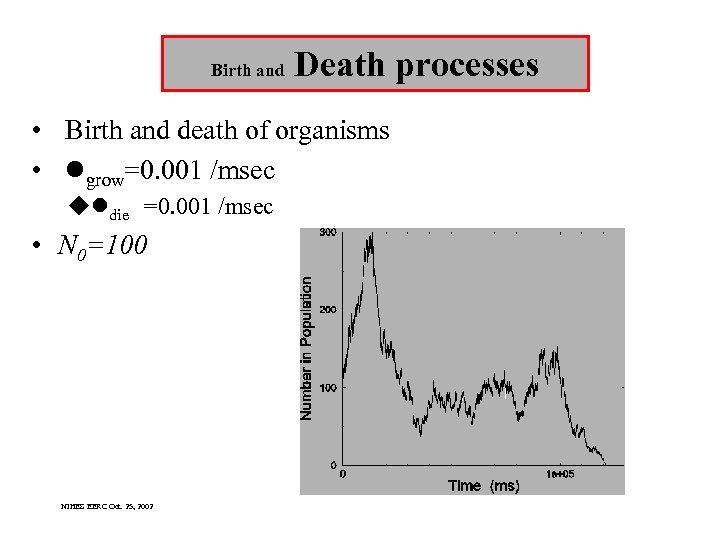Birth and Death processes • Birth and death of organisms • lgrow=0. 001 /msec uldie =0. 001 /msec • N 0=100 NIHES EERC Oct. 25, 2002

OUTLINE • Random numbers • Integrals via Monte Carlo • Importance Sampling Monte Carlo • Dynamic Monte Carlo • Decay of nuclei (birthdeath processes) NIHES EERC Oct. 25, 2002 • Random motion in 1 dimension • Long-time simulations (Monte Carlo with Absorbing Markov Chains, MCAMC) • Parallel dynamic Monte Carlo simulations

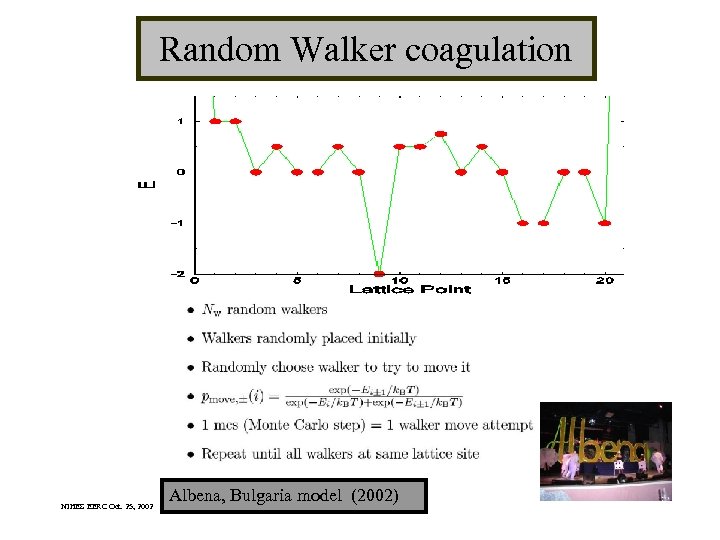Random Walker coagulation NIHES EERC Oct. 25, 2002 Albena, Bulgaria model (2002)

Random Walker coagulation Albena, Bulgaria model (2002) NIHES EERC Oct. 25, 2002

Random Walker coagulation NIHES EERC Oct. 25, 2002

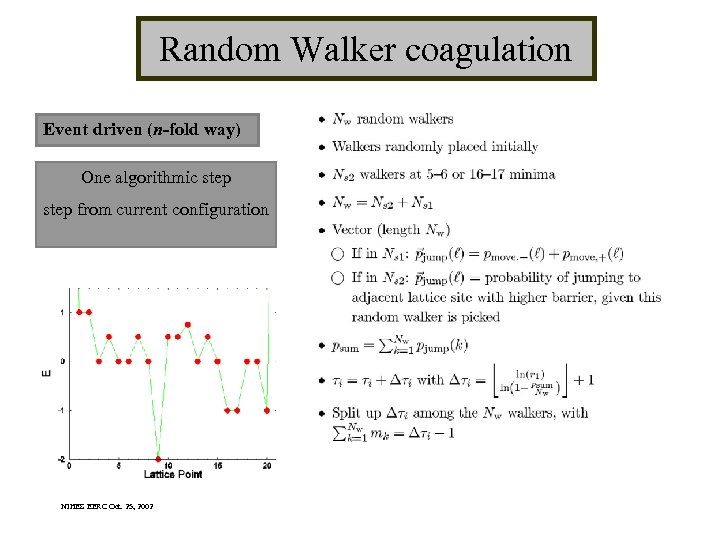Random Walker coagulation Event driven (n-fold way) One algorithmic step from current configuration NIHES EERC Oct. 25, 2002

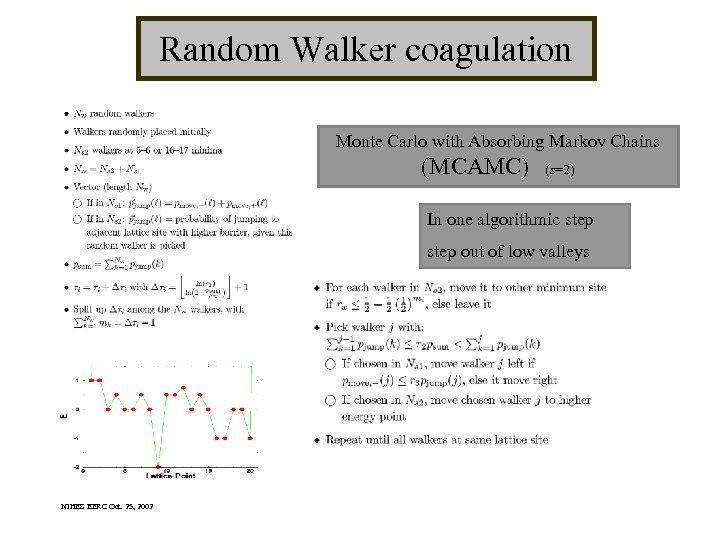Random Walker coagulation Monte Carlo with Absorbing Markov Chains (MCAMC) (s=2) In one algorithmic step out of low valleys NIHES EERC Oct. 25, 2002

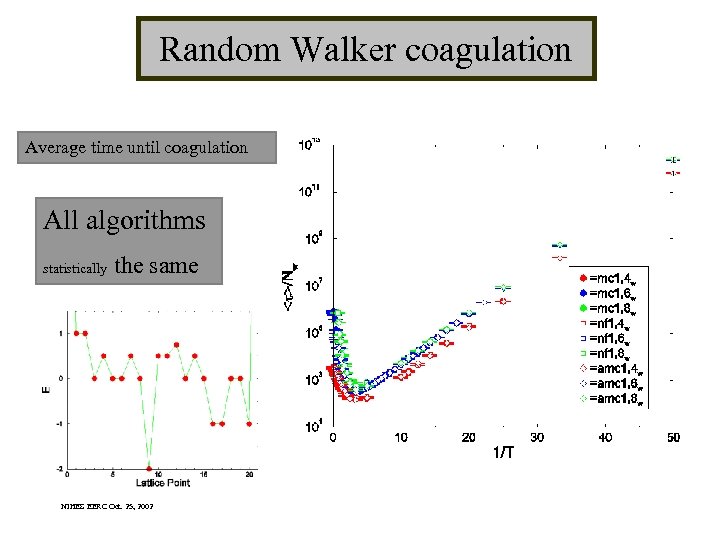Random Walker coagulation Average time until coagulation All algorithms statistically the same NIHES EERC Oct. 25, 2002

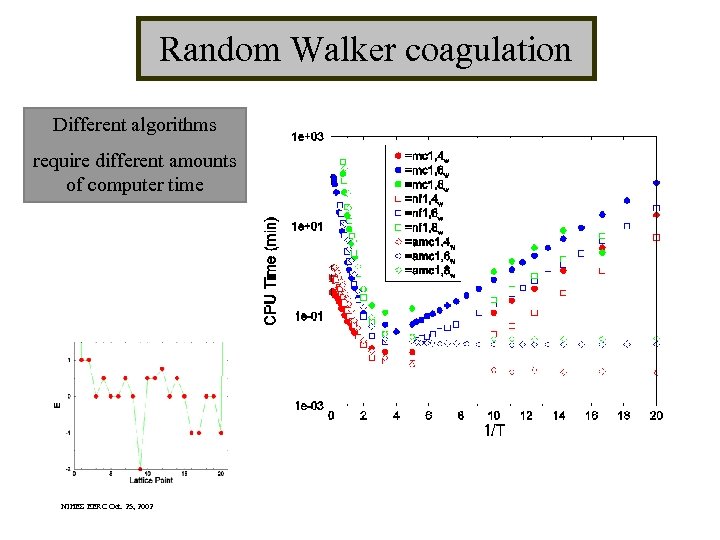Random Walker coagulation Different algorithms require different amounts of computer time NIHES EERC Oct. 25, 2002

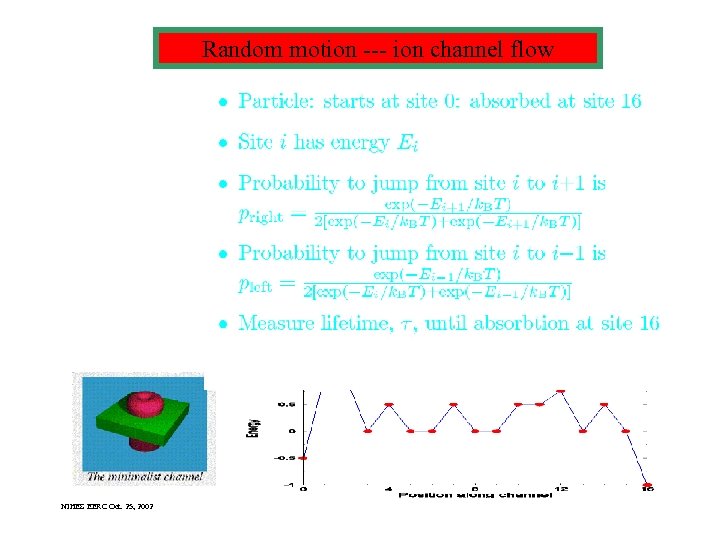
Random motion --- ion channel flow Random motion (of a random walker) through a channel NIHES EERC Oct. 25, 2002

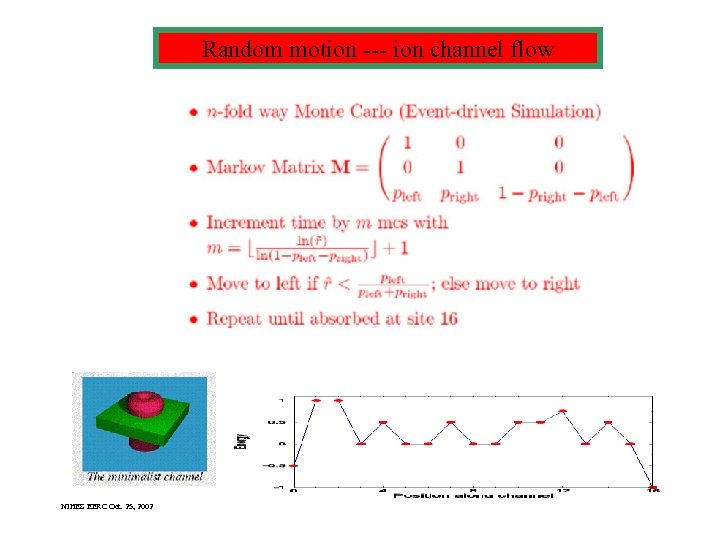
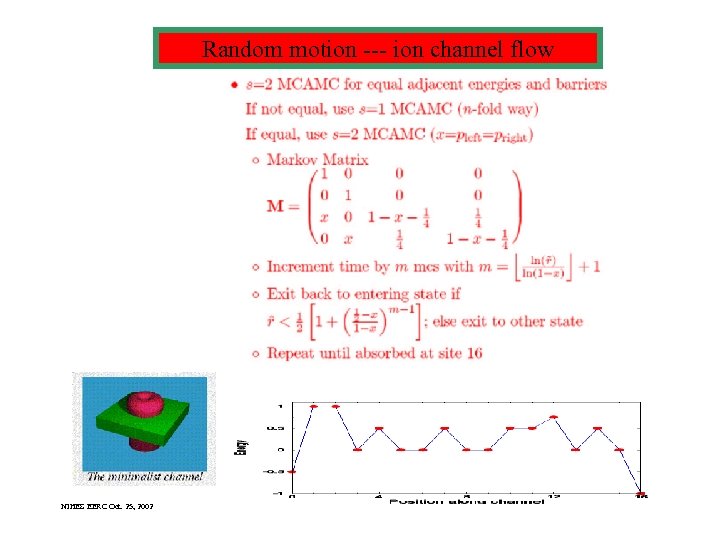Random motion --- ion channel flow NIHES EERC Oct. 25, 2002

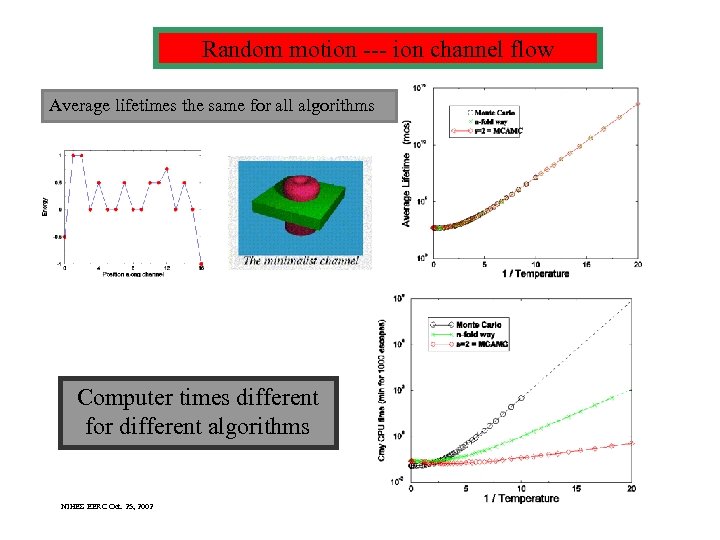Random motion --- ion channel flow Average lifetimes the same for all algorithms Computer times different for different algorithms NIHES EERC Oct. 25, 2002

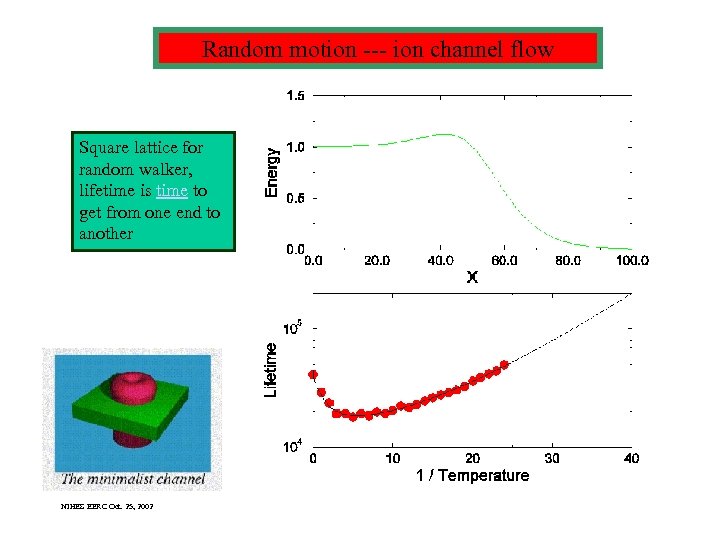Random motion --- ion channel flow Square lattice for random walker, lifetime is time to get from one end to another NIHES EERC Oct. 25, 2002

OUTLINE • Random numbers • Integrals via Monte Carlo • Importance Sampling Monte Carlo • Dynamic Monte Carlo • Decay of nuclei (birthdeath processes) NIHES EERC Oct. 25, 2002 • Random motion in 1 dimension • Long-time simulations (Monte Carlo with Absorbing Markov Chains, MCAMC) • Parallel dynamic Monte Carlo simulations

Monte Carlo for Ising models NIHES EERC Oct. 25, 2002

Monte Carlo for Ising models Use spin classes for Ising model --- square lattice has 10 spin classes • Every spin belongs to one of 10 classes • Probability of flipping a spin in each class is the same • If chosen, probability of flipping spin in class i is p(i) • Number of spins in class i is ci NIHES EERC Oct. 25, 2002

Monte Carlo for Ising models A GAME NIHES EERC Oct. 25, 2002

Monte Carlo for Ising models MCAMC n-fold way NIHES EERC Oct. 25, 2002

Monte Carlo for Ising models n-fold way with needed Bookkeeping NIHES EERC Oct. 25, 2002

Monte Carlo for Ising models MCAMC NIHES EERC Oct. 25, 2002

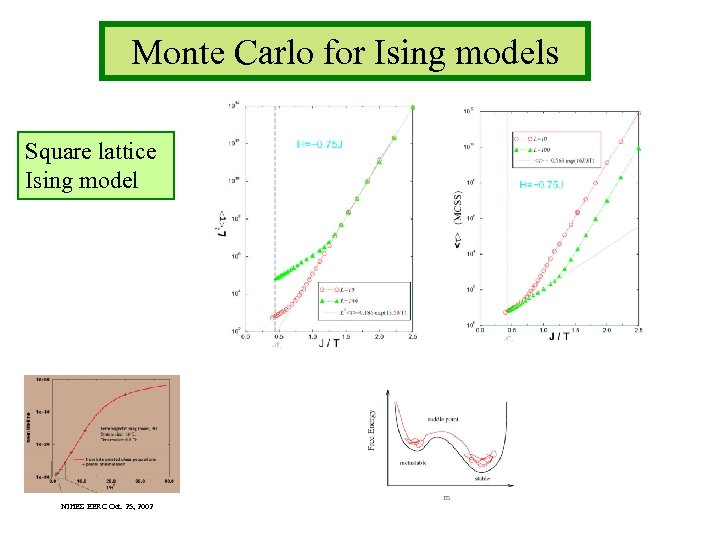Monte Carlo for Ising models Square lattice Ising model NIHES EERC Oct. 25, 2002

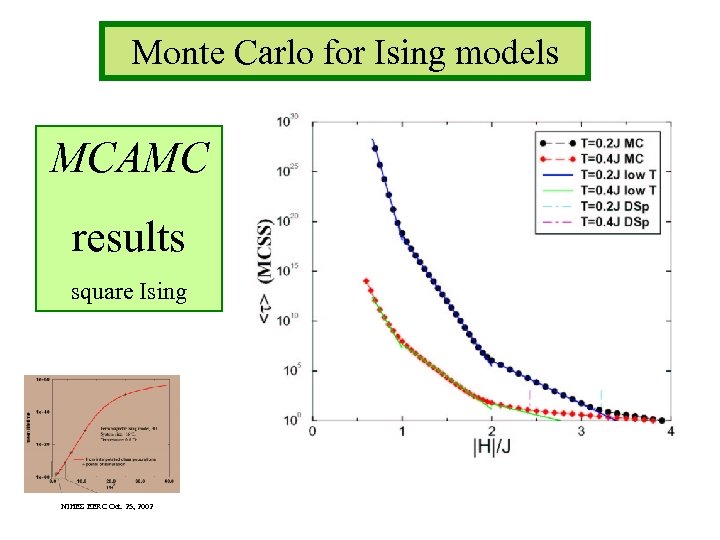Monte Carlo for Ising models MCAMC results square Ising NIHES EERC Oct. 25, 2002

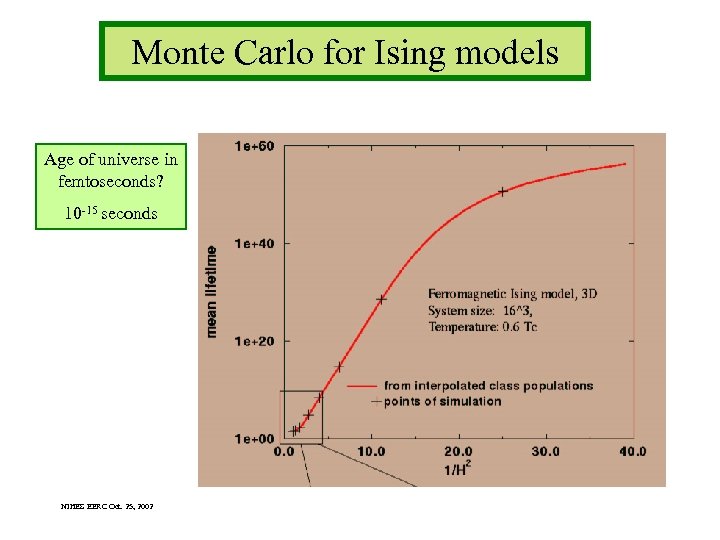Monte Carlo for Ising models Age of universe in femtoseconds? 10 -15 seconds NIHES EERC Oct. 25, 2002

OUTLINE • Random numbers • Integrals via Monte Carlo • Importance Sampling Monte Carlo • Dynamic Monte Carlo • Decay of nuclei (birthdeath processes) NIHES EERC Oct. 25, 2002 • Random motion in 1 dimension • Long-time simulations (Monte Carlo with Absorbing Markov Chains, MCAMC) • Parallel dynamic Monte Carlo simulations

Dynamic Monte Carlo Parallel Discrete Event Simulations • Dynamics for Materials • Dynamics for biological and ecological models • Dynamics of Magnets • Cell-phone switching • Spread of infectious diseases • Resource allocation following terrorist attacks • War-game scenarios NIHES EERC Oct. 25, 2002

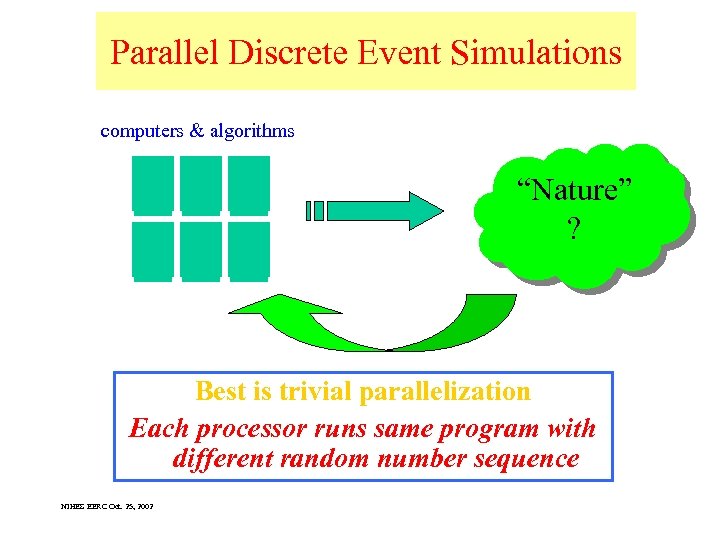Parallel Discrete Event Simulations computers & algorithms “Nature” ? Best is trivial parallelization Each processor runs same program with different random number sequence NIHES EERC Oct. 25, 2002

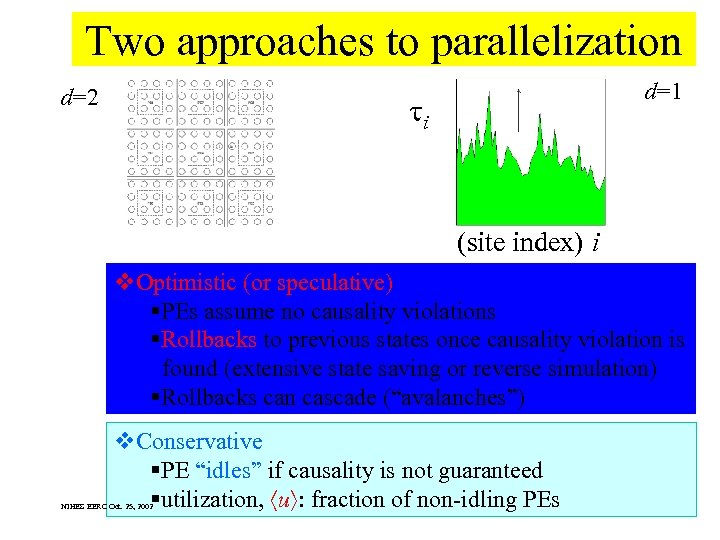Two approaches to parallelization d=2 d=1 i (site index) i v. Optimistic (or speculative) §PEs assume no causality violations §Rollbacks to previous states once causality violation is found (extensive state saving or reverse simulation) §Rollbacks can cascade (“avalanches”) v. Conservative §PE “idles” if causality is not guaranteed §utilization, u : fraction of non-idling PEs NIHES EERC Oct. 25, 2002

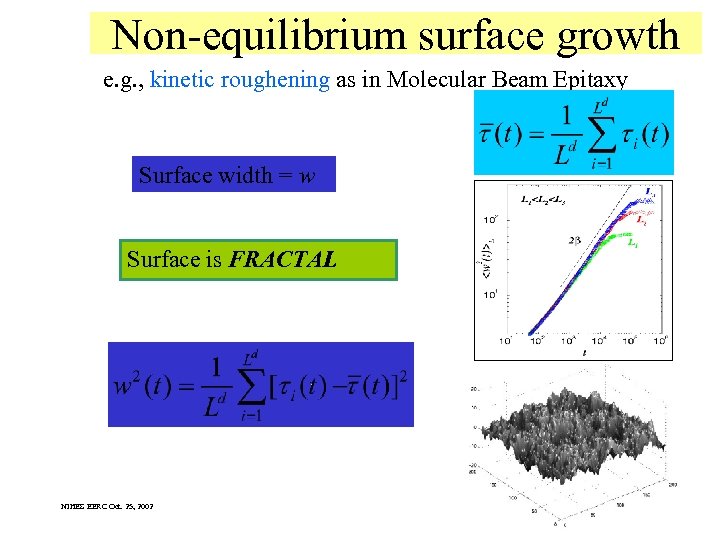Non-equilibrium surface growth e. g. , kinetic roughening as in Molecular Beam Epitaxy Surface width = w Surface is FRACTAL NIHES EERC Oct. 25, 2002

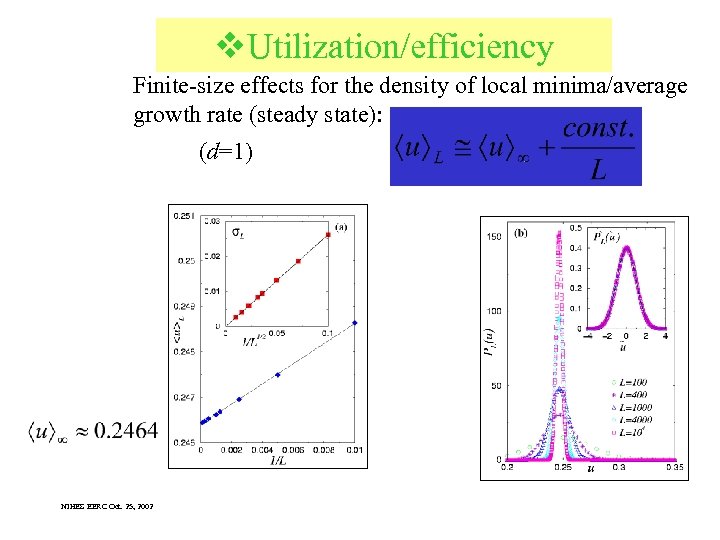v. Utilization/efficiency Finite-size effects for the density of local minima/average growth rate (steady state): (d=1) NIHES EERC Oct. 25, 2002

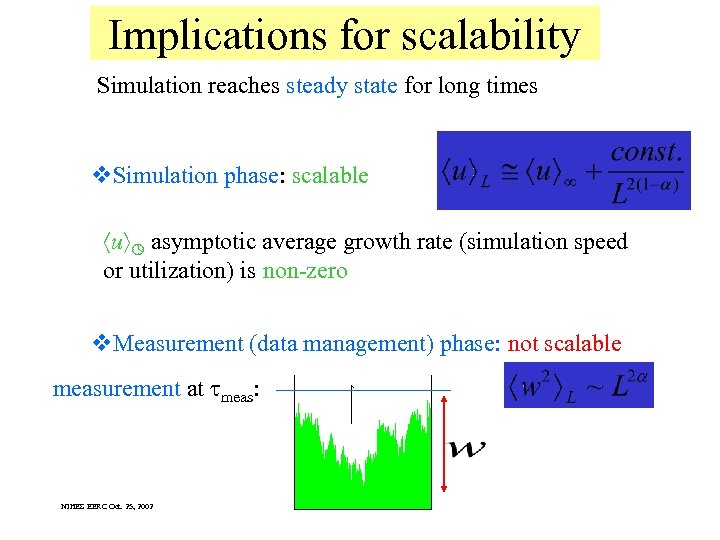Implications for scalability Simulation reaches steady state for long times v. Simulation phase: scalable u asymptotic average growth rate (simulation speed or utilization) is non-zero v. Measurement (data management) phase: not scalable measurement at meas: NIHES EERC Oct. 25, 2002

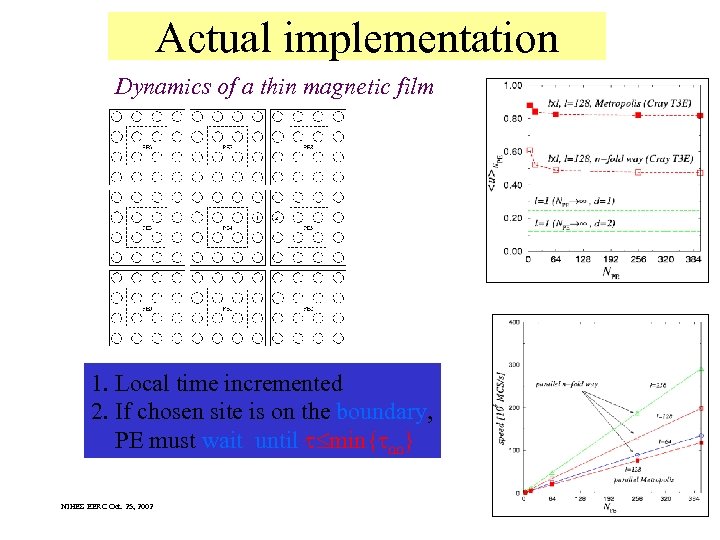Actual implementation Dynamics of a thin magnetic film 1. Local time incremented 2. If chosen site is on the boundary, PE must wait until min{ nn} NIHES EERC Oct. 25, 2002

The Physics of Queuing • PDES applicable to many situations • Can be made scalable (patent applied for) • Use ideas from physics to understand & improve computer science & biological applications NIHES EERC Oct. 25, 2002

References and Links Novotny and coworkers • For a review of advanced dynamic methods see: M. A. Novotny in Annual Reviews of Computational Physics IX, ed. D. Stauffer, (World Scientific, Singapore, 2001), p. 153; preprint xxx. lanl. gov/condmat/0109182 click---HERE. • Metastability: Physical Review Letters, 81, 834 (1998). • Monte Carlo with Absorbing Markov Chains: Physical Review Letters, 74, 1 (1995); erratum 75, 1424 (1995). • Discrete-time n-fold way: Computers in Physics, 9, 46 (1995). • Parallel Discrete Event Simulations, General: Physical Review Letters, 84, 1351 (2000). • Implementation of non-trivial parallel Monte Carlo: Journal of Computational Physics, 153, 488 (1999). • Projective Dynamics: Physical Review Letters, 80, 3384 (1998). • Constrained Transfer Matrix for metastability: Physical Review Letters, 71, 3898 (1993). NIHES EERC Oct. 25, 2002