Монотонности функции Функция f x называется возрастающей на

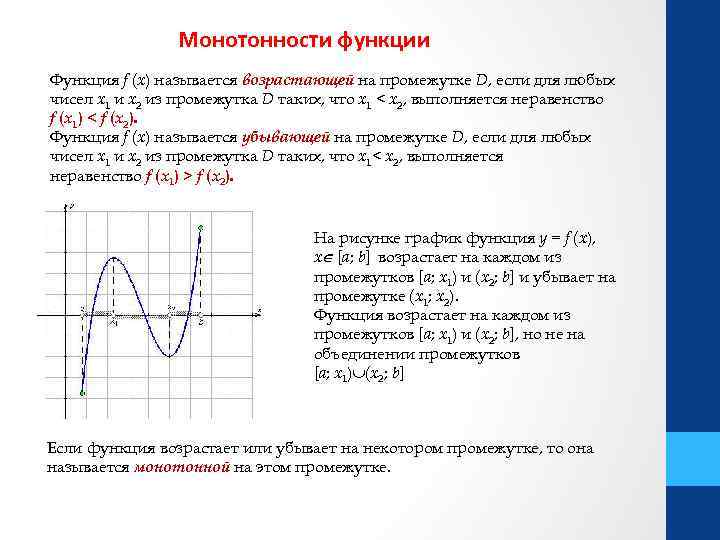Монотонности функции Функция f (x) называется возрастающей на промежутке D, если для любых чисел x 1 и x 2 из промежутка D таких, что x 1 < x 2, выполняется неравенство f (x 1) < f (x 2). Функция f (x) называется убывающей на промежутке D, если для любых чисел x 1 и x 2 из промежутка D таких, что x 1< x 2, выполняется неравенство f (x 1) > f (x 2). На рисунке график функция y = f (x), x [a; b] возрастает на каждом из промежутков [a; x 1) и (x 2; b] и убывает на промежутке (x 1; x 2). Функция возрастает на каждом из промежутков [a; x 1) и (x 2; b], но не на объединении промежутков [a; x 1) (x 2; b] Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Критерий нестрогой монотонности функции Теорема Для того, чтобы функция y=f(x) была возрастающей на интервале (a, b), необходимо и достаточно, чтобы первая производная функции была неотрицательной всюду на данном интервале: f′(x)≥ 0∀x∈(a, b). Аналогичный критерий действует для случая функции, убывающей на интервале (a, b): f′(x)≤ 0∀x∈(a, b). Доказательство Необходимое условие. Рассмотрим произвольную точку x 0∈(a, b). Если функция y=f(x) возрастает на (a, b), то по определению можно записать, что: ∀x∈(a, b): x > x 0 ⇒ f(x) > f(x 0); ∀x∈(a, b): x < x 0 ⇒ f(x) < f(x 0). Видно, что в обоих случаях выполняется неравенство f(x)−f(x 0)x−x 0 ≥ 0, где x ≠ x 0. В пределе при x→x 0 левая часть неравенства равна производной функции в точке x 0, т. е. по свойству сохранения знака предела: limx → x 0 f(x) − f(x 0)x − x 0 = f′(x 0) ≥ 0. Это соотношение справедливо для любых x 0∈ (a, b).

Критерий нестрогой монотонности функции Рассмотрим достаточное условие, т. е. обратное утверждение. Доказательство Пусть производная f′(x) функции y = f(x) неотрицательна на интервале (a, b): f′(x 0)≥ 0∀x∈(a, b). Если x 1 и x 2 − две произвольные точки данного интервала, такие, что x 1< x 2, то можно записать: f(x 2)−f(x 1)=f′(c)(x 2−x 1), где c∈[x 1, x 2], ⇒c∈(a, b). Поскольку f′(c)≥ 0, то правая часть равенства неотрицательна. Следовательно, f(x 2)≥f(x 1). т. е. функция y=f(x) является возрастающей на интервале (a, b).

Для того, чтобы дифференцируемая на интервале (a, b) функция была строго возрастающей на этом интервале, необходимо и достаточно, чтобы выполнялись следующие условия: 1. f′(x)≥ 0∀x∈(a, b); 2. Производная f′(x) тождественно не равна нулю ни в каком промежутке [x 1, x 2]∈ (a, b). Достаточные условия строгой монотонности Если для всех x∈(a, b) выполняется условие f′(x)>0 всюду в интервале (a, b), кроме возможно лишь некоторых отдельных точек, в которых f′(x)=0, то функция f(x) является строго возрастающей. Соответственно, условие f′(x)<0 определяет строго убывающую функцию. Число точек, в которых f′(x)=0, является, как правило, конечным. Признак строгого возрастания (убывания) функции в точке: Теорема Пусть x 0∈(a, b). Если f′(x 0)>0, то функция f(x) строго возрастает в точке x 0; Если f′(x 0)<0, то функция f(x) строго убывает в точке x 0.

Необходимое условие экстремума Экстремумом функции называется максимальное (минимальное) значение функции на заданном множестве. Точка, в которой достигается экстремум называется точкой экстремума. Теорема. Пусть функция f определена и непрерывна в окрестности точки х0. Тогда, если х0 – точка максимума функции f, тоf'x 0 либо равна нулю, либо не существует. Замечание. Здесь имеется в виду, что не существует конечной производной, а бесконечная производная может существовать. Доказательство теоремы. Если f'(x 0) не существует, то теорема доказана. Если же f'(x 0) существует, в окрестности точки х0 функция удовлетворяет условиям теоремы Ферма. Согласно этой теореме f'(x 0)=0. Ч. т. д. ■ Определение. Точки, в которых выполняется необходимое условие экстремума (т. е. производная либо равна нулю, либо не существует), называются критическими точками функции. Определение. Точки, в которых производная равна нулю, называются стационарными точками функции. Замечание Все стационарные точки функции являются, конечно, и. критическими.

Достаточные условия экстремума в терминах первой производной Функция g(x) в точке х0 имеет экстремум (максимум или минимум), если функция определена в двухсторонней окрестности точки х0 и для всех точек x некоторой области: 0 х- х0 , выполнено соответственно неравенство g(x) g(x 0) (в случае максимума) или g(x) g(x 0) (в случае минимума). Экстремум функции находиться из условия: g (x 0)=0, если производная существует, т. е. приравниваем первую производную функции к нулю.

1) Первое достаточное условие: Если: а) f(x) непрерывная функция и определена в некоторой окрестности точки х0 такой, что первая производная в данной точке равна нулю или не существует. б) f(x) имеет конечную производную в окрестности задания и непрерывности функции в) производная сохраняет определенный знак справа от точки х0 и слева от этой же точки, тогда точку х0 можно охарактеризовать следующим образом Это условие не очень удобное, так как нужно проверять множество условий и запоминать таблицу, однако если ничего не сказано о производных высших порядках, то это единственный способ найти экстремум функции. 2) Второе достаточное условие Если функция g(x) обладает второй производной g (x) причем в некоторой точке x 0 первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка x 0 экстремум функции g(x), причем если g (x) 0, то точка является максимумом; если g (x) 0 , то точка является минимумом.

Достаточные условия экстремума в терминах первой производной Теорема Если непрерывная функция f(x) дифференцируема в некоторой окрестности критической точки xo и при переходе через нее (слева направо) производная f (x) меняет знак с «+» на «-» , то xo есть точка максимума с «-» на «+» - то xo есть точка минимума ; . Доказательство : Рассмотрим окрестность точки xo. Пусть f (x) 0 х (хо - ; хо) и f (x) 0 х (хо; хо + ; ). Тогда функция f(x) возрастает на интервале (хо - ; хо), а на интервале (хо; хо + ; ) она убывает. Отсюда следует, что значение f(x) в точке xo является наибольшим на интервале (хо - ; хо + ; ) , т. е. f(x) f(xо) для всех х (хо - ; хо) (хо; хо + ; ). Следовательно xo есть точка максимума.

Достаточные условия экстремума в терминах первой производной Теорема(первый достаточный признак экстремума). Если производная f '(x) функции f(x) обращается в нуль в точке xо или не существует и при переходе через xо меняет свой знак, то функция f(x) имеет в этой точке экстремум (максимум, если знак меняется с "+" на "-", и минимум, если знак меняется с "-" на "+"). Доказательство. Если производная f '(x) при переходе через x = xо меняет знак с "+" на "-", то это означает, что при достаточно малом h производная f '(x) положительна в интервале (xо h, xо ) и отрицательна в интервале (xо , xо + h). Следовательно, функция f(x) в интервале (xо - h, xо) возрастает, а в интервале (xо , xо+ h) убывает, то есть в точке xо достигает максимума. Аналогично доказывается утверждение данной теоремы относительно минимума функции.

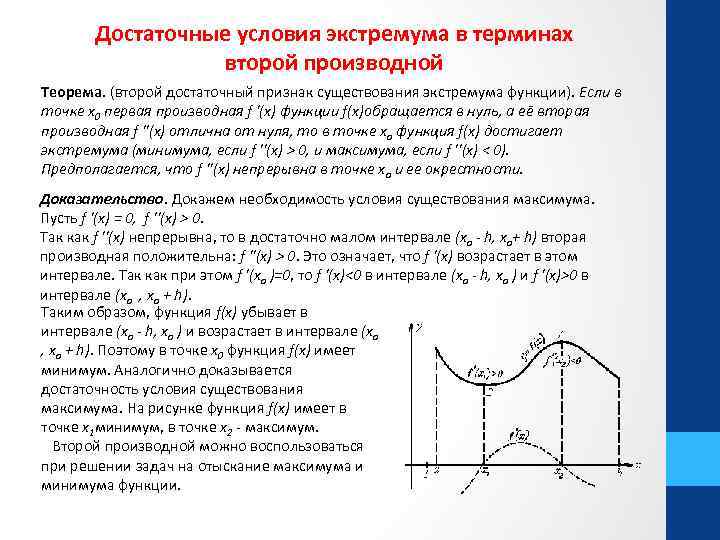Достаточные условия экстремума в терминах второй производной Теорема. (второй достаточный признак существования экстремума функции). Если в точке x 0 первая производная f '(x) функции f(x)обращается в нуль, а её вторая производная f ''(x) отлична от нуля, то в точке xо функция f(x) достигает экстремума (минимума, если f ''(x) > 0, и максимума, если f ''(x) < 0). Предполагается, что f ''(x) непрерывна в точке xо и ее окрестности. Доказательство. Докажем необходимость условия существования максимума. Пусть f '(x) = 0, f ''(x) > 0. Так как f ''(x) непрерывна, то в достаточно малом интервале (xо - h, xо+ h) вторая производная положительна: f ''(x) > 0. Это означает, что f '(x) возрастает в этом интервале. Так как при этом f '(xо )=0, то f '(x)<0 в интервале (xо - h, xо ) и f '(x)>0 в интервале (xо , xо + h). Таким образом, функция f(x) убывает в интервале (xо - h, xо ) и возрастает в интервале (xо , xо + h). Поэтому в точке x 0 функция f(x) имеет минимум. Аналогично доказывается достаточность условия существования максимума. На рисунке функция f(x) имеет в точке x 1 минимум, в точке x 2 - максимум. Второй производной можно воспользоваться при решении задач на отыскание максимума и минимума функции.

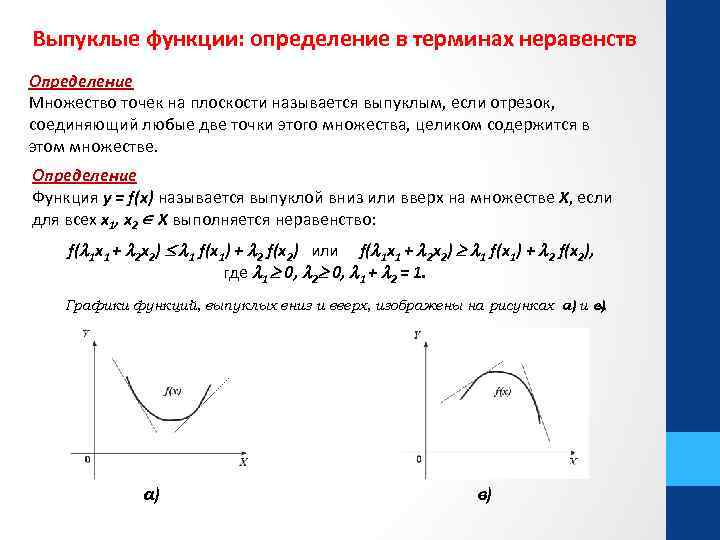Выпуклые функции: определение в терминах неравенств Определение Множество точек на плоскости называется выпуклым, если отрезок, соединяющий любые две точки этого множества, целиком содержится в этом множестве. Определение Функция y = f(x) называется выпуклой вниз или вверх на множестве X, если для всех x 1, x 2 X выполняется неравенство: f( 1 x 1 + 2 x 2) 1 f(x 1) + 2 f(x 2) или f( 1 x 1 + 2 x 2) 1 f(x 1) + 2 f(x 2), где 1 0, 2 0, 1 + 2 = 1. Графики функций, выпуклых вниз и вверх, изображены на рисунках а) и в). а) в)

Неравенство Иенсена

Неравенство Коши между средним арифметическим и средним геометрическим нескольких чисел