ad6db477b178a52014c2a7fafea35949.ppt
- Количество слайдов: 40

Monitoring Partial Order Snapshots Doron Peled Bar Ilan University, Israel & University of Warwick, UK Joint work with Peter Niebert

Monitoring an interleaving sequence n n Assume a model of execution with local events and synchronous communication. Concurrent events are monitored according to some (arbitrary) order. What are global states? What global states appear on an execution (an execution sequence)?

Bank Example n n Two branches, initially $1 M each. In one branch: deposit, $2 M. In another branch: robbery. How to model the system?
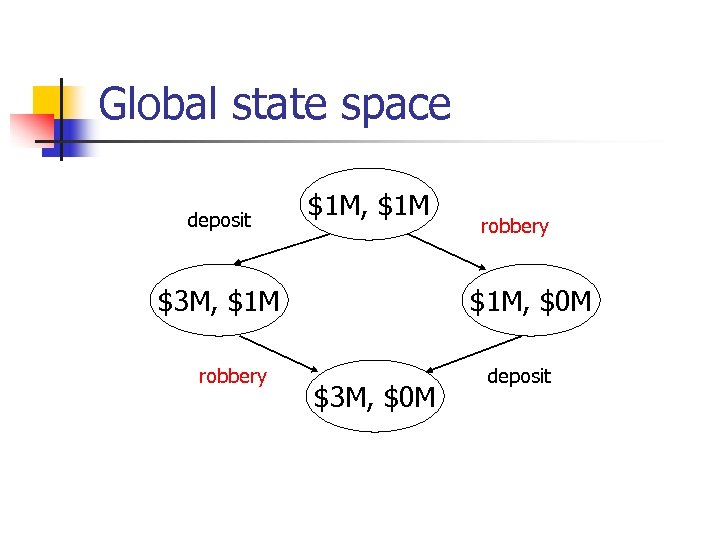
Global state space deposit $1 M, $1 M $3 M, $1 M robbery $1 M, $0 M $3 M, $0 M deposit
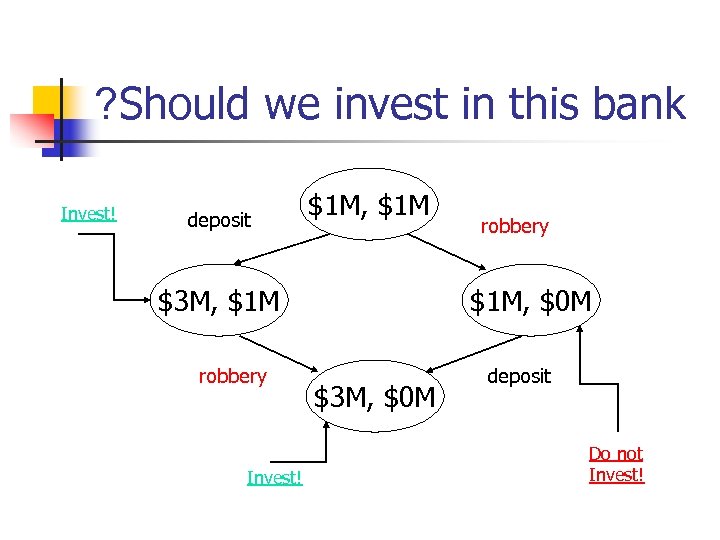
? Should we invest in this bank Invest! deposit $1 M, $1 M $3 M, $1 M robbery Invest! robbery $1 M, $0 M $3 M, $0 M deposit Do not Invest!
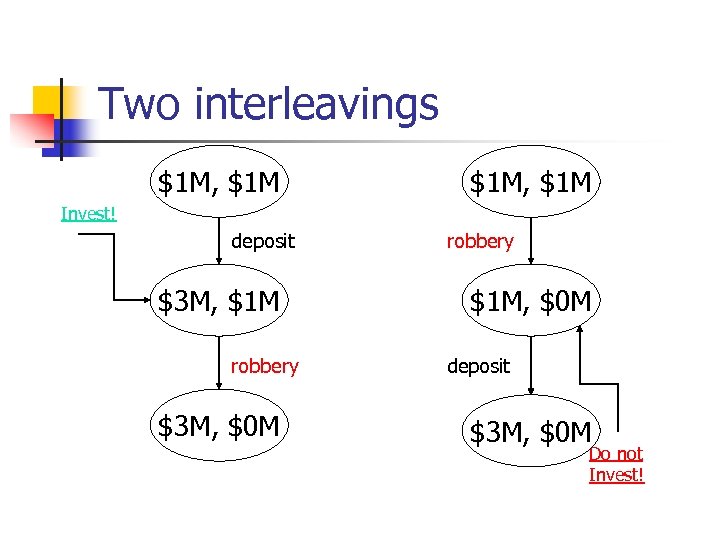
Two interleavings $1 M, $1 M Invest! deposit $3 M, $1 M robbery $3 M, $0 M robbery $1 M, $0 M deposit $3 M, $0 M Do not Invest!

Partial Order Semantics n n n n Sometimes called “real concurrency”. There is no total order between events. More intuitive. Closer to the actual behavior of the system. More difficult to analyze. Less verification results. Natural transformation between models. Partial order: (S , <), where < is n n n Transitive: x<y / y<z x<z. Antisymmetric: for no x, y, x<y / y>x. Antireflexive: for no x, x<x.

Partial Order Description $1 M deposit robbery $3 M $0 M
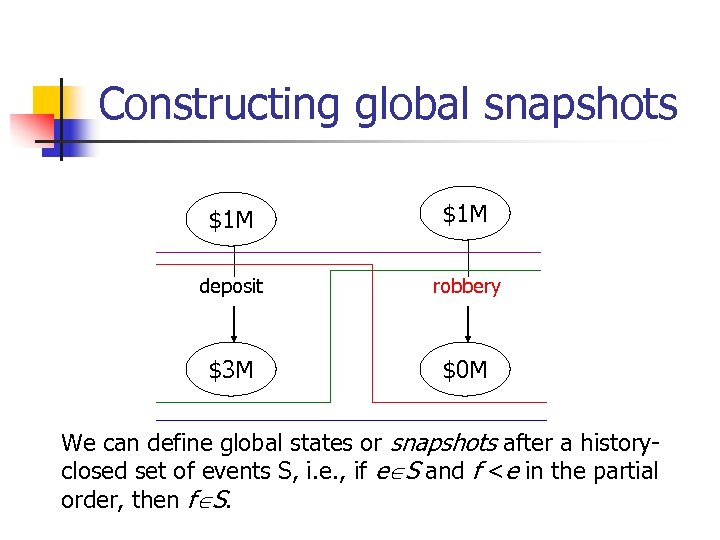
Constructing global snapshots $1 M deposit robbery $3 M $0 M We can define global states or snapshots after a historyclosed set of events S, i. e. , if e S and f <e in the partial order, then f S.
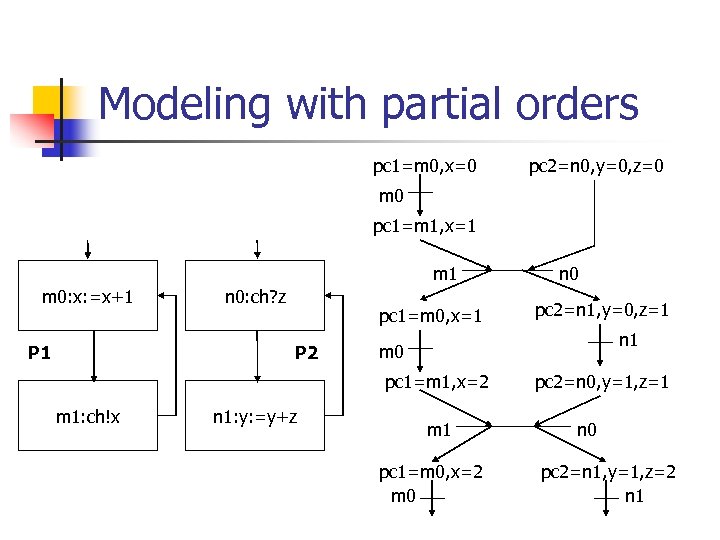
Modeling with partial orders pc 1=m 0, x=0 pc 2=n 0, y=0, z=0 m 0 pc 1=m 1, x=1 m 0: x: =x+1 P 1 n 0: ch? z pc 1=m 0, x=1 P 2 n 1: y: =y+z pc 2=n 1, y=0, z=1 n 1 m 0 pc 1=m 1, x=2 m 1: ch!x n 0 m 1 pc 1=m 0, x=2 m 0 pc 2=n 0, y=1, z=1 n 0 pc 2=n 1, y=1, z=2 n 1
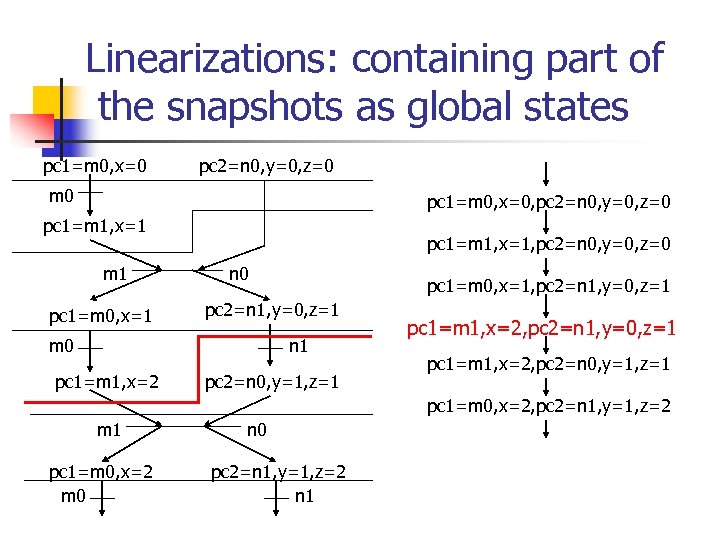
Linearizations: containing part of the snapshots as global states pc 1=m 0, x=0 pc 2=n 0, y=0, z=0 m 0 pc 1=m 0, x=0, pc 2=n 0, y=0, z=0 pc 1=m 1, x=1 m 1 pc 1=m 0, x=1 pc 1=m 1, x=1, pc 2=n 0, y=0, z=0 n 0 pc 1=m 0, x=1, pc 2=n 1, y=0, z=1 m 0 n 1 pc 1=m 1, x=2 pc 2=n 0, y=1, z=1 pc 1=m 1, x=2, pc 2=n 1, y=0, z=1 pc 1=m 1, x=2, pc 2=n 0, y=1, z=1 pc 1=m 0, x=2, pc 2=n 1, y=1, z=2 m 1 pc 1=m 0, x=2 m 0 n 0 pc 2=n 1, y=1, z=2 n 1
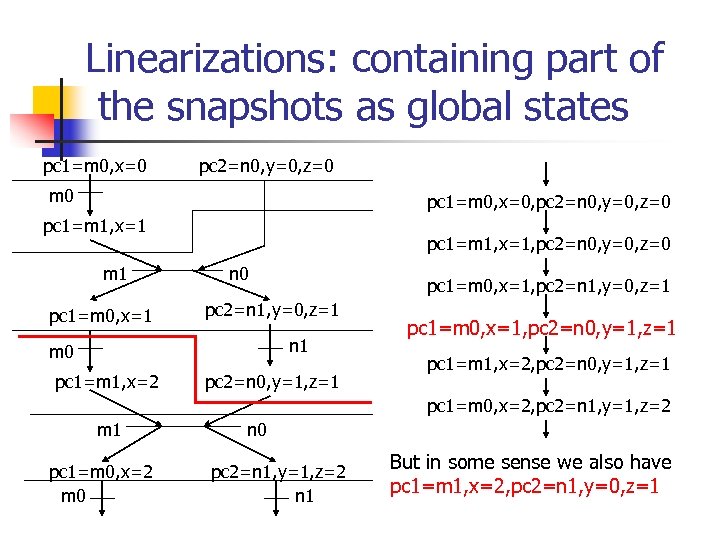
Linearizations: containing part of the snapshots as global states pc 1=m 0, x=0 pc 2=n 0, y=0, z=0 m 0 pc 1=m 0, x=0, pc 2=n 0, y=0, z=0 pc 1=m 1, x=1 m 1 pc 1=m 0, x=1 pc 1=m 1, x=1, pc 2=n 0, y=0, z=0 n 0 pc 1=m 0, x=1, pc 2=n 1, y=0, z=1 n 1 m 0 pc 1=m 1, x=2 pc 2=n 0, y=1, z=1 pc 1=m 0, x=1, pc 2=n 0, y=1, z=1 pc 1=m 1, x=2, pc 2=n 0, y=1, z=1 pc 1=m 0, x=2, pc 2=n 1, y=1, z=2 m 1 pc 1=m 0, x=2 m 0 n 0 pc 2=n 1, y=1, z=2 n 1 But in some sense we also have pc 1=m 1, x=2, pc 2=n 1, y=0, z=1
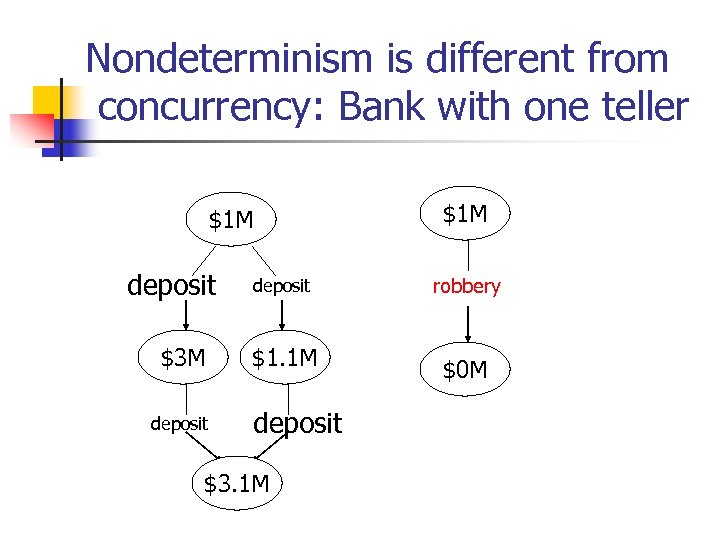
Nondeterminism is different from concurrency: Bank with one teller $1 M deposit $3 M deposit $1. 1 M deposit $3. 1 M $1 M robbery $0 M
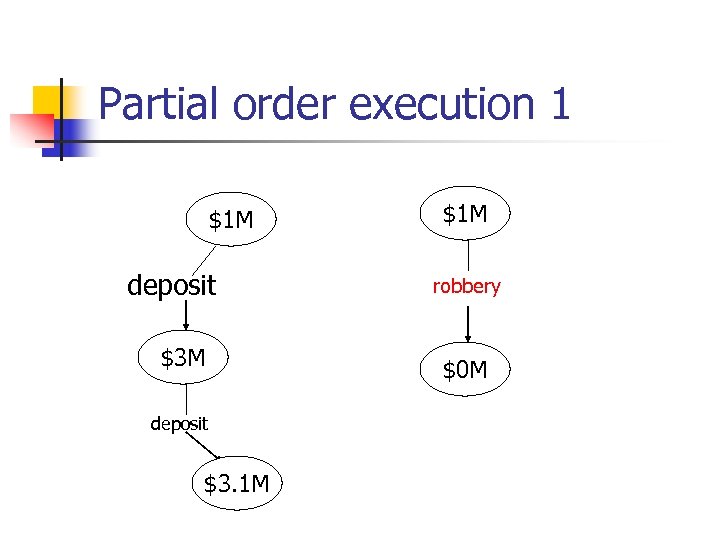
Partial order execution 1 $1 M deposit $3. 1 M $1 M robbery $0 M
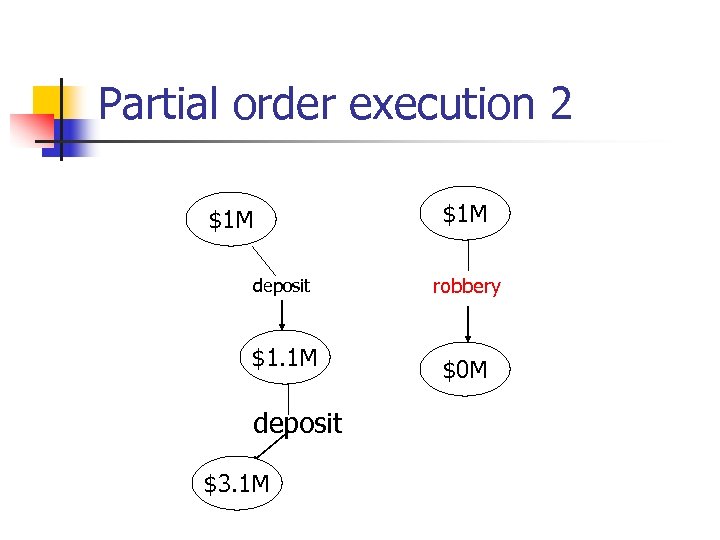
Partial order execution 2 $1 M deposit $1. 1 M deposit $3. 1 M $1 M robbery $0 M

Traces n n n An equivalence relation among sequences. Symmetric and antireflexive independence relation I ×. Example: a. Ib, a. Ic (but not b. Ic). Then we have [abac ]=[baac, abac, aabc, baca, abca, bcaa ]. Snapshots of execution [abac ] are states after [a ], [b ], [aa ], [bc ], [aab ], [abc ]. State after trace equivalent sequences, e. g. , aab, aba, baa, are the same, so we can talk about the state s[aab ] after a trace [aab ].

: In our examples n n Bank: deposit I robbery Program: m 0 I n 1 Definitions of global states using historyclosed sets of events and using trace semantics are equivalent.

Extended LTL: with snapshots The logic SLTL n n n Basic syntax as LTL. In addition, the “snapshot” operator [p], where p is a conjunction of positive and negative atomic propositions. Semantics of new operator: (u, v)|=[p] iff there exists finite sequences u 1, u 2 such that [u]=[u 1][u 2] and (u 1, u 2 v)|=p.

How to monitor executions ? and find snapshots n A deterministic automaton that keeps all the global states that are subsumed on the way.
![Automaton for prefixes of [aabc]. <s[aa] , >, <s[a], {a}>, <s[], {a}> a a Automaton for prefixes of [aabc]. <s[aa] , >, <s[a], {a}>, <s[], {a}> a a](https://present5.com/presentation/ad6db477b178a52014c2a7fafea35949/image-20.jpg)
Automaton for prefixes of [aabc]. <s[aa] , >, <s[a], {a}>, <s[], {a}> a a <s[a], >, <s[], {a}> b <s[], > b <s[b], >, <s[], {b}> a <s[ab], >, <s[b], {a}>, <s[a], {b}>, <s[], {a, b}> c <s[bc], >, <s[b], {c}>, <s[], {b, c}> a c a b <s [aab], >, <s [ab], {a}>, <s [b]. {a}>, <s [a], {a, b}> <s[abc], >, <s [ab], {c}> <s[b], {a, c}>, <s[a], {b, c}>, <s[], {a, b, c}> a c <s[aabc], >, <s[abc], {a}>, <s[aab], {c}> <s[bc], {a}>, <s[ab], {a, c}> <s[aa], {b, c}>, <s[a], {a, b}>, <s[], {a, b}>

How to construct this ? automaton n n Each node consists of a set of pairs <s, A>, where s is a (subsumed) state and A is a subset of actions. It denotes that s is a subsumed state, and it takes the actions A (with possible repetitions) in some order to reach the current state.
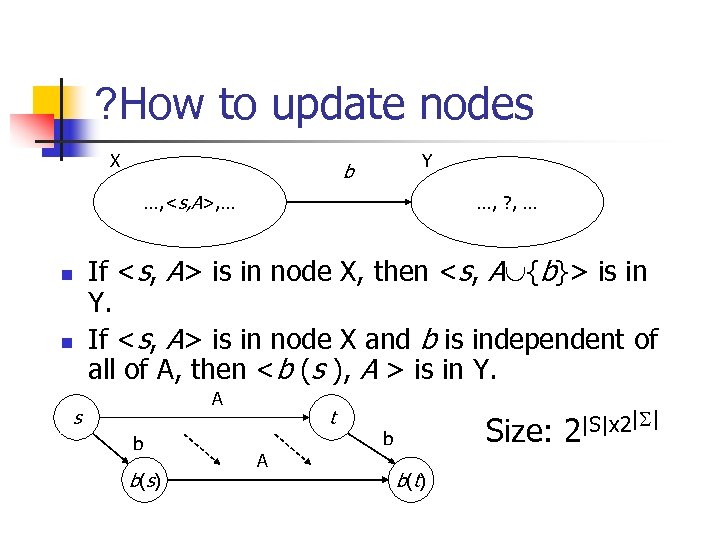
? How to update nodes X Y b …, <s, A>, … n n …, ? , … If <s, A> is in node X, then <s, A {b}> is in Y. If <s, A> is in node X and b is independent of all of A, then <b (s ), A > is in Y. A s b b ( s) t A Size: b b ( t) |S|x 2| | 2

: We make a restriction n Each process Pi will have its own set of propositions, related to the local states of Pi. We can write in […] only a conjunction of local properties q 1/q 2/. . . /qn. Freeze set: a subset of processes that satisfy the corresponding part of local properties. (We can also keep the actual local states with the processes. )
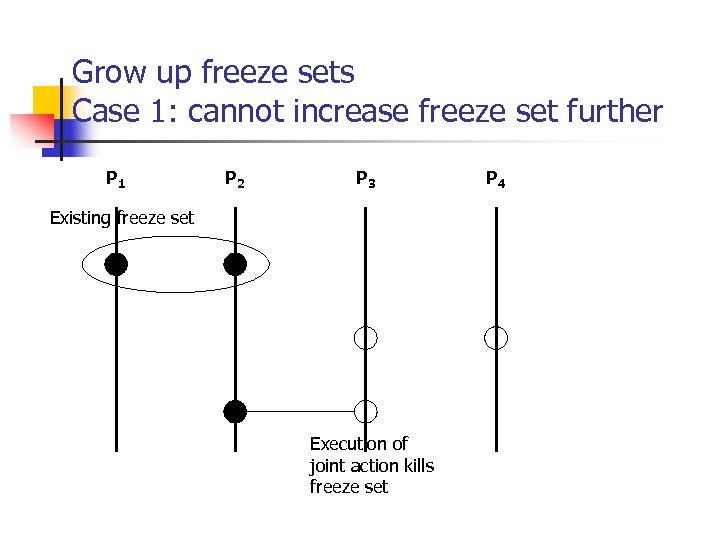
Grow up freeze sets Case 1: cannot increase freeze set further P 1 P 2 P 3 Existing freeze set Execution of joint action kills freeze set P 4
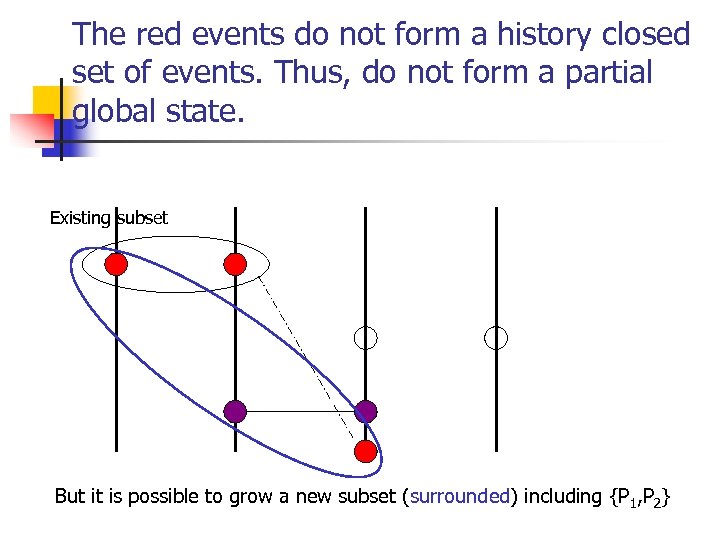
The red events do not form a history closed set of events. Thus, do not form a partial global state. Existing subset But it is possible to grow a new subset (surrounded) including {P 1, P 2}
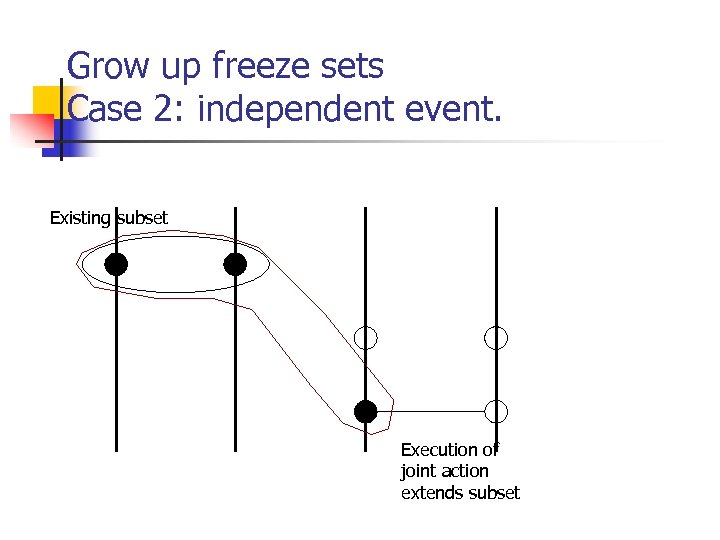
Grow up freeze sets Case 2: independent event. Existing subset Execution of joint action extends subset
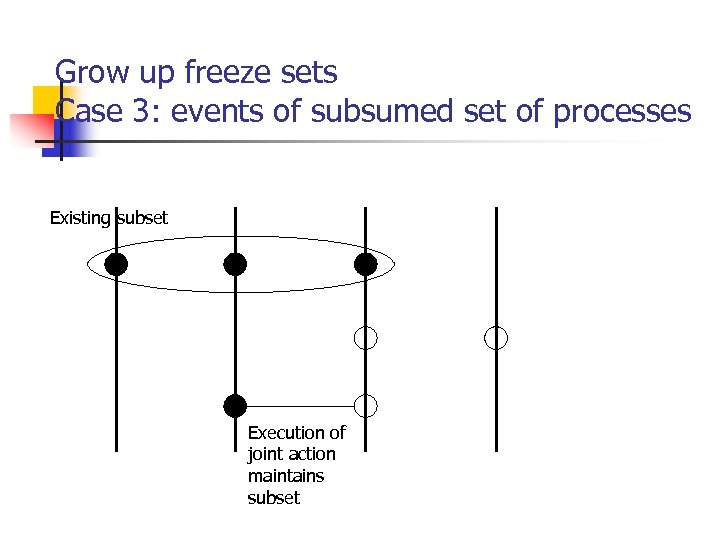
Grow up freeze sets Case 3: events of subsumed set of processes Existing subset Execution of joint action maintains subset

: Can be formulated as follows n n proc(a) – the set of processes where action a participates. addproc(s, a) – when executing action a from state s, these are the local states from proc(a) that satisfy the local propositions that we check. Extension: Let F 1 addproc(s, a) and F 2 existing subset such that F 2 proc(a)=. Then extend F 1 into F 1 F 2. Propagation: For existing subset F such that proc(a) F, we maintain F.
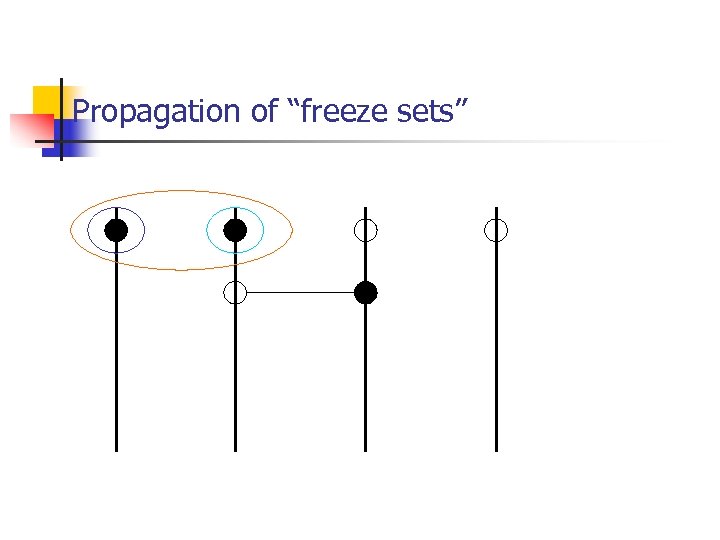
Propagation of “freeze sets”
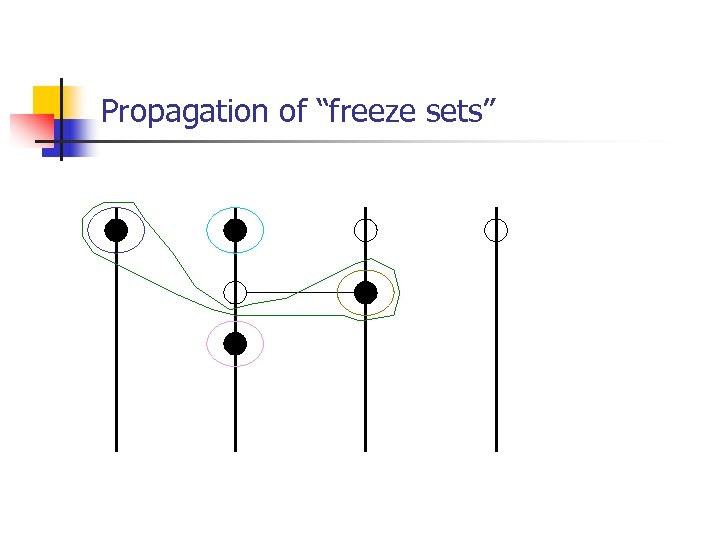
Propagation of “freeze sets”
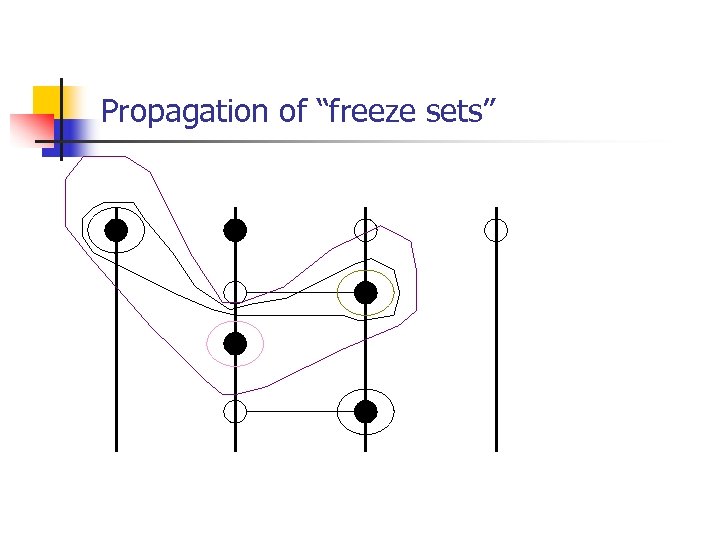
Propagation of “freeze sets”
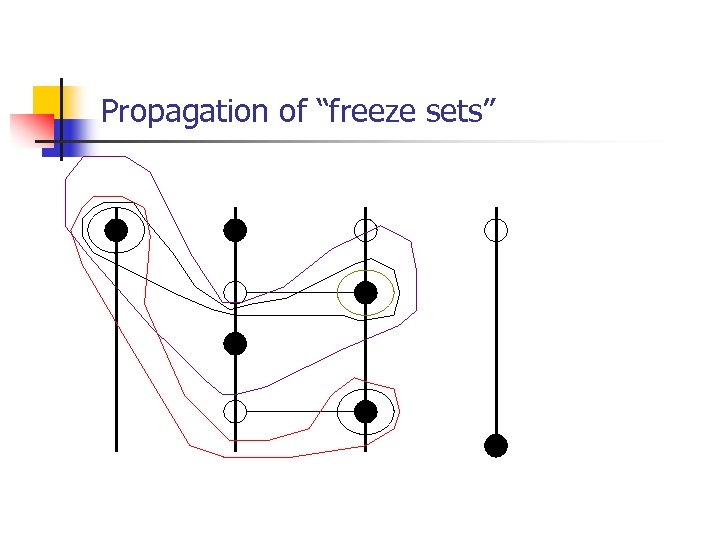
Propagation of “freeze sets”
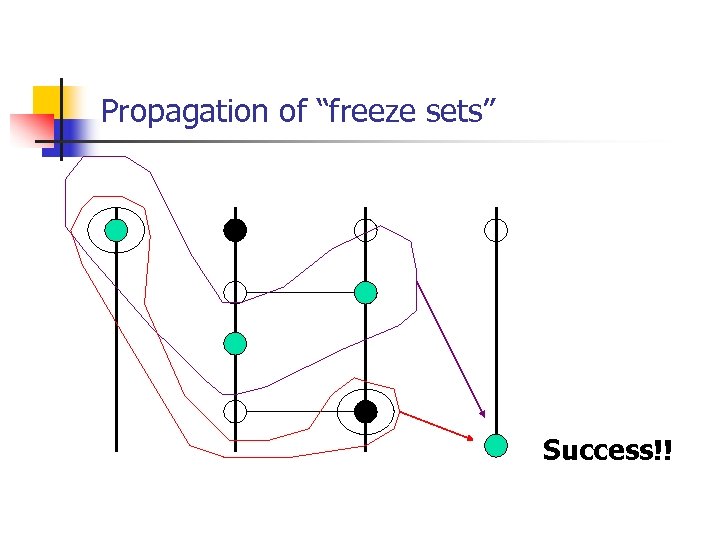
Propagation of “freeze sets” Success!!

? How to store efficiently n n Freeze sets T closed under union and intersection. Need to store only a basis B of T, where unions are not included. In this case, size of basis is not larger than number of elements. Update of basis is polynomial.
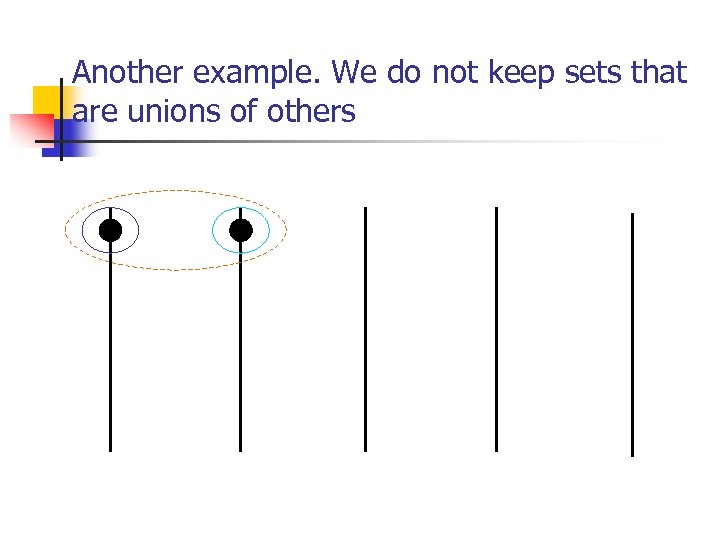
Another example. We do not keep sets that are unions of others
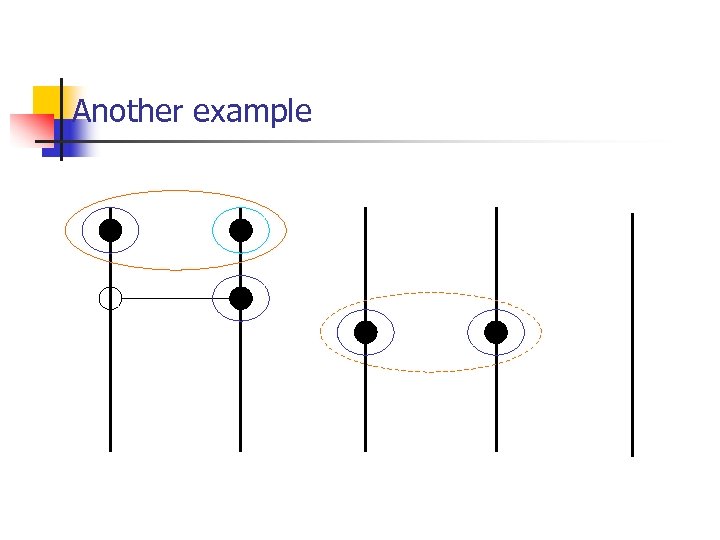
Another example
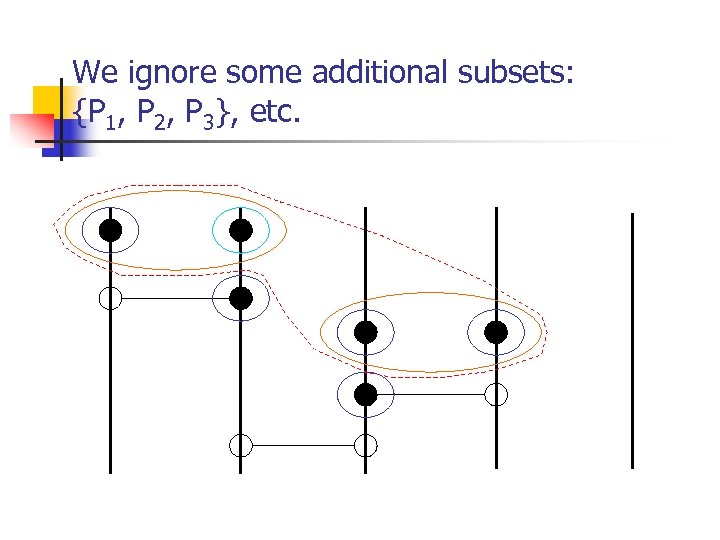
We ignore some additional subsets: {P 1, P 2, P 3}, etc.
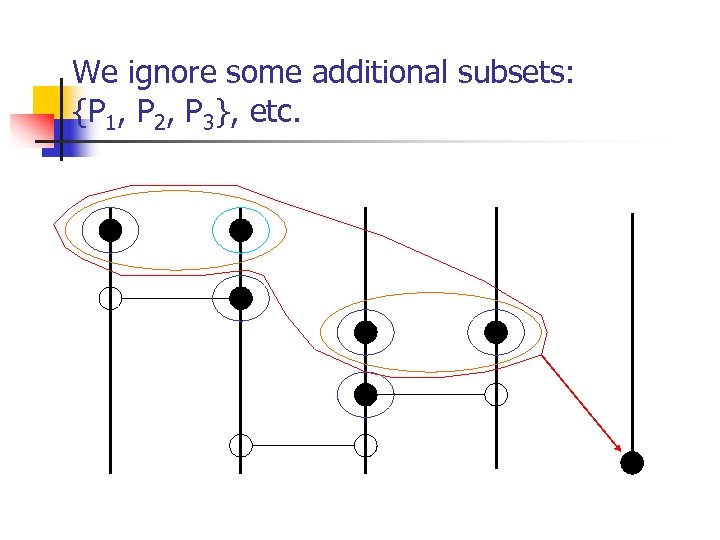
We ignore some additional subsets: {P 1, P 2, P 3}, etc.

How to perform model ? checking n n Construct an automaton for A¬ as usual. Construct an automaton for each conjunction that appears inside the […] operator to run in parallel. Binary search is still polynomial in number of processes and size of formula!

Conclusions n n n Added capability of partial orders into LTL specification. Freeze sets construction for detecting global states that are subsumed during execution. Model checking is basically same complexity as for normal LTL!
ad6db477b178a52014c2a7fafea35949.ppt