c0c41c60948fd4f66f60d2d133df82af.ppt
- Количество слайдов: 70

MONADIC QUERIES over TREE-STRUCTURED DATA Georg Gottlob TU Wien & Oxford University Joint work with Christoph Koch, Robert Baumgartner, and Marcus Herzog, and Reinhard Pichler

Talk Outline • • • Semistructured data HTML, XML Monadic Queries Monadic datalog over trees Xpath Web information extraction (wrapping) Lixto

Strings, Trees, Graphs, & Logic A few well-known results: • Büchi: MSO=REG over strings • Rabin: decidability of S 2 S • Thatcher and Wright: MSO = REG over ranked trees (tree automata) • Brüggemann-Klein/Wood/Murata: MSO = REG over unranked trees • Fagin: ESO = NP Note: over graphs ESO NP-hard, MSO hard for Pol. Hierarchy. • Grädel/Immerman/Vardi: ESO(Horn)=Datalog=LFP=PTIME (on ordered structures) • Courcelle MSO in Lin. Time on tree-like structures (treewidth <= k) • Clarke, Emerson, Pnueli, et al: CTL, LTL …

Web documents are trees ! HTML: Hypertext Markup Language XML: Extensible Markup Language HTML, XML: Context free languages. Represent a document by its parse tree. Tags: vertex labels Labeled trees.
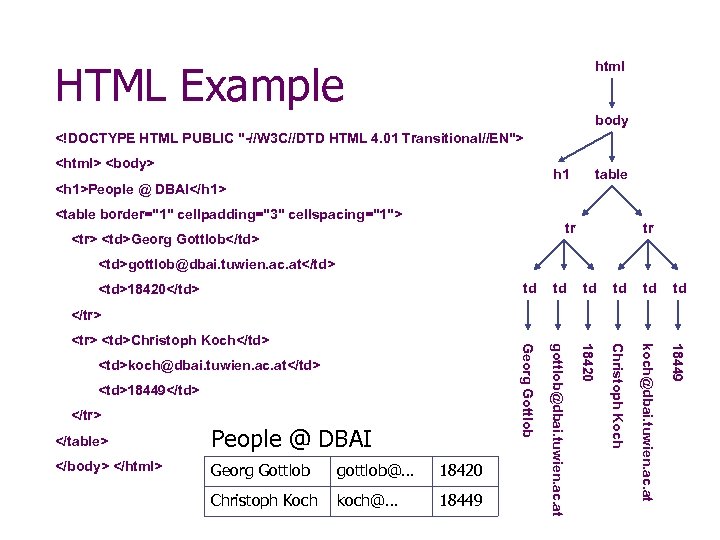
HTML Example html body <!DOCTYPE HTML PUBLIC "-//W 3 C//DTD HTML 4. 01 Transitional//EN"> <html> <body> h 1 <h 1>People @ DBAI</h 1> <table border="1" cellpadding="3" cellspacing="1"> table tr <tr> <td>Georg Gottlob</td> tr <td>gottlob@dbai. tuwien. ac. at</td> td td td Georg Gottlob gottlob@dbai. tuwien. ac. at 18420 Christoph Koch koch@dbai. tuwien. ac. at 18449 <td>18420</td> </tr> <td>Christoph Koch</td> <td>koch@dbai. tuwien. ac. at</td> <td>18449</td> </tr> </table> People @ DBAI </body> </html> Georg Gottlob gottlob@… 18420 Christoph Koch koch@… 18449
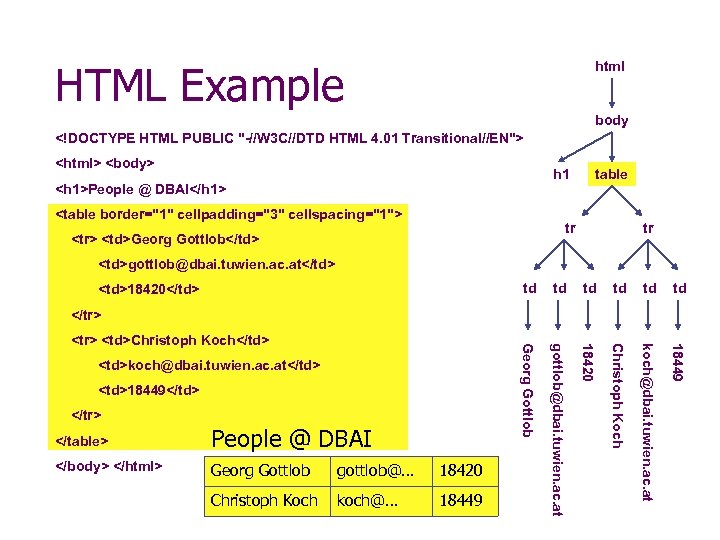
HTML Example html body <!DOCTYPE HTML PUBLIC "-//W 3 C//DTD HTML 4. 01 Transitional//EN"> <html> <body> h 1 <h 1>People @ DBAI</h 1> <table border="1" cellpadding="3" cellspacing="1"> table tr <tr> <td>Georg Gottlob</td> tr <td>gottlob@dbai. tuwien. ac. at</td> td td td Georg Gottlob gottlob@dbai. tuwien. ac. at 18420 Christoph Koch koch@dbai. tuwien. ac. at 18449 <td>18420</td> </tr> <td>Christoph Koch</td> <td>koch@dbai. tuwien. ac. at</td> <td>18449</td> </tr> </table> People @ DBAI </body> </html> Georg Gottlob gottlob@… 18420 Christoph Koch koch@… 18449
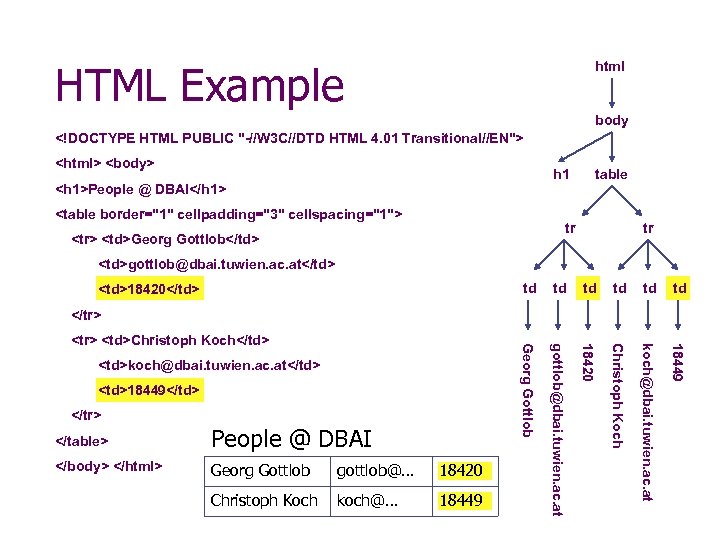
HTML Example html body <!DOCTYPE HTML PUBLIC "-//W 3 C//DTD HTML 4. 01 Transitional//EN"> <html> <body> h 1 <h 1>People @ DBAI</h 1> <table border="1" cellpadding="3" cellspacing="1"> table tr <tr> <td>Georg Gottlob</td> tr <td>gottlob@dbai. tuwien. ac. at</td> td td td Georg Gottlob gottlob@dbai. tuwien. ac. at 18420 Christoph Koch koch@dbai. tuwien. ac. at 18449 <td>18420</td> </tr> <td>Christoph Koch</td> <td>koch@dbai. tuwien. ac. at</td> <td>18449</td> </tr> </table> People @ DBAI </body> </html> Georg Gottlob gottlob@… 18420 Christoph Koch koch@… 18449
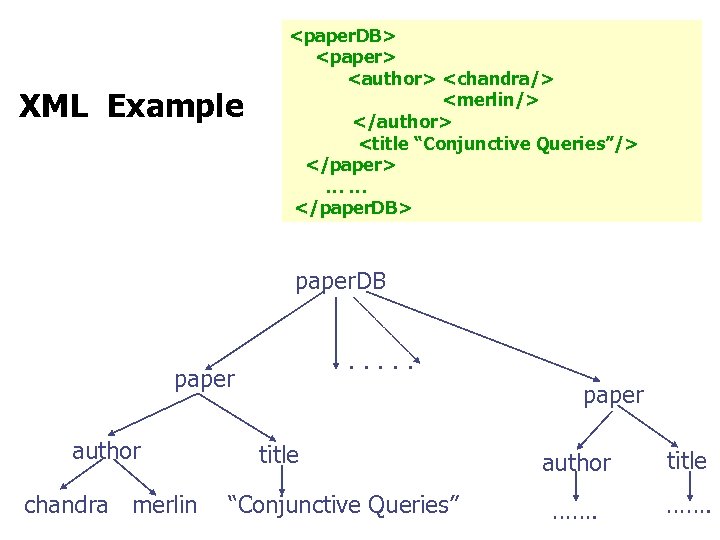
XML Example <paper. DB> <paper> <author> <chandra/> <merlin/> </author> <title “Conjunctive Queries”/> </paper> …… </paper. DB> paper. DB. . . paper author chandra merlin paper title “Conjunctive Queries” author title …….
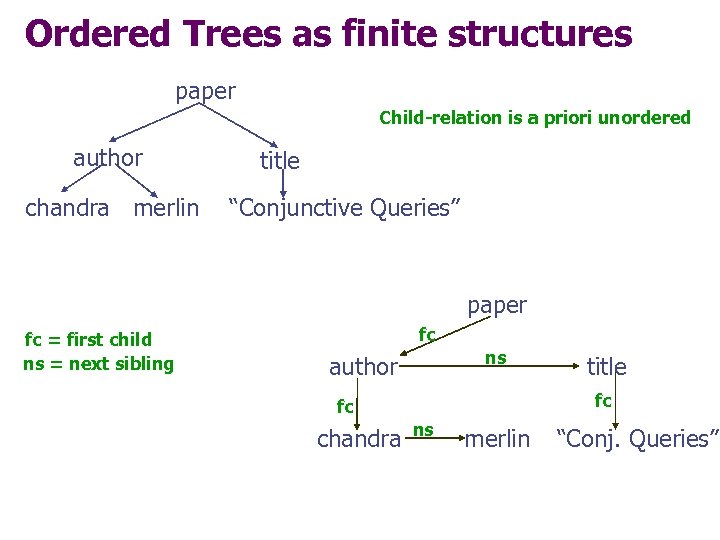
Ordered Trees as finite structures paper Child-relation is a priori unordered author chandra merlin title “Conjunctive Queries” paper fc = first child ns = next sibling fc ns author fc fc chandra title ns merlin “Conj. Queries”

Core XPath w simple location steps paper/title w loc. steps with explicit axes paper/descendant: : merlin w qualifiers paper[…. . ] w Boolean logic. . . [chandra and merlin and (not harel)] Full Xpath: + node set comparisons and operations + order functions (first, last, position) , etc. + arithmetic and string operations Implementations: in the context of XSLT processors Xalan, XT, MS Internet Explorer (IE 6)
![XPath Examples /descendant: : a/child: : b[ descendant: : c and not(following-sibling: : d)] XPath Examples /descendant: : a/child: : b[ descendant: : c and not(following-sibling: : d)]](https://present5.com/presentation/c0c41c60948fd4f66f60d2d133df82af/image-11.jpg)
XPath Examples /descendant: : a/child: : b[ descendant: : c and not(following-sibling: : d)] c a /descendant: : a/child: b[ following-sibling: : d] a b b d b c a c a a c b b c d b b b c c d b c
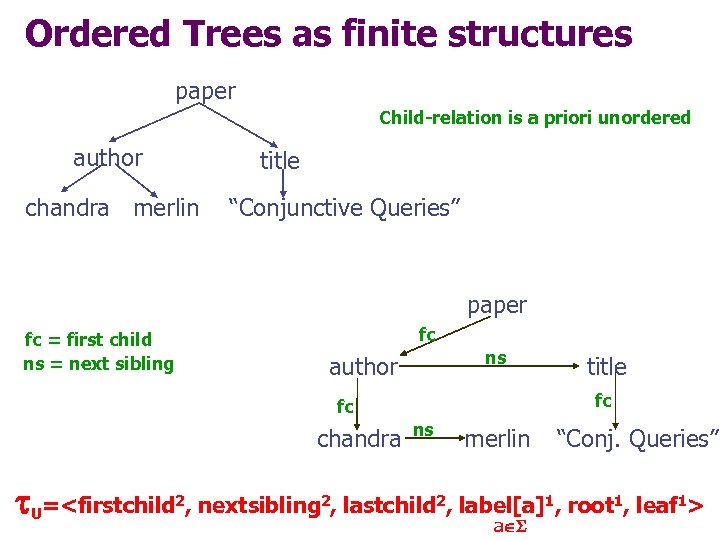
Ordered Trees as finite structures paper Child-relation is a priori unordered author chandra merlin title “Conjunctive Queries” paper fc = first child ns = next sibling fc ns author fc fc chandra title ns merlin “Conj. Queries” U=<firstchild 2, nextsibling 2, lastchild 2, label[a]1, root 1, leaf 1> a

Monadic Queries over Trees Select some nodes of a tree Unary query f: Trees 2 dom No Joins or combinations of objects Yardstick: Monadic Second Order Logic (MSO) Select titles of articles authored by Chandra and Merlin Two important applications: • Web Information Extraction ( later) • Monadic XML Queries

Monadic Datalog over Trees paper. DB fc ns paper ns fc ns author fc fc chandra title ns merlin “Conj. Queries” Select titles of articles authored By Chandra and Merlin
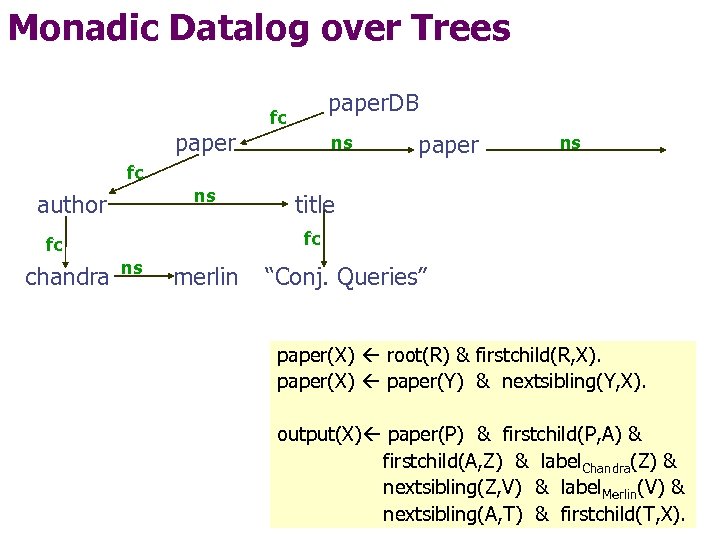
Monadic Datalog over Trees paper. DB fc ns paper ns fc ns author fc fc chandra title ns merlin “Conj. Queries” paper(X) root(R) & firstchild(R, X). paper(X) paper(Y) & nextsibling(Y, X). output(X) paper(P) & firstchild(P, A) & firstchild(A, Z) & label. Chandra(Z) & nextsibling(Z, V) & label. Merlin(V) & nextsibling(A, T) & firstchild(T, X).

How expressive is monadic Datalog? It was known that: w. Monadic Datalog 1 -MSO w. Full Datalog = P Theorem [G. & Koch 2002]: Over U, Monadic Datalog = MSO A unary query is definable in MSO iff it is definable via a monadic datalog program.

Proof idea: Simulate Unranked Query Automata (UQA) by Neven and Schwentick in mon. Datalog UQA Unary MSO Queries [Neven & Schwentick 01]
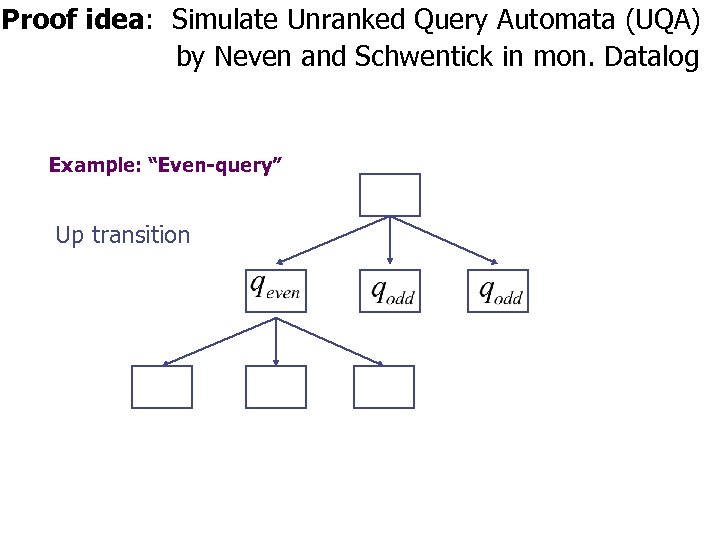
Proof idea: Simulate Unranked Query Automata (UQA) by Neven and Schwentick in mon. Datalog Example: “Even-query” Up transition
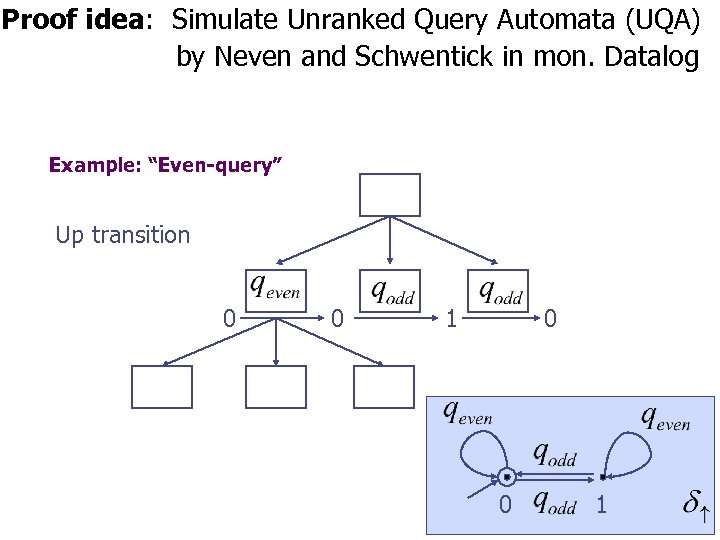
Proof idea: Simulate Unranked Query Automata (UQA) by Neven and Schwentick in mon. Datalog Example: “Even-query” Up transition 0 0 1
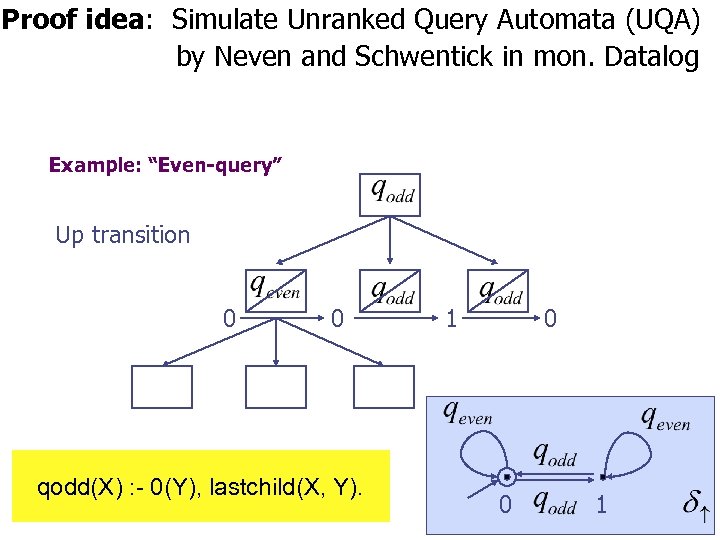
Proof idea: Simulate Unranked Query Automata (UQA) by Neven and Schwentick in mon. Datalog Example: “Even-query” Up transition 0 0 qodd(X) : - 0(Y), lastchild(X, Y). 1 0 0 1

How complex is Monadic Datalog? Previously known facts on full Datalog over Graphs: w Data Complexity of Datalog: P-complete (impl. in [Vardi 88]) w Combined Complexity EXPTIME-complete (impl. [Vardi 88]) w Comb. Compl. of sirups: EXPTIME-cplt. ([G. &Papadimitriou 99]) Theorem [G. & Koch 2002]: Monadic Datalog over U has combined complexity: O(|data|*|query|) Data Complexity: P-complete and linear-time.

Proof idea: 1. ) Transform datalog program + input tree in linear time into a “ground” propositional logic program • Exploit functional dependencies: nextsibling(X, Y) has only a linear number of ground instances: nextsibling(ni, nj), etc. • Decouple independent atoms of rule bodies p(X) q(X) & r(Y) & nextsibling(X, Z) & s(Z). p(X) q(X) & r & nextsibling(X, Z) & s(Z). r r(Y). 2. ) Execute ground program in linear time by using well-known algorithms: [Dowling&Gallier] [Minoux]
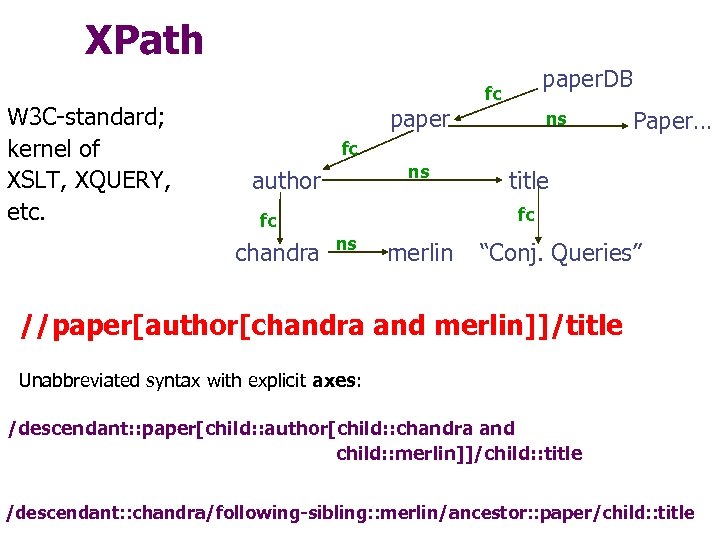
XPath W 3 C-standard; kernel of XSLT, XQUERY, etc. paper. DB fc ns Paper… fc ns author fc fc chandra title ns merlin “Conj. Queries” //paper[author[chandra and merlin]]/title Unabbreviated syntax with explicit axes: /descendant: : paper[child: : author[child: : chandra and child: : merlin]]/child: : title /descendant: : chandra/following-sibling: : merlin/ancestor: : paper/child: : title
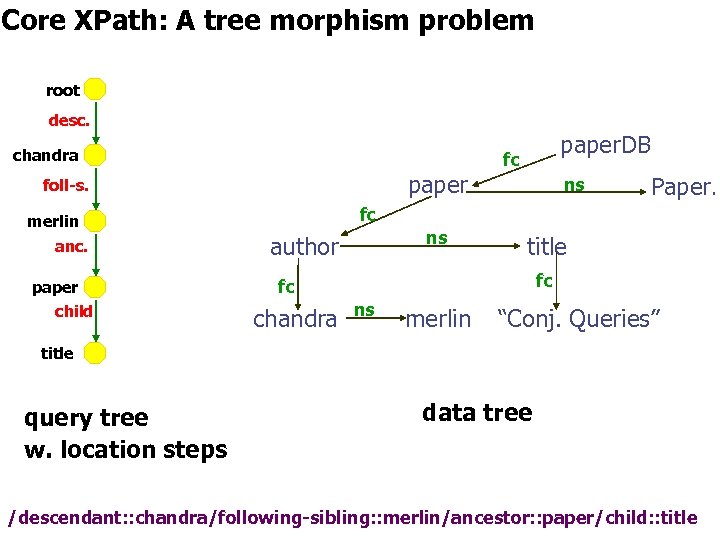
Core XPath: A tree morphism problem root desc. chandra paper foll-s. paper child ns Paper… fc merlin anc. paper. DB fc ns author title fc fc chandra ns merlin “Conj. Queries” title query tree w. location steps data tree /descendant: : chandra/following-sibling: : merlin/ancestor: : paper/child: : title
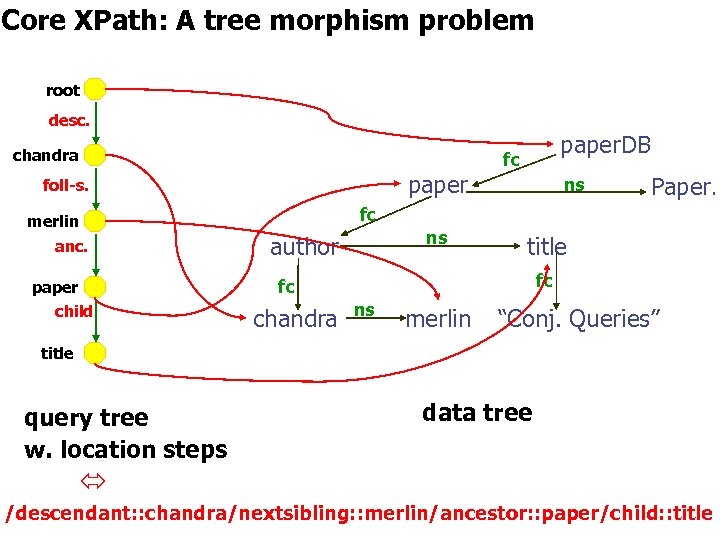
Core XPath: A tree morphism problem root desc. chandra paper foll-s. paper child ns Paper… fc merlin anc. paper. DB fc ns author title fc fc chandra ns merlin “Conj. Queries” title query tree w. location steps data tree /descendant: : chandra/nextsibling: : merlin/ancestor: : paper/child: : title

Core XPath w simple location steps paper/title w loc. steps with explicit axes paper/descendant: : merlin w qualifiers paper[…. . ] w Boolean logic. . . [chandra and merlin and (not harel)] Full Xpath: + node set comparisons and operations + order functions (first, last, position) , etc. + arithmetic and string operations Implementations: in the context of XSLT processors Xalan, XT, MS Internet Explorer (IE 6)

Core XPath w simple location steps paper/title w loc. steps with explicit axes paper/descendant: : merlin w qualifiers paper[…. . ] w Boolean logic. . . [chandra and merlin and (not harel)] Full Xpath: + node set comparisons and operations + order functions (first, last) , etc. + arithmetic and string operations Implementations: Xalan, XT, MS Internet Explorer 6 (IE 6) Complexity, efficiency? [G. , Koch, Pichler, VLDB 02]
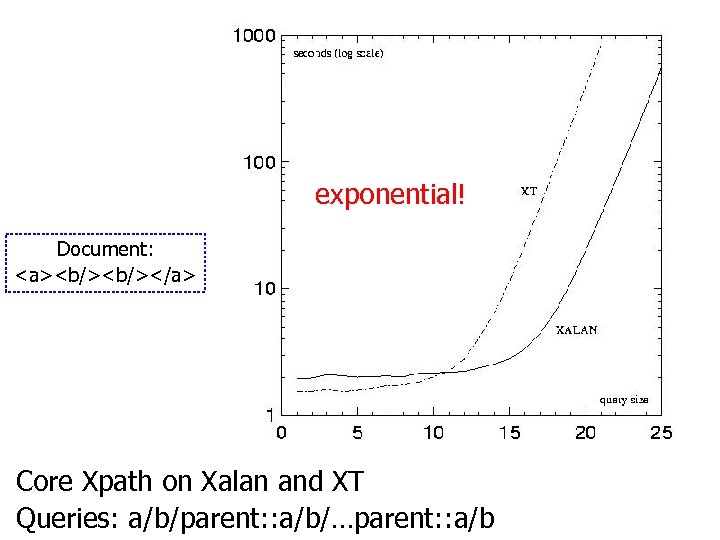
exponential! Document: <a><b/></a> Core Xpath on Xalan and XT Queries: a/b/parent: : a/b/…parent: : a/b
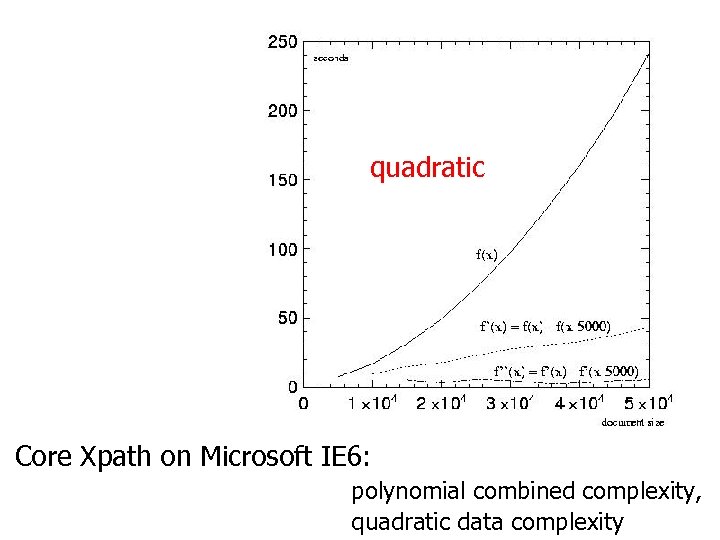
quadratic Core Xpath on Microsoft IE 6: polynomial combined complexity, quadratic data complexity
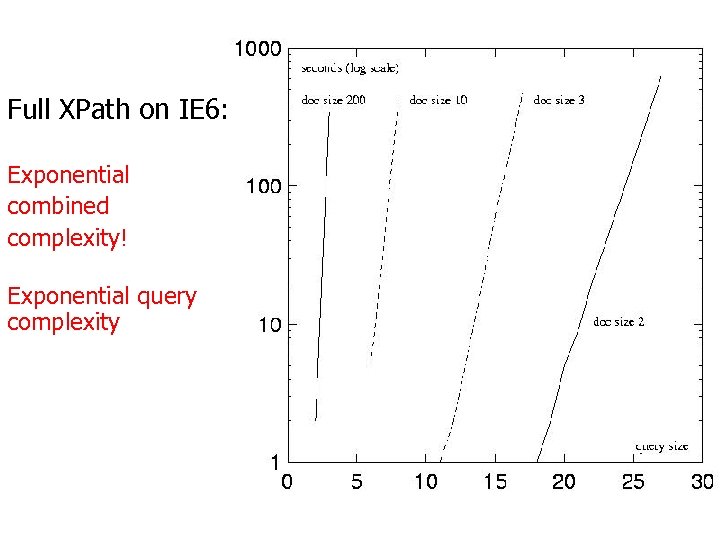
Full XPath on IE 6: Exponential combined complexity! Exponential query complexity

Axes and regular expressions Observation: All XPath Axes can be expressed as regular expression of U-axes firstchild and nextsibling: child : = firstchild. nextsibling* parent : = (nextsibling-1)*. firstchild-1 descendant : = firstchild. (firstchild nextsibling)* etc … General Definition of “axis” : Relation definable via a regular expression (with inversion) from the primitive relations of U

Conjunctive queries with axes CQ: Example: conjunction of U-atoms and of atoms corresponding to derived axes nextsibling(X, Z) & descendant(Z, U) & ancestor(U, V) & labela (V) & child(V, X) & (firstchild-1)(U, X) Theorem: Evaluating conjunctive queries with axes over trees is NP-complete (query complexity)

Conjunctive queries with axes CQ: Example: conjunction of U-atoms and of atoms corresponding to derived axes nextsibling(X, Z) & descendant(Z, U) & ancestor(U, V) & labela (V) & child(V, X) & (firstchild-1)(U, X) Theorem: Evaluating conjunctive queries with axes over trees is NP-complete (query complexity) However: XPath more akin acyclic conjunctive queries!

Acyclic conjunctive queries with axes Theorem: Evaluating acyclic conjunctive queries with axes over trees is feasible in time O(|data|*|query|) Proof idea: translate acyclic qery into monadic datalog program over U child(A, X) descendant(X, Y) descendant(Y, Z) labelb(Y) labela(Z)

Acyclic conjunctive queries with axes Theorem: Evaluating acyclic conjunctive queries with axes over trees is feasible in time O(|data|*|query|) Proof idea: translate acyclic qery into monadic datalog program over U child(A, X) descendant(X, Y) descendant(Y, Z) labelb(Y) labela(Z) Ear atom which contains an ear variable that otherwise occurs in monadic atoms only. Is definable as (unary) MSO-query and thus expressible by a monadic datalog program.
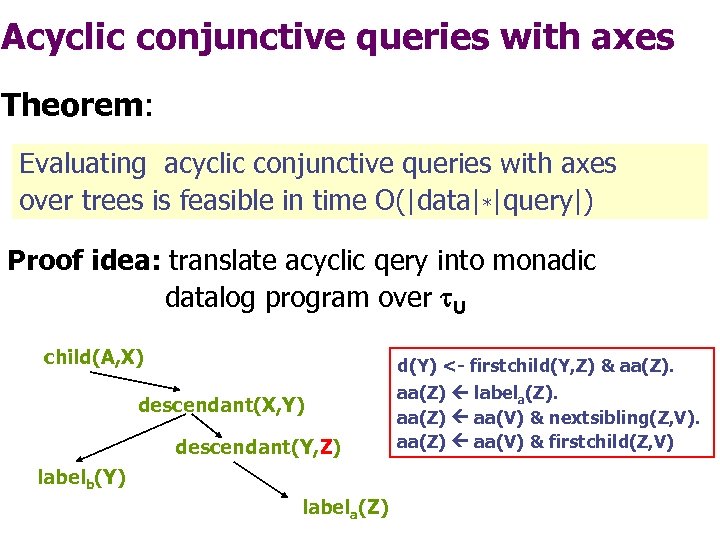
Acyclic conjunctive queries with axes Theorem: Evaluating acyclic conjunctive queries with axes over trees is feasible in time O(|data|*|query|) Proof idea: translate acyclic qery into monadic datalog program over U child(A, X) d(Y) <- firstchild(Y, Z) & aa(Z). descendant(X, Y) descendant(Y, Z) labelb(Y) labela(Z) aa(Z) labela(Z). aa(Z) aa(V) & nextsibling(Z, V). aa(Z) aa(V) & firstchild(Z, V)

Acyclic conjunctive queries with axes Theorem: Evaluating acyclic conjunctive queries with axes over trees is feasible in time O(|data|*|query|) Proof idea: translate acyclic qery into monadic datalog program over U child(A, X) d(Y) <- firstchild(Y, Z) & aa(Z). descendant(X, Y) labelb(Y) d(Y) aa(Z) labela(Z). aa(Z) aa(V) & nextsibling(Z, V). aa(Z) aa(V) & firstchild(Z, V)

Acyclic conjunctive queries with axes Theorem: Evaluating acyclic conjunctive queries with axes over trees is feasible in time O(|data|*|query|) Proof idea: translate acyclic qery into monadic datalog program over U Ear atom. child(A, X) descendant(X, Y) labelb(Y) d(Y) Continue eliminating ear atoms until query is entirely monadic.

Acyclic Monadic Datalog with Axes AMX-Datalog: monadic datalog programs whose rule bodies are acyclic and may contain arbitrary axes Theorem: Evaluating AMX-datalog programs over trees is feasible in time O(|data|*|program|) Remarks: • Same bound for stratified AMX-Datalog • AMX-Datalog expresses MSO over U (both without and with stratification)

Core XPath in Linear Time Corollary: Evaluating core-XPath queries over trees is feasible in time O(|data|*|query|) Proof: Linear translation from Core XPath to stratified Monadic Datalog + axes

Core XPath in Linear Time Corollary: Evaluating core-XPath queries over trees is feasible in time O(|data|*|query|) //paper[author[chandra and not merlin]]/title output(X) root(R) & descendant(R, P) & labelpaperr(P) & qual 1(P) & child(P, X) & labeltitle(X). qual 1(X) child(X, Y) & labelauthor(Y) & qual 2(Y). qual 2(X) child(X, Y) & labelchandra(Y) & not qual 3(X) child(X, M) & labelmerlin(M).
![Full XPath in Polynomial Time Theorem [G. , Koch, Pichler, VLDB 2002]: Evaluating full Full XPath in Polynomial Time Theorem [G. , Koch, Pichler, VLDB 2002]: Evaluating full](https://present5.com/presentation/c0c41c60948fd4f66f60d2d133df82af/image-42.jpg)
Full XPath in Polynomial Time Theorem [G. , Koch, Pichler, VLDB 2002]: Evaluating full XPath queries over XML documents is feasible in polynomial time (combined complexity) Proof: Extends the Logic Programming evaluation paradigm to all “nasty” features of full XPath. Implementation (main memory): XML-Taskforce XPath To our knowledge the only XPath system that scales.
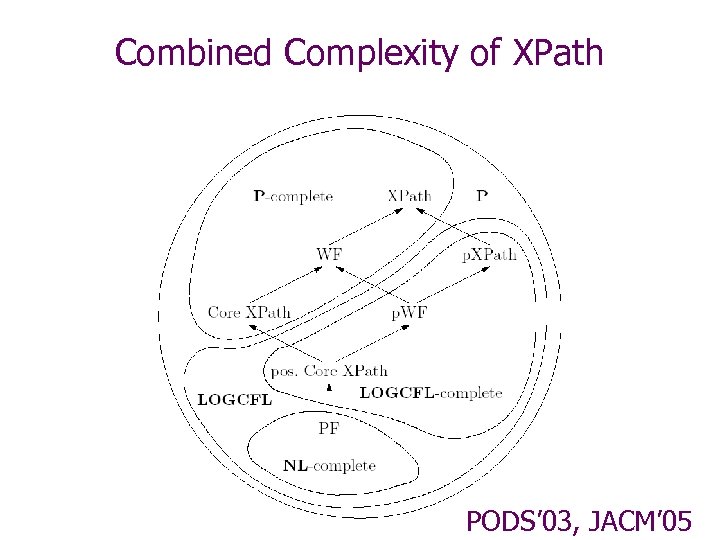
Combined Complexity of XPath PODS’ 03, JACM’ 05

Data and Query Complexity XPath PF L-complete (NC 1 -red. ) L Data complexity Theorem. XPath is in L (data complexity). Theorem. PF is L-hard under NC 1 -reductions (data complexity). Theorem. XPath w/o multiplication, concatenation is in L w. r. t. query complexity.

Core XPath and CTL Straightforward translation from Core XPath with vertical axes to CTL with past modalities. (On graphs with child relation – order independent!) //paper[author[chandra and merlin]]/title first normalize to: //title[parent: : paper[author[chandra and merlin]]] title & EX-1(paper & EX(author & EXchandra & EXmerlin)) Core XPath requires multimodal CTL: X , etc.

General conjunctive queries with axes We know they are NP-complete, but… Research programme: • Find interesting sets of axes for which CQs are tractable. • Trace the “tractablity frontier”, i. e. , determine all maximal sets of axes for which CQs are tractable. • Extend tractability results to datalog. PODS 2004: G. , Koch, Schulz: Solved for all XPath axes

Cyclic Query Example (from Computational. Linguistics)
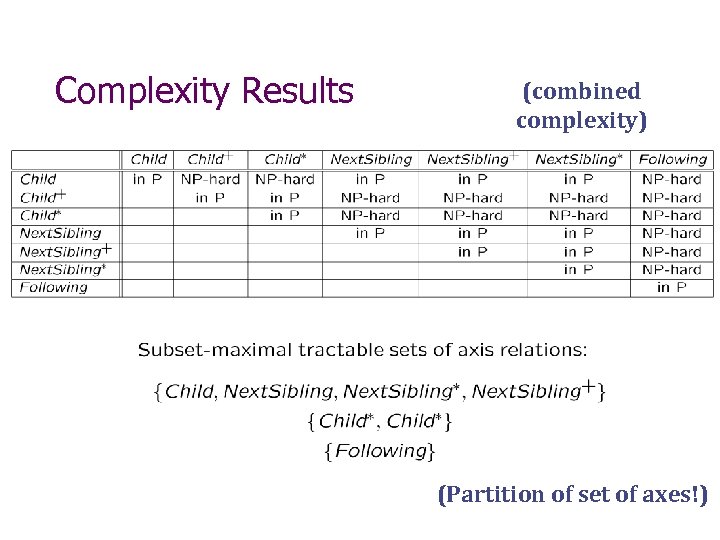
Complexity Results (combined complexity) (Partition of set of axes!)

Some simple tractability results: CQs with U-atoms and additional axe-sets {child} or {child+, child*} can be answered in time O(|data|*|query|). Proof idea for {child}: Cycles involving child: • unsatisfiable (easy to check), or • rewritable in linear time into acyclic CQs
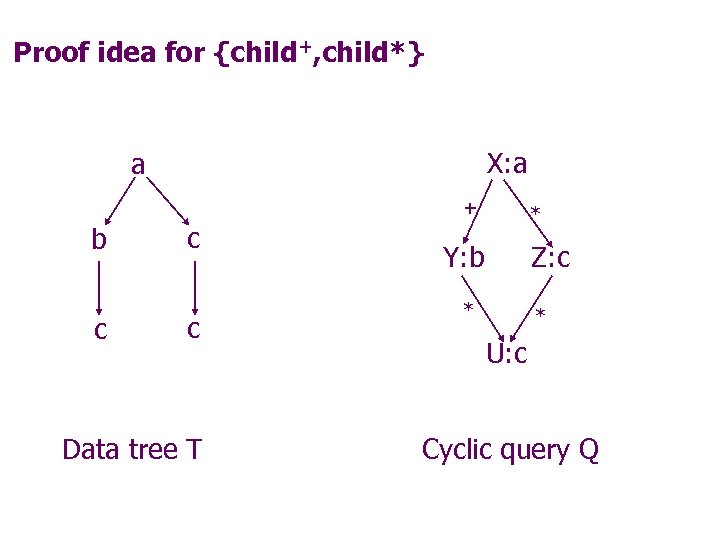
Proof idea for {child+, child*} X: a a + b c c c Data tree T * Y: b Z: c * * U: c Cyclic query Q
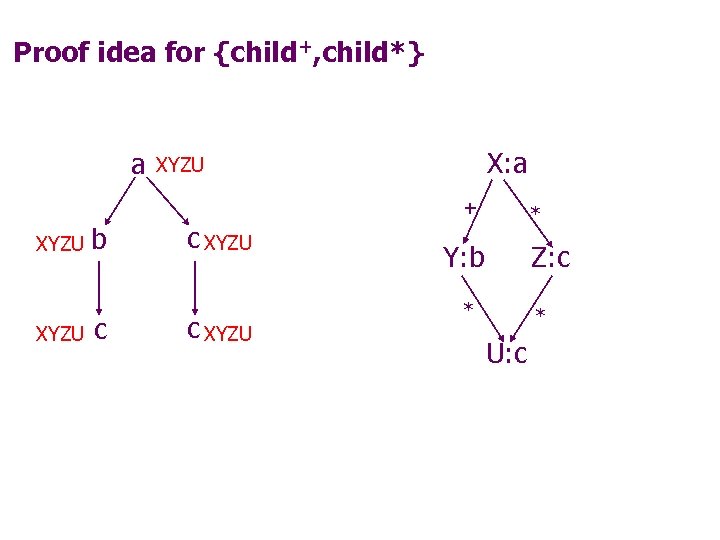
Proof idea for {child+, child*} a X: a XYZU + XYZU b c c XYZU * Y: b Z: c * * U: c
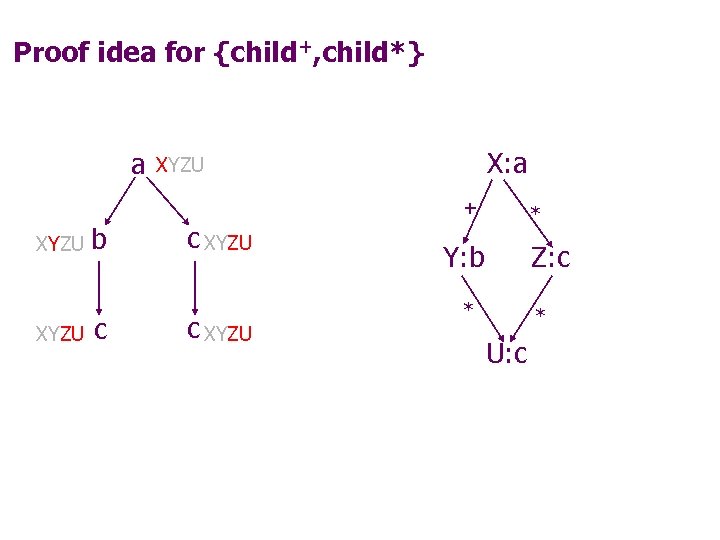
Proof idea for {child+, child*} a X: a XYZU + XYZU b c c XYZU * Y: b Z: c * * U: c
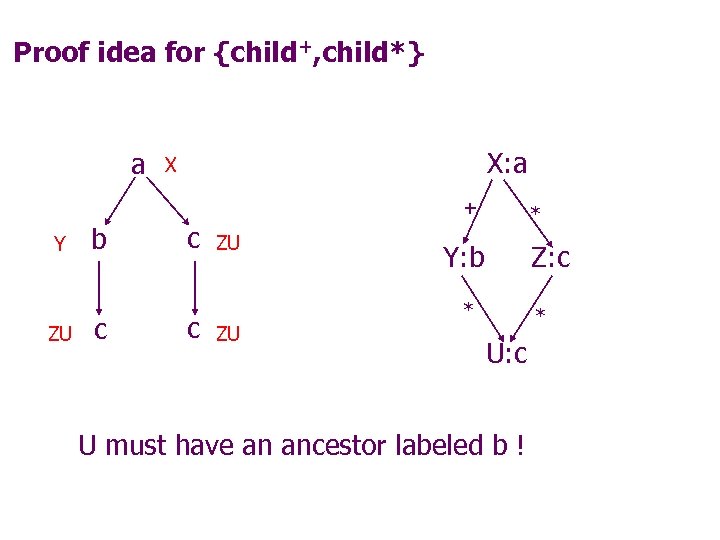
Proof idea for {child+, child*} a X: a X + Y ZU b c c c ZU ZU * Y: b Z: c * * U: c U must have an ancestor labeled b !
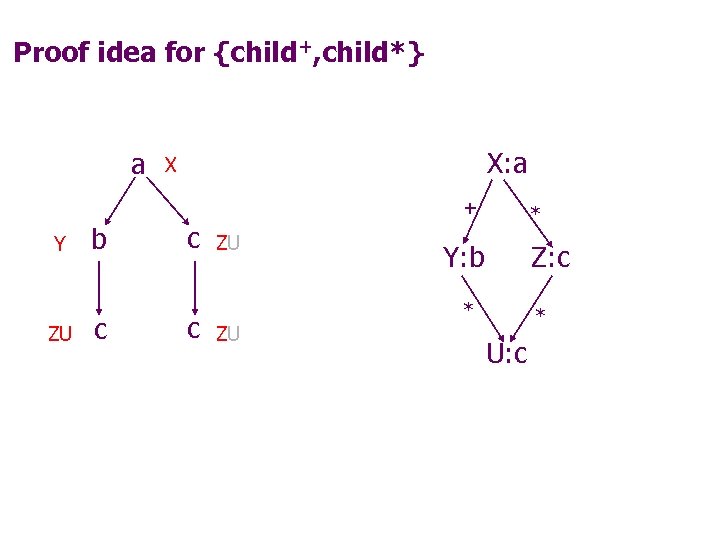
Proof idea for {child+, child*} a X: a X + Y ZU b c c c ZU ZU * Y: b Z: c * * U: c
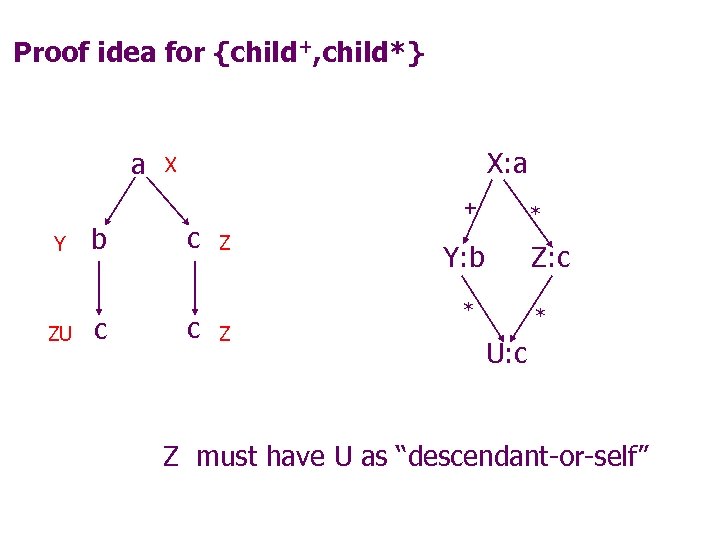
Proof idea for {child+, child*} a X: a X + Y ZU b c c c Z Z * Y: b Z: c * * U: c Z must have U as “descendant-or-self”
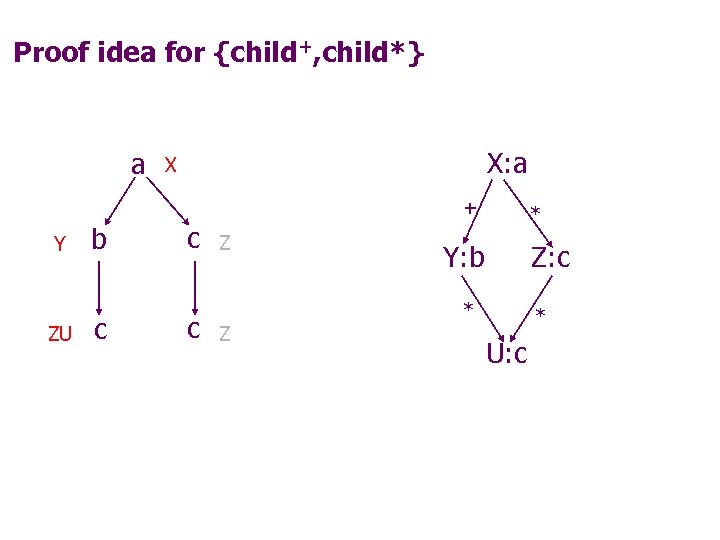
Proof idea for {child+, child*} a X: a X + Y ZU b c c c Z Z * Y: b Z: c * * U: c
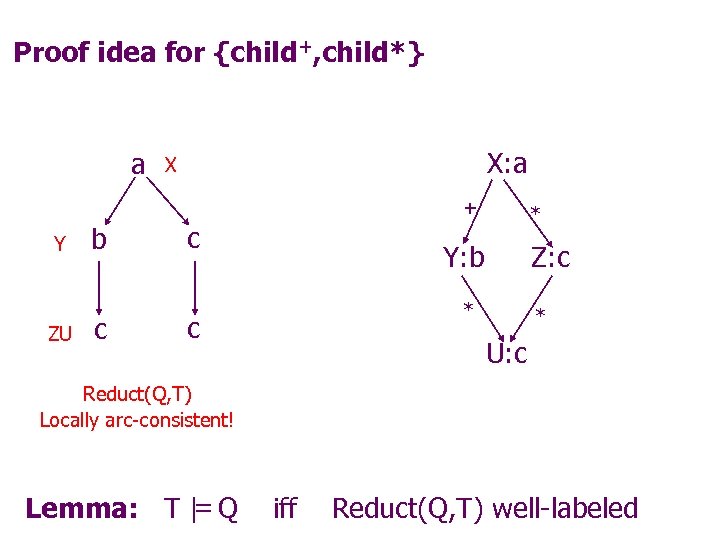
Proof idea for {child+, child*} a X: a X + Y ZU b c c * Y: b Z: c * U: c Reduct(Q, T) Locally arc-consistent! = Lemma: T | Q iff Reduct(Q, T) well-labeled
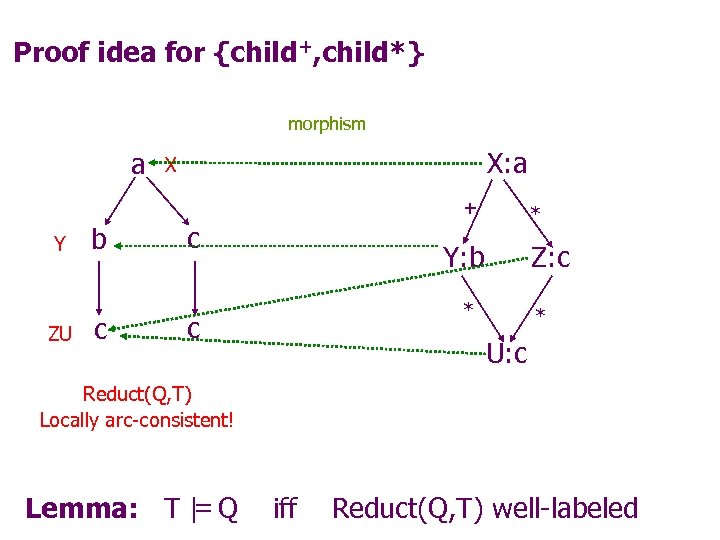
Proof idea for {child+, child*} morphism a X: a X + Y ZU b c c * Y: b Z: c * U: c Reduct(Q, T) Locally arc-consistent! = Lemma: T | Q iff Reduct(Q, T) well-labeled
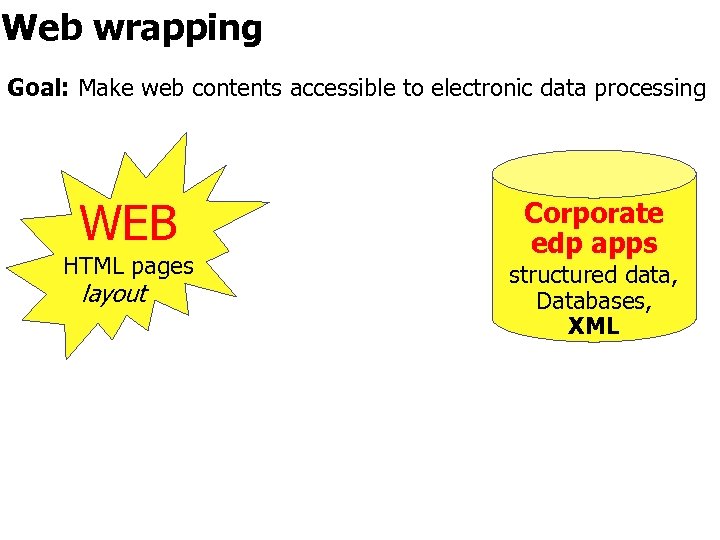
Web wrapping Goal: Make web contents accessible to electronic data processing WEB HTML pages layout Corporate edp apps structured data, Databases, XML
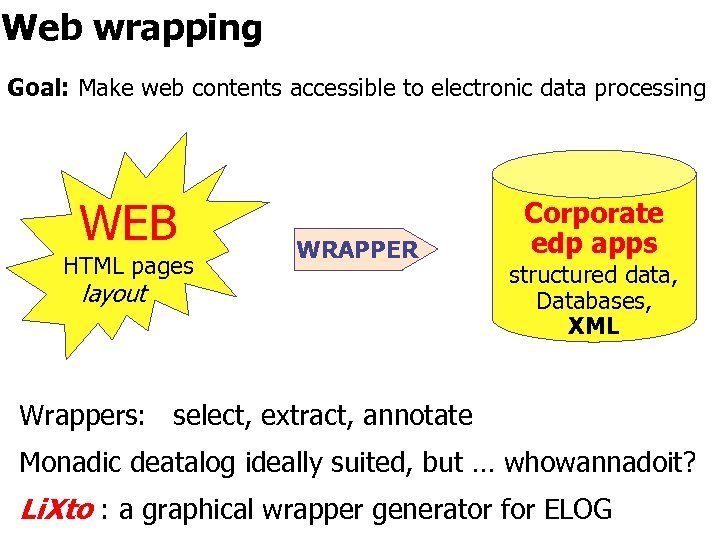
Web wrapping Goal: Make web contents accessible to electronic data processing WEB HTML pages WRAPPER layout Corporate edp apps structured data, Databases, XML Wrappers: select, extract, annotate Monadic deatalog ideally suited, but … whowannadoit? Li. Xto : a graphical wrapper generator for ELOG
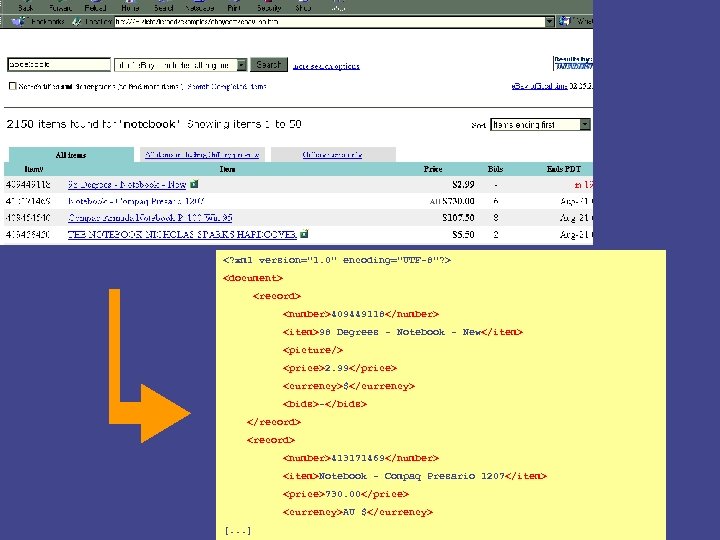
<? xml version="1. 0" encoding="UTF-8"? > <document> <record> <number>409449118</number> <item>98 Degrees - Notebook - New</item> <picture/> <price>2. 99</price> <currency>$</currency> <bids>-</bids> </record> <number>413171469</number> <item>Notebook - Compaq Presario 1207</item> <price>730. 00</price> <currency>AU $</currency> [. . . ]
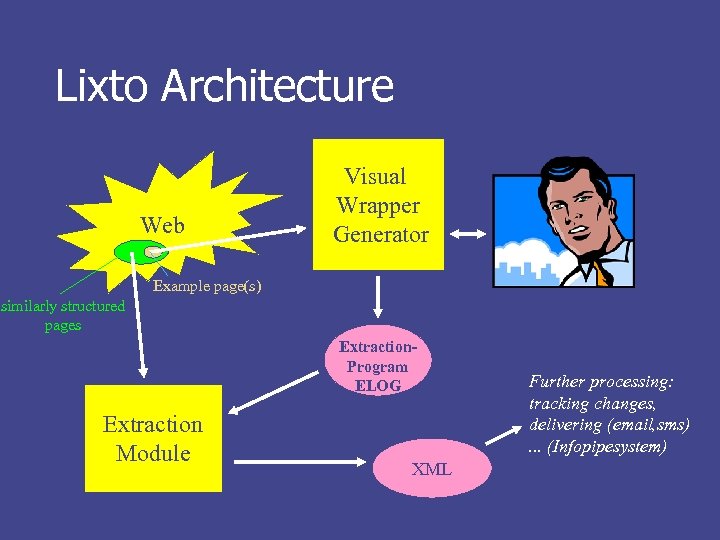
Lixto Architecture Web Visual Wrapper Generator Example page(s) similarly structured pages Extraction. Program ELOG Extraction Module XML Further processing: tracking changes, delivering (email, sms). . . (Infopipesystem)

Elog Program for e. Bay pages

Expressive power of Li. Xto Elog- : Monadic kernel of Elog Theorems [G. , Koch PODS 2002] ELOG- expresses monadic datalog All of ELOG- is graphically programmable via Li. Xto Corollary: Li. Xto expresses all MSO wrapping tasks.

Comparison to other Wrapper Generators Lixto more powerful than regular path queries Lixto more powerful than HEL (Sahuguet, Azavant) paper

The Lixto Suite • Automated navigation to target pages • Automated data extraction from target pages • Automated data analysis, transformation & integration • Automated data personalization • Automated data delivery Visual Wrapper Transformation Server
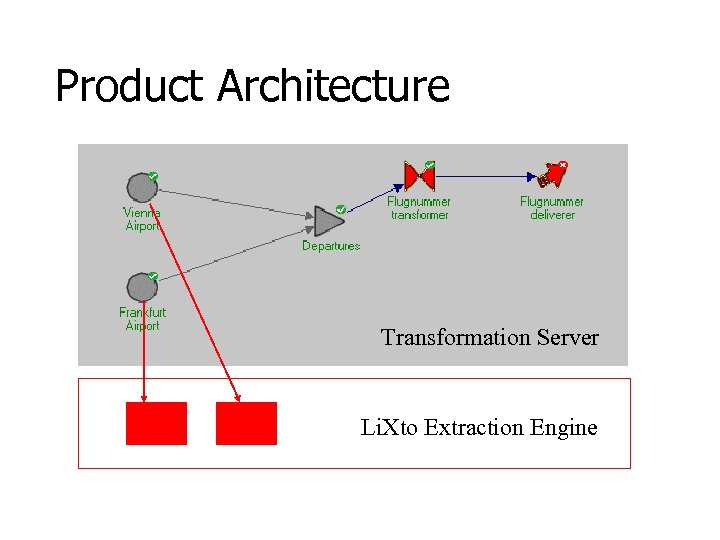
Product Architecture Transformation Server Li. Xto Extraction Engine
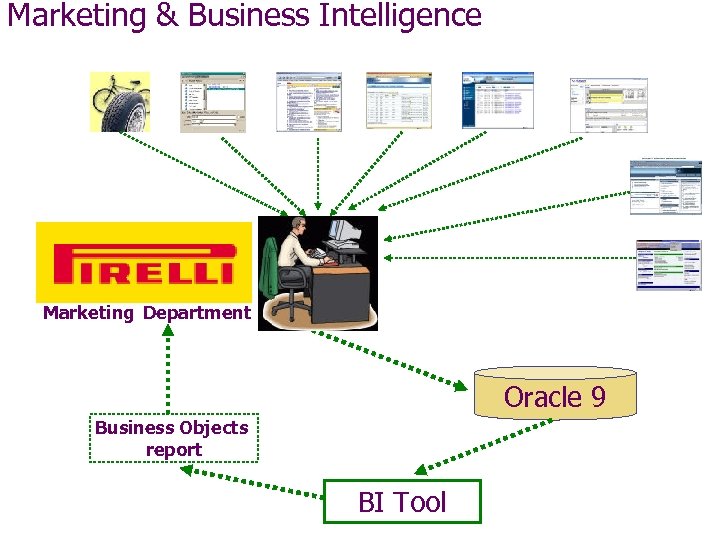
Marketing & Business Intelligence Marketing Department Oracle 9 Business Objects report BI Tool

Major Customers of Li. Xto:
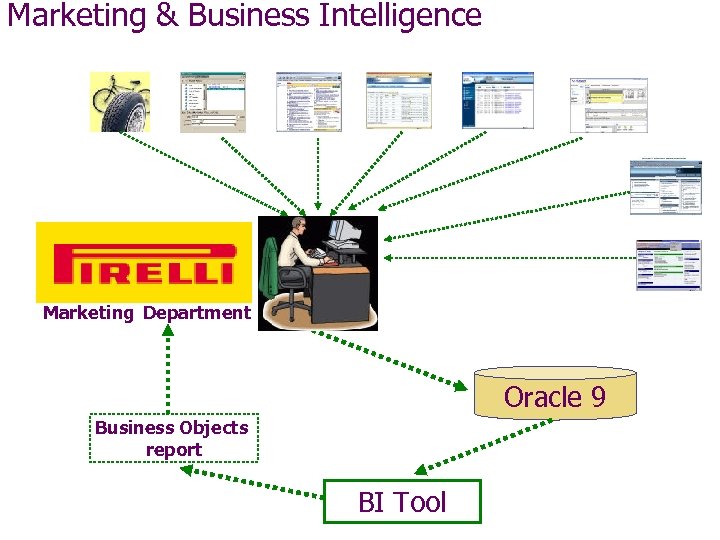
Marketing & Business Intelligence Marketing Department Oracle 9 Business Objects report BI Tool
c0c41c60948fd4f66f60d2d133df82af.ppt