Момент сили Умова рівноваги важеля Ще давні

Момент сили. Умова рівноваги важеля

Ще давні єгиптяни використали важіль і похилу, щоб підняти важкі кам’яні блоки до вершини піраміди.

Важіль — це твердий стрижень, що може обертатися навколо нерухомої опори. Причому цей стрижень обертається навколо нерухомої точки опори -віссю обертання.

Важіль — перший найпростіший механізм, яким людина користувалася протягом десятків тисяч років.

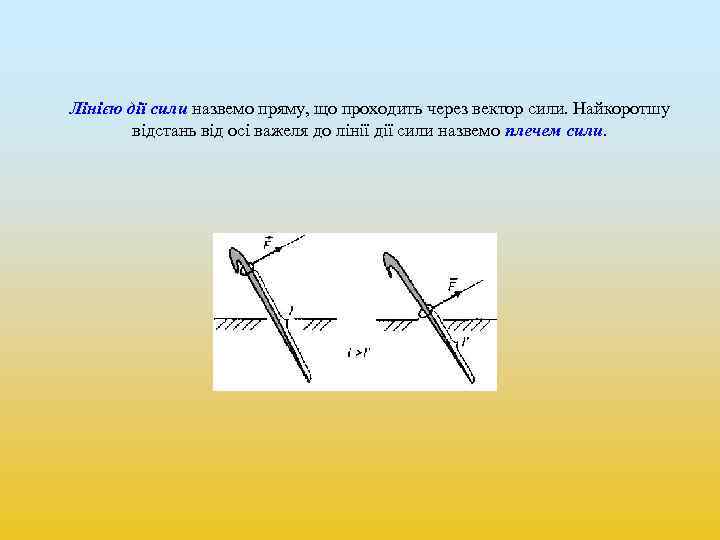Лінією дії сили назвемо пряму, що проходить через вектор сили. Найкоротшу відстань від осі важеля до лінії дії сили назвемо плечем сили.

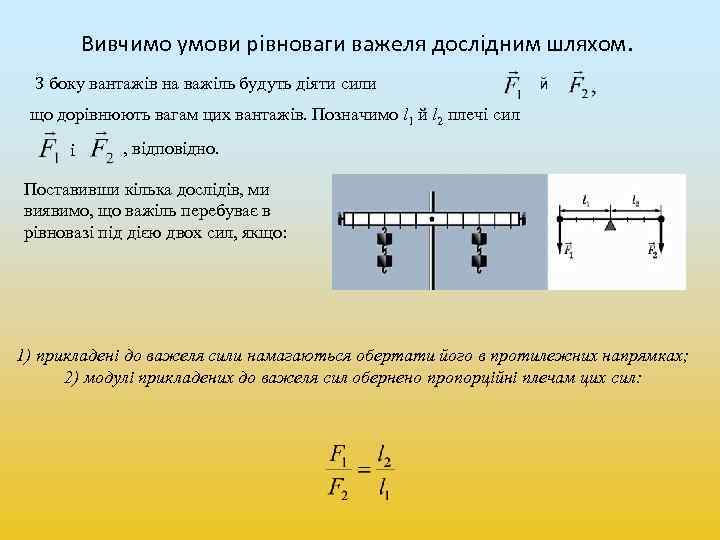Вивчимо умови рівноваги важеля дослідним шляхом. З боку вантажів на важіль будуть діяти сили й що дорівнюють вагам цих вантажів. Позначимо l 1 й l 2 плечі сил і , відповідно. Поставивши кілька дослідів, ми виявимо, що важіль перебуває в рівновазі під дією двох сил, якщо: 1) прикладені до важеля сили намагаються обертати його в протилежних напрямках; 2) модулі прикладених до важеля сил обернено пропорційні плечам цих сил:

в 1687 році французький учений П. Вариньон надав йому більш загальної форми, скориставшись поняттям моменту сили. Добуток модуля сили на її плече називають моментом сили. де M — момент сили, F — сила, l — плече сили.

Доведемо, що важіль перебуває в рівновазі, якщо момент сили, що обертає його за годинниковою стрілкою, дорівнює моменту сили, що обертає його проти годинникової стрілки, тобто Перетворимо вираз так, щоб у кожній частині рівності стояли величини, що характеризують тільки одну силу: її модуль і плече. Ми одержимо — момент сили, Але що намагається повернути важіль проти годинникової стрілки, а — момент сили, що намагається повернути важіль за годинниковою стрілкою.

Важіль перебуває в рівновазі, якщо сума моментів сил, що обертають важіль в одному напрямку, дорівнює сумі моментів сил, що обертають його в протилежному напрямку. Умову рівноваги в такому виді називають правилом моментів. Одиницею моменту сил є 1 H·м. Якщо ми одержуємо виграш у силі, то ми обов’язково програємо в переміщенні. Можна одержати виграш не тільки в силі, але й у переміщенні — прикладаючи силу до більш короткого плеча важеля. Правда, виграш у переміщенні неодмінно супроводжується програшем у силі.

Питання 1. Яке призначення простих механізмів? 2. Що таке лінія дії сили? 3. Як знайти плече сили? 4. Наведіть приклади використання умови рівноваги важеля. 5. Як можна за допомогою важеля одержати виграш у переміщенні? 6. Що характеризує момент сили?

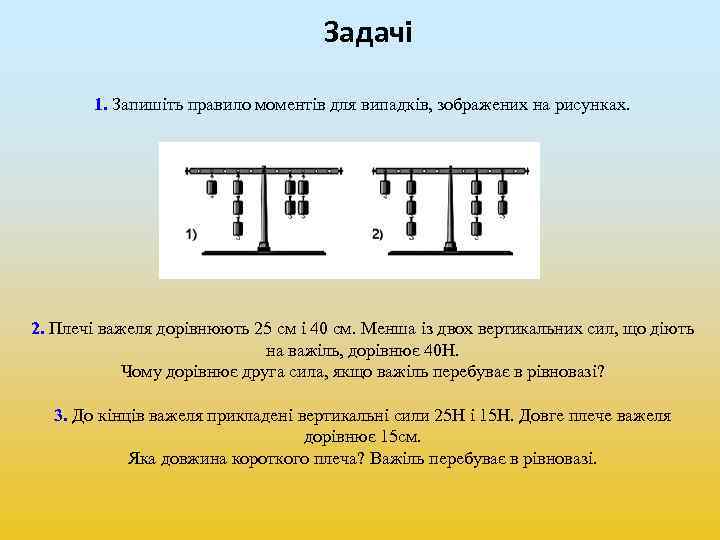Задачі 1. Запишіть правило моментів для випадків, зображених на рисунках. 2. Плечі важеля дорівнюють 25 см і 40 см. Менша із двох вертикальних сил, що діють на важіль, дорівнює 40 Н. Чому дорівнює друга сила, якщо важіль перебуває в рівновазі? 3. До кінців важеля прикладені вертикальні сили 25 Н і 15 Н. Довге плече важеля дорівнює 15 см. Яка довжина короткого плеча? Важіль перебуває в рівновазі.

Поміркуй 1. Чому ручку дверей розташовують ближче до краю? 2. Яке відношення довжин плечей важеля, що не дає ні виграшу, ні програшу в силі? У яких випадках є сенс застосовувати такий важіль?

Блоки. Похила площина

Блок, вісь якого закріплена й при підйомі вантажів не опускається й не піднімається, називають нерухомим блоком. Нерухомий блок можна розглядати як рівноплечий важіль, у якого плечі сил дорівнюють радіусу колеса: OA=OB=r. Умовою рівноваги блоку буде рівність прикладених сил: F=P Звідси випливає, що нерухомий блок не дає виграшу в силі, але дозволяє змінювати напрямок дії сили.

Рухомий блок — це блок, що піднімається й опускається разом з вантажем. Рухомий блок можна розглядати як важіль, що обертається навколо точки торкання мотузки й колеса (це точка О). Точка О — точка опори важеля, ОА — плече сили Р ОВ — плече сили F Оскільки плече ОВ вдвічі більше плеча ОА, то сила F вдвічі менше сили Р: Таким чином, рухомий блок дає виграш у силі у два рази.

Похила площина застосовується для переміщення важких предметів на більш високий рівень без їх безпосереднього підняття.

Якщо l — довжина похилої площини, h — висота похилої площини, P — вага візка, F — сила, прикладена до візка, то за відсутності сили тертя можна записати: При використанні похилої площини виграють у силі в стільки разів, у скільки разів довжина похилої площини більше її висоти.

Для всіх простих механізмів характерно наступне: користуючись ними, можна виграти або в силі (програвши у відстані), або у відстані (програвши в силі).

Питання 1. Наведіть приклади застосування нерухомого блоку. 2. Наведіть приклади застосування рухомого блоку. 3. Як за допомогою блоків одержати виграш у силі більше, ніж удвічі? 4. Якими простими механізмами ви користуєтеся в побуті? Наведіть приклади. 5. Чи можна розглядати нерухомий і рухомий блоки як важелі?

Задачі 1. Візок піднімають по похилій площині, прикладаючи силу 100 Н, спрямовану уздовж похилої площини. Яка маса візка, якщо довжина похилої площини 2 м, а висота 1 м? 2. Як за допомогою двох рухомих блоків одержати виграш у силі в 4 рази? Можна використати будь-яке число нерухомих блоків. Наведіть 2 розв’язки завдання.

Розв’язок 1) Можна використати 2 рухомих блоки й 1 нерухомий, як показано на лівому рисунку. Кожний з рухомих блоків дає виграш у силі в 2 рази, тому сила натягу мотузки a дорівнює 2 F, а сила натягу мотузки b, що втримує вантаж, дорівнює 4 F, тобто сумарний виграш у силі в 4 рази. 2) Можна використати 2 рухомих блоки й 2 нерухомих, як показано на правому рисунку. При цьому сила натягу кожної із двох мотузок, що утримують вантаж, дорівнює 2 F, завдяки чому виходить сумарний виграш у силі в 4 рази.

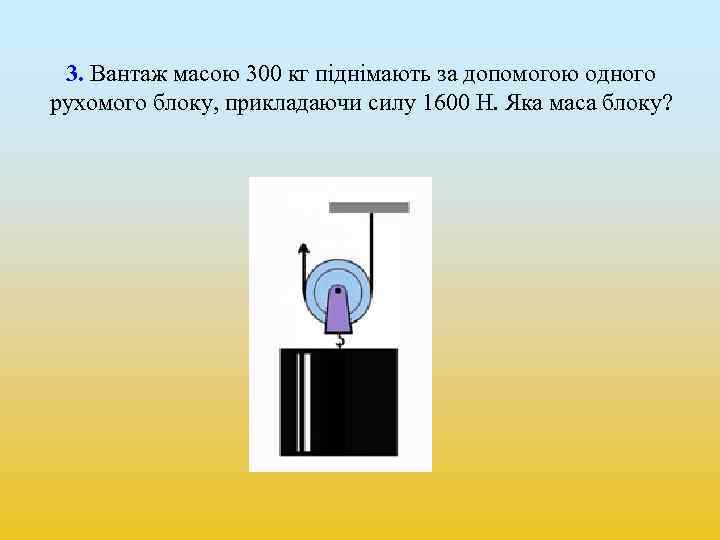3. Вантаж масою 300 кг піднімають за допомогою одного рухомого блоку, прикладаючи силу 1600 Н. Яка маса блоку?

Поміркуй 1. Чому діаметр ведучих коліс трактора значно більше діаметра ведучих коліс легкового автомобіля? 2. Чому розмотувати нитку з повної котушки легше, ніж із частково розмотаної? 3. Як можна з’єднати один з одним нерухомі й рухомі блоки, щоб одержати виграш у силі в 6 разів? 4. У якому напрямку треба тягти вільний кінець мотузки, щоб легше було піднімати вантаж?