es_statics_lecture_3_2013.ppt
- Количество слайдов: 18
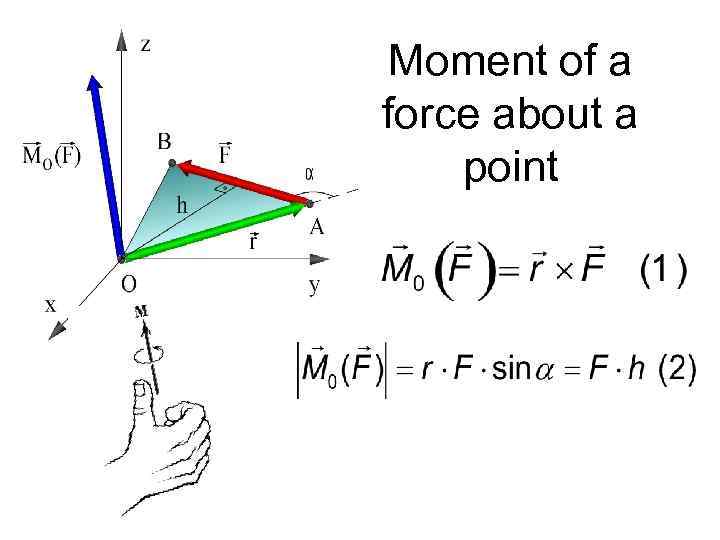
Moment of a force about a point

The moment of a force about a center (point) is a vector whose magnitude is determined as a product of the force magnitude and its arm. The arm is the shortest distance (perpendicular) between the center and the force’s line of action. The vector of moment is perpendicular to the plane of the force and position vector and is directed so that the shortest rotation is counterclockwise when viewed from the end of the vector.

• The projection of the moment about the point onto an axis that passes through the point is called the moment of force about the axis

Moments of a force about the coordinate axes • Moment of a force about the axis Ox • Moment of a force about the axis Oy • Moment of a force about the axis Oz
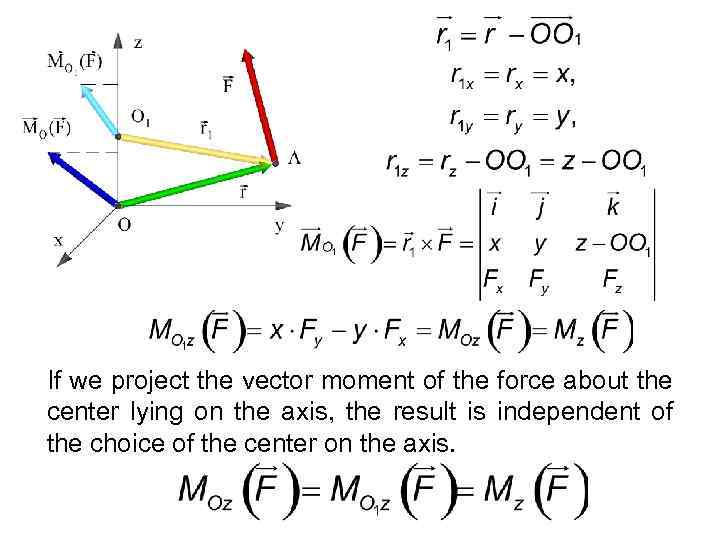
If we project the vector moment of the force about the center lying on the axis, the result is independent of the choice of the center on the axis.
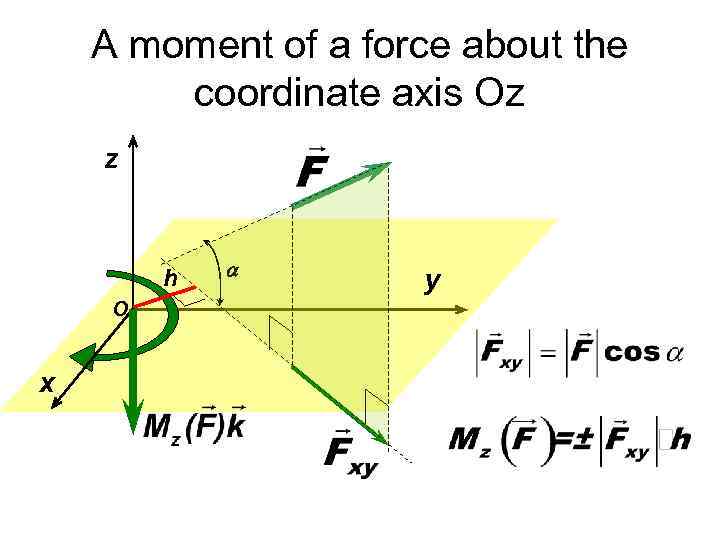
A moment of a force about the coordinate axis Oz z h O x y

The moment of the force about the axis can be obtained in the following steps: 1. Project the force onto plane that is perpendicular to axis. 2. Determine the arm h of the force projection with respect to the point of intersection of the axis and plane. 3. Calculate the moment of the force about the axis as a positive or negative product of the magnitude of the force projection and its arm.

The moment of force about the axis is equal to zero if the force and axis lie in the same plane: –the force is parallel to the axis, –the line of force action intersects the axis.
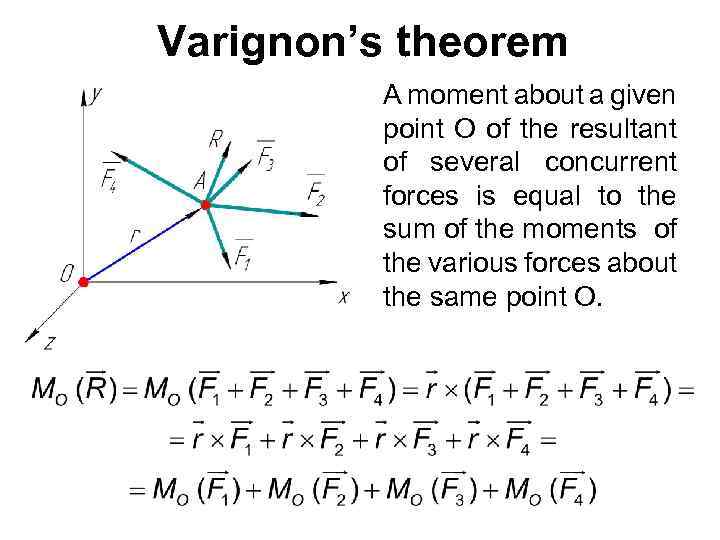
Varignon’s theorem A moment about a given point O of the resultant of several concurrent forces is equal to the sum of the moments of the various forces about the same point O.
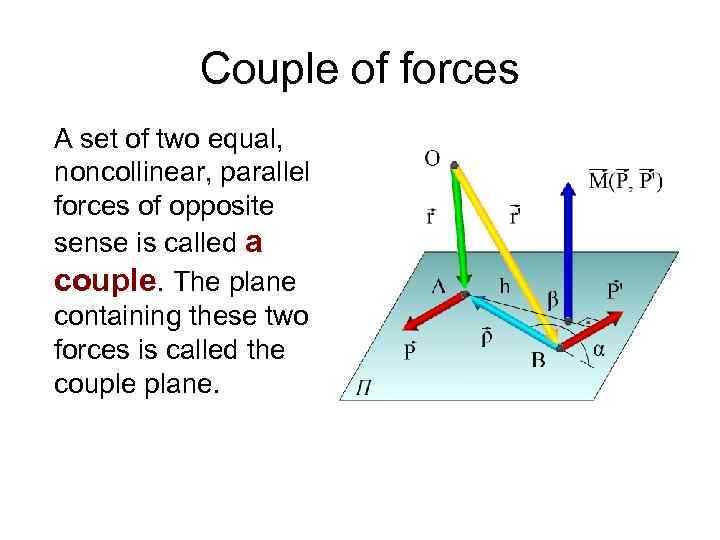
Couple of forces A set of two equal, noncollinear, parallel forces of opposite sense is called a couple. The plane containing these two forces is called the couple plane.


The couple vector moment is free vector which can be applied at any point without changing its magnitude and direction

Couple features (theorems) • Couple characteristics (arm, magnitude of the force) can be changed provided the couple moment remains constant. • An effect of a couple on the rigid body will remain unchanged if the couple is translated (is shifted by parallel translation). • An effect of a couple on the rigid body will remain unchanged if the couple is revolved an orbit angle in couple plane.

The couple features consequences • Consequence 1. Two couples applied to a rigid body and having the same vector moment are equivalent.
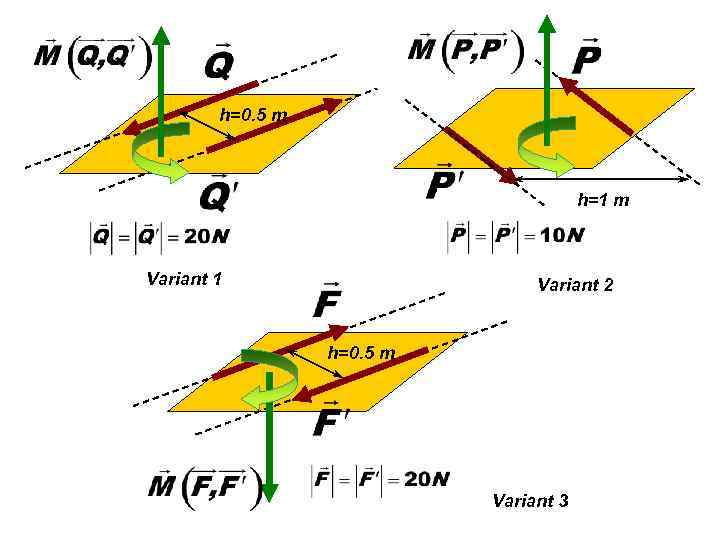
h=0. 5 m h=1 m Variant 1 Variant 2 h=0. 5 m Variant 3

• Consequence 2. Two couples applied to a rigid body may be replaced by a single couple with vector moment equal to the sum of vector moments of the two original couples.
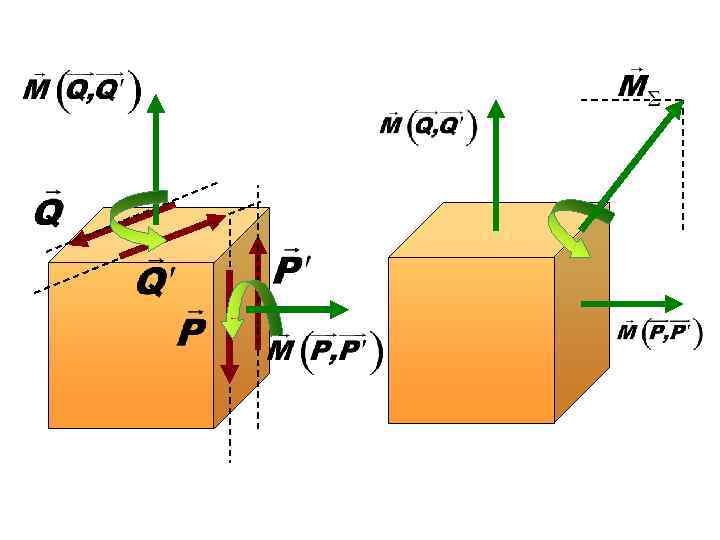

The first problem of statics – system equivalence: a system of n couples applied to a rigid body is equivalent to a single couple with vector moment equal to the geometrical sum of original couples vector moments The second problem of statics – conditions of equilibrium: a system of n couples applied to a rigid body is balanced if a single couple to which the original system may be reduced is equivalent to zero.
es_statics_lecture_3_2013.ppt