МОДУЛЬ 3 МКТ 2009.ppt
- Количество слайдов: 46
 МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ. ОСНОВЫ ТЕРМОДИНАМИКИ Законы состояния идеального газа • • давление идеального газа; уравнение Менделеева-Клапейрона, газовые законы; понятие о степенях свободы; внутренняя энергия идеального газа; распределение Максвелла по скоростям и энергии; распределение Больцмана; поток газа на стенку Агрегатное состояние вещества • • • реальные газы; уравнение Ван-дер. Ваальса; критические параметры; фазовые переходы Явления переноса • • критерии вакуума; столкновения; теплопроводность; внутреннее трение; диффузия. Термодинамика • • процессы изменения состояния газа; работа; I начало термодинамики; теплоемкость; политропические процессы; циклические процессы и их КПД; II начало термодинамики; энтропия; III начало термодинамики
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ. ОСНОВЫ ТЕРМОДИНАМИКИ Законы состояния идеального газа • • давление идеального газа; уравнение Менделеева-Клапейрона, газовые законы; понятие о степенях свободы; внутренняя энергия идеального газа; распределение Максвелла по скоростям и энергии; распределение Больцмана; поток газа на стенку Агрегатное состояние вещества • • • реальные газы; уравнение Ван-дер. Ваальса; критические параметры; фазовые переходы Явления переноса • • критерии вакуума; столкновения; теплопроводность; внутреннее трение; диффузия. Термодинамика • • процессы изменения состояния газа; работа; I начало термодинамики; теплоемкость; политропические процессы; циклические процессы и их КПД; II начало термодинамики; энтропия; III начало термодинамики
 ОСНОВНЫЕ ПОНЯТИЯ Термодинамический которых Молекулярная физика — это Статистический метод и термодинамика — разделы физики, вметод — это метод исследования систем из изучаются зависимости свойств метод исследования систем из тел от их строения, взаимодействия между большого числа частицами, из которых состоят тела, и характера движения частиц, оперирующий большого числа частиц, величинами, характеризующими оперирующий статистическими систему в целом (например, давление, закономерностями и средними объем, температура) при различных (усредненными) значениями превращениях энергии, происходящих в физических величин, системе, не учитывая при этом характеризующих всю систему. внутреннего строения изучаемых тел и характера движения отдельных частиц. молекулярная физика — раздел физики, изучающего строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из атомов, молекул или ионов находящихся в непрерывном хаотическом движении. . термодинамика — раздела физики, изучающего общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.
ОСНОВНЫЕ ПОНЯТИЯ Термодинамический которых Молекулярная физика — это Статистический метод и термодинамика — разделы физики, вметод — это метод исследования систем из изучаются зависимости свойств метод исследования систем из тел от их строения, взаимодействия между большого числа частицами, из которых состоят тела, и характера движения частиц, оперирующий большого числа частиц, величинами, характеризующими оперирующий статистическими систему в целом (например, давление, закономерностями и средними объем, температура) при различных (усредненными) значениями превращениях энергии, происходящих в физических величин, системе, не учитывая при этом характеризующих всю систему. внутреннего строения изучаемых тел и характера движения отдельных частиц. молекулярная физика — раздел физики, изучающего строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из атомов, молекул или ионов находящихся в непрерывном хаотическом движении. . термодинамика — раздела физики, изучающего общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.
 ОСНОВНЫЕ ПОНЯТИЯ термодинамическая система — совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Термодинамические системы, не обменивающиеся с внешней средой ни энергией, ни веществом, называются замкнутыми. Если для данной системы внешние условия не изменяются и состояние системы с течением времени не меняется, то эта система находится в термодинамическом равновесии. Состояние системы задается термодинамическими параметрами (параметрами состояния) — совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и объем. Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом.
ОСНОВНЫЕ ПОНЯТИЯ термодинамическая система — совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Термодинамические системы, не обменивающиеся с внешней средой ни энергией, ни веществом, называются замкнутыми. Если для данной системы внешние условия не изменяются и состояние системы с течением времени не меняется, то эта система находится в термодинамическом равновесии. Состояние системы задается термодинамическими параметрами (параметрами состояния) — совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и объем. Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом.
 ОСНОВНЫЕ ПОНЯТИЯ Температура — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы и определяющая направление теплообмена между телами. Термодинамическая температурная шкала (шкала Кельвина), градуированная в градусах Кельвина (К) определяется по одной реперной точке — тройной точке воды — температуре, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии. Температура этой точки по данной шкале равна 273, 16 К. Международная практическая шкала (шкала Цельсия ) градуированная в градусах Цельсия (°С) по двум реперным точкам — температурам замерзания и кипения воды при давлении 1, 013· 105 Па, которые принимаются соответственно 0°С и 100°С
ОСНОВНЫЕ ПОНЯТИЯ Температура — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы и определяющая направление теплообмена между телами. Термодинамическая температурная шкала (шкала Кельвина), градуированная в градусах Кельвина (К) определяется по одной реперной точке — тройной точке воды — температуре, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии. Температура этой точки по данной шкале равна 273, 16 К. Международная практическая шкала (шкала Цельсия ) градуированная в градусах Цельсия (°С) по двум реперным точкам — температурам замерзания и кипения воды при давлении 1, 013· 105 Па, которые принимаются соответственно 0°С и 100°С
 ОСНОВНЫЕ ПОНЯТИЯ Температура — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы и определяющая направление теплообмена между телами. Термодинамическая температурная шкала (шкала Кельвина), градуированная в градусах Кельвина (К) определяется по одной реперной точке — тройной точке воды — температуре, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии. Температура этой точки по данной шкале равна 273, 16 К. Международная практическая шкала (шкала Цельсия ) градуированная в градусах Цельсия (°С) по двум реперным точкам — температурам замерзания и кипения воды при давлении 1, 013· 105 Па, которые принимаются соответственно 0°С и 100°С Физическая модель, идеального газа 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутствуют силы взаимодействия; взаимодействия 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие
ОСНОВНЫЕ ПОНЯТИЯ Температура — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы и определяющая направление теплообмена между телами. Термодинамическая температурная шкала (шкала Кельвина), градуированная в градусах Кельвина (К) определяется по одной реперной точке — тройной точке воды — температуре, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии. Температура этой точки по данной шкале равна 273, 16 К. Международная практическая шкала (шкала Цельсия ) градуированная в градусах Цельсия (°С) по двум реперным точкам — температурам замерзания и кипения воды при давлении 1, 013· 105 Па, которые принимаются соответственно 0°С и 100°С Физическая модель, идеального газа 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутствуют силы взаимодействия; взаимодействия 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие
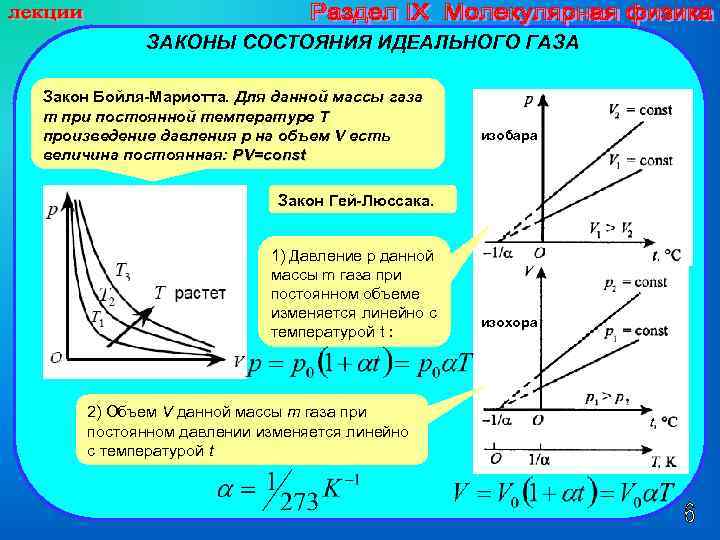 ЗАКОНЫ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА Закон Бойля-Мариотта. Для данной массы газа m при постоянной температуре T произведение давления p на объем V есть величина постоянная: PV=const изобара Закон Гей-Люссака. 1) Давление p данной массы m газа при постоянном объеме изменяется линейно с температурой t : 2) Объем V данной массы m газа при постоянном давлении изменяется линейно с температурой t изохора
ЗАКОНЫ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА Закон Бойля-Мариотта. Для данной массы газа m при постоянной температуре T произведение давления p на объем V есть величина постоянная: PV=const изобара Закон Гей-Люссака. 1) Давление p данной массы m газа при постоянном объеме изменяется линейно с температурой t : 2) Объем V данной массы m газа при постоянном давлении изменяется линейно с температурой t изохора
 ЗАКОНЫ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА Закон Авогадро: моли любых газов при одинаковой температуре и давлении занимают одинаковые объемы. В одном моле различных веществ содержится одно и то же число молекул NA, называемое числом Авогадро. Количество вещества ν— число специфических структурных элементов — молекул, атомов или ионов, из которых состоит вещество. моль — количество вещества системы, содержащей столько же структурных элементов, сколько содержится в 0, 012 кг изотопа углерода 12 С. Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений n входящих в нее газов: Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре При нормальных условиях (T = T 0 , p = p 0 ) этот объем Vµ (молярный объем) равен
ЗАКОНЫ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА Закон Авогадро: моли любых газов при одинаковой температуре и давлении занимают одинаковые объемы. В одном моле различных веществ содержится одно и то же число молекул NA, называемое числом Авогадро. Количество вещества ν— число специфических структурных элементов — молекул, атомов или ионов, из которых состоит вещество. моль — количество вещества системы, содержащей столько же структурных элементов, сколько содержится в 0, 012 кг изотопа углерода 12 С. Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений n входящих в нее газов: Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре При нормальных условиях (T = T 0 , p = p 0 ) этот объем Vµ (молярный объем) равен
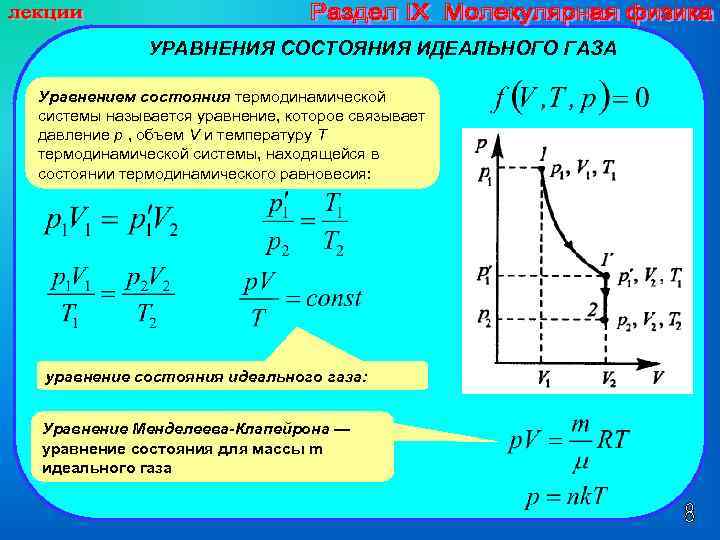 УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА Уравнением состояния термодинамической системы называется уравнение, которое связывает давление p , объем V и температуру T термодинамической системы, находящейся в состоянии термодинамического равновесия: уравнение состояния идеального газа: Уравнение Менделеева-Клапейрона — уравнение состояния для массы m идеального газа
УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА Уравнением состояния термодинамической системы называется уравнение, которое связывает давление p , объем V и температуру T термодинамической системы, находящейся в состоянии термодинамического равновесия: уравнение состояния идеального газа: Уравнение Менделеева-Клапейрона — уравнение состояния для массы m идеального газа
 РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА Средняя скорость молекулы газа Наиболее вероятная скорость молекул идеального газа. В газе, находящемся в состоянии равновесия при данной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям. Это распределение описывается функцией f (v), называемой функцией распределения молекул по скоростям
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА Средняя скорость молекулы газа Наиболее вероятная скорость молекул идеального газа. В газе, находящемся в состоянии равновесия при данной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям. Это распределение описывается функцией f (v), называемой функцией распределения молекул по скоростям
 РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА Давление на высоте h газа с молярной массой µ относительно уровня моря, где давление p 0 считается нормальным При постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Такое распределение называют распределением Больцмана (распределение частиц по значениям потенциальной энергии) для внешнего потенциального поля. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле,
РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА Давление на высоте h газа с молярной массой µ относительно уровня моря, где давление p 0 считается нормальным При постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Такое распределение называют распределением Больцмана (распределение частиц по значениям потенциальной энергии) для внешнего потенциального поля. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле,
 ПОТОК ЧАСТИЦ НА СТЕНКУ
ПОТОК ЧАСТИЦ НА СТЕНКУ
 ПОТОК ЭНЕРГИИ, ПЕРЕНОСИМОЙ ЧАСТИЦАМИ НА СТЕНКУ
ПОТОК ЭНЕРГИИ, ПЕРЕНОСИМОЙ ЧАСТИЦАМИ НА СТЕНКУ
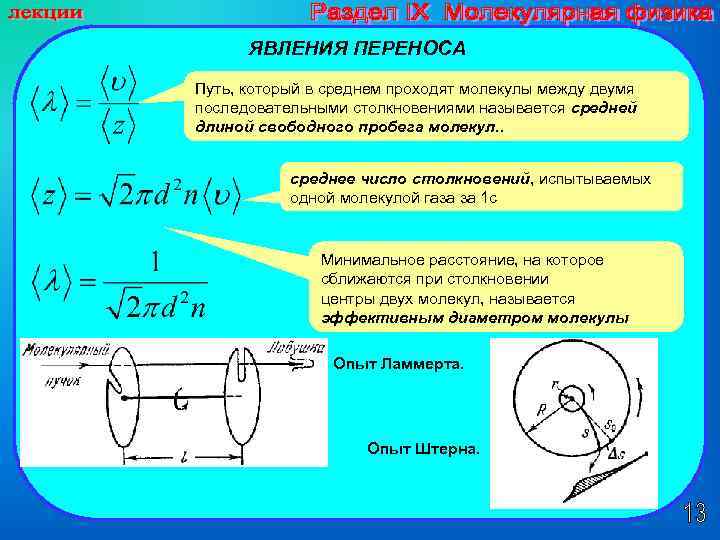 ЯВЛЕНИЯ ПЕРЕНОСА Путь, который в среднем проходят молекулы между двумя последовательными столкновениями называется средней длиной свободного пробега молекул. . среднее число столкновений, испытываемых одной молекулой газа за 1 с Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы Опыт Ламмерта. Опыт Штерна.
ЯВЛЕНИЯ ПЕРЕНОСА Путь, который в среднем проходят молекулы между двумя последовательными столкновениями называется средней длиной свободного пробега молекул. . среднее число столкновений, испытываемых одной молекулой газа за 1 с Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы Опыт Ламмерта. Опыт Штерна.
 ЯВЛЕНИЯ ПЕРЕНОСА Явлениями переноса называются необратимые процессы в термодинамически неравновесных системах, в которых происходит пространственный перенос энергии теплопроводность), массы (диффузия), импульса (внутреннее трение). Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул — выравнивание температур Коэффициент теплопроводности Перенос энергии (в форме теплоты) описывается законом Фурье: Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену частицами (перенос масс) между этими телами, возникает и продолжается, пока существует градиент плотности.
ЯВЛЕНИЯ ПЕРЕНОСА Явлениями переноса называются необратимые процессы в термодинамически неравновесных системах, в которых происходит пространственный перенос энергии теплопроводность), массы (диффузия), импульса (внутреннее трение). Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул — выравнивание температур Коэффициент теплопроводности Перенос энергии (в форме теплоты) описывается законом Фурье: Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену частицами (перенос масс) между этими телами, возникает и продолжается, пока существует градиент плотности.
 ЯВЛЕНИЯ ПЕРЕНОСА Перенос массы (диффузия) для химически однородного газа подчиняется закону Фика: Коэффициент диффузии Внутреннее трение (вязкость). Вследствие хаотического теплового движения молекул происходит обмен молекулами между слоями газа движущимися с различными скоростями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее — увеличивается (происходит перенос импульса от одного слоя к другому). Это приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. . Внутреннее трение описывается законом Ньютона: Коэффициент вязкости Формулы для коэффициентов λ, D и η связывают коэффициенты переноса и характеристики теплового движения молекул.
ЯВЛЕНИЯ ПЕРЕНОСА Перенос массы (диффузия) для химически однородного газа подчиняется закону Фика: Коэффициент диффузии Внутреннее трение (вязкость). Вследствие хаотического теплового движения молекул происходит обмен молекулами между слоями газа движущимися с различными скоростями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее — увеличивается (происходит перенос импульса от одного слоя к другому). Это приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. . Внутреннее трение описывается законом Ньютона: Коэффициент вязкости Формулы для коэффициентов λ, D и η связывают коэффициенты переноса и характеристики теплового движения молекул.
 ТЕРМОДИНАМИКА Внутренняя энергия U — это энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д. ) и энергия взаимодействия этих частиц. • • • кинетическая энергия хаотического движения молекул; энергия взаимодействия атомов и молекул между собой и с ядрами атомов; энергия взаимодействия электронов между собой и с ядрами; энергия движения и взаимодействия нуклонов в ядре; к ней не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях. Работа и количество теплоты – энергетические характеристики термодинамического процесса, обуславливающего переход из одного состояния в другое Передача внешними телами энергии в форме работы сопровождается макроскопическим перемещением внешних тел Количество энергии, передаваемой системе внешними телами в форме теплоты, называется количеством теплоты или теплотой Q сообщаемой передаваемой системе
ТЕРМОДИНАМИКА Внутренняя энергия U — это энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д. ) и энергия взаимодействия этих частиц. • • • кинетическая энергия хаотического движения молекул; энергия взаимодействия атомов и молекул между собой и с ядрами атомов; энергия взаимодействия электронов между собой и с ядрами; энергия движения и взаимодействия нуклонов в ядре; к ней не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях. Работа и количество теплоты – энергетические характеристики термодинамического процесса, обуславливающего переход из одного состояния в другое Передача внешними телами энергии в форме работы сопровождается макроскопическим перемещением внешних тел Количество энергии, передаваемой системе внешними телами в форме теплоты, называется количеством теплоты или теплотой Q сообщаемой передаваемой системе
 ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ Первое начало термодинамики – это закон сохранения и превращения энергии в термодинамических процессах. вечный двигатель первого рода — периодически действующий двигатель, который совершал бы бóльшую работу, чем сообщенная ему извне энергия, — невозможен. Равновесные процессы — это процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. При неравновесных процессах значения параметров в разных частях системы различны и не существует, (p V ) -точек, характеризующих состояние всей системы. Поэтому графическое изображение неравновесного процесса невозможно. Все реальные процессы неравновесны, но в ряде случаев (достаточно медленные процессы) неравновесностью реальных процессов можно пренебречь.
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ Первое начало термодинамики – это закон сохранения и превращения энергии в термодинамических процессах. вечный двигатель первого рода — периодически действующий двигатель, который совершал бы бóльшую работу, чем сообщенная ему извне энергия, — невозможен. Равновесные процессы — это процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. При неравновесных процессах значения параметров в разных частях системы различны и не существует, (p V ) -точек, характеризующих состояние всей системы. Поэтому графическое изображение неравновесного процесса невозможно. Все реальные процессы неравновесны, но в ряде случаев (достаточно медленные процессы) неравновесностью реальных процессов можно пренебречь.
 ТЕПЛОЕМКОСТЬ Удельная теплоемкость вещества c — величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К. Единица удельной теплоемкости — Дж/(кг К) Молярная теплоемкость C — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К. Единица молярной теплоемкости — Дж/(моль К). Молярные теплоемкости Формула Майера
ТЕПЛОЕМКОСТЬ Удельная теплоемкость вещества c — величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К. Единица удельной теплоемкости — Дж/(кг К) Молярная теплоемкость C — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К. Единица молярной теплоемкости — Дж/(моль К). Молярные теплоемкости Формула Майера
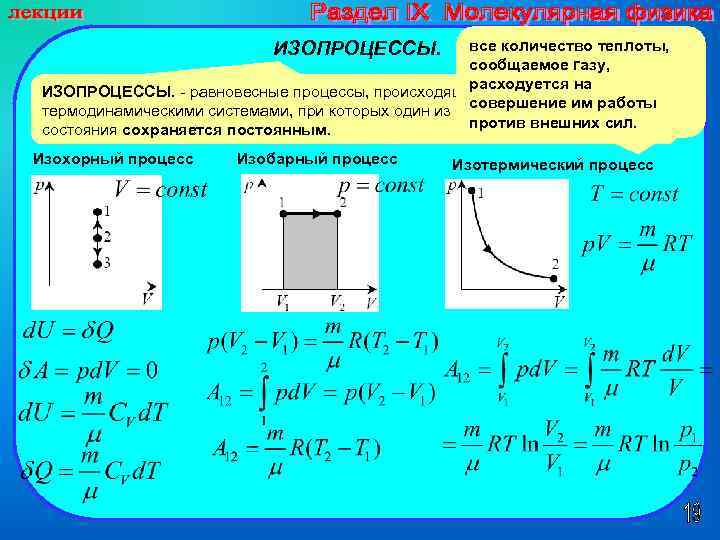 все количество теплоты, сообщаемое газу, расходуется на ИЗОПРОЦЕССЫ. - равновесные процессы, происходящие с совершение им работы термодинамическими системами, при которых один из основных параметров против внешних сил. состояния сохраняется постоянным. ИЗОПРОЦЕССЫ. Изохорный процесс Изобарный процесс Изотермический процесс
все количество теплоты, сообщаемое газу, расходуется на ИЗОПРОЦЕССЫ. - равновесные процессы, происходящие с совершение им работы термодинамическими системами, при которых один из основных параметров против внешних сил. состояния сохраняется постоянным. ИЗОПРОЦЕССЫ. Изохорный процесс Изобарный процесс Изотермический процесс
 ИЗОПРОЦЕССЫ. Адиабатический процесс Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (δQ = 0 ) К адиабатическим процессам можно отнести все быстропротекающие процессы (теплообмен не успевает совершиться), например, распространение звука в среде, циклы расширения и сжатия в двигателях внутреннего сгорания, в холодильных установках и т. д. Коэффициент Пуассона
ИЗОПРОЦЕССЫ. Адиабатический процесс Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (δQ = 0 ) К адиабатическим процессам можно отнести все быстропротекающие процессы (теплообмен не успевает совершиться), например, распространение звука в среде, циклы расширения и сжатия в двигателях внутреннего сгорания, в холодильных установках и т. д. Коэффициент Пуассона
 ИЗОПРОЦЕССЫ. Адиабатический процесс Работа при адиабатном расширении меньше чем при изотермическом Уравнения Пуассона при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
ИЗОПРОЦЕССЫ. Адиабатический процесс Работа при адиабатном расширении меньше чем при изотермическом Уравнения Пуассона при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
 ПОЛИТРОПИЧЕСКИЕ ПРОЦЕССЫ Процесс, в котором теплоемкость остается постоянной называется политропическим. Рассмотренные выше изохорный, изотермический, изобарный и адиабатический процессы — это частные случаи политропного процесса. показатель политропы Уравнение политропы
ПОЛИТРОПИЧЕСКИЕ ПРОЦЕССЫ Процесс, в котором теплоемкость остается постоянной называется политропическим. Рассмотренные выше изохорный, изотермический, изобарный и адиабатический процессы — это частные случаи политропного процесса. показатель политропы Уравнение политропы
 ОБРАТИМЫЙ И НЕОБРАТИМЫЙ ПРОЦЕССЫ. ЦИКЛЫ. Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении. Причем, если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым. Реальные процессы необратимы, в них всегда происходит диссипация (потеря) энергии (из-за трения, теплопроводности и т. д. ). Обратимые процессы — это физическая модель —идеализация реальных процессов. Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние. Работа за цикл A определяется площадью, охватываемой замкнутой кривой:
ОБРАТИМЫЙ И НЕОБРАТИМЫЙ ПРОЦЕССЫ. ЦИКЛЫ. Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении. Причем, если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым. Реальные процессы необратимы, в них всегда происходит диссипация (потеря) энергии (из-за трения, теплопроводности и т. д. ). Обратимые процессы — это физическая модель —идеализация реальных процессов. Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние. Работа за цикл A определяется площадью, охватываемой замкнутой кривой:
 ОБРАТИМЫЙ И НЕОБРАТИМЫЙ ПРОЦЕССЫ. ЦИКЛЫ. Эффективность холодильной машины Термический коэффициент характеризует холодильный полезного действия для кругового коэффициент η′ — отношение отнятой от процесса — это величина, равная термостата с более низкой температурой отношению работы, совершенной количества теплоты Q 2 к работе A, которая системой, к количеству теплоты, затрачивается на полученному в этом цикле систем приведение холодильной машины в действие: Цикл называется прямым, если за цикл совершается положительная работа (A) Цикл называется обратным, если за цикл совершается отрицательная работа (Б). Обратный цикл используется в холодильных машинах (за счет работы внешних сил теплота переносится к телу с более высокой температурой).
ОБРАТИМЫЙ И НЕОБРАТИМЫЙ ПРОЦЕССЫ. ЦИКЛЫ. Эффективность холодильной машины Термический коэффициент характеризует холодильный полезного действия для кругового коэффициент η′ — отношение отнятой от процесса — это величина, равная термостата с более низкой температурой отношению работы, совершенной количества теплоты Q 2 к работе A, которая системой, к количеству теплоты, затрачивается на полученному в этом цикле систем приведение холодильной машины в действие: Цикл называется прямым, если за цикл совершается положительная работа (A) Цикл называется обратным, если за цикл совершается отрицательная работа (Б). Обратный цикл используется в холодильных машинах (за счет работы внешних сил теплота переносится к телу с более высокой температурой).
 ТЕОРЕМА КАРНО. ЦИКЛ КАРНО Наиболее экономичный обратимый круговой процесс, состоящий из двух изотерм и двух адиабат. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем. Теорема Карно КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны другу и не зависят от природы рабочего тела, а определяются только температурами нагревателя и холодильника Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей T 1 и холодильников T 2, наибольшим КПД обладают обратимые машины
ТЕОРЕМА КАРНО. ЦИКЛ КАРНО Наиболее экономичный обратимый круговой процесс, состоящий из двух изотерм и двух адиабат. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем. Теорема Карно КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны другу и не зависят от природы рабочего тела, а определяются только температурами нагревателя и холодильника Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей T 1 и холодильников T 2, наибольшим КПД обладают обратимые машины
 ТЕОРЕМА КАРНО. ЦИКЛ КАРНО Адиабатическое расширение Изотермическое сжатие Адиабатическое сжатие Изотермическое расширение
ТЕОРЕМА КАРНО. ЦИКЛ КАРНО Адиабатическое расширение Изотермическое сжатие Адиабатическое сжатие Изотермическое расширение
 ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ. Первое начало термодинамики выражает закон сохранения и превращения энергии применительно к термодинамическим процессам. Второе начало термодинамики определяет направление протекания термодинамических процессов, указывая, какие процессы в природе возможны, а какие — нет. Второй закон указывает на неравноценность двух форм передачи энергии – работы и теплоты. Внутренняя энергия в работу может быть переведена посредством дополнительных процессов (передача тепла холодильнику) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к телу более нагретому. по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; Механическая энергия переходит в тепло без каких либо дополнительных процессов
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ. Первое начало термодинамики выражает закон сохранения и превращения энергии применительно к термодинамическим процессам. Второе начало термодинамики определяет направление протекания термодинамических процессов, указывая, какие процессы в природе возможны, а какие — нет. Второй закон указывает на неравноценность двух форм передачи энергии – работы и теплоты. Внутренняя энергия в работу может быть переведена посредством дополнительных процессов (передача тепла холодильнику) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к телу более нагретому. по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; Механическая энергия переходит в тепло без каких либо дополнительных процессов
 ЭНТРОПИЯ приведенное количество теплоты — отношение теплоты δQ к температуре T системы при бесконечно малых изменениях состояния системы — есть функция состояния системы. Энтропией S называется функция состояния системы, дифференциалом которой является δQ /T Любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает (закон возрастания энтропии). энтропии
ЭНТРОПИЯ приведенное количество теплоты — отношение теплоты δQ к температуре T системы при бесконечно малых изменениях состояния системы — есть функция состояния системы. Энтропией S называется функция состояния системы, дифференциалом которой является δQ /T Любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает (закон возрастания энтропии). энтропии
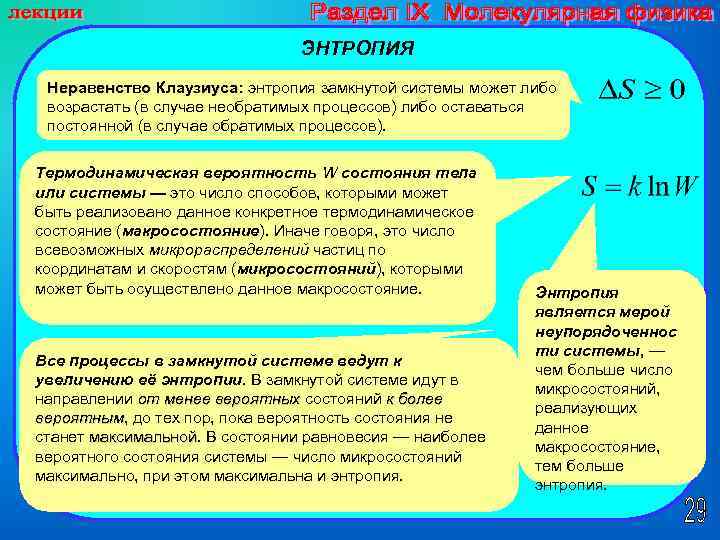 ЭНТРОПИЯ Неравенство Клаузиуса: энтропия замкнутой системы может либо возрастать (в случае необратимых процессов) либо оставаться постоянной (в случае обратимых процессов). Термодинамическая вероятность W состояния тела или системы — это число способов, которыми может быть реализовано данное конкретное термодинамическое состояние (макросостояние). Иначе говоря, это число всевозможных микрораспределений частиц по координатам и скоростям (микросостояний), которыми может быть осуществлено данное макросостояние. Все процессы в замкнутой системе ведут к увеличению её энтропии. В замкнутой системе идут в направлении от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не вероятным станет максимальной. В состоянии равновесия — наиболее максимальной вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия. Энтропия является мерой неупорядоченнос ти системы, — чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия.
ЭНТРОПИЯ Неравенство Клаузиуса: энтропия замкнутой системы может либо возрастать (в случае необратимых процессов) либо оставаться постоянной (в случае обратимых процессов). Термодинамическая вероятность W состояния тела или системы — это число способов, которыми может быть реализовано данное конкретное термодинамическое состояние (макросостояние). Иначе говоря, это число всевозможных микрораспределений частиц по координатам и скоростям (микросостояний), которыми может быть осуществлено данное макросостояние. Все процессы в замкнутой системе ведут к увеличению её энтропии. В замкнутой системе идут в направлении от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не вероятным станет максимальной. В состоянии равновесия — наиболее максимальной вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия. Энтропия является мерой неупорядоченнос ти системы, — чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия.
 ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ Третье начало термодинамики — теорема Нернста– Планка — постулирует поведение термодинамических систем при нуле Кельвина (абсолютном нуле): энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина. Теплоемкость стремиться к нулю быстрее чем линейная функция T – т. е. за конечное число циклов холодильной машины абсолютного нуля достичь невозможно.
ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ Третье начало термодинамики — теорема Нернста– Планка — постулирует поведение термодинамических систем при нуле Кельвина (абсолютном нуле): энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина. Теплоемкость стремиться к нулю быстрее чем линейная функция T – т. е. за конечное число циклов холодильной машины абсолютного нуля достичь невозможно.
 ЭНТРОПИЯ В ИЗОПРОЦЕССАХ.
ЭНТРОПИЯ В ИЗОПРОЦЕССАХ.
 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ РАВНОВЕСНОГО СОСТОЯНИЯ СИСТЕМЫ. Закрытая система N=const Открытая система N≠const Химический потенциал системы Энтальпия (теплосодержание)
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ РАВНОВЕСНОГО СОСТОЯНИЯ СИСТЕМЫ. Закрытая система N=const Открытая система N≠const Химический потенциал системы Энтальпия (теплосодержание)
 ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ РАВНОВЕСНОГО СОСТОЯНИЯ СИСТЕМЫ. Потенциал Гиббса (Изобарно -изотермический потенциал) Свободная энергия Гельмгольца (Изохорно-изотермический потенциал)
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ РАВНОВЕСНОГО СОСТОЯНИЯ СИСТЕМЫ. Потенциал Гиббса (Изобарно -изотермический потенциал) Свободная энергия Гельмгольца (Изохорно-изотермический потенциал)
 ЗАКОН БОЛЬЦМАНА О РАВНОМЕРНОМ РАСПРЕДЕЛЕНИИ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ (ЗАКОН РАВНОРАСПРЕДЕЛЕНИЯ). Для системы, находящейся в состоянии термодинамического равновесия на каждую Число независимых поступательную задающих параметров, и вращательную степень свободы приходится в среднем состояние системы кинетическая энергия, равная k. T/2 , а на каждую колебательную степень свободы — в среднем энергия, равная k. T.
ЗАКОН БОЛЬЦМАНА О РАВНОМЕРНОМ РАСПРЕДЕЛЕНИИ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ (ЗАКОН РАВНОРАСПРЕДЕЛЕНИЯ). Для системы, находящейся в состоянии термодинамического равновесия на каждую Число независимых поступательную задающих параметров, и вращательную степень свободы приходится в среднем состояние системы кинетическая энергия, равная k. T/2 , а на каждую колебательную степень свободы — в среднем энергия, равная k. T.
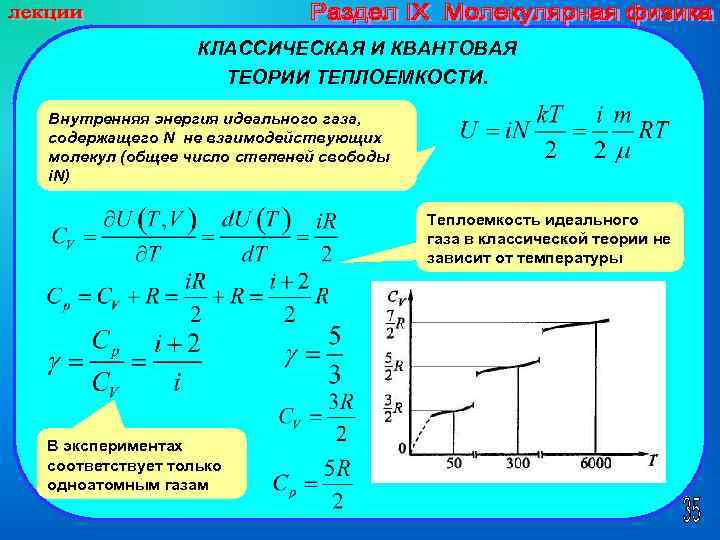 КЛАССИЧЕСКАЯ И КВАНТОВАЯ ТЕОРИИ ТЕПЛОЕМКОСТИ. Внутренняя энергия идеального газа, содержащего N не взаимодействующих молекул (общее число степеней свободы i. N) Теплоемкость идеального газа в классической теории не зависит от температуры В экспериментах соответствует только одноатомным газам
КЛАССИЧЕСКАЯ И КВАНТОВАЯ ТЕОРИИ ТЕПЛОЕМКОСТИ. Внутренняя энергия идеального газа, содержащего N не взаимодействующих молекул (общее число степеней свободы i. N) Теплоемкость идеального газа в классической теории не зависит от температуры В экспериментах соответствует только одноатомным газам
 КЛАССИЧЕСКАЯ И КВАНТОВАЯ ТЕОРИИ ТЕПЛОЕМКОСТИ. Спектр энергии квантовомеханического осциллятора При низких температурах вращательные и колебательные уровни возбуждаться не могут Тепловая энергия сравнима с квантом колебательной энергии Спектр энергии квантовомеханического ротатора Тепловая энергия сравнима с квантом вращательной энергии
КЛАССИЧЕСКАЯ И КВАНТОВАЯ ТЕОРИИ ТЕПЛОЕМКОСТИ. Спектр энергии квантовомеханического осциллятора При низких температурах вращательные и колебательные уровни возбуждаться не могут Тепловая энергия сравнима с квантом колебательной энергии Спектр энергии квантовомеханического ротатора Тепловая энергия сравнима с квантом вращательной энергии
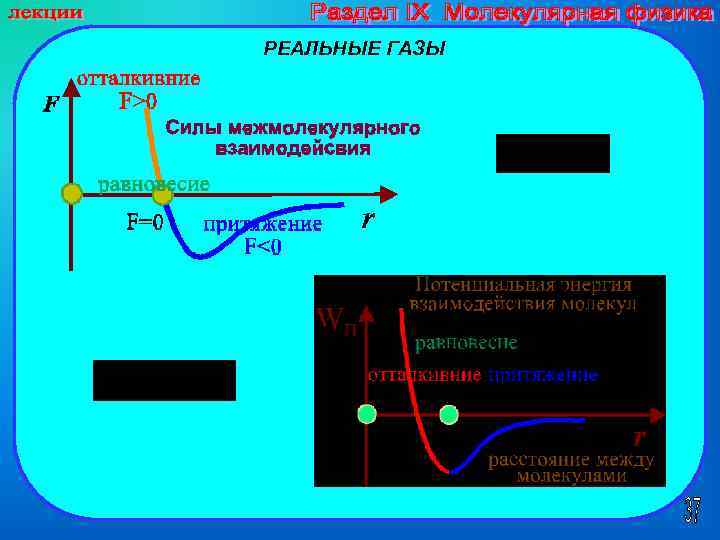 РЕАЛЬНЫЕ ГАЗЫ
РЕАЛЬНЫЕ ГАЗЫ
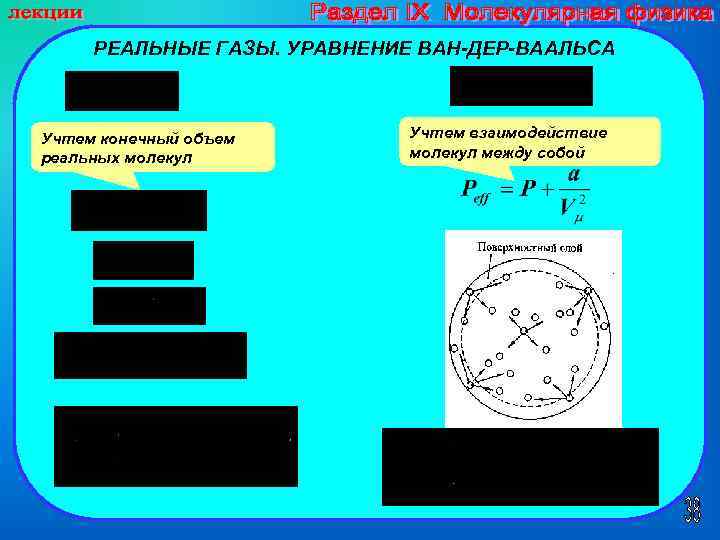 РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА Учтем конечный объем реальных молекул Учтем взаимодействие молекул между собой
РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА Учтем конечный объем реальных молекул Учтем взаимодействие молекул между собой
 РЕАЛЬНЫЕ ГАЗЫ. ВНУТРЕННЯЯ ЭНЕРГИЯ. ЭНТРОПИЯ Внутренняя энергия энтропия
РЕАЛЬНЫЕ ГАЗЫ. ВНУТРЕННЯЯ ЭНЕРГИЯ. ЭНТРОПИЯ Внутренняя энергия энтропия
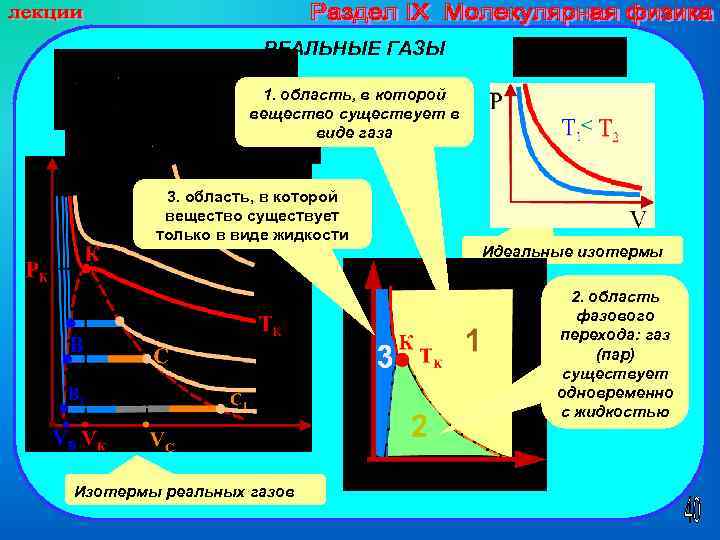 РЕАЛЬНЫЕ ГАЗЫ 1. область, в которой вещество существует в виде газа 3. область, в которой вещество существует только в виде жидкости Идеальные изотермы 2. область фазового перехода: газ (пар) существует одновременно с жидкостью Изотермы реальных газов
РЕАЛЬНЫЕ ГАЗЫ 1. область, в которой вещество существует в виде газа 3. область, в которой вещество существует только в виде жидкости Идеальные изотермы 2. область фазового перехода: газ (пар) существует одновременно с жидкостью Изотермы реальных газов
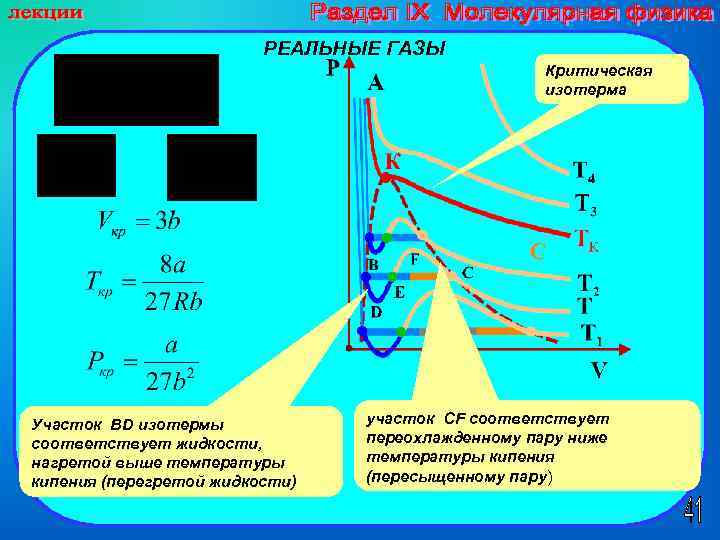 РЕАЛЬНЫЕ ГАЗЫ Критическая изотерма Участок BD изотермы соответствует жидкости, нагретой выше температуры кипения (перегретой жидкости) участок СF соответствует переохлажденному пару ниже температуры кипения (пересыщенному пару)
РЕАЛЬНЫЕ ГАЗЫ Критическая изотерма Участок BD изотермы соответствует жидкости, нагретой выше температуры кипения (перегретой жидкости) участок СF соответствует переохлажденному пару ниже температуры кипения (пересыщенному пару)
 РЕАЛЬНЫЕ ГАЗЫ. ЭФФЕКТ ДЖОУЛЯ-ТОМСОНА Изменение температуры реального газа при течении газа через пробку из сосуда с адиабатическими стенками 1. Энтальпия в процессе Джоуля-Томсона сохраняется 2. Для идеального газа эффекта Джоуля Томсона не наблюдается 3. Для реальных газов эффект Джоуля Томсона может быть как положительным (газ охлаждается) так и отрицательным (газ нагревается)
РЕАЛЬНЫЕ ГАЗЫ. ЭФФЕКТ ДЖОУЛЯ-ТОМСОНА Изменение температуры реального газа при течении газа через пробку из сосуда с адиабатическими стенками 1. Энтальпия в процессе Джоуля-Томсона сохраняется 2. Для идеального газа эффекта Джоуля Томсона не наблюдается 3. Для реальных газов эффект Джоуля Томсона может быть как положительным (газ охлаждается) так и отрицательным (газ нагревается)
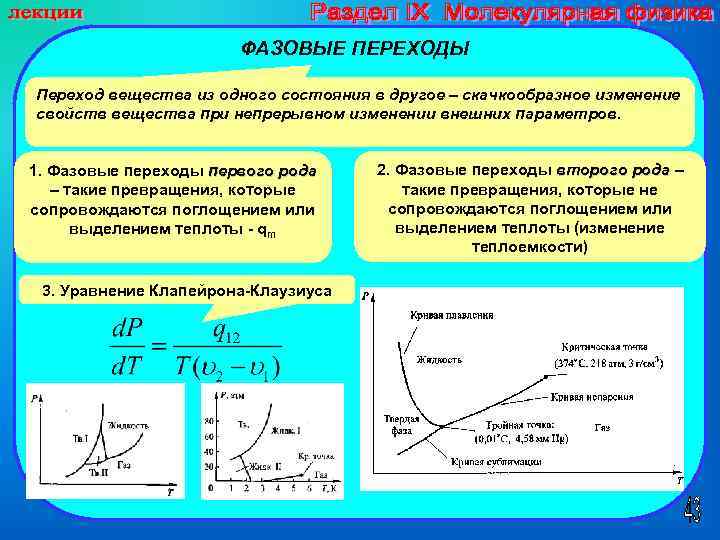 ФАЗОВЫЕ ПЕРЕХОДЫ Переход вещества из одного состояния в другое – скачкообразное изменение свойств вещества при непрерывном изменении внешних параметров. 1. Фазовые переходы первого рода – такие превращения, которые сопровождаются поглощением или выделением теплоты - qm 3. Уравнение Клапейрона-Клаузиуса 2. Фазовые переходы второго рода – такие превращения, которые не сопровождаются поглощением или выделением теплоты (изменение теплоемкости)
ФАЗОВЫЕ ПЕРЕХОДЫ Переход вещества из одного состояния в другое – скачкообразное изменение свойств вещества при непрерывном изменении внешних параметров. 1. Фазовые переходы первого рода – такие превращения, которые сопровождаются поглощением или выделением теплоты - qm 3. Уравнение Клапейрона-Клаузиуса 2. Фазовые переходы второго рода – такие превращения, которые не сопровождаются поглощением или выделением теплоты (изменение теплоемкости)
 Вопросы, выносимые на 3 -ий коллоквиум 1. 2. 3. Идеальный газ. Основные понятия. Уравнение состояния. Распределение Максвелла и Больцмана. Средние значения. Распределение энергии по степеням свободы. Классическая и квантовая теории теплопроводности. 4. Поток частиц и энергии на стенку. 5. Явления переноса. 6. Первое начало термодинамики. Внутренняя энергия. Теплоемкость. Уравнение Майера. 7. Изопроцессы. Первое начало в применении к изопроцессам. 8. Адиабатный процесс. Уравнения Пуассона. 9. Теплоемкость. Политропические процессы. 10. Циклы. Тепловые и холодильные машины. КПД. Цикл Карно. Теорема Карно. 11. Энтропия. II и III начала термодинамики. Энтропия в изопроцессах. 12. Термодинамические функции состояния. 13. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реального газа. 14. Реальные газы. Внутренняя энергия реального газа. Энтропия. Эффект Джоуля-Томсона. 15. Фазовые переходы. Критические значения. Уравнение Клаузиуса. Клапейрона.
Вопросы, выносимые на 3 -ий коллоквиум 1. 2. 3. Идеальный газ. Основные понятия. Уравнение состояния. Распределение Максвелла и Больцмана. Средние значения. Распределение энергии по степеням свободы. Классическая и квантовая теории теплопроводности. 4. Поток частиц и энергии на стенку. 5. Явления переноса. 6. Первое начало термодинамики. Внутренняя энергия. Теплоемкость. Уравнение Майера. 7. Изопроцессы. Первое начало в применении к изопроцессам. 8. Адиабатный процесс. Уравнения Пуассона. 9. Теплоемкость. Политропические процессы. 10. Циклы. Тепловые и холодильные машины. КПД. Цикл Карно. Теорема Карно. 11. Энтропия. II и III начала термодинамики. Энтропия в изопроцессах. 12. Термодинамические функции состояния. 13. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реального газа. 14. Реальные газы. Внутренняя энергия реального газа. Энтропия. Эффект Джоуля-Томсона. 15. Фазовые переходы. Критические значения. Уравнение Клаузиуса. Клапейрона.
 Задания по вариантам 1. Определить удельную теплоемкость cp смеси кислорода и азота, если количество вещества 1 первого компонента равно 2 молям, а количество вещества 2 второго равно 4 молям. 2. Кислород, занимавший объем V 1 = 1 л под давлением р1 = 1, 2 МПа, адиабатически расширился до объема V 2 = 10 л. Определить работу А расширения газа. 3. Разность удельных теплоемкостей cp – c. V некоторого двухатомного газа равна 260 Дж/(кг К). Найти молярную массу газа и его удельные теплоемкости c. V и cp. 4. При адиабатическом расширении кислорода с начальной температурой Т 1 = 320 К внутренняя энергия уменьшилась на U = 8, 4 к. Дж, а его объем увеличился в 10 раз. Определить массу кислорода. 5. Баллон объемом 20 л содержит водород при температуре 300 К под давлением 0, 4 МПа. Каковы будут температура и давление, если газу сообщить количество теплоты Q = 6 к. Дж?
Задания по вариантам 1. Определить удельную теплоемкость cp смеси кислорода и азота, если количество вещества 1 первого компонента равно 2 молям, а количество вещества 2 второго равно 4 молям. 2. Кислород, занимавший объем V 1 = 1 л под давлением р1 = 1, 2 МПа, адиабатически расширился до объема V 2 = 10 л. Определить работу А расширения газа. 3. Разность удельных теплоемкостей cp – c. V некоторого двухатомного газа равна 260 Дж/(кг К). Найти молярную массу газа и его удельные теплоемкости c. V и cp. 4. При адиабатическом расширении кислорода с начальной температурой Т 1 = 320 К внутренняя энергия уменьшилась на U = 8, 4 к. Дж, а его объем увеличился в 10 раз. Определить массу кислорода. 5. Баллон объемом 20 л содержит водород при температуре 300 К под давлением 0, 4 МПа. Каковы будут температура и давление, если газу сообщить количество теплоты Q = 6 к. Дж?
 Задания по вариантам 6. Гелий массой 1 г был нагрет на Т = 100 К при постоянном давлении р. Определить: 1) количество теплоты Q, переданное газу; 2) работу А расширения; 3) приращение U внутренней энергии газа. 7. Какая доля 1 количества теплоты, подводимого к многоатомному идеальному газу при изобарическом процессе, расходуется на увеличение его внутренней энергии и какая доля 2 – на работу расширения? Молекулы газа считать жесткими. 8. Азот, занимавший объем V 1 = 10 л под давлением р1 = 0, 2 МПа, изотермически расширился до объема V 2 = 28 л. Определить работу А расширения газа. 9. Нагревается или охлаждается 1 моль идеального газа, если он расширяется по закону p. V 2 = const? Определить молярную теплоемкость газа при этом процессе. 10. Найти кпд цикла, состоящего из двух изохор и двух изобар. Известно, что в пределах цикла максимальные значения объема и давления газа в два раза больше минимальных значений. Газ считать двухатомным, идеальным.
Задания по вариантам 6. Гелий массой 1 г был нагрет на Т = 100 К при постоянном давлении р. Определить: 1) количество теплоты Q, переданное газу; 2) работу А расширения; 3) приращение U внутренней энергии газа. 7. Какая доля 1 количества теплоты, подводимого к многоатомному идеальному газу при изобарическом процессе, расходуется на увеличение его внутренней энергии и какая доля 2 – на работу расширения? Молекулы газа считать жесткими. 8. Азот, занимавший объем V 1 = 10 л под давлением р1 = 0, 2 МПа, изотермически расширился до объема V 2 = 28 л. Определить работу А расширения газа. 9. Нагревается или охлаждается 1 моль идеального газа, если он расширяется по закону p. V 2 = const? Определить молярную теплоемкость газа при этом процессе. 10. Найти кпд цикла, состоящего из двух изохор и двух изобар. Известно, что в пределах цикла максимальные значения объема и давления газа в два раза больше минимальных значений. Газ считать двухатомным, идеальным.


