Молекулярная физика 9 1 Среднее число столкновений

Молекулярная физика 9

1. Среднее число столкновений и средняя длина свободного пробега молекул 2. Распределение молекул по длинам их свободного пробега 3. Эффективное поперечное сечение частицы и вероятность

Диффузия • Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно -кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте.

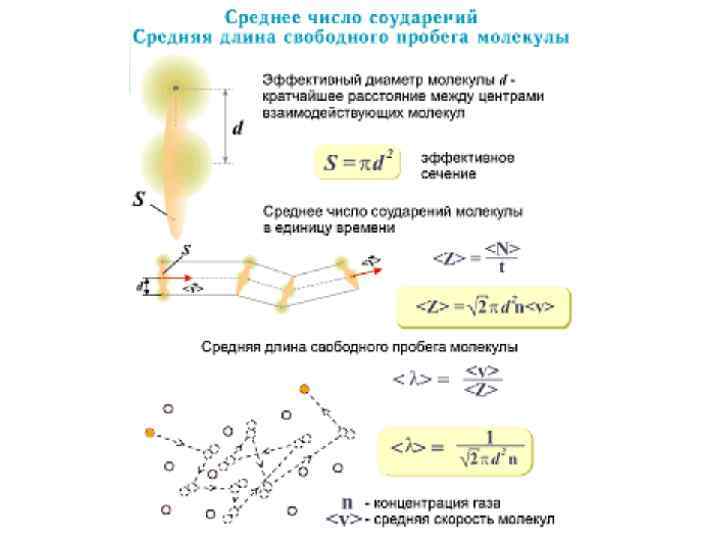
• Известно, что Вывод: чтобы объяснить диффузию, надо предположить, что молекулы сталкиваются Отсюда вопросы: 1) - среднее число столкновений в единицу времени 2) <λ> - средняя длина свободного пробега молекул

Средняя длина свободного пробега молекул • Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. • Между двумя последовательными столкновениями молекулы проходят некоторый путь λ, который называется длиной свободного пробега. • В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул < λ >. • Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. ). • Он зависит от скорости сталкивающихся молекул т. е. от температуры газа (несколько уменьшается с ростом температуры).

Среднее число столкновений • Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости , ( ), и если среднее число столкновений, испытываемых одной молекулой газа за 1 с, то средняя длина свободного пробега • Для определения представим себе молекулу в виде шарика диаметром d, которая движется среди других «покоящихся» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри «ломаного» цилиндра радиусом d (рис. ). d σ=πd 2 t

Среднее число столкновений d σ=πd 2 t • Среднее число столкновений за 1 с равно числу молекул в объеме «ломаного» цилиндра: • где п — концентрация молекул, • средняя скорость молекулы или путь, пройденный ею за 1 с). Таким образом, среднее число столкновений •

Среднее число столкновений Средняя длина свободного пробега молекул • Расчеты показывают, что при учете движения других молекул • Тогда средняя длина свободного пробега • т. е. <λ> обратно пропорциональна концентрации п молекул. С другой стороны, из p=nk. T следует, что при постоянной температуре п пропорциональна давлению р. Следовательно, • <λ>~1/p : p – мало → λ – велико, при <λ> >>> L имеем вакуум • Например для азота при н. у. <λ>~10 -7 м

Распределение молекул по длинам их свободного пробега • Надо найти • Из распределения Максвелла • Запишем это распределение в новых переменных • Учтем, что и подставим

Распределение молекул по длинам их свободного пробега Теперь имеем Эта величина представляет самостоятельный интерес , например в кинетике, химии. Кроме того позволяет решать задачи аналогично распределению Максвелла. Например

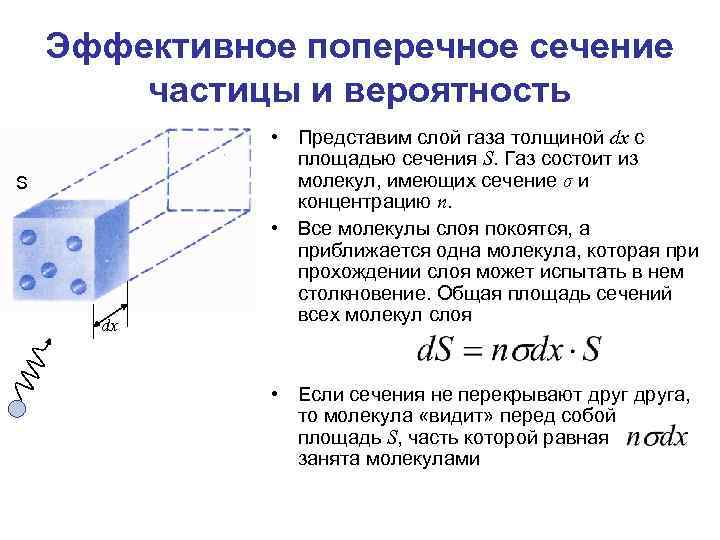Эффективное поперечное сечение частицы и вероятность S dx • Представим слой газа толщиной dx с площадью сечения S. Газ состоит из молекул, имеющих сечение σ и концентрацию n. • Все молекулы слоя покоятся, а приближается одна молекула, которая при прохождении слоя может испытать в нем столкновение. Общая площадь сечений всех молекул слоя • Если сечения не перекрывают друга, то молекула «видит» перед собой площадь S, часть которой равная занята молекулами

Эффективное поперечное сечение частицы и вероятность • Если бы вся площадь S была перекрыта сечениями, то вероятность столкновения была бы равна 1. • Чем большая часть перекрыта, тем больше вероятность столкновения S dx Специальная единица измерения – Барн. Соизмерима с размерами атомов. • - вероятность того, что молекула испытает столкновение на пути dx в газе. • Эффективное поперечное сечение молекул σ связано с вероятностью столкновения (рассеяния) молекул и не имеет чисто геометрического смысла. • Если эффективное поперечное сечение велико, то это не означает, что молекула «большая» , а означает, что вероятность столкновения велика.

Барн • Барн (сокращение: б, бн) — в ядерной физике единица для измерения эффективного поперечного сечения ядерных реакций. Имеет размерность площади, 1 барн численно равен 10− 28 м² = 10− 24 cм². Определяются также дольные единицы (миллибарн, микробарн, нанобарн и т. д. )

Этимология • Название «барн» происходит от английского barn — амбар. Два физика из Университета Пердью (Уэст. Лафаетт, штат Индиана), Маршалл Хеллоуэй и Чарльз Бэйкер, работавшие в рамках Манхэттенского проекта, однажды во время обеда решили придумать название для единицы, отражающей типичный размер эффективного сечения в ядерной физике. Среди кандидатов, в чью она честь могла быть названа, были Оппенгеймер и Бете, а также Джон Мэнли, директор группы университета Пердью в Лос. Аламосе (Мэнли показалось физикам слишком длинным, и в качестве кандидатуры некоторое время использовалось имя «Джон» ). Для большинства ядерных процессов эффективное сечение 10− 24 см² кажется большим, как амбар.

Эффективное поперечное сечение частицы и вероятность • Следующая механическая аналогия поможет уяснить себе рассматриваемую молекулярную ситуацию. Представим себе забор из досок, разделенных свободными промежутками. Недалеко от забора человек кидает их (не прицеливаясь) по направлению к забору, так что камешки приблизительно равномерно распределяются по выделенному участку ограды. Очевидно, что некоторые из брошенных камней пройдут через промежутки между досками, другие попадут в доски. По израсходовании запаса камней (если он был достаточно велик) можно убедиться в том, что отношение числа камней, прошедших сквозь ограду, к общему числу брошенных камней приблизительно равно отношению площади промежутков в выбранном участке ограды к общей его площади. • Первое из этих отношений есть отношение числа опытов, приводящих к осуществлению некоторого события (прохождения камня сквозь ограду), к общему числу опытов. По принятому нами определению оно равно вероятности события. Значит, отношение площадей промежутков к площади всей ограды как раз равно этой вероятности.

Эффективное поперечное сечение частицы и вероятность • Обращаясь снова к случаю встречи летящей молекулы со слоем газа, мы можем и здесь сказать, что каждая молекула, летящая к слою, может испытать в нем столкновение, но может и пройти через него, не столкнувшись ни с одной из его молекул. Но если подобный опыт повторять достаточно много раз, то ясно, что отношение числа случаев, когда исходом опыта будет столкновение, к общему числу опытов будет равно отношению площади сечений всех молекул слоя к площади слоя.

Эффективное поперечное сечение частицы и вероятность • Понятно поэтому, что эффективный поперечник даже у одних и тех же частиц в разных условиях и для различных процессов может быть различным. Это было бы непонятно, если эффективное поперечное сечение действительно было бы просто геометрической площадью сечения молекулы, рассматриваемой как твердый шарик.

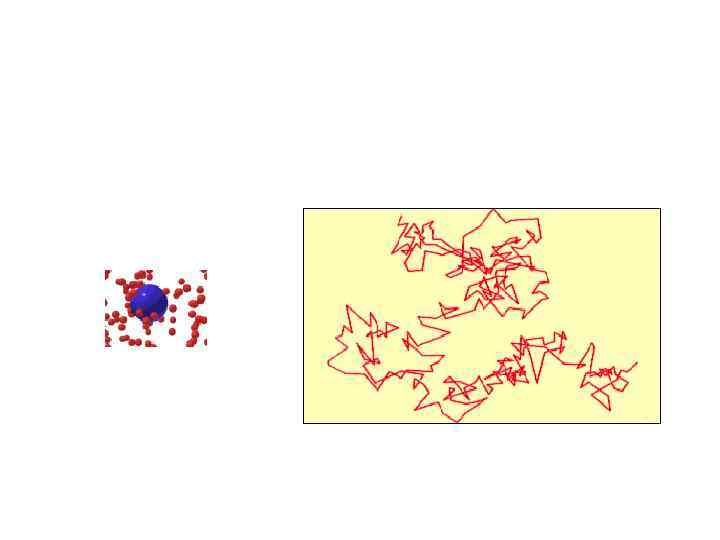
• • • Всем известно, что в отсутствии конвекционных потоков запах в воздухе распространяется очень медленно, в то время как скорость молекул газа достаточно высока (около 500 метров в секунду). Причина этого заключается в том , что распространение запаха осуществляется посредством медленного процесса диффузии. Медленность диффузии и аналогичных ей явлений Клаузиус объяснил столкновениями молекул. Молекула газа не всё время движется свободно, а время от времени испытывает столкновения с другими молекулами. Свободно она пролетает короткое расстояние от одного столкновения до следующего. В результате траектория молекулы описывается ломаной линией с большим количеством звеньев. Для количественного описания явления Клаузиус ввёл понятие средней длины свободного пробега, т. е. среднего расстояния, которое пролетает молекула от одного столкновения до следующего. Этот параметр имеет важное значение для описание явлений переноса - диффузии, внутреннего трения и теплопроводности. Найдём значение средней длины свободного пробега L для газа, состоящего из одинаковых молекул диаметром d. Молекулы будут сталкиваться друг с другом если расстояние между их центрами меньше d. Поэтому, мы можем рассмотреть одну молекулу с радиусом d, движущуюся в присутствии точечных частиц (см. анимацию). В течение времени t эта молекула столкнется со всеми частицами, лежащими внутри цилиндра объёмом (πd 2)nvt, где n - концентрация молекул газа, v - средняя скорость их движения. Средняя длина свободного пробега равняется высоте цилиндра L=vt, который содержит в среднем лишь одну молекулу: L =1/(πd 2 n) Строгий расчёт средней длины свободного пробега был дан Максвеллом с учётом распределения молекул по скоростям. Максвелл получил: L =0. 707/(πd 2 n) Мы можем видеть, что результаты приближённой теории отличаются от точной формулы лишь численными коэффициентами, близкими к единице.