7а - Средние скорости молекул.ppt
- Количество слайдов: 16

Молекулярная физика 7 б

1. Средние скорости молекул. 2. Средняя арифметическая скорость 3. Средняя квадратичная скорость молекул 4. Наивероятнейшая скорость молекул

Средняя арифметическая скорость • Пользуясь функцией распределения Максвелла, можно вычислить ряд величин, важных для молекулярной физики. В качестве примеров мы приведем вычисления средней арифметической скорости , средней квадратичной скорости и наивероятнейшей скорости. Начнем со средней арифметической скорости молекул. • Средняя арифметическая скорость по определению равна отношению суммы всех скоростей всех молекул в единице объема к числу молекул в единице объема.

Средняя арифметическая скорость • Число молекул в единице объема, скорости которых заключены в интервале от до , равно, очевидно, . Сумма скоростей всех таких молекул равна. Чтобы найти сумму скоростей всех молекул, обладающих любыми скоростями, нужно эту функцию проинтегрировать по всем возможным скоростям от нуля до бесконечности. Следовательно, сумма всех скоростей равна • а средняя арифметическая скорость равна

Средняя арифметическая скорость • Подставив сюда полученное раньше выражение для • получим: • Чтобы вычислить входящий в это выражение интеграл, преобразуем подинтегральное выражение: • Так как то

Средняя арифметическая скорость • Введя новую переменную получим: • Интегрирование по частям даёт: • Таким образом, для интеграла в формуле получаем выражение: • Находим для выражение:
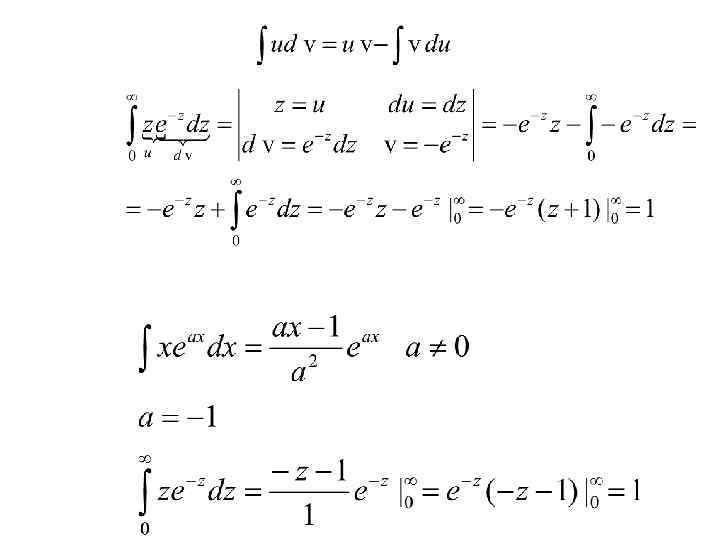

• • Средняя квадратичная скорость молекул Чтобы найти среднюю квадратичную скорость молекул , нужно вычислить отношение суммы квадратов скоростей молекул единицы объема к числу молекул в этом объеме. • Повторяя предыдущие рассуждения, получаем:

Средняя квадратичная скорость • Интеграл, входящий сюда, находим интегрированием по частям и получаем: • Отсюда и • Такое выражение мы получили и раньше.

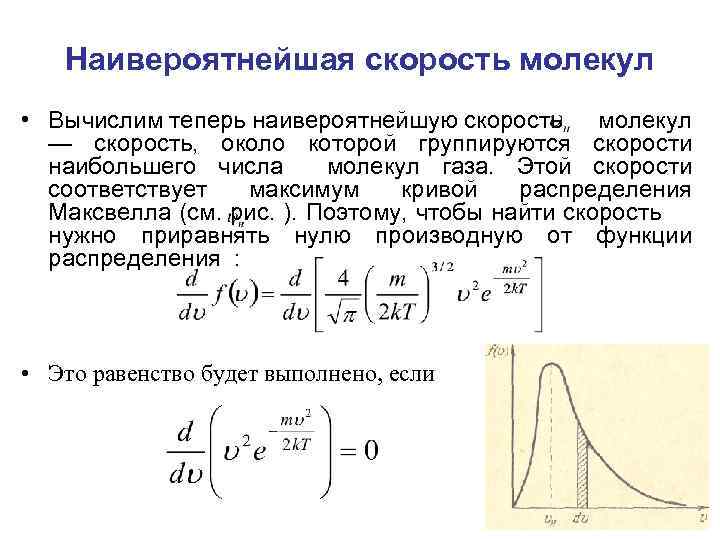
Наивероятнейшая скорость молекул • Вычислим теперь наивероятнейшую скорость молекул — скорость, около которой группируются скорости наибольшего числа молекул газа. Этой скорости соответствует максимум кривой распределения Максвелла (см. рис. ). Поэтому, чтобы найти скорость нужно приравнять нулю производную от функции распределения : • Это равенство будет выполнено, если
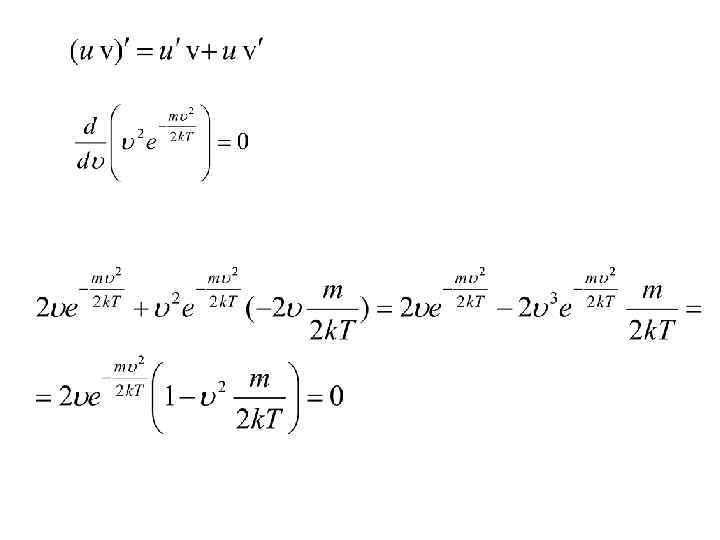

Наивероятнейшая скорость молекул • Проведя дифференцирование, получим: • Это равенство выполняется либо при , либо при • либо при условии, что. Ясно, что первые два условия не соответствуют максимуму кривой распределения.

Наивероятнейшая скорость молекул • Следовательно, значение условия определяется из • Отсюда • Сравнивая полученные выражения, находим соотношение между тремя вычисленными значениями скоростей: • Как видно, различие между этими тремя значениями не очень велико: и средняя арифметическая, и средняя квадратичная скорости близки к наивероятнейшей скорости.


7а - Средние скорости молекул.ppt