Молекулярная физика 1 Понятие о вероятности 2

Молекулярная физика

1. Понятие о вероятности 2. Понятие о распределении. 3. Функция распределения

Понятие о вероятности • Закон Больцмана, как и барометрическую формулу, удобно трактовать с несколько иной точки зрения, а именно, пользуясь понятием вероятности. • К этому термину прибегают в тех случаях, когда речь идет о случайных событиях, т. е. таких, условия наступления которых неизвестны и которые поэтому нельзя заранее с уверенностью предсказать.

Понятие о вероятности • Приобретая, например, билет в автобусе, мы обычно заранее не знаем, будет ли его номер четным или нечетным. Поэтому такое «событие» , как приобретение билета именно с четным номером, можно считать событием случайным. Если мы, например, приобретем 10 билетов, то в их числе могут оказаться и три, и шесть, и восемь билетов с четными номерами. Но может случиться и так, что среди них не окажется ни одного четного, или, наоборот, четными окажутся все 10 билетов. • Однако в этой кажущейся полнейшей произвольности есть и определенная закономерность. Она заключается в том, что, если повторять опыт (покупки билетов) достаточно большое число раз, то приблизительно в половине случаев билет будет иметь четный номер. И чем больше будет число таких «опытов» , тем ближе к половине будет доля билетов с четными номерами. В таком случае и говорят, что вероятность приобретения билета с четным номером равна 1/2. • Точно так же, бросая много раз монету, мы можем быть уверены, что приблизительно в половине случаев она упадет обращенной вверх стороной с гербом. И это будет тем вероятнее, чем больше будет число бросаний.

Понятие о вероятности • Эти и другие подобные им опыты позволяют нам дать следующее определение вероятности: вероятностью события называется предел, к которому стремится отношение числа опытов, приводящих, к его осуществлению, к общему числу опытов при беспредельном увеличении последнего. • Если из N опытов (или наблюдений) N’ приводят к реализации интересующего нас события, то вероятность W этого события выражается формулой:

Понятие о вероятности • В рассмотренном нами случае с номерами билетов вероятность четного номера равна 1/2. Такова же, конечно, и вероятность нечетного номера. Сумма этих двух вероятностей равна единице. Она очевидно дает нам вероятность «события» , заключающегося в том, что билет будет иметь или четный, или нечетный номер. Но такое событие неизбежно, так что вероятность, равная единице, означает достоверность. Наоборот, если какое-то событие невозможно (например, полное отсутствие номера), то его вероятность равна нулю.

Понятие о вероятности • В примере с билетами (так же как и с бросанием монет) «опыт» (покупка билета) может привести к одному из двух исходов: номер билета может быть четным или нечетным, и оба эти исхода являются равновозможными. Но так бывает не всегда. Например, из того факта, что при выстреле в цель возможно лишь два исхода — попадание или промах, не следует, что вероятность попадания равна 1/2, так как попадание и промах не являются равновозможными результатами выстрела. И если будет произведено очень много выстрелов, то отношение числа попаданий к числу выстрелов едва ли будет равно половине: у искусного стрелка, снабженного хорошо пристрелянным оружием, оно будет близким к единице, у плохого оно может мало отличаться от нуля. Однако, хотя вероятности каждого из двух возможных исходов выстрела и не равны 1/2, их сумма (для данного стрелка) и в этом случае равна единице: о том, что выстрел приведет к какому-то исходу — попаданию или промаху, можно утверждать с полной определенностью!

Теорема сложения вероятностей • Рассмотрим теперь еще один пример, который позволит нам сформулировать одно из важных положений теории вероятностей и, кроме того, дать еще одно определение самой величины вероятности. Пусть в ящике лежат 20 вполне одинаковых по своим размерам и весу гладких шаров и пусть 5 из них выкрашены в белый цвет, а остальные — в черный. Если мы теперь извлечем из ящика один шар, то ясно, что, поскольку во всем, кроме цвета, шары друг от друга не отличаются, вероятность вынуть один какой-нибудь шар равна вероятности вынуть любой другой. Для каждого шара, который мы пожелали бы как-нибудь отметить, вероятность быть вынутым равна, очевидно, 1/20. • Посмотрим теперь, какова вероятность того, что будет вынут белый шар? Так как для каждого шара (все равно, белого или черного) вероятность быть вынутым равна 1/20, а всего белых шаров пять (и нам все равно, какой из них будет вынут), то искомая вероятность равна сумме вероятностей для всех белых шаров:

Теорема сложения вероятностей • Этот результат выражает одно из важных положений теории вероятностей — теорему сложения вероятностей, которая гласит: если W 1, W 2, W 3 и т. д. — вероятности нескольких исключающих друга событий, то вероятность того, что осуществится какое-нибудь одно из них, равна сумме вероятностей всех этих событий.

Теорема сложения вероятностей • Вероятность осуществления одного из исключающих друга событий, равна сумме вероятностей всех этих событий.

Понятие о вероятности • Значит, сумма вероятностей нескольких событий дает нам вероятность того, что наступит или одно событие, или другое, или третье и т. д. При этом предполагается, что эти события, или хотя бы два из них, не могут произойти одновременно. Так, в нашем примере 5/20 — это вероятность того, что будет вынут один из белых шаров, а так как операция извлечения шара производится только один раз, то если вынут один какой-нибудь белый шар, то не может быть вынут никакой другой. • Приведенный пример позволяет дать новое определение вероятности, несколько отличающееся от прежнего. Мы нашли, что вероятность того, что будет вынут белый шар, равна 5/20. Но число 20 — это число всех возможных исходов операции извлечения шара, а число 5 — это число случаев (из возможных 20), благоприятствующих наступлению данного события — появлению белого шара. Это и позволяет определить вероятность данного события как отношение числа случаев, благоприятствующих его наступлению, к общему числу возможных случаев, если все случаи равновозможны.

Понятие о вероятности • Это определение вероятности принадлежит Лапласу. Оно, как легко видеть, не противоречит прежнему определению. Для приведенного только что определения вероятности существенно, чтобы все случаи были равновозможны, равновероятны. Именно так обстоит дело в нашем примере с шарами. • При физических применениях теории вероятностей обычно тоже приходится иметь дело с равновероятными событиями.

Понятие о вероятности • Вернемся теперь к формуле закона Больцмана Из того, что здесь было сказано о вероятности, ясно, что величина n/n 0 в этой формуле как раз и имеет смысл вероятности. Ведь любая из n 0 молекул может обладать потенциальной энергией U. Значит, n 0 — это общее число возможных случаев. В действительности же энергией U обладают n молекул. Следовательно, n — это число, которое мы раньше назвали числом «благоприятствующих» случаев. Поэтому отношение n/n 0 , которое мы называли долей молекул, обладающих энергией U, есть в то же время и вероятность того, что любая из n 0 молекул обладает такой энергией.

Теорема умножения вероятностей • Нам остается изложить еще одно важное положение теории вероятностей — теорему умножения вероятностей. Она относится к случаю, когда определяется вероятность сложного события, состоящего в совмещении двух или больше независимых событий. События называются независимыми, если вероятность любого из них не зависит от того, наступит или не наступит любое другое. • Обращаясь к прежним примерам с билетами и стрелком, мы можем, например, поставить такую задачу: какова вероятность того, что стрелок, отправляясь к стрельбищу на автобусе, приобретет билет с четным номером, а вслед затем его первый выстрел увенчается попаданием? Ясно, что эти два события являются независимыми.

Теорема умножения вероятностей • Допустим, что для нашего стрелка вероятность W 1 попадания равна 0, 8. Это значит, что в среднем из 10 посещений стрельбища он в восьми случаях первым выстрелом попадает в цель. Но при этом только в половине из них он приобретет в то же время билет с четным номером, так как вероятность W 2 получить четный билет равна 1/2. Значит, искомая вероятность W 12 сложного события — совпадения четного номера и успешного выстрела — равна произведению вероятностей каждого из них:

Теорема умножения вероятностей • Вероятность совмещения двух или нескольких независимых, событий равна произведению вероятностей каждого из них в отдельности.

Понятие о распределении • В основные уравнения кинетической теории идеальных газов входит, как мы знаем, средняя кинетическая энергия молекул, которая в свою очередь определяется их средней квадратичной скоростью. Смысл средней квадратичной скорости заключается в том, что это — та скорость, которой должны были бы обладать все молекулы (если бы величины их скоростей были одинаковы, а направления равновероятны), чтобы давление газа было тем, каким оно в действительности является. На самом деле, однако, скорости молекул не одинаковы, и мы это даже принимали во внимание при выводе основного уравнения. На это указывают и опытные факты. Так, например, в опытах Штерна, в которых измерялась скорость молекул, смещенная полоска оказывалась не резкой, а размытой изза того, что молекулы с разными скоростями попадали в разные места мишени. Об этом свидетельствует и рассмотренный закон распределения молекул по высоте в поле тяжести (барометрическая формула). Если бы все молекулы имели одинаковые скорости, распределение было бы совсем иным.

Опыт Штерна

Понятие о распределении • В самом деле, представим себе, что все молекулы, находящиеся у поверхности Земли, имеют одинаковые скорости, вертикальная составляющая которых равна и. Эти молекулы поднялись бы до высоты х, определяемой условием • т. е. до высоты • после чего они вернулись бы к Земле с первоначальной кинетической энергией, т. е. они вели бы себя так же, как ведет себя любое брошенное вверх тело. При таких условиях атмосфера имела бы на высоте х резкую границу, за пределами которой ее не было бы. Опыт же показывает, что атмосфера резкой границы не имеет, ее плотность убывает с высотой в соответствии с барометрической формулой. Предположение о равенстве скоростей всех молекул противоречит, таким образом, опыту.

Понятие о распределении • Благодаря беспорядочным движениям молекул и их взаимным столкновениям молекулы газа каким-то образом распределяются по скоростям, так что среди них имеются как очень быстрые, так и очень медленные. • Несмотря на полную хаотичность молекулярных движений, несмотря на случайный характер столкновений и вызываемых ими изменений скорости молекул, их распределение по скоростям, как показывают теория и опыт, оказывается не случайным, не произвольным, а вполне определенным. На его характер не влияют ни столкновения между молекулами, ни даже внешние поля. Оно оказывается однозначным и единственно возможным. И это не только не противоречит представлению о хаотичности молекулярных движений, но именно ею и обусловлено.

Понятие о распределении • Прежде чем приступить к выводу закона распределения молекул по скоростям, выясним сущность задачи о распределении. Определить распределение молекул по скоростям означает, как будто бы, определить число молекул, обладающих той или иной заданной скоростью. Однако в такой постановке вопрос не имеет смысла, так как вероятное число молекул, имеющих точно (математически точно!) заданную скорость, равно нулю. Ведь число различных значений скорости бесконечно большое. Число же молекул конечное. Поэтому число молекул, приходящихся на долю каждого произвольно заданного значения скорости, равно нулю. Вследствие этого вопрос должен быть сформулирован "иначе: сколько молекул (или какая часть молекул) обладает скоростями, лежащими в некотором интервале вблизи заданной скорости?

Понятие о распределении • Именно так всегда и ставятся статистические задачи. Если, например, требуется найти распределение населения страны по возрасту, то это не значит, что нужно определить вероятное число людей, имеющих тот или иной точно (математически точно) заданный возраст. Такой вопрос не имеет смысла, так как число различных значений возраста бесконечно большое, а число людей конечное. Можно лишь определить вероятное число людей, возраст которых лежит в определенном интервале значений. • Когда в повседневной речи мы говорим, что такому-то человеку 18 лет, то мы не хотим этим сказать, что ему ровно 18 лет, 0 дней, 0 минут, 0 секунд. Наше утверждение означает лишь, что его возраст лежит в интервале между 18 и 19 годами. Точно так же, когда, например, Министерство образования, планируя работу школ в учебном году, интересуется числом детей семилетнего возраста, поступающих в школу, то оно интересуется не детьми, которым 1 сентября в 8 часов утра исполнится ровно 7 лет. Его на самом деле интересует число детей, чей возраст лежит между семью и восемью годами.

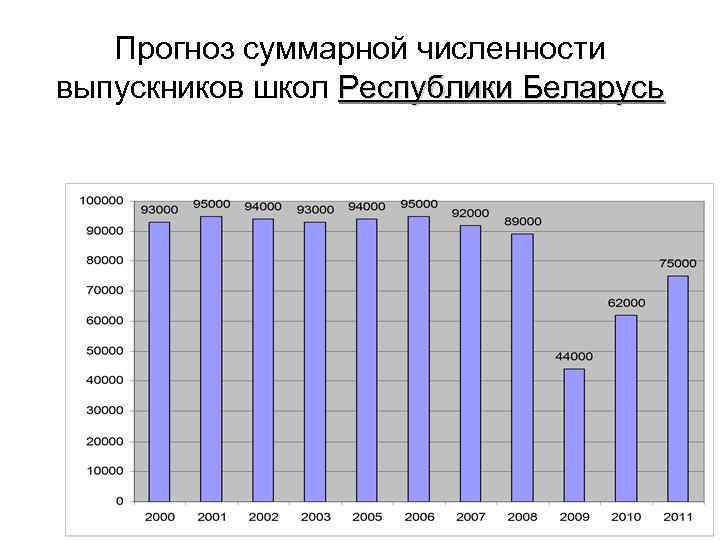Прогноз суммарной численности выпускников школ Республики Беларусь

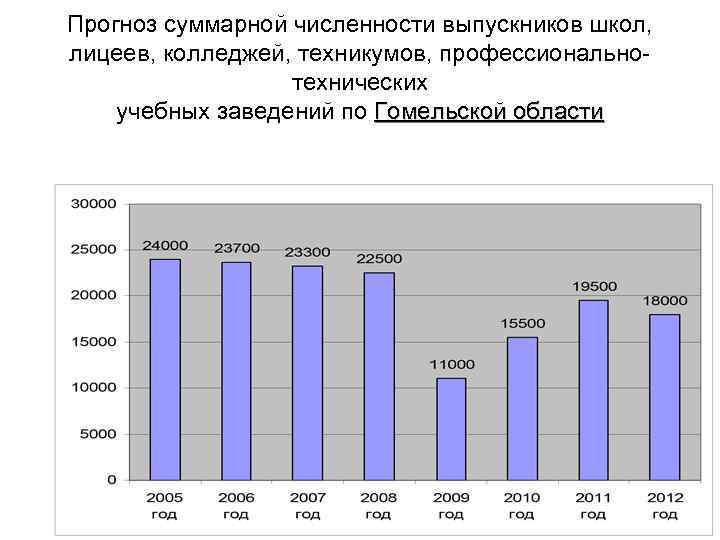Прогноз суммарной численности выпускников школ, лицеев, колледжей, техникумов, профессиональнотехнических учебных заведений по Гомельской области

Функция распределения • Изучая распределение частиц по скоростям, мы тоже будем искать число частиц, скорости которых (или компоненты скорости) лежат в определенном интервале значений скорости (или компонент скорости). • Очевидно, что число частиц в единице объема, скорости которых лежат в некотором интервале от до , тем больше, чем больше интервал, т. е. • или • где а — коэффициент пропорциональности.

Функция распределения • Ясно также, что зависит и от самой скорости, так как в одинаковых по величине интервалах, но при различных абсолютных значениях скорости, число частиц будет различным, как не одинаково, например, число людей в интервале возрастов от 99 до 100 лет и от 30 до 31 года, хотя размеры интервалов в обоих случаях одинаковы. Это значит, что в последней формуле коэффициент пропорциональности должен быть функцией скорости

Функция распределения • Наконец, величина должна быть также пропорциональна числу частиц п в единице объема. Поэтому формула для должна иметь вид: • Ее обычно записывают в таком виде:

Функция распределения • Величина — в этой формуле представляет собой • долю частиц в единице объема газа, скорости которых лежат в интервале от до. • Функция называется функцией распределения. Нашей задачей и является найти вид этой функции. Смысл ее ясен из формулы. В самом деле, • при

Функция распределения • Это значит, что равна доле частиц, скорости которых заключены в единичном интервале скоростей вблизи скорости. • Переходя к пределу, можно формулу переписать в виде:

Функция распределения • Из того, что говорилось выше о вероятности, следует, что • величина в формуле имеет смысл • вероятности: это вероятность того, что любая из молекул газа, содержащихся в единице его объема, обладает скоростью, лежащей в интервале вблизи скорости • . • Величине же функции распределения можно приписать смысл вероятности любой молекуле газа в единице его объема иметь скорость, заключенную в единичном интервале вблизи скорости. Ее называют поэтому плотностью вероятности.

Функция распределения • Полученная ранее барометрическая формула обязана своим видом тому, что скорости молекул не одинаковы, а определенным образом распределены по скоростям. Характер этого распределения как раз и зависит от вида функции. Пользуясь уже известной барометрической формулой, мы и определим вид функции распределения, приводящей к зависимости плотности молекул от высоты:

Функция распределения • Заметим, что функция распределения может быть найдена и другими путями. Максвелл получил ее (1859 г. ) из соображений, основанных на теории вероятностей. Больцман (1877 г. ) вывел эту функцию из рассмотрения столкновений газовых молекул, благодаря которым и устанавливается распределение. Как следствие этой формулы может быть получена и барометрическая формула. Мы же для простоты расчета воспользуемся уже выведенной барометрической формулой, чтобы найти

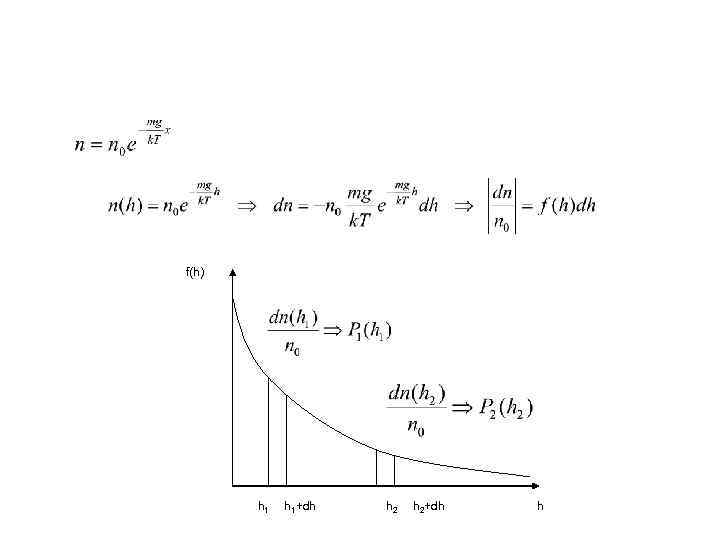f(h) h 1+dh h 2+dh h